問題文全文(内容文):
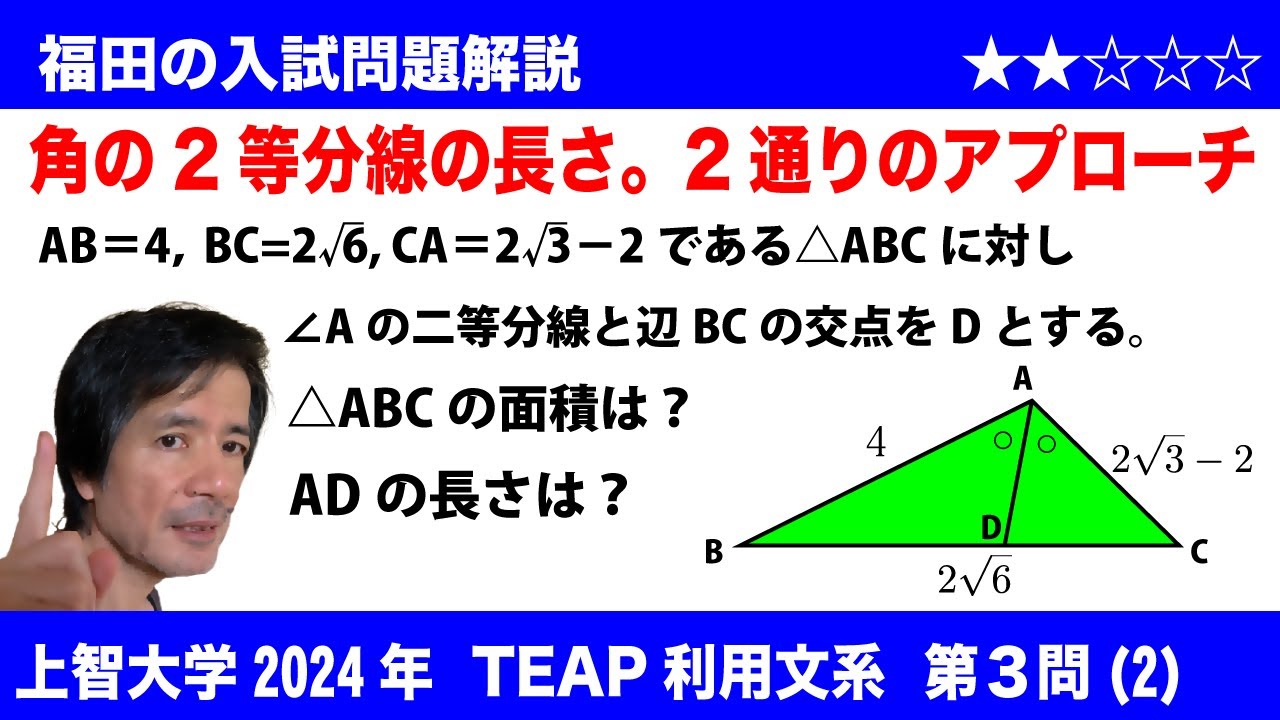
$\Large\boxed{2}$ $|x|$≦2 を満たす複素数$x$と、$|y-(8+6i)|$=3 を満たす複素数$y$に対して、$z$=$\displaystyle\frac{x+y}{2}$ とする。このような複素数$z$が複素数平面において動く領域を図示し、その面積を求めよ。
$\Large\boxed{2}$ $|x|$≦2 を満たす複素数$x$と、$|y-(8+6i)|$=3 を満たす複素数$y$に対して、$z$=$\displaystyle\frac{x+y}{2}$ とする。このような複素数$z$が複素数平面において動く領域を図示し、その面積を求めよ。
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ $|x|$≦2 を満たす複素数$x$と、$|y-(8+6i)|$=3 を満たす複素数$y$に対して、$z$=$\displaystyle\frac{x+y}{2}$ とする。このような複素数$z$が複素数平面において動く領域を図示し、その面積を求めよ。
$\Large\boxed{2}$ $|x|$≦2 を満たす複素数$x$と、$|y-(8+6i)|$=3 を満たす複素数$y$に対して、$z$=$\displaystyle\frac{x+y}{2}$ とする。このような複素数$z$が複素数平面において動く領域を図示し、その面積を求めよ。
投稿日:2024.03.07