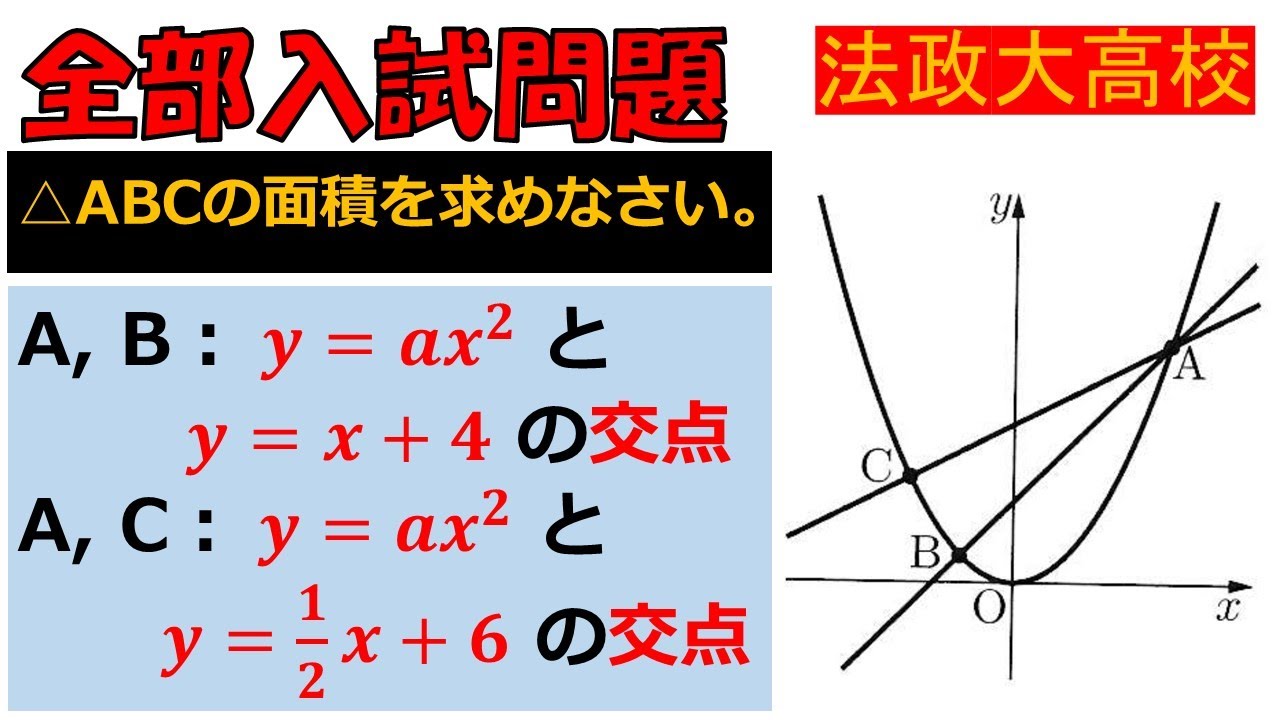
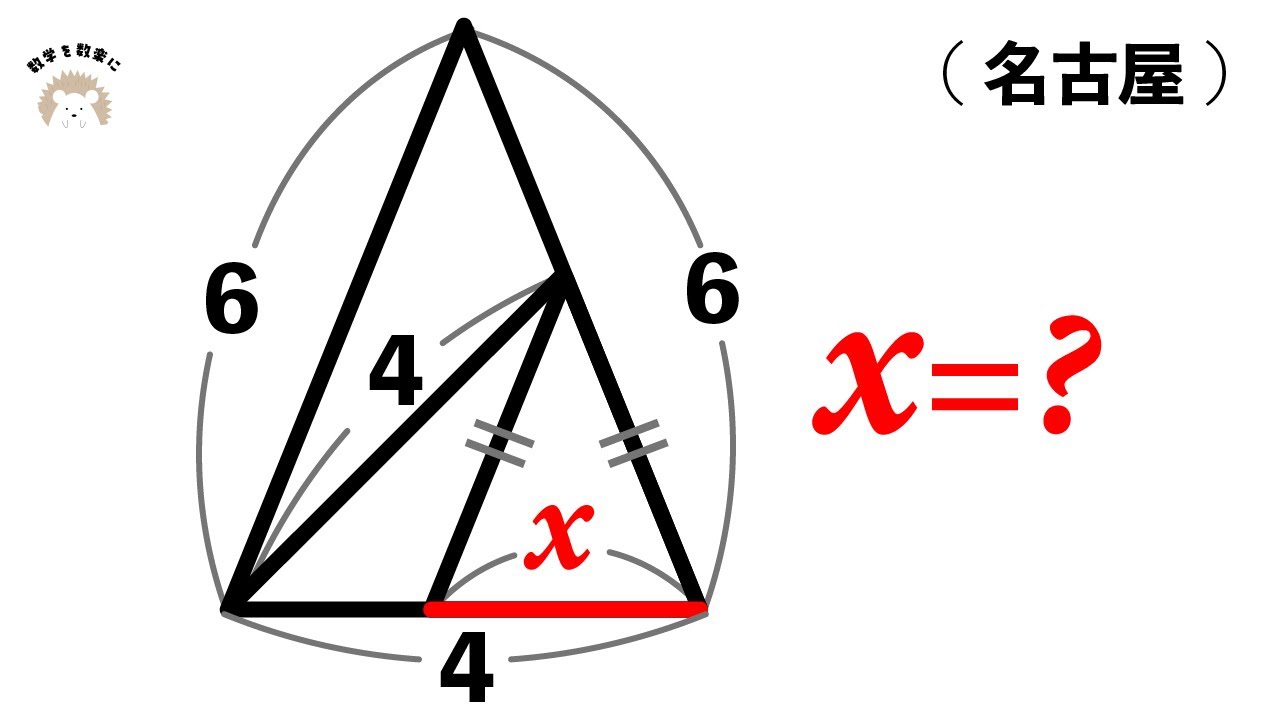
問題文全文(内容文):
高校受験対策・死守45
①$-5+2$を計算しなさい。
②$(x+2)^2$を展開しなさい。
③$y$は$x$に反比例し、比例定数は 3である。
$x$と$y$の関係を式に表しなさい。
④正五角形の内角の和は何度か、求めなさい。
⑤二次方程式 $2x^2-x=0$を解きなさい。
⑥となる自然数$a$をすべて求めなさい。
⑦直線$6x-y=1$0と$x$軸との交点をPとする。
直線$ax-2y=15$が点Pを通るとき、$a$の値を求めなさい。
⑧500円、100円、50円、10円の硬質が1枚ずつある。
この4枚の硬貨を同時に投げるとき、表が出た硬貨の合計金額が、600円以上になる確率を求めなさい。
ただしすべての硬貨の表と裏の出かたは同様に確からしいものとする。
⑨右の図は円錐の展開図です。
この展開図を組み立てたとき、側面となるおうぎ形は半径が16cm、中心角が135°である。
底面となる円の半径を求めなさい。
⑩右の表は、生徒100人の通学時間を度数分布表に表したものである。
$a:b=4:3$であるとき、中央値が含まれる階級の相対度数を求めなさい。
高校受験対策・死守45
①$-5+2$を計算しなさい。
②$(x+2)^2$を展開しなさい。
③$y$は$x$に反比例し、比例定数は 3である。
$x$と$y$の関係を式に表しなさい。
④正五角形の内角の和は何度か、求めなさい。
⑤二次方程式 $2x^2-x=0$を解きなさい。
⑥となる自然数$a$をすべて求めなさい。
⑦直線$6x-y=1$0と$x$軸との交点をPとする。
直線$ax-2y=15$が点Pを通るとき、$a$の値を求めなさい。
⑧500円、100円、50円、10円の硬質が1枚ずつある。
この4枚の硬貨を同時に投げるとき、表が出た硬貨の合計金額が、600円以上になる確率を求めなさい。
ただしすべての硬貨の表と裏の出かたは同様に確からしいものとする。
⑨右の図は円錐の展開図です。
この展開図を組み立てたとき、側面となるおうぎ形は半径が16cm、中心角が135°である。
底面となる円の半径を求めなさい。
⑩右の表は、生徒100人の通学時間を度数分布表に表したものである。
$a:b=4:3$であるとき、中央値が含まれる階級の相対度数を求めなさい。
単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守45
①$-5+2$を計算しなさい。
②$(x+2)^2$を展開しなさい。
③$y$は$x$に反比例し、比例定数は 3である。
$x$と$y$の関係を式に表しなさい。
④正五角形の内角の和は何度か、求めなさい。
⑤二次方程式 $2x^2-x=0$を解きなさい。
⑥となる自然数$a$をすべて求めなさい。
⑦直線$6x-y=1$0と$x$軸との交点をPとする。
直線$ax-2y=15$が点Pを通るとき、$a$の値を求めなさい。
⑧500円、100円、50円、10円の硬質が1枚ずつある。
この4枚の硬貨を同時に投げるとき、表が出た硬貨の合計金額が、600円以上になる確率を求めなさい。
ただしすべての硬貨の表と裏の出かたは同様に確からしいものとする。
⑨右の図は円錐の展開図です。
この展開図を組み立てたとき、側面となるおうぎ形は半径が16cm、中心角が135°である。
底面となる円の半径を求めなさい。
⑩右の表は、生徒100人の通学時間を度数分布表に表したものである。
$a:b=4:3$であるとき、中央値が含まれる階級の相対度数を求めなさい。
高校受験対策・死守45
①$-5+2$を計算しなさい。
②$(x+2)^2$を展開しなさい。
③$y$は$x$に反比例し、比例定数は 3である。
$x$と$y$の関係を式に表しなさい。
④正五角形の内角の和は何度か、求めなさい。
⑤二次方程式 $2x^2-x=0$を解きなさい。
⑥となる自然数$a$をすべて求めなさい。
⑦直線$6x-y=1$0と$x$軸との交点をPとする。
直線$ax-2y=15$が点Pを通るとき、$a$の値を求めなさい。
⑧500円、100円、50円、10円の硬質が1枚ずつある。
この4枚の硬貨を同時に投げるとき、表が出た硬貨の合計金額が、600円以上になる確率を求めなさい。
ただしすべての硬貨の表と裏の出かたは同様に確からしいものとする。
⑨右の図は円錐の展開図です。
この展開図を組み立てたとき、側面となるおうぎ形は半径が16cm、中心角が135°である。
底面となる円の半径を求めなさい。
⑩右の表は、生徒100人の通学時間を度数分布表に表したものである。
$a:b=4:3$であるとき、中央値が含まれる階級の相対度数を求めなさい。
投稿日:2019.12.15