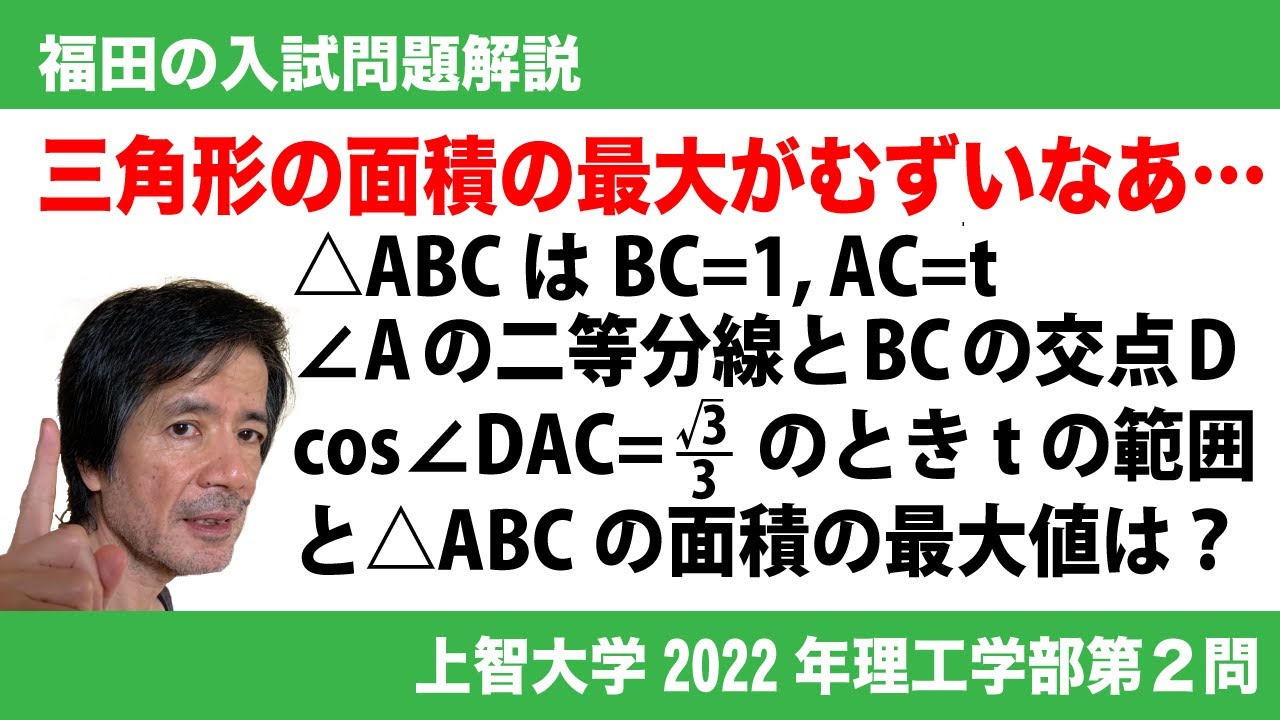
問題文全文(内容文):
$\Large{\boxed{3}}$ $\pi$を円周率とする。$f(x)$=$x^2(x^2-1)$とし、$f(x)$の最小値を$m$とする。
(1)$m$=$\displaystyle\frac{\boxed{\ \ シ\ \ }}{\boxed{\ \ ス\ \ }}$ である。
(2)$y$=$f(x)$で表される曲線を$y$軸の周りに1回転させてできる曲面でできた器に、$y$軸方向から静かに水を注ぐ。
(i)水面が$y$=$a$(ただし$m$≦$a$≦0)になったときの水面の面積は$\boxed{\ \ セ\ \ }$である。
(ii)水面が$y$=0になったときの水の体積は$\displaystyle\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}\pi$ である。
(iii)上方から注ぐ水が単位時間あたり一定量であるとする。水面が$y$=0に達するまでは、水面の面積は、水を注ぎ始めてからの時間の$\displaystyle\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$ 乗に比例して大きくなる。
(iv)水面が$y$=2になったときの水面の面積は$\boxed{\ \ テ\ \ }\pi$であり、水の体積は$\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}\pi$ である。
$\Large{\boxed{3}}$ $\pi$を円周率とする。$f(x)$=$x^2(x^2-1)$とし、$f(x)$の最小値を$m$とする。
(1)$m$=$\displaystyle\frac{\boxed{\ \ シ\ \ }}{\boxed{\ \ ス\ \ }}$ である。
(2)$y$=$f(x)$で表される曲線を$y$軸の周りに1回転させてできる曲面でできた器に、$y$軸方向から静かに水を注ぐ。
(i)水面が$y$=$a$(ただし$m$≦$a$≦0)になったときの水面の面積は$\boxed{\ \ セ\ \ }$である。
(ii)水面が$y$=0になったときの水の体積は$\displaystyle\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}\pi$ である。
(iii)上方から注ぐ水が単位時間あたり一定量であるとする。水面が$y$=0に達するまでは、水面の面積は、水を注ぎ始めてからの時間の$\displaystyle\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$ 乗に比例して大きくなる。
(iv)水面が$y$=2になったときの水面の面積は$\boxed{\ \ テ\ \ }\pi$であり、水の体積は$\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}\pi$ である。
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ $\pi$を円周率とする。$f(x)$=$x^2(x^2-1)$とし、$f(x)$の最小値を$m$とする。
(1)$m$=$\displaystyle\frac{\boxed{\ \ シ\ \ }}{\boxed{\ \ ス\ \ }}$ である。
(2)$y$=$f(x)$で表される曲線を$y$軸の周りに1回転させてできる曲面でできた器に、$y$軸方向から静かに水を注ぐ。
(i)水面が$y$=$a$(ただし$m$≦$a$≦0)になったときの水面の面積は$\boxed{\ \ セ\ \ }$である。
(ii)水面が$y$=0になったときの水の体積は$\displaystyle\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}\pi$ である。
(iii)上方から注ぐ水が単位時間あたり一定量であるとする。水面が$y$=0に達するまでは、水面の面積は、水を注ぎ始めてからの時間の$\displaystyle\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$ 乗に比例して大きくなる。
(iv)水面が$y$=2になったときの水面の面積は$\boxed{\ \ テ\ \ }\pi$であり、水の体積は$\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}\pi$ である。
$\Large{\boxed{3}}$ $\pi$を円周率とする。$f(x)$=$x^2(x^2-1)$とし、$f(x)$の最小値を$m$とする。
(1)$m$=$\displaystyle\frac{\boxed{\ \ シ\ \ }}{\boxed{\ \ ス\ \ }}$ である。
(2)$y$=$f(x)$で表される曲線を$y$軸の周りに1回転させてできる曲面でできた器に、$y$軸方向から静かに水を注ぐ。
(i)水面が$y$=$a$(ただし$m$≦$a$≦0)になったときの水面の面積は$\boxed{\ \ セ\ \ }$である。
(ii)水面が$y$=0になったときの水の体積は$\displaystyle\frac{\boxed{\ \ ソ\ \ }}{\boxed{\ \ タ\ \ }}\pi$ である。
(iii)上方から注ぐ水が単位時間あたり一定量であるとする。水面が$y$=0に達するまでは、水面の面積は、水を注ぎ始めてからの時間の$\displaystyle\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}$ 乗に比例して大きくなる。
(iv)水面が$y$=2になったときの水面の面積は$\boxed{\ \ テ\ \ }\pi$であり、水の体積は$\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}\pi$ である。
投稿日:2023.09.17