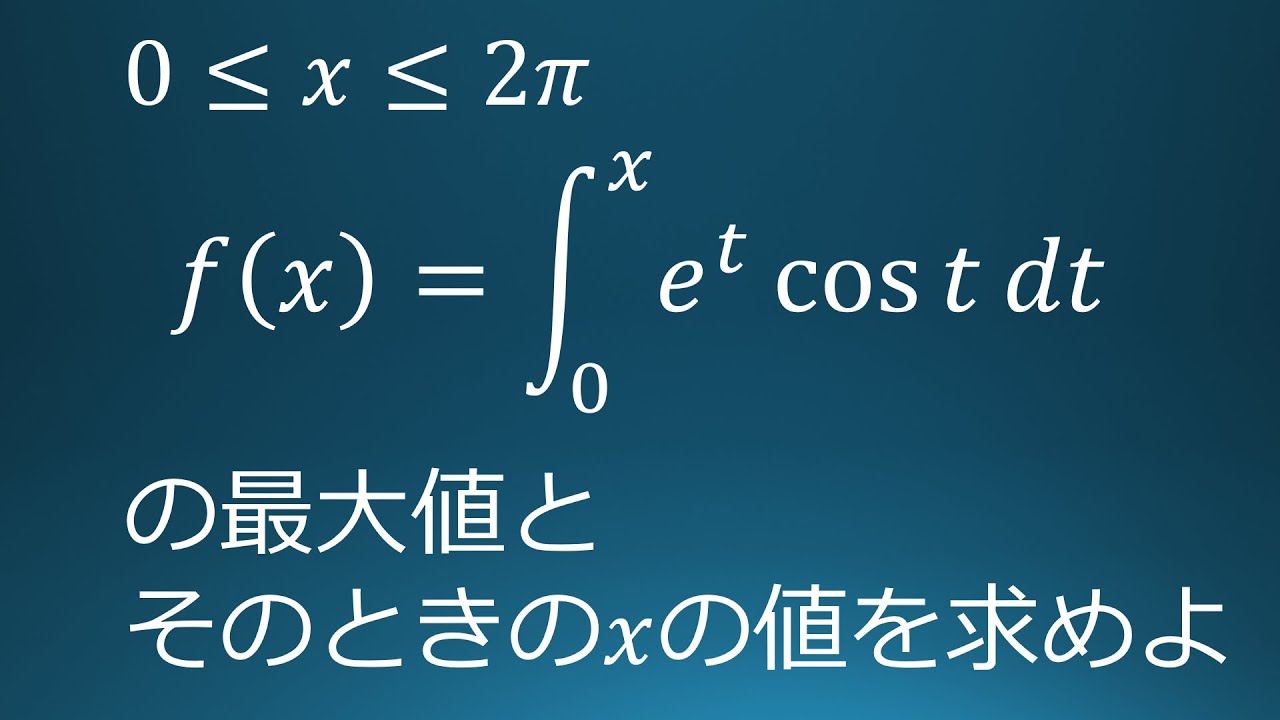篠原京大塾：２０２１年（文系数学）過去問解説【篠原好】

問題文全文(内容文)：
２０２１年（文系数学）過去問解説

単元： #大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)

指導講師：篠原好【京大模試全国一位の勉強法】

問題文全文(内容文)：
２０２１年（文系数学）過去問解説

投稿日：2022.02.01

＜関連動画＞

大学入試問題#775「ほぼ、詰んでる」　横浜国立大学(1998) #定積分

単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#横浜国立大学#数学(高校生)#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：
$\displaystyle \int_{0}^{2\pi} x^2|\sin\ x|\ dx$

出典：1998年横浜国立大学　入試問題

この動画を見る　

群馬大・津田塾大　数列の和・積分　高校数学 Mathematics Japanese university entrance exam

単元： #数Ⅱ#大学入試過去問(数学)#微分法と積分法#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#数学(高校生)#群馬大学#数B#津田塾大学

指導講師：鈴木貫太郎

問題文全文(内容文)：
群馬大学過去問題
$a_k= \frac{(3k+1)(3k+2)}{3k(k+1)}$ (k自然数)
$\displaystyle\sum_{k=1}^n a_k$をnの式で

津田塾大学過去問題
$C:y=x^2-x-4|x-1|$と直線lは2点で接する。
Cとlで囲まれた面積

この動画を見る　

大学入試問題#192　東京大学(昭和9年)　不定積分　3手1組の好手順

単元： #大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ

指導講師：ますただ

問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{1}{x\sqrt{ 1+x^6 }}\ dx$を計算せよ。

出典：昭和9年東京大学　入試問題

この動画を見る　

絶対に取りたい整数問題！分からない時はとにかく実験あるのみ【早稲田大学】【数学入試問題】

単元： #数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)

指導講師：数学・算数の楽しさを思い出した / Ken

問題文全文(内容文)：
$n^2+1,2n^2+3,6n^2+5$がすべて素数となる自然数$n$は$n=1,2$のみであることを示せ。

早稲田大過去問

この動画を見る　

大学入試問題#740「解き方色々」　東京医科大学(2024) 定積分

単元： #大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科大学

指導講師：ますただ

問題文全文(内容文)：
$\displaystyle \int_{-2}^{1} (x+2)(x-1)^7 dx$

出典：2024年東京医科大学　入試問題

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> 篠原京大塾：２０２１年（文系数学）過去問解説【篠原好】

＜関連動画＞

大学入試問題#775「ほぼ、詰んでる」 横浜国立大学(1998) #定積分

群馬大・津田塾大 数列の和・積分 高校数学 Mathematics Japanese university entrance exam

大学入試問題#192 東京大学(昭和9年) 不定積分 3手1組の好手順

絶対に取りたい整数問題！分からない時はとにかく実験あるのみ【早稲田大学】【数学 入試問題】

大学入試問題#740「解き方色々」 東京医科大学(2024) 定積分