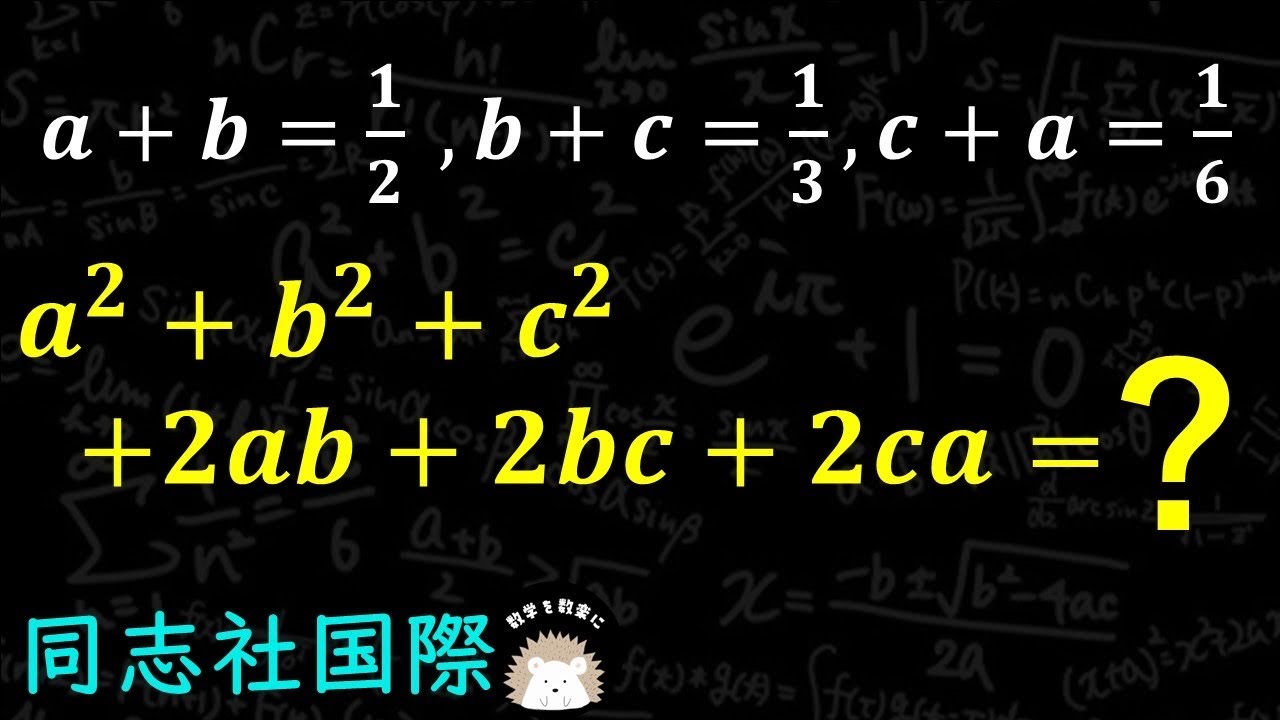連立２元４次方程式

問題文全文(内容文)：
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x+y=1 \\
x^4+y^4=881
\end{array}
\right.
\end{eqnarray}$
これを解け.

単元： #数Ⅰ#数と式#式の計算（整式・展開・因数分解）#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x+y=1 \\
x^4+y^4=881
\end{array}
\right.
\end{eqnarray}$
これを解け.

投稿日：2022.10.17

単元： #数Ⅰ#図形と計量#三角比への応用（正弦・余弦・面積）#数学(高校生)

指導講師：理数個別チャンネル

問題文全文(内容文)：
次の各場合について，$△ABC$ の残りの辺の長さと角の大きさを求めよ。
(1) $b=3，c=\sqrt3，B=60°$
(2) $b=2\sqrt3，c=2，C=30°$

この動画を見る　

単元： #数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)

指導講師：とある男が授業をしてみた

問題文全文(内容文)：
①$x^2-2x-3=0$
②$x^2+7x=0$
③$5x^2-3=0$
④$4x^2+7x-2=0$
⑤$3x^2+10x+3=0$
⑥$4x^2+8x-21=0$

この動画を見る　

単元： #数Ⅰ#図形と計量#三角比（三角比・拡張・相互関係・単位円）#数学(高校生)

教材： #高校リード問題集#高校リード問題集数Ⅰ#中高教材

指導講師：理数個別チャンネル

問題文全文(内容文)：
$0°≦x≦180°$のとき、関数$y=sin²x+cosx+1$の最大値、最小値を求めよ。

この動画を見る　

単元： #数Ⅰ#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#数学(高校生)

指導講師：鈴木貫太郎

問題文全文(内容文)：
これを解け.
$2^x+2^{\vert x\vert}\geqq 2\sqrt2$

この動画を見る　

単元： #数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
abc=1のとき
$\frac{1}{ab+a+1} +\frac{1}{bc+b+1} + \frac{1}{ca+c+1}$
の値を求めよ

この動画を見る　