方程式立てずに解ける！ 大阪教育大附属天王寺 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(中学生) > 中1数学 > 平面図形 > 方程式立てずに解ける！　大阪教育大附属天王寺

方程式立てずに解ける！　大阪教育大附属天王寺

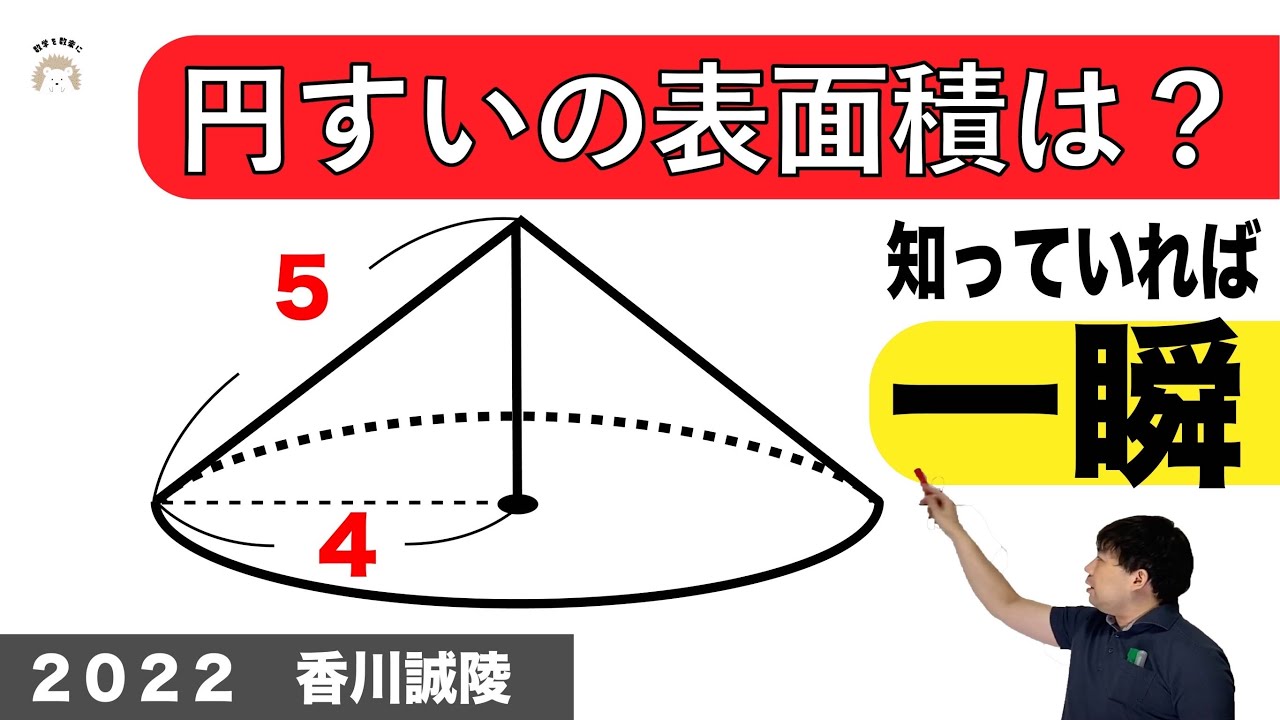
問題文全文(内容文)：
ある正方形の各辺の長さを1cmずつ短くすると面積が半分になった。
もとの正方形の一辺の長さは？

大阪教育大学附属高等学校天王寺校舎
単元： #数学(中学生)#中1数学#文章題#文章題その他#平面図形#高校入試過去問(数学)
指導講師： 数学を数楽に
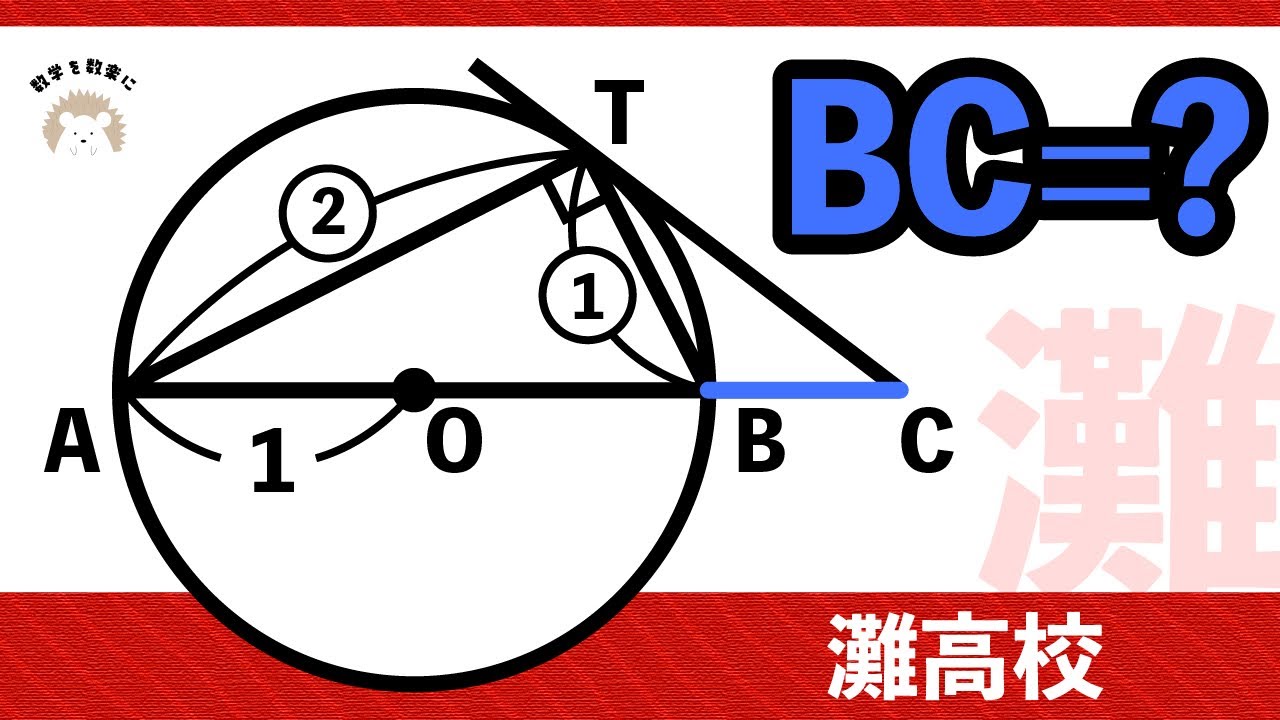
問題文全文(内容文)：
ある正方形の各辺の長さを1cmずつ短くすると面積が半分になった。
もとの正方形の一辺の長さは？

大阪教育大学附属高等学校天王寺校舎
投稿日：2023.04.25

＜関連動画＞

【手早く工夫して…！】空間図形：名古屋女子大学高等学校～全国入試問題解法

アイキャッチ画像
単元： #数学(中学生)#中1数学#空間図形
指導講師： 高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
A:半径4㎝の球、B:Aの二等分、C:Aの四等分の表面積の比を最も簡単な整数の比で表しなさい。
この動画を見る　

【中学数学】99%が間違えた円と接線の問題～2022年埼玉県公立高校入試～【高校受験】

アイキャッチ画像
単元： #数学(中学生)#中1数学#平面図形
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
図のように、点Oを中心とする円周上に２点A,Bをとり、A,Bを通る円Oの接線をそれぞれl,mとします。直線lとmとが点Pで交わる。
直線l,mに接し、円Oに点Qで接する円の中心をRとします。また、点Ｑを通る円Ｏと円Ｒの共通の接線をnとし、lとnとの交点をCとします。
円Ｏの半径が5cm、円Rの半径が3cmであるとき、線分PCの長さを求めよ。

※図は動画内参照
この動画を見る　

立方体に内部にできる三角形の面積

アイキャッチ画像
単元： #数学(中学生)#中1数学#空間図形
指導講師： 数学を数楽に
問題文全文(内容文)：
立体$ABCD-DFGH$は立方体
$\triangle PEF$の面積は何$cm^2$??

出典：東京都立大泉高等学校
この動画を見る　

【中1 数学】中1-54 比例 ・ 反比例の表の特徴

アイキャッチ画像
単元： #数学(中学生)#中1数学#比例・反比例
指導講師： とある男が授業をしてみた
問題文全文(内容文)：
◎yはxに比例する。

①xとyの関係を式に表すと？
②上の表を完成させよう！
③xが2倍、3倍…となるとyはどうなる？

◎yはxに反比例する。

④xとyの関係を式に表すと？
⑤上の表を完成させよう！
⑥xが2倍、3倍…となるとyはどうなる？
②と⑤の表は動画内参照
この動画を見る　

中１数学「正の数・負の数②（反対の性質）」【毎日配信】

アイキャッチ画像
単元： #数学(中学生)#中1数学#正の数・負の数
指導講師： 中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文)：
正の数・負の数②（反対の性質）に関して解説していきます。
この動画を見る　
トップへ戻る