メネラウスの定理が間違ってる？との指摘について - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(高校生) > 数A > 図形の性質 > 内心・外心・重心とチェバ・メネラウス > メネラウスの定理が間違ってる？との指摘について

メネラウスの定理が間違ってる？との指摘について

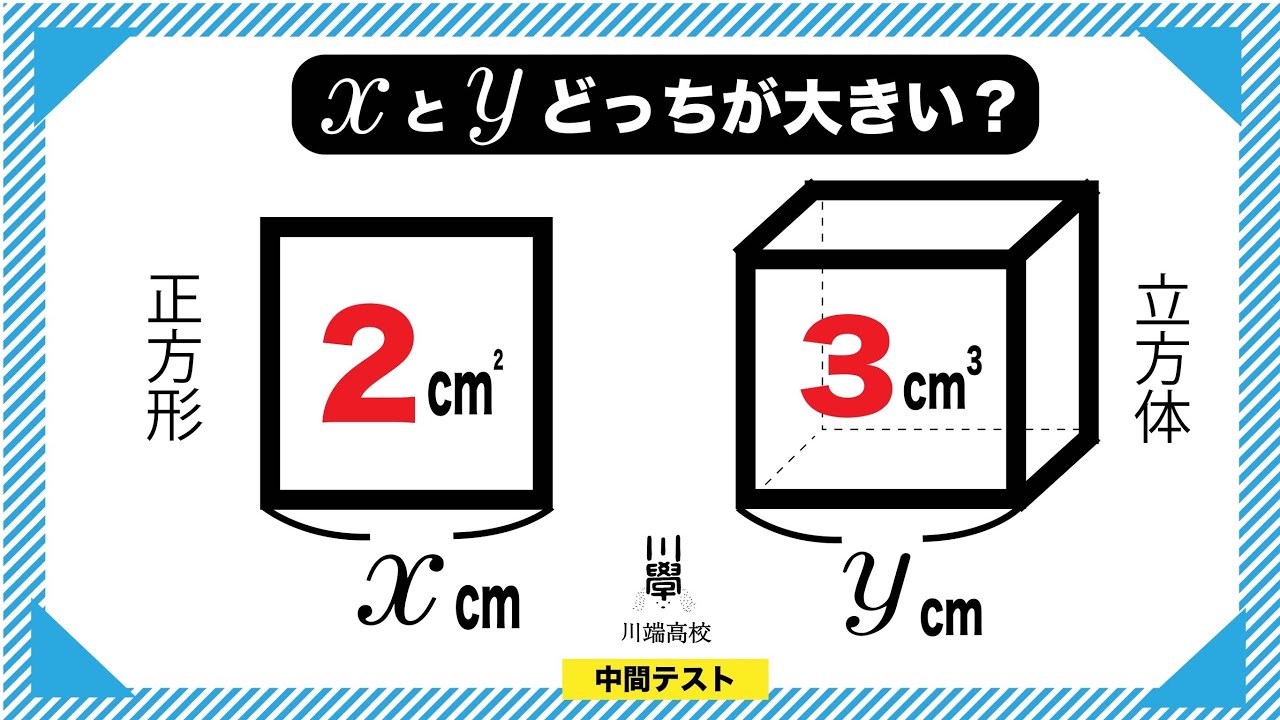
問題文全文(内容文)：
あきとんとんの本「見るだけで理解が加速する　数学公式図鑑」についての問い合わせの回答です。他にも疑問に思ってそうだったので動画にしました.
単元： #数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師： 【楽しい授業動画】あきとんとん
問題文全文(内容文)：
あきとんとんの本「見るだけで理解が加速する　数学公式図鑑」についての問い合わせの回答です。他にも疑問に思ってそうだったので動画にしました.
投稿日：2023.09.17

＜関連動画＞

大学入試問題#90　京都大学(2001)　整数問題

アイキャッチ画像
単元： #数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師： ますただ
問題文全文(内容文)：
$x,y,z$：正の整数
$x^2+2y^2+2z^2-2xy-2xz+2yz-5=0$をみたす組（$x,y,z$）をすべて求めよ。

出典：2001年京都大学　入試問題
この動画を見る　

17兵庫県教員採用試験（数学：1-1 場合の下図）

アイキャッチ画像
単元： #数A#場合の数と確率#場合の数#その他#数学(高校生)#教員採用試験
指導講師： ますただ
問題文全文(内容文)：
1⃣-(1)
3つの頂点で△を作る。
(1)△は全部で何個
(2)3つの辺が全て異なる△の個数
＊図は動画内参照
この動画を見る　

福田のおもしろ数学444〜難しい対数方程式の解

アイキャッチ画像
単元： #数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師： 福田次郎
問題文全文(内容文)：

$\sqrt x=\log_2 x$

を満たす実数$x$をすべて求めてください。
　　　　
この動画を見る　

福田のおもしろ数学305〜四角形に内接する円の半径

アイキャッチ画像
単元： #数Ⅰ#数A#図形の性質#図形と計量#三角比への応用（正弦・余弦・面積）#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師： 福田次郎
問題文全文(内容文)：
図は動画参照
$AP=19,BP=26,CQ=37,DQ=23$
内接円の半径は？
この動画を見る　

横浜市立（医）ド・モアブルと７倍角

アイキャッチ画像
単元： #数A#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師： 鈴木貫太郎
問題文全文(内容文)：
(1)ド・モアブルの定理を用いて$\sin7\theta$を$\sin\theta,\cos\theta$およびその累乗を用いて表せ.
(2)$7x^3-35x^2+21x-1=0$を解け.
(3)$\dfrac{1}{\tan^2\dfrac{\pi}{7}}+\dfrac{1}{\tan^2\dfrac{2\pi}{7}}+\dfrac{1}{\tan^2\dfrac{3\pi}{7}}$の値を求めよ.

2016横浜市立(医)
この動画を見る　
PAGE TOP