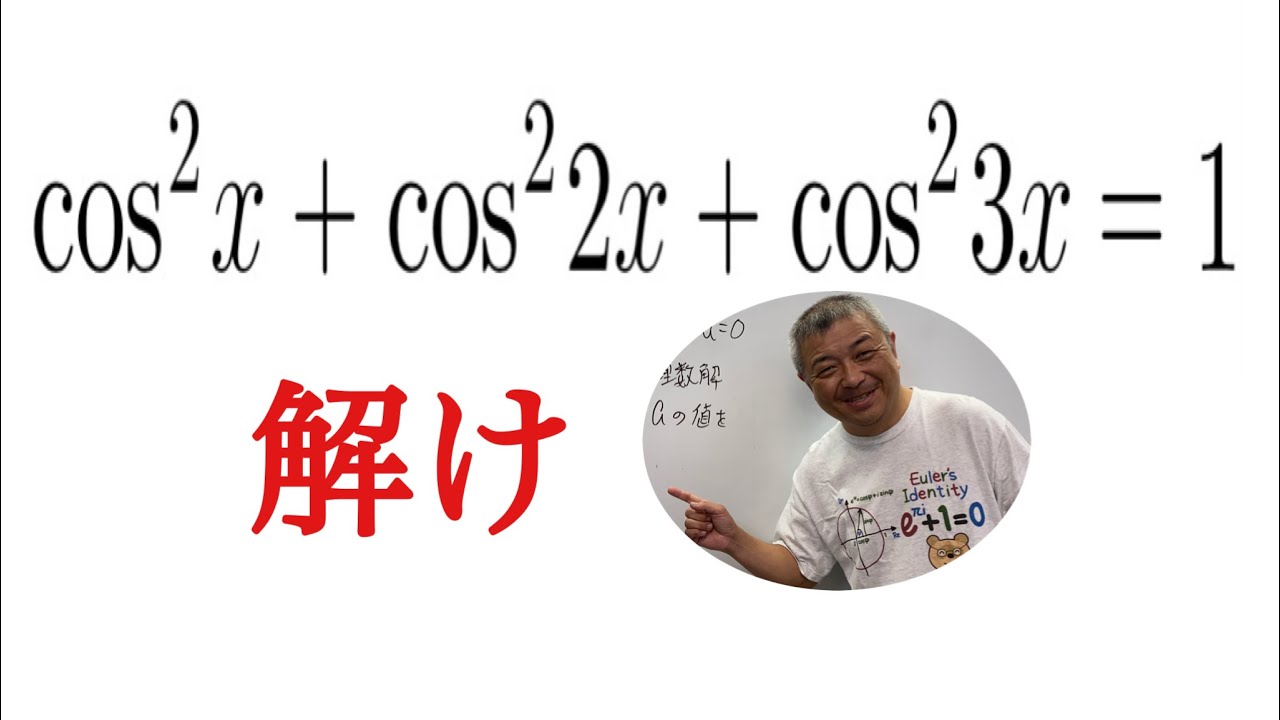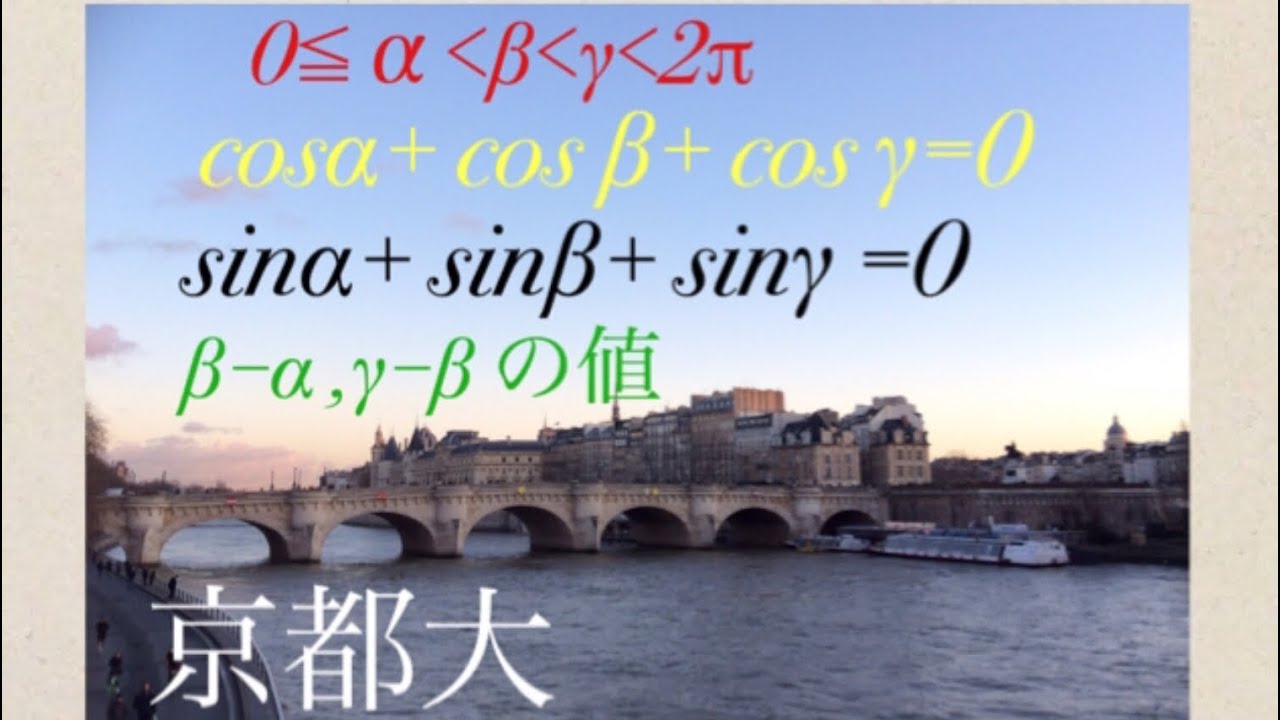加法定理の証明をベクトルで

問題文全文(内容文)：
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
cosα・cosβ+sinα・sinβ =

単元： #数Ⅱ#三角関数#加法定理とその応用#数学(高校生)

指導講師：数学を数楽に

問題文全文(内容文)：
cos(α+β)=cosαcosβ-sinαsinβ
cos(α-β)=cosαcosβ+sinαsinβ
cosα・cosβ+sinα・sinβ =

投稿日：2021.05.23

単元： #数Ⅱ#三角関数#加法定理とその応用#数学(高校生)

指導講師：とある男が授業をしてみた

問題文全文(内容文)：
◎$0 \leqq x \lt 2π$のとき、次の不等式を解こう。

①$\sin x-\sqrt{ 3 } \cos x \gt -1 $

②$\sqrt{ 3 } \sin x - \cos x \leqq \sqrt{ 2 }$

この動画を見る　

単元： #数Ⅱ#三角関数#加法定理とその応用#数学(高校生)

指導講師：福田次郎

問題文全文(内容文)：
$-\dfrac{5}{12}\pi \leqq x \leqq -\dfrac{\pi}{3}$のとき
$y=\tan(x+\dfrac23\pi)-\tan(x+\dfrac\pi6)+\cos(x+\dfrac\pi6)$
の最大値を求めて下さい。

この動画を見る　

単元： #大学入試過去問(数学)#三角関数#加法定理とその応用#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数Ⅲ

指導講師：福田次郎

問題文全文(内容文)：
(3)$0\leqq x\leqq \pi$のとき、次の不等式を解け。
$\sin^2x-\cos^2x+sinx \gt 0$

2022中央大学経済学部過去問

この動画を見る　

単元： #数Ⅱ#三角関数#加法定理とその応用#数学(高校生)

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
加法定理の説明動画です

この動画を見る　

単元： #数Ⅱ#三角関数#加法定理とその応用#数学(高校生)

指導講師：理数個別チャンネル

問題文全文(内容文)：
方程式$\sin(\theta+40°)＝\sin\theta$(ただし$0°\leqq\theta\leqq90°$)をみたす$\theta$を求めよ。

この動画を見る　