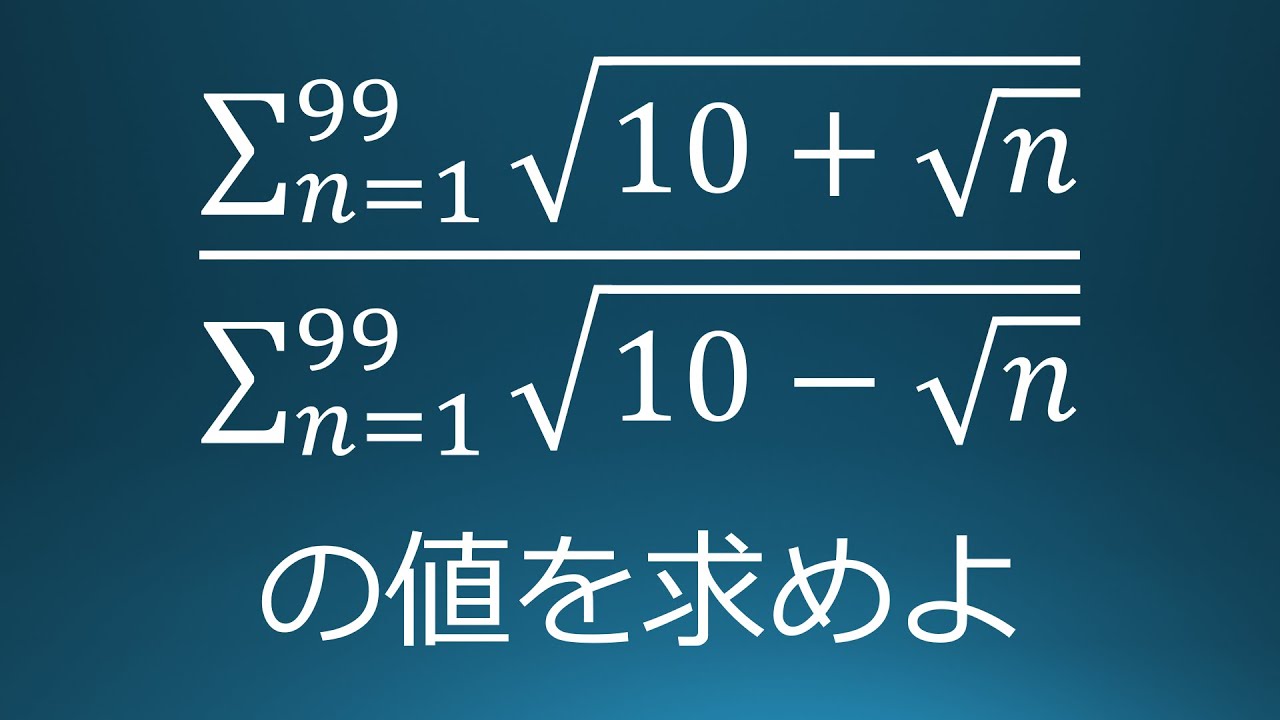問題文全文(内容文):
$a,b,c$は自然数であり,$P$は素数である.
$a+b=b(a-c)$,$c+1=P^2$なら$a+b$か$ab$は平方数であることを示せ.
$a,b,c$は自然数であり,$P$は素数である.
$a+b=b(a-c)$,$c+1=P^2$なら$a+b$か$ab$は平方数であることを示せ.
単元:
#数学検定・数学甲子園・数学オリンピック等#数学オリンピック
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c$は自然数であり,$P$は素数である.
$a+b=b(a-c)$,$c+1=P^2$なら$a+b$か$ab$は平方数であることを示せ.
$a,b,c$は自然数であり,$P$は素数である.
$a+b=b(a-c)$,$c+1=P^2$なら$a+b$か$ab$は平方数であることを示せ.
投稿日:2021.01.20