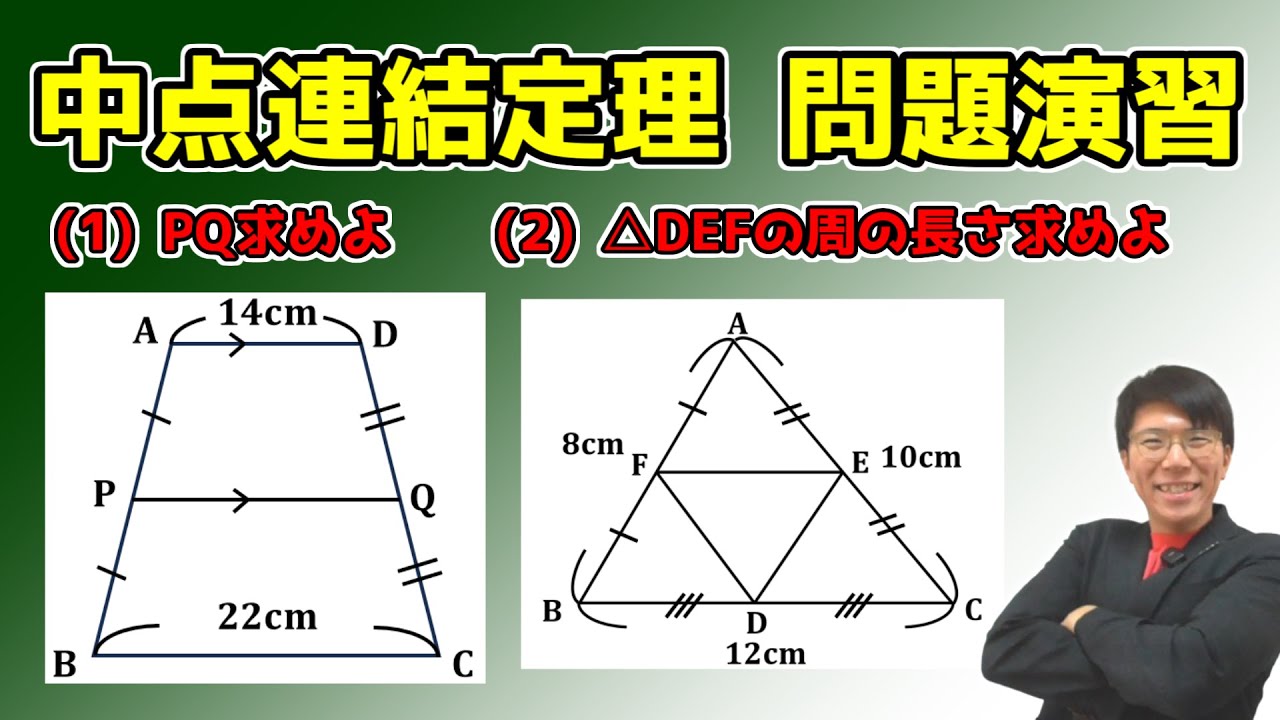
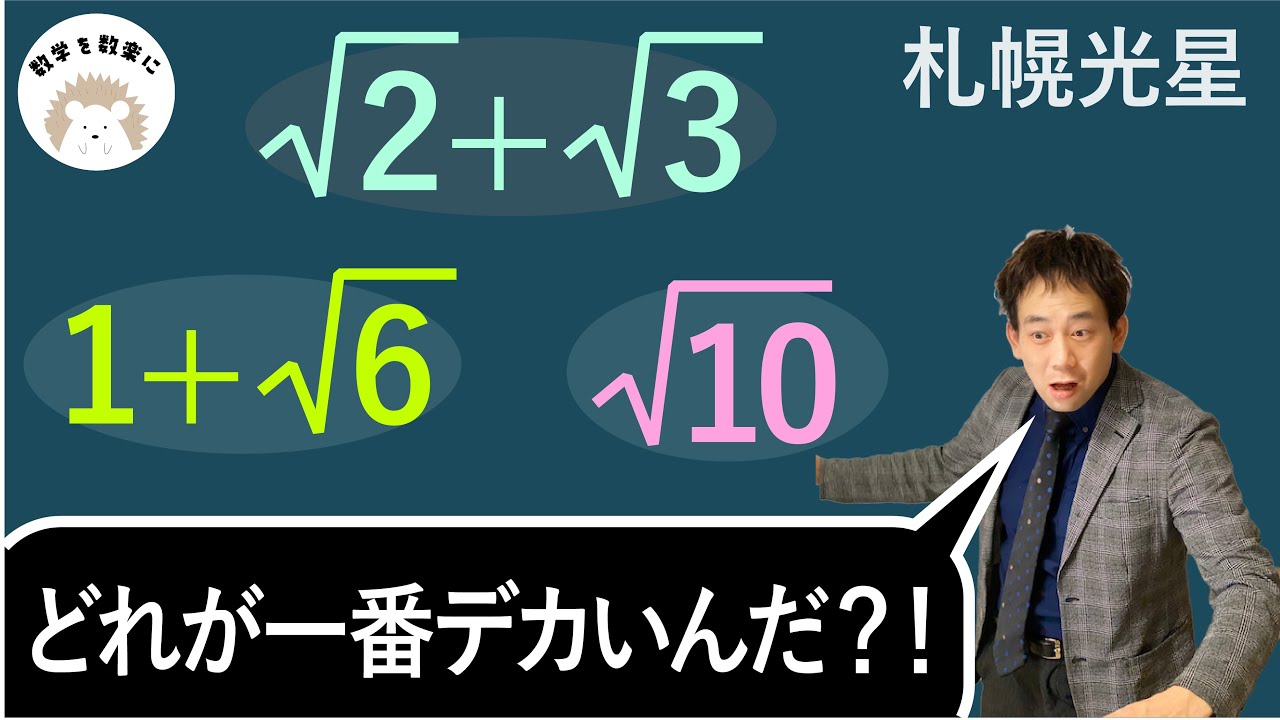問題文全文(内容文):
右の図のように、関数$y = x ^ 2$のグラフ上に2点$A、B$がある。
四角形$AOCB$は長方形であり、点$A$の$x$座標は$-\dfrac{1}{2}$である。
2点$A、C$から$x$軸に垂線$AP、CQ$をそれぞれひくとき、次の問いに答えなさい。
①$△APO$の面積を求めなさい。
②$△APO∞△OQC$である。
このことを用いて、直線$OC$の傾きを求めなさい。
③直線$AB$上に点$M$があり、関数$y = x ^ 2$のグラフ上に点$N(t、t^2)$がある。
点$M$と点$N$の$x$座標が等しいとき、点$M$の座標を$t$を用いて表しなさい。
④点$B$の座標を求めなさい。
⑤$△OQC$の面積を求めなさい。
図は動画内参照
右の図のように、関数$y = x ^ 2$のグラフ上に2点$A、B$がある。
四角形$AOCB$は長方形であり、点$A$の$x$座標は$-\dfrac{1}{2}$である。
2点$A、C$から$x$軸に垂線$AP、CQ$をそれぞれひくとき、次の問いに答えなさい。
①$△APO$の面積を求めなさい。
②$△APO∞△OQC$である。
このことを用いて、直線$OC$の傾きを求めなさい。
③直線$AB$上に点$M$があり、関数$y = x ^ 2$のグラフ上に点$N(t、t^2)$がある。
点$M$と点$N$の$x$座標が等しいとき、点$M$の座標を$t$を用いて表しなさい。
④点$B$の座標を求めなさい。
⑤$△OQC$の面積を求めなさい。
図は動画内参照
単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図のように、関数$y = x ^ 2$のグラフ上に2点$A、B$がある。
四角形$AOCB$は長方形であり、点$A$の$x$座標は$-\dfrac{1}{2}$である。
2点$A、C$から$x$軸に垂線$AP、CQ$をそれぞれひくとき、次の問いに答えなさい。
①$△APO$の面積を求めなさい。
②$△APO∞△OQC$である。
このことを用いて、直線$OC$の傾きを求めなさい。
③直線$AB$上に点$M$があり、関数$y = x ^ 2$のグラフ上に点$N(t、t^2)$がある。
点$M$と点$N$の$x$座標が等しいとき、点$M$の座標を$t$を用いて表しなさい。
④点$B$の座標を求めなさい。
⑤$△OQC$の面積を求めなさい。
図は動画内参照
右の図のように、関数$y = x ^ 2$のグラフ上に2点$A、B$がある。
四角形$AOCB$は長方形であり、点$A$の$x$座標は$-\dfrac{1}{2}$である。
2点$A、C$から$x$軸に垂線$AP、CQ$をそれぞれひくとき、次の問いに答えなさい。
①$△APO$の面積を求めなさい。
②$△APO∞△OQC$である。
このことを用いて、直線$OC$の傾きを求めなさい。
③直線$AB$上に点$M$があり、関数$y = x ^ 2$のグラフ上に点$N(t、t^2)$がある。
点$M$と点$N$の$x$座標が等しいとき、点$M$の座標を$t$を用いて表しなさい。
④点$B$の座標を求めなさい。
⑤$△OQC$の面積を求めなさい。
図は動画内参照
投稿日:2018.01.12