問題文全文(内容文):
${\large第5問}$
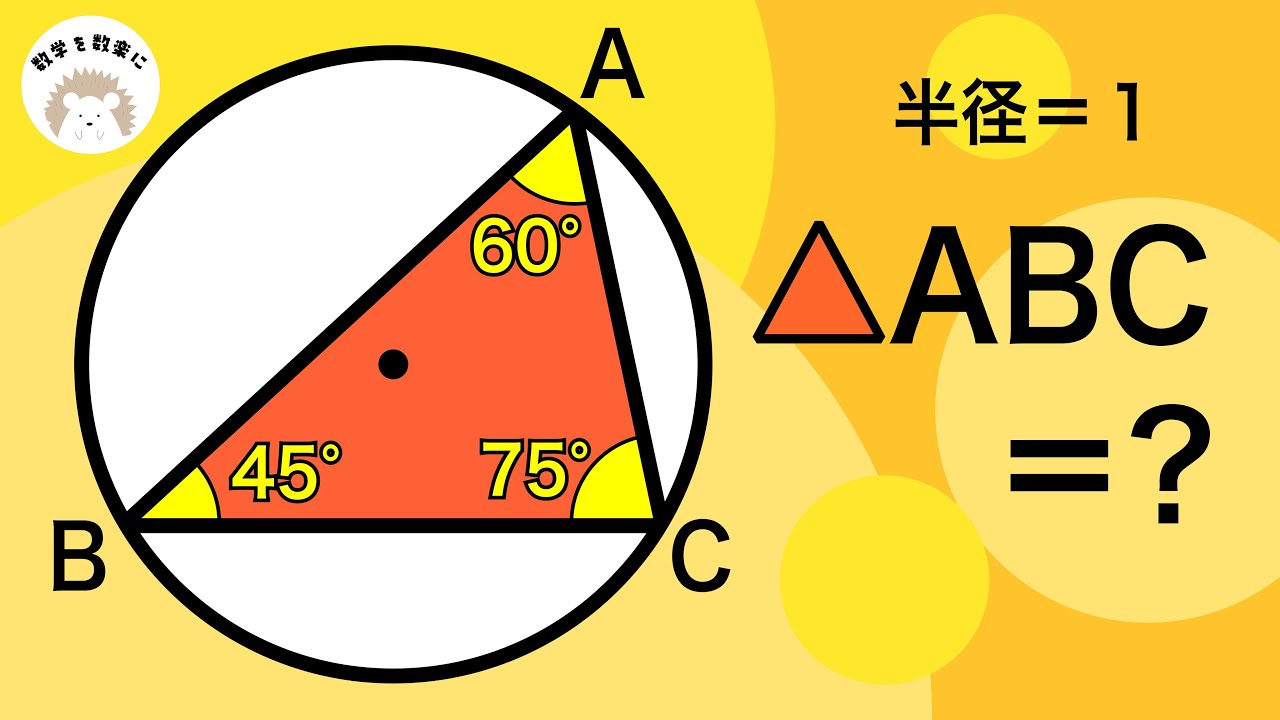
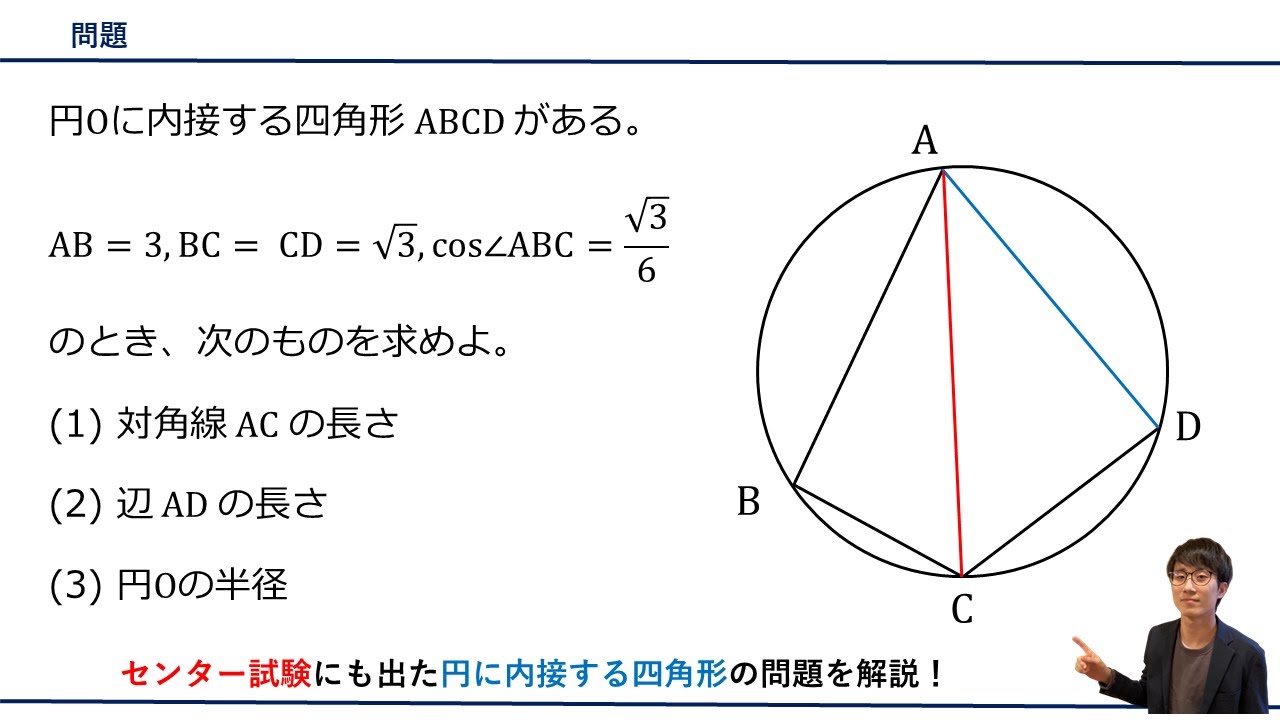
$\triangle ABC$において、辺$BC$を$7:1$に内分する点を$D$とし、辺$AC$を$7:1$に
内分する点を$E$とする。線分$AD$と線分$BE$の交点を$F$とし、直線$CF$
と辺$AB$の交点を$G$とすると
$\displaystyle \frac{GB}{AG}=\boxed{\ \ ア\ \ }, \displaystyle \frac{FD}{AF}=\displaystyle \frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }},$$ \displaystyle \frac{FC}{GF}=\displaystyle \frac{\boxed{\ \ エ\ \ }}{\boxed{\ \ オ\ \ }}$
である。したがって
$\displaystyle \frac{\triangle CDGの面積}{\triangle BFGの面積}=\displaystyle \frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キク\ \ }}\displaystyle$
となる。
4点$B,D,F,G$が同一円周上にあり、かつ$FD=1$のとき
$AB=\boxed{\ \ ケコ\ \ }$
である。さらに、$AE=3\sqrt7$とするとき、$AE・AC=\boxed{\ \ サシ\ \ }$であり
$\angle AEG=\boxed{\ \ ス\ \ }$
である。$\boxed{\ \ ス\ \ }$に当てはまるものを、次の⓪~③のうちから一つ選べ。
⓪$\angle BGE$
①$\angle ADB$
②$\angle ABC$
③$\angle BAD$
2020センター試験過去問
${\large第5問}$
$\triangle ABC$において、辺$BC$を$7:1$に内分する点を$D$とし、辺$AC$を$7:1$に
内分する点を$E$とする。線分$AD$と線分$BE$の交点を$F$とし、直線$CF$
と辺$AB$の交点を$G$とすると
$\displaystyle \frac{GB}{AG}=\boxed{\ \ ア\ \ }, \displaystyle \frac{FD}{AF}=\displaystyle \frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }},$$ \displaystyle \frac{FC}{GF}=\displaystyle \frac{\boxed{\ \ エ\ \ }}{\boxed{\ \ オ\ \ }}$
である。したがって
$\displaystyle \frac{\triangle CDGの面積}{\triangle BFGの面積}=\displaystyle \frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キク\ \ }}\displaystyle$
となる。
4点$B,D,F,G$が同一円周上にあり、かつ$FD=1$のとき
$AB=\boxed{\ \ ケコ\ \ }$
である。さらに、$AE=3\sqrt7$とするとき、$AE・AC=\boxed{\ \ サシ\ \ }$であり
$\angle AEG=\boxed{\ \ ス\ \ }$
である。$\boxed{\ \ ス\ \ }$に当てはまるものを、次の⓪~③のうちから一つ選べ。
⓪$\angle BGE$
①$\angle ADB$
②$\angle ABC$
③$\angle BAD$
2020センター試験過去問
単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#内心・外心・重心とチェバ・メネラウス#方べきの定理と2つの円の関係#センター試験・共通テスト関連#センター試験#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第5問}$
$\triangle ABC$において、辺$BC$を$7:1$に内分する点を$D$とし、辺$AC$を$7:1$に
内分する点を$E$とする。線分$AD$と線分$BE$の交点を$F$とし、直線$CF$
と辺$AB$の交点を$G$とすると
$\displaystyle \frac{GB}{AG}=\boxed{\ \ ア\ \ }, \displaystyle \frac{FD}{AF}=\displaystyle \frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }},$$ \displaystyle \frac{FC}{GF}=\displaystyle \frac{\boxed{\ \ エ\ \ }}{\boxed{\ \ オ\ \ }}$
である。したがって
$\displaystyle \frac{\triangle CDGの面積}{\triangle BFGの面積}=\displaystyle \frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キク\ \ }}\displaystyle$
となる。
4点$B,D,F,G$が同一円周上にあり、かつ$FD=1$のとき
$AB=\boxed{\ \ ケコ\ \ }$
である。さらに、$AE=3\sqrt7$とするとき、$AE・AC=\boxed{\ \ サシ\ \ }$であり
$\angle AEG=\boxed{\ \ ス\ \ }$
である。$\boxed{\ \ ス\ \ }$に当てはまるものを、次の⓪~③のうちから一つ選べ。
⓪$\angle BGE$
①$\angle ADB$
②$\angle ABC$
③$\angle BAD$
2020センター試験過去問
${\large第5問}$
$\triangle ABC$において、辺$BC$を$7:1$に内分する点を$D$とし、辺$AC$を$7:1$に
内分する点を$E$とする。線分$AD$と線分$BE$の交点を$F$とし、直線$CF$
と辺$AB$の交点を$G$とすると
$\displaystyle \frac{GB}{AG}=\boxed{\ \ ア\ \ }, \displaystyle \frac{FD}{AF}=\displaystyle \frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }},$$ \displaystyle \frac{FC}{GF}=\displaystyle \frac{\boxed{\ \ エ\ \ }}{\boxed{\ \ オ\ \ }}$
である。したがって
$\displaystyle \frac{\triangle CDGの面積}{\triangle BFGの面積}=\displaystyle \frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キク\ \ }}\displaystyle$
となる。
4点$B,D,F,G$が同一円周上にあり、かつ$FD=1$のとき
$AB=\boxed{\ \ ケコ\ \ }$
である。さらに、$AE=3\sqrt7$とするとき、$AE・AC=\boxed{\ \ サシ\ \ }$であり
$\angle AEG=\boxed{\ \ ス\ \ }$
である。$\boxed{\ \ ス\ \ }$に当てはまるものを、次の⓪~③のうちから一つ選べ。
⓪$\angle BGE$
①$\angle ADB$
②$\angle ABC$
③$\angle BAD$
2020センター試験過去問
投稿日:2020.01.23