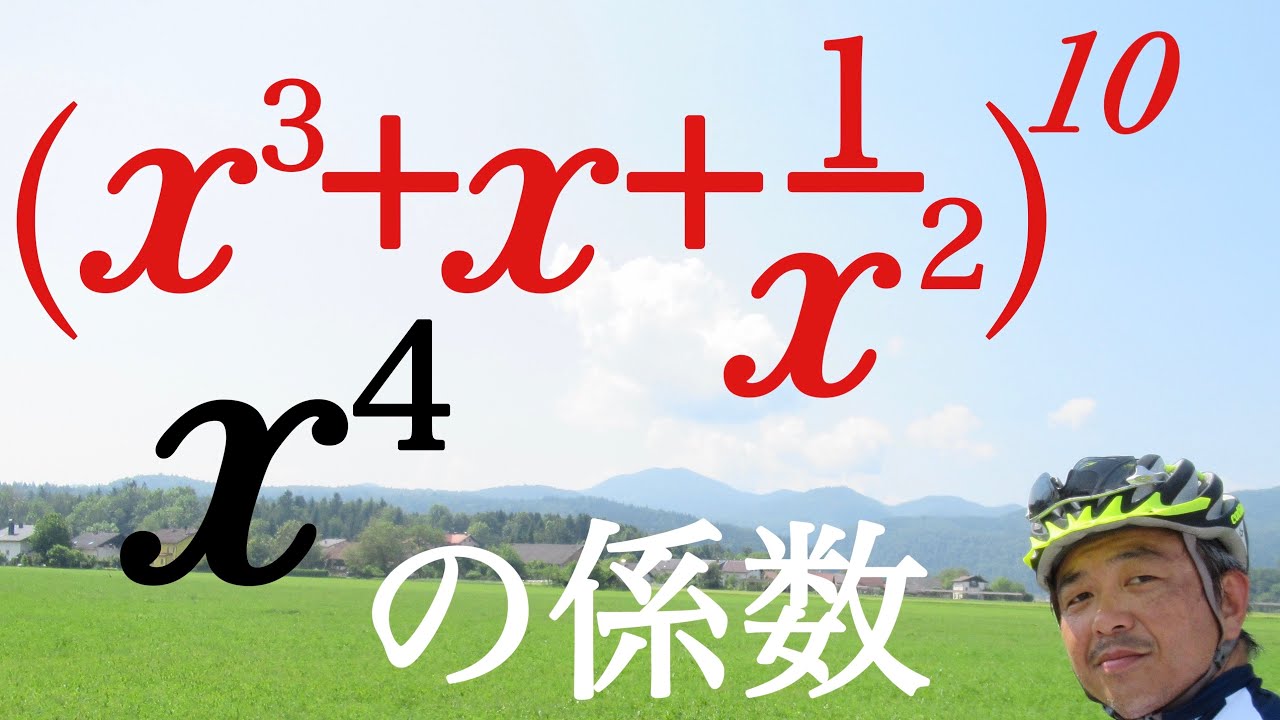問題文全文(内容文):
$ \boxed{1}$
(1)$ -1+4\div \dfrac{2}{3}$
(2)$ 3(2a+5b)-(a+2b)$
(3)$ (x-2)(x+2)+(x-1)(x+4)$
(4)$ x^2+5x+3=0 $
$ \boxed{2}$
(1)点Pの座標は?
(2)y軸上に点Q,Qのy座標をt($ t \gt 4 $)とする.
Qを通り,x軸に平行な直線とb,mの交点をR,Sとする.
①t=6のとき,$ \triangle PRS $は?
②$ \triangle PRS $の面積が$ \triangle ABP $の5倍であるとき,tは?
$ \boxed{3}$
円周上にA,B,C,D,Eがある.
$AC=AE$,$\stackrel{\huge\frown}{BC}$=$\stackrel{\huge\frown}{DE}$であり,交点$ F,G$である.
(1)$ \triangle ABC \equiv \triangle AGE $を証明せよ.
(2)$ AB=4 $cm,$ AE=6$cm,$ DG=3 $cmのとき,
①$ AF=? $
②$ \triangle ABG $と$ \triangle CEF $の面積比を求めよ.
$ \boxed{1}$
(1)$ -1+4\div \dfrac{2}{3}$
(2)$ 3(2a+5b)-(a+2b)$
(3)$ (x-2)(x+2)+(x-1)(x+4)$
(4)$ x^2+5x+3=0 $
$ \boxed{2}$
(1)点Pの座標は?
(2)y軸上に点Q,Qのy座標をt($ t \gt 4 $)とする.
Qを通り,x軸に平行な直線とb,mの交点をR,Sとする.
①t=6のとき,$ \triangle PRS $は?
②$ \triangle PRS $の面積が$ \triangle ABP $の5倍であるとき,tは?
$ \boxed{3}$
円周上にA,B,C,D,Eがある.
$AC=AE$,$\stackrel{\huge\frown}{BC}$=$\stackrel{\huge\frown}{DE}$であり,交点$ F,G$である.
(1)$ \triangle ABC \equiv \triangle AGE $を証明せよ.
(2)$ AB=4 $cm,$ AE=6$cm,$ DG=3 $cmのとき,
①$ AF=? $
②$ \triangle ABG $と$ \triangle CEF $の面積比を求めよ.
単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#1次関数#2次関数#円
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ -1+4\div \dfrac{2}{3}$
(2)$ 3(2a+5b)-(a+2b)$
(3)$ (x-2)(x+2)+(x-1)(x+4)$
(4)$ x^2+5x+3=0 $
$ \boxed{2}$
(1)点Pの座標は?
(2)y軸上に点Q,Qのy座標をt($ t \gt 4 $)とする.
Qを通り,x軸に平行な直線とb,mの交点をR,Sとする.
①t=6のとき,$ \triangle PRS $は?
②$ \triangle PRS $の面積が$ \triangle ABP $の5倍であるとき,tは?
$ \boxed{3}$
円周上にA,B,C,D,Eがある.
$AC=AE$,$\stackrel{\huge\frown}{BC}$=$\stackrel{\huge\frown}{DE}$であり,交点$ F,G$である.
(1)$ \triangle ABC \equiv \triangle AGE $を証明せよ.
(2)$ AB=4 $cm,$ AE=6$cm,$ DG=3 $cmのとき,
①$ AF=? $
②$ \triangle ABG $と$ \triangle CEF $の面積比を求めよ.
$ \boxed{1}$
(1)$ -1+4\div \dfrac{2}{3}$
(2)$ 3(2a+5b)-(a+2b)$
(3)$ (x-2)(x+2)+(x-1)(x+4)$
(4)$ x^2+5x+3=0 $
$ \boxed{2}$
(1)点Pの座標は?
(2)y軸上に点Q,Qのy座標をt($ t \gt 4 $)とする.
Qを通り,x軸に平行な直線とb,mの交点をR,Sとする.
①t=6のとき,$ \triangle PRS $は?
②$ \triangle PRS $の面積が$ \triangle ABP $の5倍であるとき,tは?
$ \boxed{3}$
円周上にA,B,C,D,Eがある.
$AC=AE$,$\stackrel{\huge\frown}{BC}$=$\stackrel{\huge\frown}{DE}$であり,交点$ F,G$である.
(1)$ \triangle ABC \equiv \triangle AGE $を証明せよ.
(2)$ AB=4 $cm,$ AE=6$cm,$ DG=3 $cmのとき,
①$ AF=? $
②$ \triangle ABG $と$ \triangle CEF $の面積比を求めよ.
投稿日:2023.03.02