勘で英検合格する確率は？

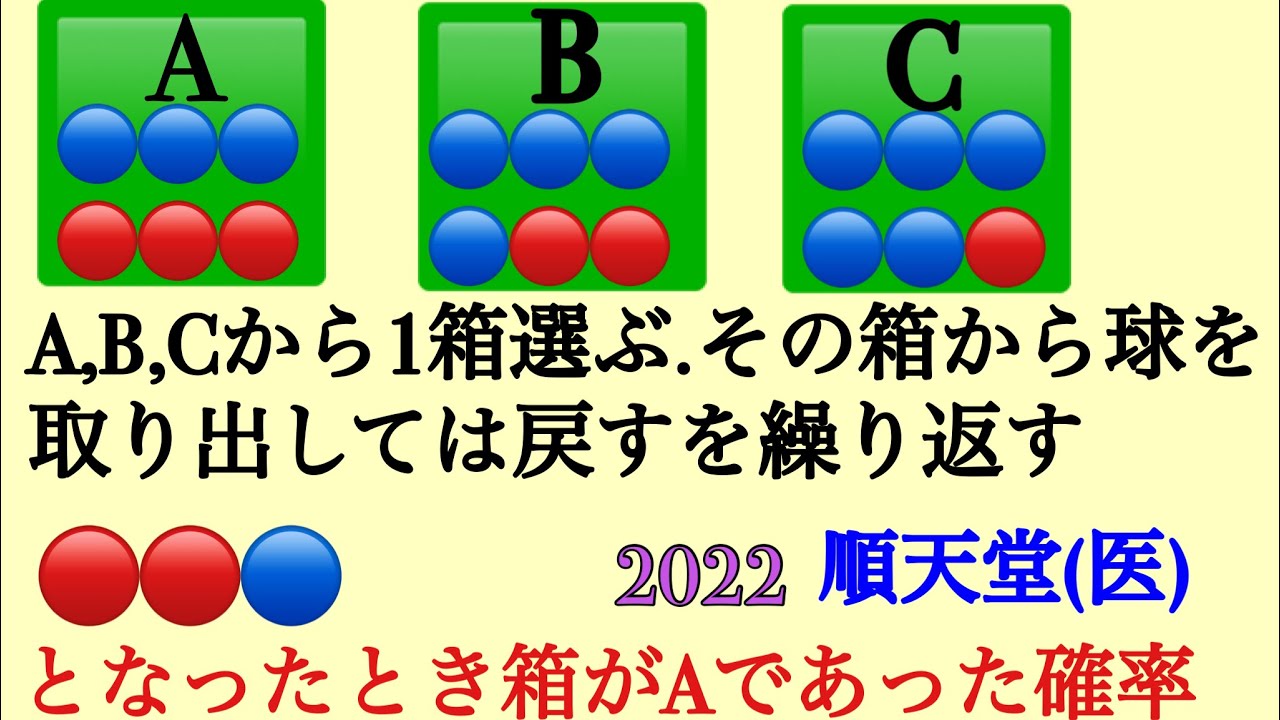
問題文全文(内容文)：
下記質問の解説動画です
全部勘で英検やって合格する確率ってどれくらいですか？

チャプター：

00:00 はじまり

単元： #数A#場合の数と確率#数学(高校生)

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
下記質問の解説動画です
全部勘で英検やって合格する確率ってどれくらいですか？

投稿日：2023.01.22

＜関連動画＞

福田の1.5倍速演習〜合格する重要問題095〜明治大学2020年度理工学部第１問(3)〜円順列と確率

単元： #数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)

指導講師：福田次郎

問題文全文(内容文)：

1

(3)A, B, C, D, Eの5人が、無作為に並び、手をつないでひとつの輪を作るという試行を考える。
(a)この試行を1回行うとき、AがBとCの2人と手をつなぐ確率は

\frac{コ}{サ}

である。
(b)この試行を3回行うとき、Aと3回手をつなぐ人が2人いる確率は

\frac{シ}{ス セ}

である。
(c)この試行を3回行うとき、Aと3回手をつなぐ人が1人だけいる確率は

\frac{ソ}{タ}

である。

2020明治大学理工学部過去問

この動画を見る　

京大の確率の問題！解けますか？【数学入試問題】【京都大学】

単元： #数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)

指導講師：数学・算数の楽しさを思い出した / Ken

問題文全文(内容文)：
さいころを

n

個同時に投げるとき、出た目の数の和が

n + 3

になる確率を求めよ。

京都大過去問

この動画を見る　

福田の数学〜明治大学2021年理工学部第２問〜格子点と確率

単元： #数A#場合の数と確率#確率#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#大学入試解答速報#数学#明治大学#数B

指導講師：福田次郎

問題文全文(内容文)：

2

　nを正の整数とする。座標平面上の点でx座標とy座標がともに整数であるもの
を格子点と呼ぶ。

| x | + | y | = 2 n

を満たす格子点(x,\ y)全体の集合を

D_{2 n}

とする。
(1)

D_{4}

は

あ

個の点からなる。一般に、

D_{2 n}

は

い

個の点からなる。
(2)

D_{2 n}

に属する点

(x, y)

で

| x - 2 n | + | y | = 2 n

を満たすものは全部で

う

個ある。
(3)

D_{2 n}

に属する点

(x, y)

で

| x - n | + | y - n | = 2 n

を満たすものは全部で

え

個ある。
(4)

D_{2 n}

から異なる2点

(x_{1}, y_{1}), (x_{2}, y_{2})

を無作為に選ぶとき、

| x_{1} - x_{2} | + | y_{1} - y_{2} | = 2 n

が成り立つ確率は

お

である。

2021明治大学理工学部過去問

この動画を見る　

【高校数学】　　数Ａ－２５　　確率⑦　・　色玉編 Part.3

単元： #数A#場合の数と確率#確率#数学(高校生)

指導講師：とある男が授業をしてみた

問題文全文(内容文)：
◎Aの袋には赤玉6個と白玉4個、Bの袋には赤玉4個と白玉6個が入っている。
①A,Bの袋からそれぞれ玉を1個とり出すとき、玉の色が異なる確率は？
②A,Bの袋からそれぞれ玉を2個とり出すとき、4個すべて同じ色である確率は？

この動画を見る　

佐藤さんですか？と聞いて当たる確率は？

単元： #数A#場合の数と確率#確率

指導講師：【楽しい授業動画】あきとんとん

問題文全文(内容文)：
下記質問の解説動画です
街中の人に「あなたは佐藤さんですか？」って聞いて的中する確率は？

この動画を見る　

<img src="https://kaiketsu-db.net/wp-content/uploads/2021/11/112-book-morph-outline.gif" alt="" data-eio="l"> 勘で英検合格する確率は？

＜関連動画＞

福田の1.5倍速演習〜合格する重要問題095〜明治大学2020年度理工学部第１問(3)〜円順列と確率

京大の確率の問題！解けますか？【数学 入試問題】【京都大学】

福田の数学〜明治大学2021年理工学部第２問〜格子点と確率

【高校数学】 数Ａ－２５ 確率⑦ ・ 色玉編 Part.3

佐藤さんですか？と聞いて当たる確率は？