 こばちゃん塾
こばちゃん塾
 こばちゃん塾
こばちゃん塾
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【中学受験算数】計算間違いを当てるクイズ!おっちょこちょいを救おう!【毎日1題中学受験算数45】

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
こばちゃん塾
問題文全文(内容文):
2つの数の和を求めるのをまちがえて、差を求めてしまったので、答えは23になりました。これは正しい答えと14ちがいます。
2つの数をそれぞれ求めましょう。
この動画を見る
2つの数の和を求めるのをまちがえて、差を求めてしまったので、答えは23になりました。これは正しい答えと14ちがいます。
2つの数をそれぞれ求めましょう。
【中学受験算数】算数クイズ!2人の年齢を当てろ!分かるかな?【毎日1題中学受験算数44】

単元:
#算数(中学受験)#計算と数の性質#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
こばちゃん塾
問題文全文(内容文):
お父さんとただし君の3年後の年れいの合計は58才、2年前の年れいの差は32歳です。現在のお父さんの年れいを求めましょう。
この動画を見る
お父さんとただし君の3年後の年れいの合計は58才、2年前の年れいの差は32歳です。現在のお父さんの年れいを求めましょう。
【中学受験算数】中学受験初心者が身につけるべき特殊算3選!それぞれ分かりやすく解説します!【毎日1題中学受験算数43(番外編)】

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
こばちゃん塾
問題文全文(内容文):
例 24mの道の片側に6m間隔で木を植える。
1.間隔の数はいくつ?
2.両端に木を植えると、木は何本?
3.両端に電柱を立てると木は何本?
この動画を見る
例 24mの道の片側に6m間隔で木を植える。
1.間隔の数はいくつ?
2.両端に木を植えると、木は何本?
3.両端に電柱を立てると木は何本?
【小4算数】小数の表し方と仕組み!知ってる? 小4算数基礎講座 第14回

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
こばちゃん塾
問題文全文(内容文):
例題
2.35Lになるように下の図に色をぬりましょう
例題
次の数を( )の中の単位で表しましょう
①1kg 782g(kg) ②1403mL(L)
例題
次の数はいくつですか。
①0.01を7こと0.001を4こあわせた数
②0.001を927こ集めた数
③0.001を1324こ集めた数
例題
3.19を10倍、100倍した数をかきましょう。また、10や100でわった数をかきましょう。
この動画を見る
例題
2.35Lになるように下の図に色をぬりましょう
例題
次の数を( )の中の単位で表しましょう
①1kg 782g(kg) ②1403mL(L)
例題
次の数はいくつですか。
①0.01を7こと0.001を4こあわせた数
②0.001を927こ集めた数
③0.001を1324こ集めた数
例題
3.19を10倍、100倍した数をかきましょう。また、10や100でわった数をかきましょう。
【中学受験算数】N進法はこう使え!!不吉な数「4」と「9」を使わない病院での病室番号ってどうなるの?【毎日1題中学受験算数42】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
こばちゃん塾
問題文全文(内容文):
ある病院では、病室番号に「4」と「9」はよくない番号と考え、1号室、2号室、3号室、5号室、6号室、7号室、8号室、10号室、11号室・・・というふうにその2つの番号を使わずに病室番号を割り当てています。
(1)100番目の病室番号はいくつ?
(2)637号室は何番目の病院ですか。
この動画を見る
ある病院では、病室番号に「4」と「9」はよくない番号と考え、1号室、2号室、3号室、5号室、6号室、7号室、8号室、10号室、11号室・・・というふうにその2つの番号を使わずに病室番号を割り当てています。
(1)100番目の病室番号はいくつ?
(2)637号室は何番目の病院ですか。
【連立方程式】列車がトンネルに隠れる問題!苦手な人多し!!【生徒からの質問15】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
指導講師:
こばちゃん塾
問題文全文(内容文):
ある列車が、一定の速さで長さ1200mのトンネルを通る時、列車全体がトンネルに隠れていたのは40秒間であった。また、この列車が同じ速さで長さ256mの駅のホームを通過し始めてから通過し終わるまでに16秒かかった。
この列車の長さと速さをそれぞれ求めましょう。
この動画を見る
ある列車が、一定の速さで長さ1200mのトンネルを通る時、列車全体がトンネルに隠れていたのは40秒間であった。また、この列車が同じ速さで長さ256mの駅のホームを通過し始めてから通過し終わるまでに16秒かかった。
この列車の長さと速さをそれぞれ求めましょう。
【連立方程式】時間の単位変換を使う「速さ」の連立方程式!【生徒からの質問14】

単元:
#算数(中学受験)#速さ#点の移動・時計算
指導講師:
こばちゃん塾
問題文全文(内容文):
A地点からB地点までの道のりは20krである。途中までは車に乗って時速30kmで進み、残りの道のりを時速4kmで歩くと、1時間45分かかった。車で進んだ道のりと、歩いた道のりをそれぞれ求めましょう。
この動画を見る
A地点からB地点までの道のりは20krである。途中までは車に乗って時速30kmで進み、残りの道のりを時速4kmで歩くと、1時間45分かかった。車で進んだ道のりと、歩いた道のりをそれぞれ求めましょう。
【中学受験算数】1分でひらめかないとヤバイ!?超基本の算数クイズ【毎日1題中学受験算数41】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
こばちゃん塾
問題文全文(内容文):
△が3個集まると▢1個に置き換え、▢が3個集まると○1個に置き換え、○が3個集まると☆1個に置き換えます。
(1)△41個をできるだけ少ない記号で表しましょう。
(2)☆☆○▢▢△は、△いくつ分ですか。
この動画を見る
△が3個集まると▢1個に置き換え、▢が3個集まると○1個に置き換え、○が3個集まると☆1個に置き換えます。
(1)△41個をできるだけ少ない記号で表しましょう。
(2)☆☆○▢▢△は、△いくつ分ですか。
【中学受験算数】N進法を使った記号問題!規則を見破れるかな?【毎日1題中学受験算数40】

単元:
#算数(中学受験)#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
こばちゃん塾
問題文全文(内容文):
整数を次のように表すとき、あとの問いに答えましょう。
1 ▢▢▢▢■ 2 ▢▢▢■▢ 3 ▢▢▢■■ 4 ▢▢■▢▢ 5 ▢▢■▢■
(1)■■▢▢■はいくつ?
(2)この方法で表せる最大の数はいくつ?
この動画を見る
整数を次のように表すとき、あとの問いに答えましょう。
1 ▢▢▢▢■ 2 ▢▢▢■▢ 3 ▢▢▢■■ 4 ▢▢■▢▢ 5 ▢▢■▢■
(1)■■▢▢■はいくつ?
(2)この方法で表せる最大の数はいくつ?
【小4算数】ひし形ってどんな形?対角線ってなぁに? 小4算数基礎講座 第13回

単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
こばちゃん塾
問題文全文(内容文):
・下の図形はひし形です。辺ADに平行な辺はどれですか。また、角Aと大きさの等しい角はどれですか。
・下のひし形で、辺AB、辺CD、辺ADの長さは何㎝ですか。また、角A、角Bの大きさは何度ですか。
・下の図のように交わった2本の直線が対角線になる四角形は何という名前の四角形ですか。
・下の文で、正しいものには○を、まちがっているものには✖をつけましょう。
①( )ひし形の2本の対角線は垂直で、それぞれの真ん中で交わる。
②( )長方形も正方形も、対角線が垂直に交わる。
③( )対角線の長さが等しい四角形は、長方形だけです。
④( )平行四辺形では、対角線が交わった点から4つの頂点までの長さがすべて等しい。
*図は動画内参照
この動画を見る
・下の図形はひし形です。辺ADに平行な辺はどれですか。また、角Aと大きさの等しい角はどれですか。
・下のひし形で、辺AB、辺CD、辺ADの長さは何㎝ですか。また、角A、角Bの大きさは何度ですか。
・下の図のように交わった2本の直線が対角線になる四角形は何という名前の四角形ですか。
・下の文で、正しいものには○を、まちがっているものには✖をつけましょう。
①( )ひし形の2本の対角線は垂直で、それぞれの真ん中で交わる。
②( )長方形も正方形も、対角線が垂直に交わる。
③( )対角線の長さが等しい四角形は、長方形だけです。
④( )平行四辺形では、対角線が交わった点から4つの頂点までの長さがすべて等しい。
*図は動画内参照
【中学受験算数】N進法を徹底解説!中学受験でもぜひ覚えておきたいテクニックです!【毎日1題中学受験算数39(番外編)】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
こばちゃん塾
問題文全文(内容文):
例題
・2進法で表された数字は10進法に、10進法で表された数字は2進法に直しましょう。
(1)$15_{(10)}=\underline{ 1111}{}_{(2)} $
(2)$11011_{(2)}=_____{(10)}$
・3進法で表された数字は10進法に、10進法で表された数字は3進法に直しましょう。
(1)$79_{(10)}=_____{(3)} $
(2)$1212_{(3)}=_____{(10)}$
この動画を見る
例題
・2進法で表された数字は10進法に、10進法で表された数字は2進法に直しましょう。
(1)$15_{(10)}=\underline{ 1111}{}_{(2)} $
(2)$11011_{(2)}=_____{(10)}$
・3進法で表された数字は10進法に、10進法で表された数字は3進法に直しましょう。
(1)$79_{(10)}=_____{(3)} $
(2)$1212_{(3)}=_____{(10)}$
生徒からの質問11 列車が鉄橋とトンネルを通る問題!!

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
指導講師:
こばちゃん塾
問題文全文(内容文):
ある列車が、1200mの鉄橋を渡りはじめてから渡り終わるまでに54秒かかった。また、この列車が、850mのトンネルに入りはじめてから完全にでるまでに40秒かかった。
列車の長さを×m,列車の速さを秒速ymとして、列車の長さと速さを求めましょう。
この動画を見る
ある列車が、1200mの鉄橋を渡りはじめてから渡り終わるまでに54秒かかった。また、この列車が、850mのトンネルに入りはじめてから完全にでるまでに40秒かかった。
列車の長さを×m,列車の速さを秒速ymとして、列車の長さと速さを求めましょう。
【中学受験算数】難問!?階段の上り方!フィボナッチ数列って知ってる?【毎日1題中学受験算数38】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
こばちゃん塾
問題文全文(内容文):
10段の階段を1段ずつ、または2段ずつ、また1段と2段を混ぜて上るとき、全部で何通りの上り方がありますか。
この動画を見る
10段の階段を1段ずつ、または2段ずつ、また1段と2段を混ぜて上るとき、全部で何通りの上り方がありますか。
【小4算数】垂直と平行、台形と平行四辺形 小4算数基礎講座 第12回

単元:
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題
指導講師:
こばちゃん塾
問題文全文(内容文):
・下の図で、直線㋐、直線㋑、直線㋒は平行です。角㋓、角㋔の大きさは何度ですか。
・下の図で、直線㋐、直線㋑は平行です。角㋒、角㋓の大きさは何度ですか。
・下の図で、直線㋐と垂直になっている直線はどれですか。また、直線㋑と平行になっている直線はどれですか。
・下の図で、点Aを通って直線㋐に垂直な直線と平行な直線をかきましょう。
・下の四角形から、台形と平行四辺形を見つけましょう。
・下の図のように平行四辺形の紙を点線㋐で切り分けます。
①何という名前の四角形ができますか。
②できた四角形には、平行な辺の組は何組ありますか。
・下の平行四辺形で、辺AD、辺CDの長さは何㎝ですか。また、角A、角Dの大きさは何度ですか。
*図は動画内参照
この動画を見る
・下の図で、直線㋐、直線㋑、直線㋒は平行です。角㋓、角㋔の大きさは何度ですか。
・下の図で、直線㋐、直線㋑は平行です。角㋒、角㋓の大きさは何度ですか。
・下の図で、直線㋐と垂直になっている直線はどれですか。また、直線㋑と平行になっている直線はどれですか。
・下の図で、点Aを通って直線㋐に垂直な直線と平行な直線をかきましょう。
・下の四角形から、台形と平行四辺形を見つけましょう。
・下の図のように平行四辺形の紙を点線㋐で切り分けます。
①何という名前の四角形ができますか。
②できた四角形には、平行な辺の組は何組ありますか。
・下の平行四辺形で、辺AD、辺CDの長さは何㎝ですか。また、角A、角Dの大きさは何度ですか。
*図は動画内参照
【中学受験算数】階差数列の解き方!細かく説明!!【毎日1題中学受験算数37】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
こばちゃん塾
問題文全文(内容文):
4,6,9,13,18,24・・・の数列の20番目の数はいくつですか?
この動画を見る
4,6,9,13,18,24・・・の数列の20番目の数はいくつですか?
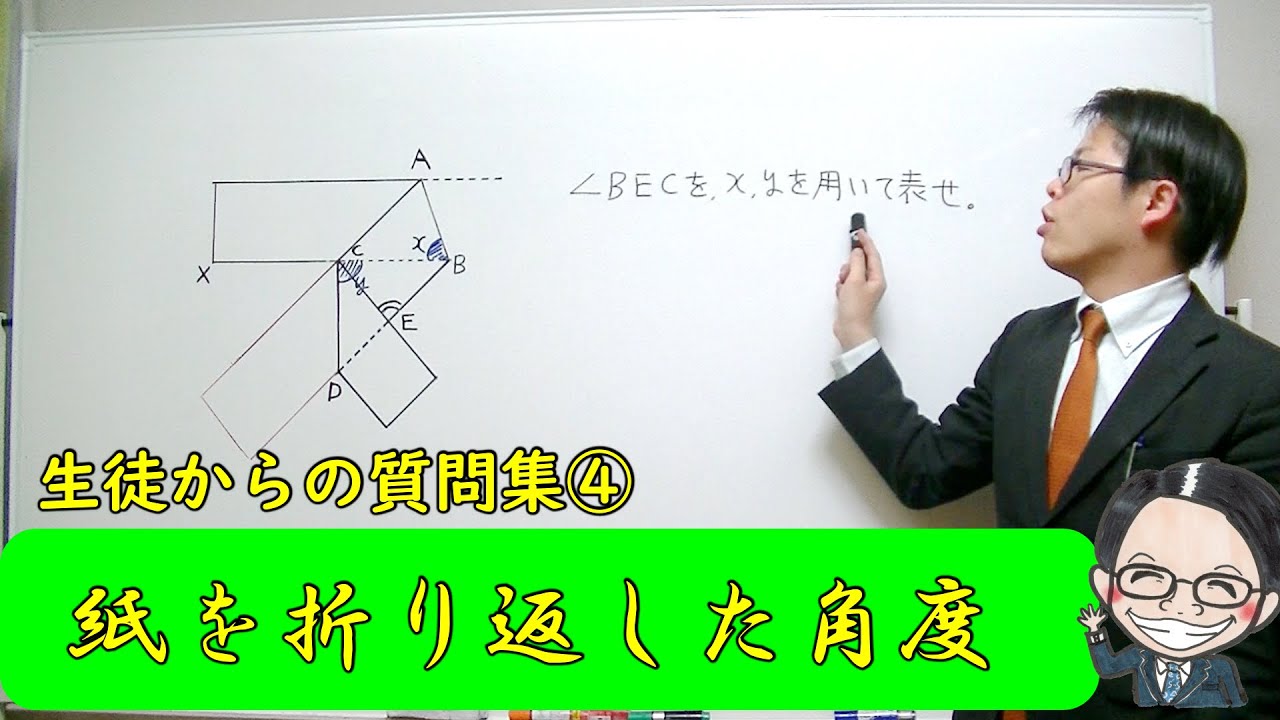
生徒からの質問4 紙を折り返した角度を他の角度で表す
【中学受験算数】この並び!あなたには規則が見破れますか!?【毎日1題中学受験算数36】
単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
こばちゃん塾
問題文全文(内容文):
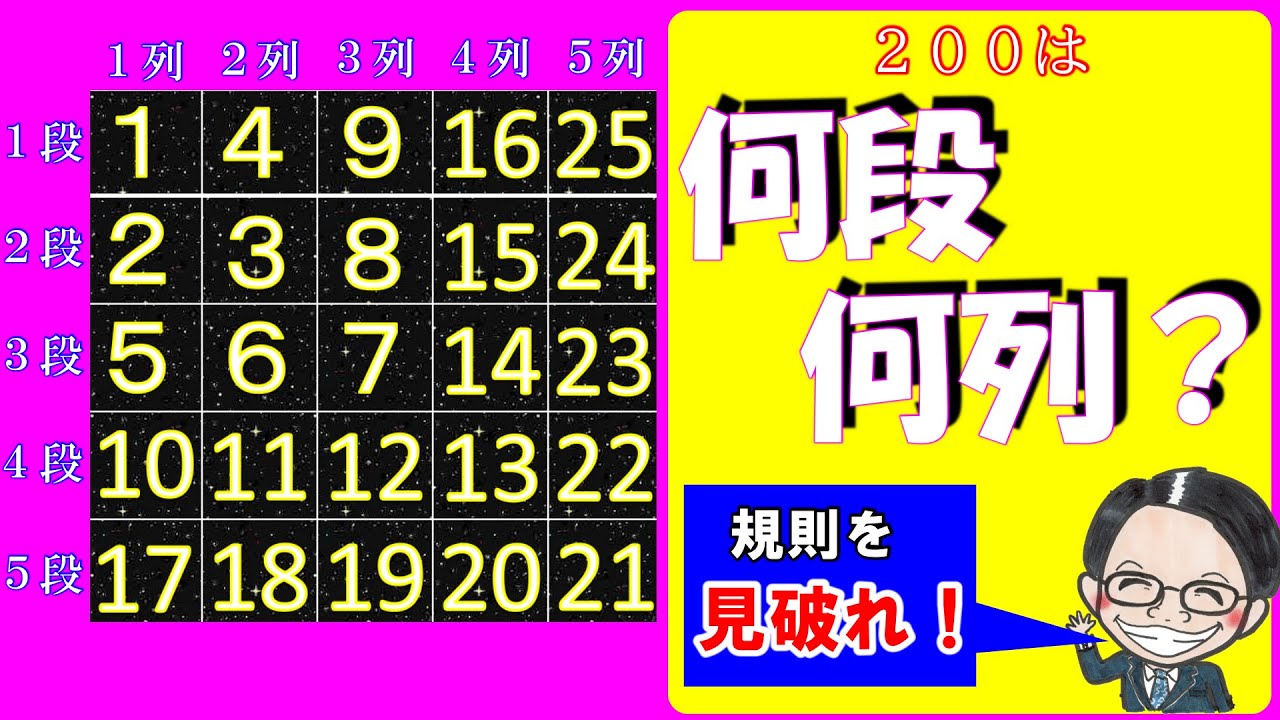
下の表はあるきまりにしたがって、1からの整数を並べたものです。
200は何段の何列ですか。
*表は動画内参照
この動画を見る
下の表はあるきまりにしたがって、1からの整数を並べたものです。
200は何段の何列ですか。
*表は動画内参照
【小4算数】垂直と平行の仕組みと書き方を知ろう! 小4算数基礎講座 第11回

単元:
#算数(中学受験)#平面図形#角度と面積#平面図形その他
指導講師:
こばちゃん塾
問題文全文(内容文):
・下の図で、直線㋐に垂直な直線はどれですか。
・下の図で平行になっている直線はどれとどれですか。
・下の図で直線㋓に平行な直線はどれですか。
すべて答えましょう。
・点Aを通って直線㋐に垂直な直線をかきましょう。
・点Aを通って、直線㋐に平行な直線をかきましょう。
*図は動画内参照
この動画を見る
・下の図で、直線㋐に垂直な直線はどれですか。
・下の図で平行になっている直線はどれとどれですか。
・下の図で直線㋓に平行な直線はどれですか。
すべて答えましょう。
・点Aを通って直線㋐に垂直な直線をかきましょう。
・点Aを通って、直線㋐に平行な直線をかきましょう。
*図は動画内参照
【中学受験算数】驚きのルールを見破れ!パスカルの三角形!!【毎日1題中学受験算数35】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
こばちゃん塾
問題文全文(内容文):
下の数の列はある規則にしたがって並んでいます。
12段目の数の和はいくつですか。
*図は動画内参照
この動画を見る
下の数の列はある規則にしたがって並んでいます。
12段目の数の和はいくつですか。
*図は動画内参照
【小4算数】大きな数 億と兆② 大きな数のしくみと計算を知ろう! 小4算数基礎講座 第10回

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
こばちゃん塾
問題文全文(内容文):
・4600億について、次の数を答えましょう。
①10倍した数 ②100倍した数 ③10でわった数 ④100でわった数
・12兆について、次の数をかきましょう。
①10倍した数
②100倍した数
③10でわった数
④100でわった数
・29×34=986を使って、2900×3400を求めましょう。
・47×18=846を使って、答えを求めましょう。
①470×1800=846
②47万×18億=846
・319×254の計算を筆算でしましょう。
・次の計算を筆算でしましょう。
①
$\begin{array}{r}
216 \\[-3pt]
\underline{\times\phantom{0}445}\\[-3pt]
\end{array}$
②
$\begin{array}{r}
97 \\[-3pt]
\underline{\times\phantom{0}364}\\[-3pt]
\end{array}$
③
$\begin{array}{r}
538 \\[-3pt]
\underline{\times\phantom{0}106}\\[-3pt]
\end{array}$
この動画を見る
・4600億について、次の数を答えましょう。
①10倍した数 ②100倍した数 ③10でわった数 ④100でわった数
・12兆について、次の数をかきましょう。
①10倍した数
②100倍した数
③10でわった数
④100でわった数
・29×34=986を使って、2900×3400を求めましょう。
・47×18=846を使って、答えを求めましょう。
①470×1800=846
②47万×18億=846
・319×254の計算を筆算でしましょう。
・次の計算を筆算でしましょう。
①
$\begin{array}{r}
216 \\[-3pt]
\underline{\times\phantom{0}445}\\[-3pt]
\end{array}$
②
$\begin{array}{r}
97 \\[-3pt]
\underline{\times\phantom{0}364}\\[-3pt]
\end{array}$
③
$\begin{array}{r}
538 \\[-3pt]
\underline{\times\phantom{0}106}\\[-3pt]
\end{array}$
【中学受験算数】等差数列の和!実は一瞬で解けます!!【毎日1題中学受験算数34】

単元:
#算数(中学受験)#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
こばちゃん塾
問題文全文(内容文):
135,133,131,129,127・・・と並んでいる数の並びがあります。
26番目までの数をすべて足すといくつになりますか。
この動画を見る
135,133,131,129,127・・・と並んでいる数の並びがあります。
26番目までの数をすべて足すといくつになりますか。
【中学受験算数】超便利技!三角数ってなんだろう!?公式の成り立ちもスッキリ解説!【毎日1題中学受験算数33(番外編)】

単元:
#算数(中学受験)#平面図形#平面図形その他
指導講師:
こばちゃん塾
問題文全文(内容文):
$(n番目の三角数)=(1+n)\times n \div 2$
が成り立つ理由の解説。
この動画を見る
$(n番目の三角数)=(1+n)\times n \div 2$
が成り立つ理由の解説。
【中学受験算数】三角数公式で瞬殺!?図形の枚数を求めよう!【毎日1題中学受験算数32】

単元:
#算数(中学受験)#平面図形#平面図形その他
指導講師:
こばちゃん塾
問題文全文(内容文):
1辺が1㎝の正方形を使って下図のような図形を作ります。
12番目の図形を作るには正方形が何個必要ですか。
*図は動画内参照
この動画を見る
1辺が1㎝の正方形を使って下図のような図形を作ります。
12番目の図形を作るには正方形が何個必要ですか。
*図は動画内参照
【最新】【高校入試】令和2年度 岡山県立高校入試(数学)を元大手塾講師が全問解説します!!

単元:
#数学(中学生)#高校入試過去問(数学)#岡山県公立高校入試
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣
①4+(-8)=
②(-18)÷(-3)=
③4(2a-b)-(-3a+b)=
④$6ab×(-\frac{3}{2}a)=$
⑤$(1-\sqrt 5)^2=$
⑥$x^2-x-3=$
⑦*図は動画内参照
⑧3枚の硬貨を同時に投げるとき、少なくとも1枚は表となる確率
⑨この円柱の体積は球の体積の▢倍
ア$\frac{3}{2}$ イ$\frac{4}{3}$ ウ$\frac{5}{4}$ エ$\frac{6}{5}$
⑩
1⃣右の度数分布表は、ある中学校のバスケットボール部が行った15試合の練習試合について,1試合ごとの得点の記録を整理したものである。
(1),(2)を求めなさい。
(1) 80点以上100点未満の階級の相対度数
(2) 度数分布表からわかる得点の平均値
2⃣
大輝さんと桃子さんは,町内会の夏祭りでボールすくいを計画している。2人は,
町内会の人から模様入りと単色の2種類のボールが合計500個入っている袋を1つ
受け取った。その人に聞いてみたところ、ボール500個の消費税込みの価格は
2,000円であることがわかった。2人は、袋の中に入っている模様入りボールと
単色ボールの個数を調べる方法について,次のように考えた。1,2に答えなさい
ただし、ボールの大きさは、すべて同じものとする。
「大輝さんの考え」
標本調査を行えばそれぞれのおよその個数がわかる
「桃子さんの考え」
それぞれのボールの1個あたりの価格がわかれば、連立方程式を利用して、それぞれの正確な個数を求めることができる。
①大輝さんがこの袋の中から25個のポールを無作為に抽出したところ,抽出した
ボ一ルのうち模様入りボールは6個だった。はじめに袋の中に入っていた模様入りボールのおよその個数として最も適当なのは、アーエのうちではどれですか。一つ答えなさい。
ア およそ100個
イ およそ120個
ウ およそ140個
工 およそ160個
②桃子さんが調べたところ,消費税込みの価格で模様入りボールは1個7円,単色
ボールは1個3円であることがわかった。(1),(2)に答えなさい。
(1) 模様入りボールをx個,単色ボールをy個として、連立方程式をつくりなさい。
(2)ボール500個のうち、模様入りボールと単色ボールをそれぞれ何個ずつあるかを求めなさい。
3⃣
①変化の割合が正になるのは、ア~エのうちではどれですか。当てはまるものをすべて答えなさい。
ア 関数y=2xで,xの値が0から4まで増加するとき。
イ 関数y=-3x+4で、xの値が1から3まで増加するとき。
ウ 関数$y=\frac{6}{x}$の値が3から6まで増加するとき。
エ 関数$y=-x^2$で、xの値が-3から1まで増加するとき。
②aの値は,次のように求めることができる。$\fbox{ (1) }$には適当な式を書きなさい。ただし、$\fbox{ (2) }$は答えを求めるまでの過程も書きなさい。
関数$y=ax^2$について,x =- 2のとき,y=4aである。
また、x=4のとき、y=$\fbox{ (1) }$である。
よって,変化の割合について,$\fbox{ (2) }$
③点Cの座標は(▢、0)である。
④点Aからy軸にひいた垂線とy軸との交点をHとする。台形OHACを,直線OHを回転の軸として1回転させてできる立体の体積は$\fbox{ (1) }$㎤であり、表面積は$\fbox{ (2) }$㎠である。ただし,原点Oから点(1,0)までの距離,原点Oから点(0,1)までの距離をそれぞれ1cmとする。
4⃣
太郎さんは、道路側が斜めに切り取られたような建物を見て、興味をもち調べると、その建物は周辺の日当たりなどを確保するためのきまりにもとづいて建てられていることがわかった。そのきまりについて,次のように、真横から見た模式図をかいてまとめた。①~④に答えなさい。
太郎さんのまとめ1
直線lを平らな地面とみなす。また,2点O,Aは直線l上の点で、線分OAを道路とし,
線分OAの長さを道路の幅とみなす。
きまりⅠ
建物は,道路側に(直線ABから)はみ出さないようにする。
あわせて建物は,図1で,OA:AB=4:5となる直線OBを越えてはいけない。
きまりⅡ
建物は、きまりⅠにもとづいて建てなければならない。ただし、道路の幅が12m以上のときは、図2で,直線OBを越えてもよいが、OC=1.25×OA、OC:CD=2:3となる直線ODを越えてはいけない。これは、直線CDより道路から遠い部分に適用される。
【図1,2の説明】
・色のついた図形を建物とみなし,点Bは図1と図2の,点D、E、Hは図2の建物とみなす図形の周上の点
・点C,Gは、半直線OA上の点
・l⊥AB、 l⊥CD、l⊥GE
・点Eは、点Dを通り、直線lに平行な直線と直線OBの交点
・点Fは、直線ABと直線DEの交点
・点Hは、直線OEと直線CDの交点
① 点Aを通り,直線をに垂直な直線を定規とコンバスを使って作図しなさい。作図に使った線は残しておきなさい。
②図1において、OA=12mのとき、線分ABの長さを求めなさい。
③太郎さんは、道路の幅が12mできまりⅡが適用されたとき,図2をもとに図3を
作成し、点C,Dの特徴について考えた。$\fbox{ (1) }$、$\fbox{ (2) }$には適当な数または式を書きなさい。また、$\fbox{ (3) }$には点Eのx座標を求める過程の続きを書き、を完成させなさい。
図3のように,点Oを原点に,直線lをx軸にしたグラフを考える。
直線OBの式を$y=\frac{5}{4}x$とすると、
直線ODの式は$y=\fbox{ (1) }$である。
OA=12のとき、OC=1.25×OA=15となるので,点Aのx座標を12とすると、点C、Dのx座標はともに15である。
このとき、点Eのx座標を求める。
点D、Eのy座標はともに$\fbox{ (2) }$である。また、$\fbox{ (3) }$である。
よって線分ACと線分CGの長さが等しいので、AC:CG=1:1である。
つまり、点Cは線分AGの中点であり、点Dは線分FEの中点である。
④太郎さんは、③の図3をもとに図4を作成し、建物Xと道路をはさんで向かいあう建物Yの壁面にできる建物Xの影について考えた。▢に適当な数を書き、を完成させなさい。
図4について、点Pは,点Fを通り直線ODに平行な直線とy軸との交点とする。
道路の幅(線分OAの長さ)が12mのとき,きまりⅠ,Ⅱの制限いっぱいに建てられた建物Xの影の部分が,ちょうど道路の幅と同じになるときを考える。南中高度で調べると,春分·秋分の日のころだとわかった。太陽の光線は平行に進むと考えることができるので,直線ODと直線PFを太陽の光線とみなすことにする。
このとき,線分OPはきまりⅠが適用されていない場合に,建物Yの壁面にできる影
の部分とみなすことができる。
よって,きまりⅠが適用されていない場合,線分OPの長さが▢mであることより、建物Yの壁面にできる影の部分は、この高さまであるとわかる。
きまりによって,建物Yの日当たりがより確保されていることがわかった。
5⃣次の図のように、∠DABが角の平行四近形ABCDについて、線分ADを2:1に分ける点をEとする。線分A,Bの延長線上に、点Aとは異なる点FをAB=BFとなるようにとり、点Bと点F、点Eと点Fをそれぞれ結ぶ。線分EFと線分BCの交点をG、線分EFと平行四辺形ABCDの対角線BDの交点をHとする。また、点Hから線分ADにひいた垂線と線分ADとの交点をPとする。
①,②は指示に従って答えなさい。③は▢に適当な数を書きなさい。
①四角形が平行四辺形にならない場合があるのは、ア~エのうちではどれですか。一つ答えなさい。
ア 1組の向かい合う辺が長さが等しくて平行であるとき。
イ 2本の対角線が、それぞれの中点で交わるとき。
ウ 2本の対角線が、長をが等しくて垂直に交わるとき。
工 2組の向かいあう角が、それぞれ等しいとき。
②BG=EDは、次のように導くことができる。$y=\fbox{ (1) }$には、△AFE∽△BFGの証明の過程を書きなさい。また,$y=\fbox{ (2) }$には適当な教を書きなさい。
△AFEと△BFGにおいて,$\fbox{ (1) }$
△AFE∽△BFGである。
よって、この結果より,BG=$\fbox{ (2) }$AE となるので、BG=ED である。
③ AD=15cm,DH=EH,△BFGの面積が20$\sqrt 6$㎠のとき、線分HPの長さは$\fbox{ (1) }$㎝ であり、線分ABの長さは$\fbox{ (2) }$㎝である。
*図は動画内参照
この動画を見る
1⃣
①4+(-8)=
②(-18)÷(-3)=
③4(2a-b)-(-3a+b)=
④$6ab×(-\frac{3}{2}a)=$
⑤$(1-\sqrt 5)^2=$
⑥$x^2-x-3=$
⑦*図は動画内参照
⑧3枚の硬貨を同時に投げるとき、少なくとも1枚は表となる確率
⑨この円柱の体積は球の体積の▢倍
ア$\frac{3}{2}$ イ$\frac{4}{3}$ ウ$\frac{5}{4}$ エ$\frac{6}{5}$
⑩
1⃣右の度数分布表は、ある中学校のバスケットボール部が行った15試合の練習試合について,1試合ごとの得点の記録を整理したものである。
(1),(2)を求めなさい。
(1) 80点以上100点未満の階級の相対度数
(2) 度数分布表からわかる得点の平均値
2⃣
大輝さんと桃子さんは,町内会の夏祭りでボールすくいを計画している。2人は,
町内会の人から模様入りと単色の2種類のボールが合計500個入っている袋を1つ
受け取った。その人に聞いてみたところ、ボール500個の消費税込みの価格は
2,000円であることがわかった。2人は、袋の中に入っている模様入りボールと
単色ボールの個数を調べる方法について,次のように考えた。1,2に答えなさい
ただし、ボールの大きさは、すべて同じものとする。
「大輝さんの考え」
標本調査を行えばそれぞれのおよその個数がわかる
「桃子さんの考え」
それぞれのボールの1個あたりの価格がわかれば、連立方程式を利用して、それぞれの正確な個数を求めることができる。
①大輝さんがこの袋の中から25個のポールを無作為に抽出したところ,抽出した
ボ一ルのうち模様入りボールは6個だった。はじめに袋の中に入っていた模様入りボールのおよその個数として最も適当なのは、アーエのうちではどれですか。一つ答えなさい。
ア およそ100個
イ およそ120個
ウ およそ140個
工 およそ160個
②桃子さんが調べたところ,消費税込みの価格で模様入りボールは1個7円,単色
ボールは1個3円であることがわかった。(1),(2)に答えなさい。
(1) 模様入りボールをx個,単色ボールをy個として、連立方程式をつくりなさい。
(2)ボール500個のうち、模様入りボールと単色ボールをそれぞれ何個ずつあるかを求めなさい。
3⃣
①変化の割合が正になるのは、ア~エのうちではどれですか。当てはまるものをすべて答えなさい。
ア 関数y=2xで,xの値が0から4まで増加するとき。
イ 関数y=-3x+4で、xの値が1から3まで増加するとき。
ウ 関数$y=\frac{6}{x}$の値が3から6まで増加するとき。
エ 関数$y=-x^2$で、xの値が-3から1まで増加するとき。
②aの値は,次のように求めることができる。$\fbox{ (1) }$には適当な式を書きなさい。ただし、$\fbox{ (2) }$は答えを求めるまでの過程も書きなさい。
関数$y=ax^2$について,x =- 2のとき,y=4aである。
また、x=4のとき、y=$\fbox{ (1) }$である。
よって,変化の割合について,$\fbox{ (2) }$
③点Cの座標は(▢、0)である。
④点Aからy軸にひいた垂線とy軸との交点をHとする。台形OHACを,直線OHを回転の軸として1回転させてできる立体の体積は$\fbox{ (1) }$㎤であり、表面積は$\fbox{ (2) }$㎠である。ただし,原点Oから点(1,0)までの距離,原点Oから点(0,1)までの距離をそれぞれ1cmとする。
4⃣
太郎さんは、道路側が斜めに切り取られたような建物を見て、興味をもち調べると、その建物は周辺の日当たりなどを確保するためのきまりにもとづいて建てられていることがわかった。そのきまりについて,次のように、真横から見た模式図をかいてまとめた。①~④に答えなさい。
太郎さんのまとめ1
直線lを平らな地面とみなす。また,2点O,Aは直線l上の点で、線分OAを道路とし,
線分OAの長さを道路の幅とみなす。
きまりⅠ
建物は,道路側に(直線ABから)はみ出さないようにする。
あわせて建物は,図1で,OA:AB=4:5となる直線OBを越えてはいけない。
きまりⅡ
建物は、きまりⅠにもとづいて建てなければならない。ただし、道路の幅が12m以上のときは、図2で,直線OBを越えてもよいが、OC=1.25×OA、OC:CD=2:3となる直線ODを越えてはいけない。これは、直線CDより道路から遠い部分に適用される。
【図1,2の説明】
・色のついた図形を建物とみなし,点Bは図1と図2の,点D、E、Hは図2の建物とみなす図形の周上の点
・点C,Gは、半直線OA上の点
・l⊥AB、 l⊥CD、l⊥GE
・点Eは、点Dを通り、直線lに平行な直線と直線OBの交点
・点Fは、直線ABと直線DEの交点
・点Hは、直線OEと直線CDの交点
① 点Aを通り,直線をに垂直な直線を定規とコンバスを使って作図しなさい。作図に使った線は残しておきなさい。
②図1において、OA=12mのとき、線分ABの長さを求めなさい。
③太郎さんは、道路の幅が12mできまりⅡが適用されたとき,図2をもとに図3を
作成し、点C,Dの特徴について考えた。$\fbox{ (1) }$、$\fbox{ (2) }$には適当な数または式を書きなさい。また、$\fbox{ (3) }$には点Eのx座標を求める過程の続きを書き、を完成させなさい。
図3のように,点Oを原点に,直線lをx軸にしたグラフを考える。
直線OBの式を$y=\frac{5}{4}x$とすると、
直線ODの式は$y=\fbox{ (1) }$である。
OA=12のとき、OC=1.25×OA=15となるので,点Aのx座標を12とすると、点C、Dのx座標はともに15である。
このとき、点Eのx座標を求める。
点D、Eのy座標はともに$\fbox{ (2) }$である。また、$\fbox{ (3) }$である。
よって線分ACと線分CGの長さが等しいので、AC:CG=1:1である。
つまり、点Cは線分AGの中点であり、点Dは線分FEの中点である。
④太郎さんは、③の図3をもとに図4を作成し、建物Xと道路をはさんで向かいあう建物Yの壁面にできる建物Xの影について考えた。▢に適当な数を書き、を完成させなさい。
図4について、点Pは,点Fを通り直線ODに平行な直線とy軸との交点とする。
道路の幅(線分OAの長さ)が12mのとき,きまりⅠ,Ⅱの制限いっぱいに建てられた建物Xの影の部分が,ちょうど道路の幅と同じになるときを考える。南中高度で調べると,春分·秋分の日のころだとわかった。太陽の光線は平行に進むと考えることができるので,直線ODと直線PFを太陽の光線とみなすことにする。
このとき,線分OPはきまりⅠが適用されていない場合に,建物Yの壁面にできる影
の部分とみなすことができる。
よって,きまりⅠが適用されていない場合,線分OPの長さが▢mであることより、建物Yの壁面にできる影の部分は、この高さまであるとわかる。
きまりによって,建物Yの日当たりがより確保されていることがわかった。
5⃣次の図のように、∠DABが角の平行四近形ABCDについて、線分ADを2:1に分ける点をEとする。線分A,Bの延長線上に、点Aとは異なる点FをAB=BFとなるようにとり、点Bと点F、点Eと点Fをそれぞれ結ぶ。線分EFと線分BCの交点をG、線分EFと平行四辺形ABCDの対角線BDの交点をHとする。また、点Hから線分ADにひいた垂線と線分ADとの交点をPとする。
①,②は指示に従って答えなさい。③は▢に適当な数を書きなさい。
①四角形が平行四辺形にならない場合があるのは、ア~エのうちではどれですか。一つ答えなさい。
ア 1組の向かい合う辺が長さが等しくて平行であるとき。
イ 2本の対角線が、それぞれの中点で交わるとき。
ウ 2本の対角線が、長をが等しくて垂直に交わるとき。
工 2組の向かいあう角が、それぞれ等しいとき。
②BG=EDは、次のように導くことができる。$y=\fbox{ (1) }$には、△AFE∽△BFGの証明の過程を書きなさい。また,$y=\fbox{ (2) }$には適当な教を書きなさい。
△AFEと△BFGにおいて,$\fbox{ (1) }$
△AFE∽△BFGである。
よって、この結果より,BG=$\fbox{ (2) }$AE となるので、BG=ED である。
③ AD=15cm,DH=EH,△BFGの面積が20$\sqrt 6$㎠のとき、線分HPの長さは$\fbox{ (1) }$㎝ であり、線分ABの長さは$\fbox{ (2) }$㎝である。
*図は動画内参照
【中学受験算数】さあ!当てはまる整数を当てよう!出来るかな?【毎日1題中学受験算数31】

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題
指導講師:
こばちゃん塾
問題文全文(内容文):
150×A=B×Bの式を満たす0でない整数A,Bがあります。
Bが最も小さいとき、AとBの値を求めましょう。
この動画を見る
150×A=B×Bの式を満たす0でない整数A,Bがあります。
Bが最も小さいとき、AとBの値を求めましょう。
【中学受験算数】約数はいくつ?数えなくても出来るんです!【毎日1題中学受験算数30】

【中学受験算数】面積だけで体積が分かるって本当!?見たあとにスッキリできる必殺テクニック紹介!【毎日1題中学受験算数29】

単元:
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師:
こばちゃん塾
問題文全文(内容文):
下の直方体の㋐の面積が48㎠、㋑が72㎠、㋒は96㎠です。
この直方体の体積は何㎤ですか。
*図は動画内参照
この動画を見る
下の直方体の㋐の面積が48㎠、㋑が72㎠、㋒は96㎠です。
この直方体の体積は何㎤ですか。
*図は動画内参照
【小4算数】大きな数 億と兆① 大きな数ってワクワクするよね! 小4算数基礎講座 第9回

単元:
#算数(中学受験)#計算と数の性質#数の性質その他
指導講師:
こばちゃん塾
問題文全文(内容文):
例題
・次の数のよみ方を漢字でかきましょう。
①431815176
②826543007000
1⃣次のよみ方を漢字でかきましょう。
154238000602200
2⃣次の数を数字でかきましょう。
①十二兆三千三十九億
②10億を260こ集めた数
・下の12まいのカードをならべてできる12けたの整数のうち、いちばん大きい数といちばん小さいか数をかきましょう。
$\fbox{ 0 }$$\fbox{ 0 }$$\fbox{ 0 }$$\fbox{ 1 }$$\fbox{ 2 }$$\fbox{ 3 }$$\fbox{ 4 }$$\fbox{ 5 }$$\fbox{ 6 }$$\fbox{ 7 }$$\fbox{ 8 }$
・0,1,2,3の4この数字を使ってできる整数のうち、一兆の位が1になる数で、いちばん大きい数をつくりましょう。
この動画を見る
例題
・次の数のよみ方を漢字でかきましょう。
①431815176
②826543007000
1⃣次のよみ方を漢字でかきましょう。
154238000602200
2⃣次の数を数字でかきましょう。
①十二兆三千三十九億
②10億を260こ集めた数
・下の12まいのカードをならべてできる12けたの整数のうち、いちばん大きい数といちばん小さいか数をかきましょう。
$\fbox{ 0 }$$\fbox{ 0 }$$\fbox{ 0 }$$\fbox{ 1 }$$\fbox{ 2 }$$\fbox{ 3 }$$\fbox{ 4 }$$\fbox{ 5 }$$\fbox{ 6 }$$\fbox{ 7 }$$\fbox{ 8 }$
・0,1,2,3の4この数字を使ってできる整数のうち、一兆の位が1になる数で、いちばん大きい数をつくりましょう。
【小4算数】大きな数 億と兆① 大きな数ってワクワクするよね! 小4算数基礎講座 第9回

単元:
#算数(中学受験)#計算と数の性質#数の性質その他
指導講師:
こばちゃん塾
問題文全文(内容文):
例題
1⃣次のよみ方を漢字でかきましょう。
154238000602200
2⃣次の数を数字でかきましょう
①十二兆三千三十九億
②10億を260こ集めた数
3⃣下の12まいのカードをならべてできる12けたの整数のうち、いちばん大きい数といちばん小さい数をかきましょう。
$\fbox{0}\fbox{0}\fbox{0}\fbox{1}\fbox{2}\fbox{3}\fbox{4}\fbox{5}\fbox{6}\fbox{7}\fbox{8}\fbox{9}$
4⃣0,1,2,3の4この数字を使ってできる整数のうち、一兆の位が1になる数で、いちばん大きい数をつくりましょう。
この動画を見る
例題
1⃣次のよみ方を漢字でかきましょう。
154238000602200
2⃣次の数を数字でかきましょう
①十二兆三千三十九億
②10億を260こ集めた数
3⃣下の12まいのカードをならべてできる12けたの整数のうち、いちばん大きい数といちばん小さい数をかきましょう。
$\fbox{0}\fbox{0}\fbox{0}\fbox{1}\fbox{2}\fbox{3}\fbox{4}\fbox{5}\fbox{6}\fbox{7}\fbox{8}\fbox{9}$
4⃣0,1,2,3の4この数字を使ってできる整数のうち、一兆の位が1になる数で、いちばん大きい数をつくりましょう。
【中学受験算数】1から50まで掛け算すると0はいくつ付くの?やり方が分かれば楽勝です!【毎日1題中学受験算数28】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
こばちゃん塾
問題文全文(内容文):
1から50までの整数をすべてかけあわせると、その答えには終わりに0がいくつ並びますか。
この動画を見る
1から50までの整数をすべてかけあわせると、その答えには終わりに0がいくつ並びますか。




