 ますただ
ますただ
 ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
距離空間(X,d)の部分集合Aの内部(Int A)の性質

単元:
#その他
指導講師:
ますただ
問題文全文(内容文):
(1)
$U_{\lambda\epsilon\Lambda}IntA_{\lambda} \subset Int( \subset _{\lambda\epsilon\Lambda}A_{\lambda})$を示せ
(2)
$U_{\lambda\epsilon\Lambda}IntA_{\lambda} = Int( \subset _{\lambda\epsilon\Lambda}A_{\lambda})$が成り立つか調べよ
この動画を見る
(1)
$U_{\lambda\epsilon\Lambda}IntA_{\lambda} \subset Int( \subset _{\lambda\epsilon\Lambda}A_{\lambda})$を示せ
(2)
$U_{\lambda\epsilon\Lambda}IntA_{\lambda} = Int( \subset _{\lambda\epsilon\Lambda}A_{\lambda})$が成り立つか調べよ
距離空間(X,d)はハウスドルフ空間であることを示してみた。

距離空間(X,d)の部分集合A={x ∊ X| d(x,a)>ε} (a∊X:fix)がXの開集合であることを示してみた

単元:
#その他
指導講師:
ますただ
問題文全文(内容文):
$(X,d):metric$
${}^{ \forall } a \in x,\ {}^{ \forall } e \gt 0$
$A=\{x \in x|d(x,a) \gt e\}$
このとき$A:open\ in\ x$を示せ
この動画を見る
$(X,d):metric$
${}^{ \forall } a \in x,\ {}^{ \forall } e \gt 0$
$A=\{x \in x|d(x,a) \gt e\}$
このとき$A:open\ in\ x$を示せ
大学入試問題#426「基本的な計算問題」 Instagram #三角関数
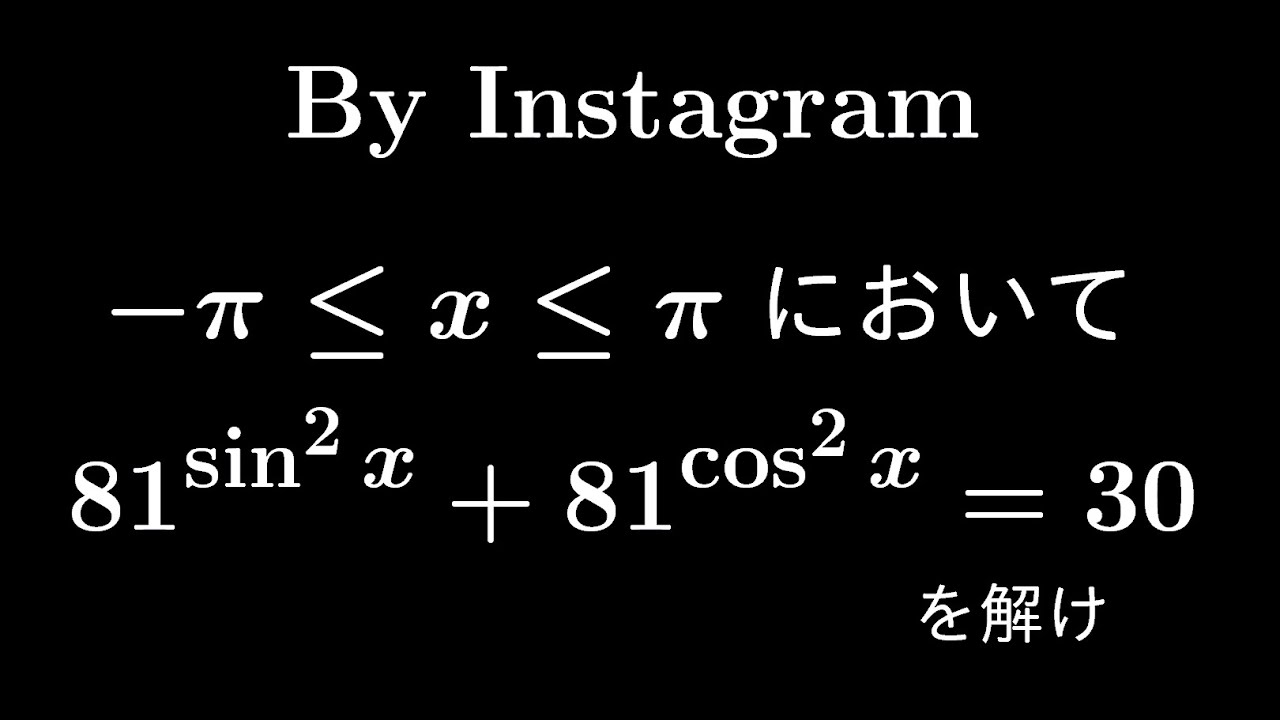
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$-\pi \leqq x \lt \pi$とする。
$81^{\sin^2x}+81^{\cos^2x}=30$
この動画を見る
$-\pi \leqq x \lt \pi$とする。
$81^{\sin^2x}+81^{\cos^2x}=30$
大学入試問題#425「これは要確認!」 奈良県立医科大学2014 #微積の応用

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{x} t\ f(x-t)dt=e^x-x-1$を満たす$f(x)$を求めよ
出典:2014年奈良県立医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{x} t\ f(x-t)dt=e^x-x-1$を満たす$f(x)$を求めよ
出典:2014年奈良県立医科大学 入試問題
大学入試問題#424「有名な極限!!」 鹿児島大学2018 #極限

単元:
#関数と極限#関数の極限#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)
$e^t \gt \displaystyle \frac{t^2}{2}(t \gt 0)$を示せ
(2)
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{log(x+1)}{x+1}$
出典:2018年鹿児島大学 入試問題
この動画を見る
(1)
$e^t \gt \displaystyle \frac{t^2}{2}(t \gt 0)$を示せ
(2)
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{log(x+1)}{x+1}$
出典:2018年鹿児島大学 入試問題
大学入試問題#423「よくみる問題?」 自治医科大学(2020) #面積

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\sqrt{ \displaystyle \frac{x}{6} }+\sqrt{ \displaystyle \frac{y}{4} }=1$と$x$軸、$y$軸で囲まれた部分の面積を求めよ。
出典:2020年自治医科大学 入試問題
この動画を見る
$\sqrt{ \displaystyle \frac{x}{6} }+\sqrt{ \displaystyle \frac{y}{4} }=1$と$x$軸、$y$軸で囲まれた部分の面積を求めよ。
出典:2020年自治医科大学 入試問題
大学入試問題#422「基本性質を利用」 自治医科大学2016 #複素数

単元:
#数Ⅱ#複素数と方程式#複素数
指導講師:
ますただ
問題文全文(内容文):
$z$:複素数
$\displaystyle \sum_{k=0}^9 z^k=0$のとき
$\displaystyle \frac{|z-2|^2+|z+2|^2}{5}$の値を求めよ
出典:2016年自治医科大学 入試問題
この動画を見る
$z$:複素数
$\displaystyle \sum_{k=0}^9 z^k=0$のとき
$\displaystyle \frac{|z-2|^2+|z+2|^2}{5}$の値を求めよ
出典:2016年自治医科大学 入試問題
大学入試問題#419「複素数の基本的な性質を網羅!」 東海大学医学部2017 #複素数

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東海大学
指導講師:
ますただ
問題文全文(内容文):
$\alpha=\displaystyle \frac{2+\sqrt{ 5 }i}{3}$のとき
$27(1+\displaystyle \frac{1}{\alpha}+\displaystyle \frac{1}{\alpha^2}+\displaystyle \frac{1}{\alpha^3})$の値を求めよ
出典:2017年東海大学医学部 入試問題
この動画を見る
$\alpha=\displaystyle \frac{2+\sqrt{ 5 }i}{3}$のとき
$27(1+\displaystyle \frac{1}{\alpha}+\displaystyle \frac{1}{\alpha^2}+\displaystyle \frac{1}{\alpha^3})$の値を求めよ
出典:2017年東海大学医学部 入試問題
ハルハルさんの作成問題「たぶん名作だと思います。難易度は高め」 図形 三角比

単元:
#数Ⅰ#数Ⅱ#式と証明#図形と計量#三角比への応用(正弦・余弦・面積)#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\theta$:実数
3辺の長さが$2\sin\theta,\ 2\cos\theta,\ \displaystyle \frac{\tan\theta}{\sqrt{ 3 }}$の三角形が単位円に内接している。
この条件を満たしている三角形の面積をすべて求めよ。
この動画を見る
$\theta$:実数
3辺の長さが$2\sin\theta,\ 2\cos\theta,\ \displaystyle \frac{\tan\theta}{\sqrt{ 3 }}$の三角形が単位円に内接している。
この条件を満たしている三角形の面積をすべて求めよ。
大学入試問題#418「場合分けがめんどくさいだけの積分」 藤田保健衛生大学医学部2016 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2\pi} |x\ \sin(x-\displaystyle \frac{\pi}{2})| dx$
出典:2016年藤田保健衛生大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{2\pi} |x\ \sin(x-\displaystyle \frac{\pi}{2})| dx$
出典:2016年藤田保健衛生大学医学部 入試問題
大学入試問題#417「一度は経験しときたい問題」 藤田保健衛生大学医学部2016 #微分の応用

単元:
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$3^\pi \gt \pi^3$を示せ
$e \lt 3 \lt \pi$は利用してよい
出典:2016年藤田保健衛生大学医学部 入試問題
この動画を見る
$3^\pi \gt \pi^3$を示せ
$e \lt 3 \lt \pi$は利用してよい
出典:2016年藤田保健衛生大学医学部 入試問題
大学入試問題#416「工夫して計算」 早稲田大学2008 #式変形

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$x$:実数
$x^3+\displaystyle \frac{1}{x^3}=52$を満たすとき
$x^4+\displaystyle \frac{1}{x^4}$の値を求めよ
出典:2008年早稲田大学 入試問題
この動画を見る
$x$:実数
$x^3+\displaystyle \frac{1}{x^3}=52$を満たすとき
$x^4+\displaystyle \frac{1}{x^4}$の値を求めよ
出典:2008年早稲田大学 入試問題
大学入試問題#415「解法は何通りかありそう・・・」 兵庫県立大学2022 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#兵庫県立大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} (\displaystyle \frac{\sin3x}{\sin2x})^2 dx$
出典:2022年兵庫県立大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} (\displaystyle \frac{\sin3x}{\sin2x})^2 dx$
出典:2022年兵庫県立大学 入試問題
大学入試問題#414「手抜き極限」 自治医科大学(2017) #極限

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#自治医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{3\sin4x}{x+\sin\ x}$
出典:2017年自治医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{3\sin4x}{x+\sin\ x}$
出典:2017年自治医科大学 入試問題
大学入試問題#413「解き方は色々ありそうだけど・・ここは」 佐賀大学2016 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{3}{4}\pi} \displaystyle \frac{x}{\sin\ x} dx$
出典:2016年佐賀大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{3}{4}\pi} \displaystyle \frac{x}{\sin\ x} dx$
出典:2016年佐賀大学 入試問題
大学入試問題#412「よくみる積分!?」 自治医科大学2022 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#自治医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e^3} x^2(log\ x)^2\ dx$
出典:2022年自治医科大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e^3} x^2(log\ x)^2\ dx$
出典:2022年自治医科大学 入試問題
大学入試問題#411「私学の医学科は3乗根の極限がお好き?」 藤田医科大学2022 #極限

単元:
#関数と極限#関数の極限#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 8 } \displaystyle \frac{x^2-9x+8}{\sqrt[ 3 ]{ x }-2}$
出典:2022年藤田医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 8 } \displaystyle \frac{x^2-9x+8}{\sqrt[ 3 ]{ x }-2}$
出典:2022年藤田医科大学 入試問題
大学入試問題#410「爽やかな積分問題」 産業医科大学2017 #定積分

単元:
#積分とその応用#定積分#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{2}^{1} \sqrt{ -1+\displaystyle \frac{2}{x} }\ dx$
出典:2017年産業医科大学 入試問題
この動画を見る
$\displaystyle \int_{2}^{1} \sqrt{ -1+\displaystyle \frac{2}{x} }\ dx$
出典:2017年産業医科大学 入試問題
大学入試問題#409「3乗根の極限きた~~~」 産業医科大学2019 #極限
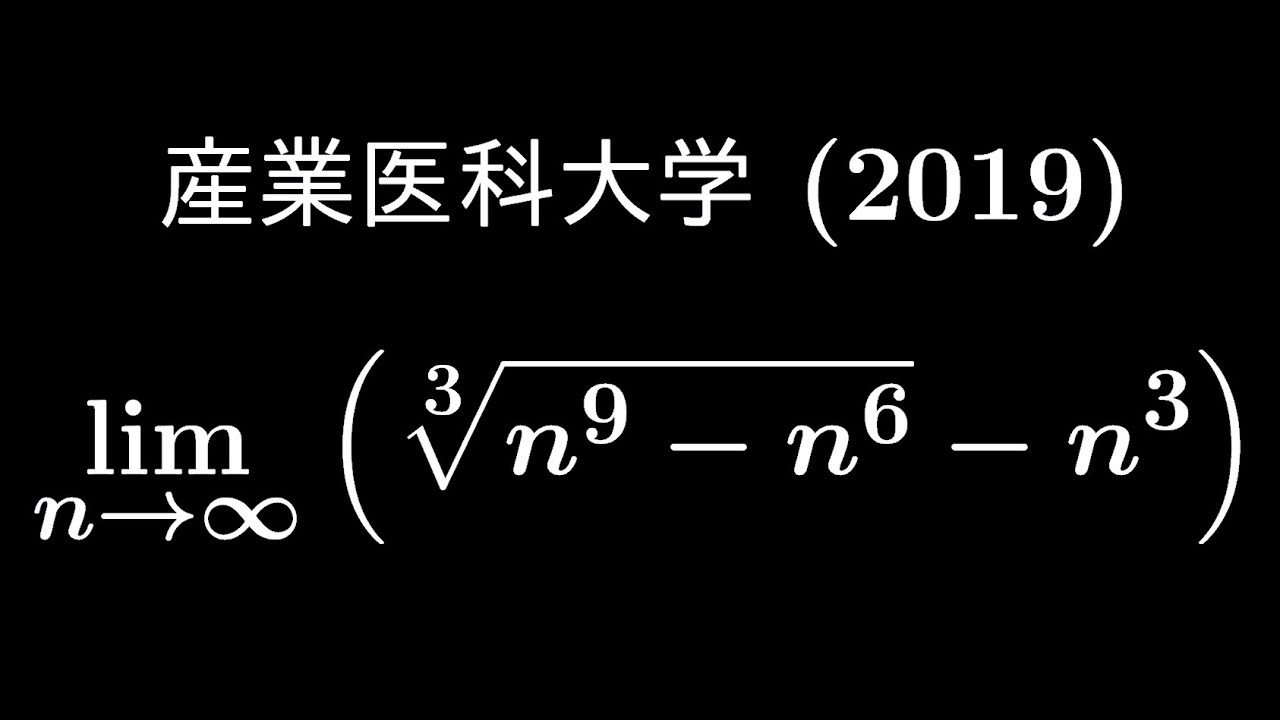
単元:
#関数と極限#関数の極限#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } (\sqrt[ 3 ]{ n^9-n^6 }-n^3)$
出典:2019年産業医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } (\sqrt[ 3 ]{ n^9-n^6 }-n^3)$
出典:2019年産業医科大学 入試問題
大学入試問題#408 産業医科大学(2018) #定積分

単元:
#関数と極限#積分とその応用#関数の極限#定積分#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{-1} \displaystyle \frac{x^2+2x+1}{\sqrt{ -x^2-2x+1 }} dx$
出典:2018年産業医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{-1} \displaystyle \frac{x^2+2x+1}{\sqrt{ -x^2-2x+1 }} dx$
出典:2018年産業医科大学 入試問題
奈良県教員採用試験「基本問題で良問!!」 #複素数

単元:
#複素数平面#複素数平面#その他#数学(高校生)#数C#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq \theta \lt 2\pi$
$|\cos\theta+i\sin\theta-3+i|$の最大値、最小値を求めよ
出典:奈良県教員採用試験
この動画を見る
$0 \leqq \theta \lt 2\pi$
$|\cos\theta+i\sin\theta-3+i|$の最大値、最小値を求めよ
出典:奈良県教員採用試験
大学入試問題#407「定石通り」 産業医科大学(2018) #極限

単元:
#関数と極限#関数の極限#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{x^2}{(3^x-1)\sin\ x}$
出典:2018年産業医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{x^2}{(3^x-1)\sin\ x}$
出典:2018年産業医科大学 入試問題
大学入試問題#406「(1)がなくて単発の出題だときつかった」 東京医科大学(2) 2022 #定積分

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \displaystyle \frac{\sqrt{ 4+5\tan|x| }}{1-\sin\ x}\ dx$
出典:2022年東京医科大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \displaystyle \frac{\sqrt{ 4+5\tan|x| }}{1-\sin\ x}\ dx$
出典:2022年東京医科大学 入試問題
大学入試問題#405「ロープをうまく通す」 東京医科大学 (1) 2022 #定積分

単元:
#積分とその応用#定積分#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \displaystyle \frac{dx}{\cos^2x\sqrt{ 9+7\tan|x| }}$
出典:2022年東京医科大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}} \displaystyle \frac{dx}{\cos^2x\sqrt{ 9+7\tan|x| }}$
出典:2022年東京医科大学 入試問題
ハルハルさんの積分問題(2) 「誘導があっても難問:コナミコマンドを使いたい!!↑↑↓↓←→←→BA」

単元:
#積分とその応用#定積分#その他
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\pi} \sqrt[ 3 ]{ \cos\displaystyle \frac{x}{6}+2\sin\displaystyle \frac{x}{3}-\cos\displaystyle \frac{x}{2} }\ dx$
この動画を見る
$\displaystyle \int_{0}^{\pi} \sqrt[ 3 ]{ \cos\displaystyle \frac{x}{6}+2\sin\displaystyle \frac{x}{3}-\cos\displaystyle \frac{x}{2} }\ dx$
根性のみで解く積分
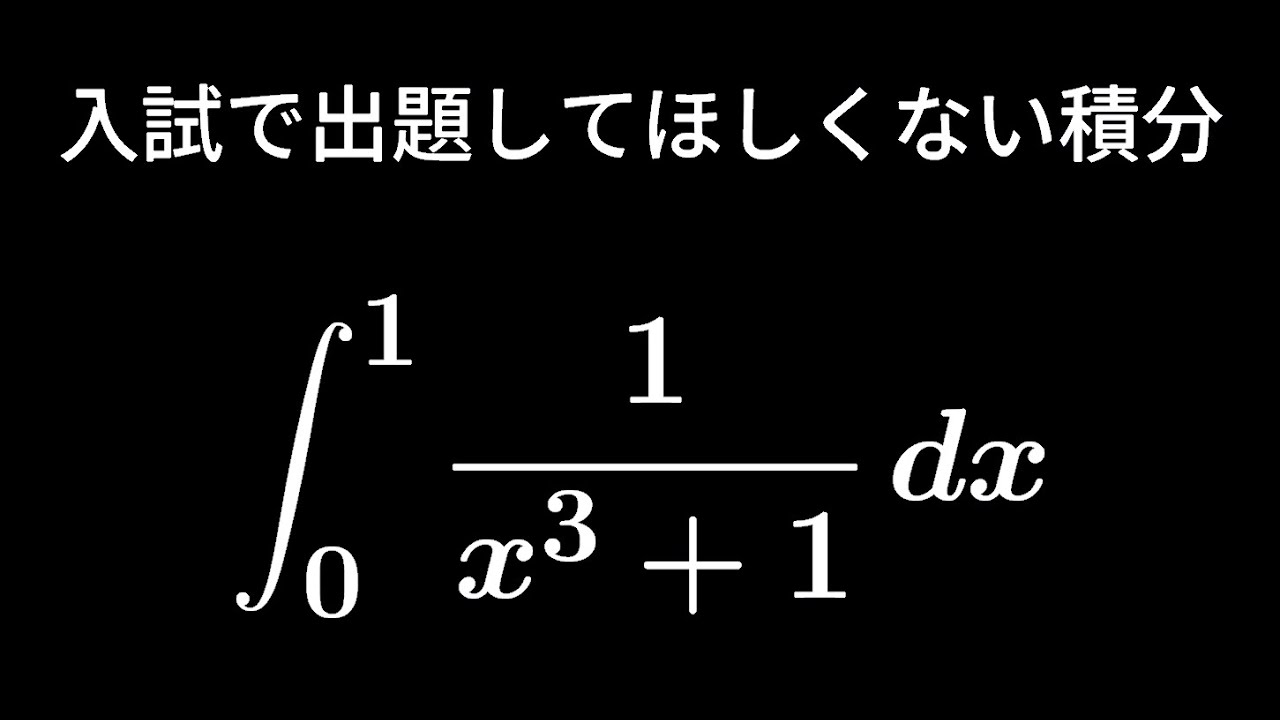
単元:
#積分とその応用#定積分#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{x^3+1} dx$
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{x^3+1} dx$
ハルハルさんの積分問題(1) 「大技の連打」 #定積分

単元:
#積分とその応用#定積分#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{x}{\sin\ x+\cos\ x+0.2} dx$
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{x}{\sin\ x+\cos\ x+0.2} dx$
大学入試問題#404「よく見る基本問題」 名古屋大学2009 #整数問題

単元:
#数A#整数の性質#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x,y$:正の実数
$\displaystyle \frac{2}{x}+\displaystyle \frac{1}{y}=\displaystyle \frac{1}{4}$をみたす組$(x,y)$をすべて求めよ。
出典:2009年名古屋大学 入試問題
この動画を見る
$x,y$:正の実数
$\displaystyle \frac{2}{x}+\displaystyle \frac{1}{y}=\displaystyle \frac{1}{4}$をみたす組$(x,y)$をすべて求めよ。
出典:2009年名古屋大学 入試問題
大学入試問題#403「教科書の例題にありそう」 東京電機大学2009 #定積分

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} x|3x-2| dx$
出典:2009年東京電機大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} x|3x-2| dx$
出典:2009年東京電機大学 入試問題



