 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【受験算数】えんぴつが48本、ボールペンが76本あります。これらを何人かの子どもに配ります。まず、えんぴつを全員に同じ本数ずつ、あまりがなるべく少なくなるように配りました…

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題
教材:
#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
えんぴつが48本、ボールペンが76本あります。これらを何人かの子どもに配ります。まず、えんぴつを全員に同じ本数ずつ、あまりがなるべく少なくなるように配りました。次に、ボールペンを全員に同じ本数ずつ、あまりがなるべく少なくなるように配りました。これについて、次の問いに答えなさい。
(1)もし、えんぴつが3本、ボールペンが1本余ったとすると、子どもの人数は何人ですか。考えられる人数のうち、最も少ない人数を答えなさい。
(2)もし、えんぴつとボールペンがどちらも1本以上あまり、あまったえんぴつの本数とあまったボールペンの本数が等しいとすると、子どもの人数は何人ですか。考えられる人数のうち、最も少ない人数を答えなさい。
この動画を見る
えんぴつが48本、ボールペンが76本あります。これらを何人かの子どもに配ります。まず、えんぴつを全員に同じ本数ずつ、あまりがなるべく少なくなるように配りました。次に、ボールペンを全員に同じ本数ずつ、あまりがなるべく少なくなるように配りました。これについて、次の問いに答えなさい。
(1)もし、えんぴつが3本、ボールペンが1本余ったとすると、子どもの人数は何人ですか。考えられる人数のうち、最も少ない人数を答えなさい。
(2)もし、えんぴつとボールペンがどちらも1本以上あまり、あまったえんぴつの本数とあまったボールペンの本数が等しいとすると、子どもの人数は何人ですか。考えられる人数のうち、最も少ない人数を答えなさい。
【高校物理】ブラッグ反射:波長1.5×10⁻¹⁰mのX線を,結晶の格子面に対してθの角度であてると,θ=30°のときに反射X線が強め合った。このとき,ブラックの反射条件の次数nは2であった。…

単元:
#物理#理科(高校生)#原子
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
波長1.5×10⁻¹⁰mのX線を,結晶の格子面に対してθの角度であてると,θ=30°のときに反射X線が強め合った。このとき,ブラックの反射条件の次数nは2であった。
(1)結晶の格子面の間隔はいくらか。
(2)強めあう反射X線と入射X線がなす角はいくらか。
この動画を見る
波長1.5×10⁻¹⁰mのX線を,結晶の格子面に対してθの角度であてると,θ=30°のときに反射X線が強め合った。このとき,ブラックの反射条件の次数nは2であった。
(1)結晶の格子面の間隔はいくらか。
(2)強めあう反射X線と入射X線がなす角はいくらか。
【受験算数】5をたすと8でわり切れ、1をひくと9でわり切れる整数について、次の問いに答えなさい。このような整数のうち、小さい方から5番目の整数はいくつですか。

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題
教材:
#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
5をたすと8でわり切れ、1をひくと9でわり切れる整数について、次の問いに答えなさい。
(1)このような整数のうち、小さい方から5番目の整数はいくつですか。
(2)このような整数のうち、2000に最も近い整数はいくつですか。
この動画を見る
5をたすと8でわり切れ、1をひくと9でわり切れる整数について、次の問いに答えなさい。
(1)このような整数のうち、小さい方から5番目の整数はいくつですか。
(2)このような整数のうち、2000に最も近い整数はいくつですか。
【数C】【空間ベクトル】平行六面体ABCD-EFGHにおいて、AC=a、AF=AF=b、AH=cとするとき、AGをa,b,cを用いて表せ

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
平行六面体 $\mathrm{ABCD}$-$\mathrm{EFGH}$において、
$\overrightarrow{\mathrm{AC}} = \vec{a},\overrightarrow{\mathrm{AF}} = \vec{b}, \overrightarrow{\mathrm{AH}} = \vec{c}$ とするとき、
$\overrightarrow{\mathrm{AG}} $ を $\vec{a}, \vec{b},\vec{c}$ を用いて表せ。
この動画を見る
平行六面体 $\mathrm{ABCD}$-$\mathrm{EFGH}$において、
$\overrightarrow{\mathrm{AC}} = \vec{a},\overrightarrow{\mathrm{AF}} = \vec{b}, \overrightarrow{\mathrm{AH}} = \vec{c}$ とするとき、
$\overrightarrow{\mathrm{AG}} $ を $\vec{a}, \vec{b},\vec{c}$ を用いて表せ。
【中学受験理科】水溶液の分類:下のア~力のいずれかの水溶液の入ったビーカー①〜⑥があります。どのビーカーにどの水溶液が入っているかを確かめるために次の実験を行いました。この実験をもとに、①~⑥のビー…

単元:
#理科(中学受験)#化学分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下のア~力のいずれかの水溶液の入ったビーカー①〜⑥があります。どのビーカーにどの水溶液が入っているかを確かめるために次の実験を行いました。この実験をもとに、①~⑥のビーカーに入っている水溶液を答えなさい。
水溶液
ア ホウ酸水
イ 酢酸水溶液
ウ 水酸化ナトリウム水溶液
エ 食塩水
オ アンモニア水
カ アルコール水溶液
実験1:それぞれのビーカーにBTB溶液を加えると、①③は緑色、②⑤は黄色,④⑥は青色に変化した。
実験2:電流を流してみると、①だけ流れなかった。
実験3:①②④にはにおいがあった。
実験4:水分を蒸発させると、①②④は何も残らず、③⑤⑥では白い固体が残った。
この動画を見る
下のア~力のいずれかの水溶液の入ったビーカー①〜⑥があります。どのビーカーにどの水溶液が入っているかを確かめるために次の実験を行いました。この実験をもとに、①~⑥のビーカーに入っている水溶液を答えなさい。
水溶液
ア ホウ酸水
イ 酢酸水溶液
ウ 水酸化ナトリウム水溶液
エ 食塩水
オ アンモニア水
カ アルコール水溶液
実験1:それぞれのビーカーにBTB溶液を加えると、①③は緑色、②⑤は黄色,④⑥は青色に変化した。
実験2:電流を流してみると、①だけ流れなかった。
実験3:①②④にはにおいがあった。
実験4:水分を蒸発させると、①②④は何も残らず、③⑤⑥では白い固体が残った。
【高校物理】阻止電圧:光電効果の実験で、光電管の陰極に振動数νの光をあて、光電流が0になるときの陰極に対する陽極の電位-VMを測定すると、図の関係が得られた。光電子は振動数がν0をこえたときにだけ飛…

単元:
#物理#理科(高校生)#原子
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
光電効果の実験で、光電管の陰極に振動数νの光をあて、光電流が0になるときの陰極に対する陽極の電位-VMを測定すると、図の関係が得られた。光電子は振動数がν0をこえたときにだけ飛び出す。電気素量をeとする。
(1) 振動数がν1の光をあてたとき、飛び出す光電子の運動エネルギーの最大値をV1を用いて表せ。
(2) プランク定数をhとして、仕事関数Wをh,ν0を用いて表せ。
(3) プランク定数hを,ν0,ν1,V1,eを用いて表せ
この動画を見る
光電効果の実験で、光電管の陰極に振動数νの光をあて、光電流が0になるときの陰極に対する陽極の電位-VMを測定すると、図の関係が得られた。光電子は振動数がν0をこえたときにだけ飛び出す。電気素量をeとする。
(1) 振動数がν1の光をあてたとき、飛び出す光電子の運動エネルギーの最大値をV1を用いて表せ。
(2) プランク定数をhとして、仕事関数Wをh,ν0を用いて表せ。
(3) プランク定数hを,ν0,ν1,V1,eを用いて表せ
【数Ⅲ】【積分とその応用】シュワルツの不等式{∫[a→b]f(x)g(x)dx}²≦(∫[a→b]{f(x)}²dx)(∫[a→b]{g(x)}²dx) を利用して、次の不等式が成り立つことを証明せよ

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
シュワルツの不等式
\[
\left\{ \int_a^b f(x)g(x) \, dx \right\}^2 \leq
\left( \int_a^b \{ f(x) \}^2 dx \right)
\left( \int_a^b \{ g(x) \}^2 dx \right) \quad (a < b)
\]
を利用して、\( 0 < a < b, \, h(x) > 0 \) のとき、次の不等式が成り立つことを証明せよ。
(1)
\[
(b - a)^2 < \int_a^b x^2 \, dx \int_a^b \frac{dx}{x^2}
\]
(2)
\[
(b - a)^2 \leq \int_a^b h(x) \, dx \int_a^b \frac{dx}{h(x)}
\]
この動画を見る
シュワルツの不等式
\[
\left\{ \int_a^b f(x)g(x) \, dx \right\}^2 \leq
\left( \int_a^b \{ f(x) \}^2 dx \right)
\left( \int_a^b \{ g(x) \}^2 dx \right) \quad (a < b)
\]
を利用して、\( 0 < a < b, \, h(x) > 0 \) のとき、次の不等式が成り立つことを証明せよ。
(1)
\[
(b - a)^2 < \int_a^b x^2 \, dx \int_a^b \frac{dx}{x^2}
\]
(2)
\[
(b - a)^2 \leq \int_a^b h(x) \, dx \int_a^b \frac{dx}{h(x)}
\]
【受験算数】1から1000までの整数について、次の問いに答えなさい。(1)12でも16でもわり切れない数は何個ありますか。(2)12でも16でもわり切れるが、18では割り切れない整数は何個ありますか。

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題
教材:
#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
1から1000までの整数について、次の問いに答えなさい。
(1)12でも16でもわり切れない数は何個ありますか。
(2)12でも16でもわり切れるが、18では割り切れない整数は何個ありますか。
この動画を見る
1から1000までの整数について、次の問いに答えなさい。
(1)12でも16でもわり切れない数は何個ありますか。
(2)12でも16でもわり切れるが、18では割り切れない整数は何個ありますか。
【中学理科】【水素の発生②】グラフは、30㎤の塩酸にいろいろな量のアルミニウムをとかし、気体が発生したあとに水分を蒸発させ、残った固体の重さをはかった結果です。問1この実験で使った塩酸 30㎤と過不…

単元:
#理科(中学受験)#化学分野
教材:
#マスターテキスト#マスターテキスト理科演習編standard#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
グラフは、30㎤の塩酸にいろいろな量のアルミニウムをとかし、気体が発生したあとに水分を蒸発させ、残った固体の重さをはかった結果です。
問1
この実験で使った塩酸 30㎤と過不足なく反応するアルミニウムは何gですか。
問2
アルミニウムを0.2g、0.4g入れたとき、残った固体中の塩化アルミニウムの重さをそれぞれ答えなさい。
問3
同じこさの塩酸 120㎤とアルミニウム0.4gを反応させると固体は何g残りますか。
問4
同じこさの塩酸 120㎤とアルミニウム0.4gを反応させたあと、どちらも残らないように反応させるには、塩酸とアルミニウムのどちらをどれだけ加える必要がありますか。また、あまらないように加えたあとで水分を蒸発させると何gの固体が残りますか。
この動画を見る
グラフは、30㎤の塩酸にいろいろな量のアルミニウムをとかし、気体が発生したあとに水分を蒸発させ、残った固体の重さをはかった結果です。
問1
この実験で使った塩酸 30㎤と過不足なく反応するアルミニウムは何gですか。
問2
アルミニウムを0.2g、0.4g入れたとき、残った固体中の塩化アルミニウムの重さをそれぞれ答えなさい。
問3
同じこさの塩酸 120㎤とアルミニウム0.4gを反応させると固体は何g残りますか。
問4
同じこさの塩酸 120㎤とアルミニウム0.4gを反応させたあと、どちらも残らないように反応させるには、塩酸とアルミニウムのどちらをどれだけ加える必要がありますか。また、あまらないように加えたあとで水分を蒸発させると何gの固体が残りますか。
【高校物理】放射性崩壊と質量:放射性崩壊と質量数の変化⃝トリウム232_90Thは、α崩壊、β崩壊を繰り返し、原子番号82の鉛Pbとなる。次の各問に答えよ。(1) トリウム232_90 Th の陽子…

単元:
#物理#理科(高校生)#原子
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
トリウム232_90Thは、α崩壊、β崩壊を繰り返し、原子番号82の鉛Pbとなる。次の各問に答えよ。(1) トリウム232_90 Th の陽子の数、および中性子の数はいくらか。(2) トリウム232 90 Th が放射性崩壊を繰り返してできる鉛Pbの質量数はいくらか。次の( )の中から選べ。(205 206 207 208)
この動画を見る
トリウム232_90Thは、α崩壊、β崩壊を繰り返し、原子番号82の鉛Pbとなる。次の各問に答えよ。(1) トリウム232_90 Th の陽子の数、および中性子の数はいくらか。(2) トリウム232 90 Th が放射性崩壊を繰り返してできる鉛Pbの質量数はいくらか。次の( )の中から選べ。(205 206 207 208)
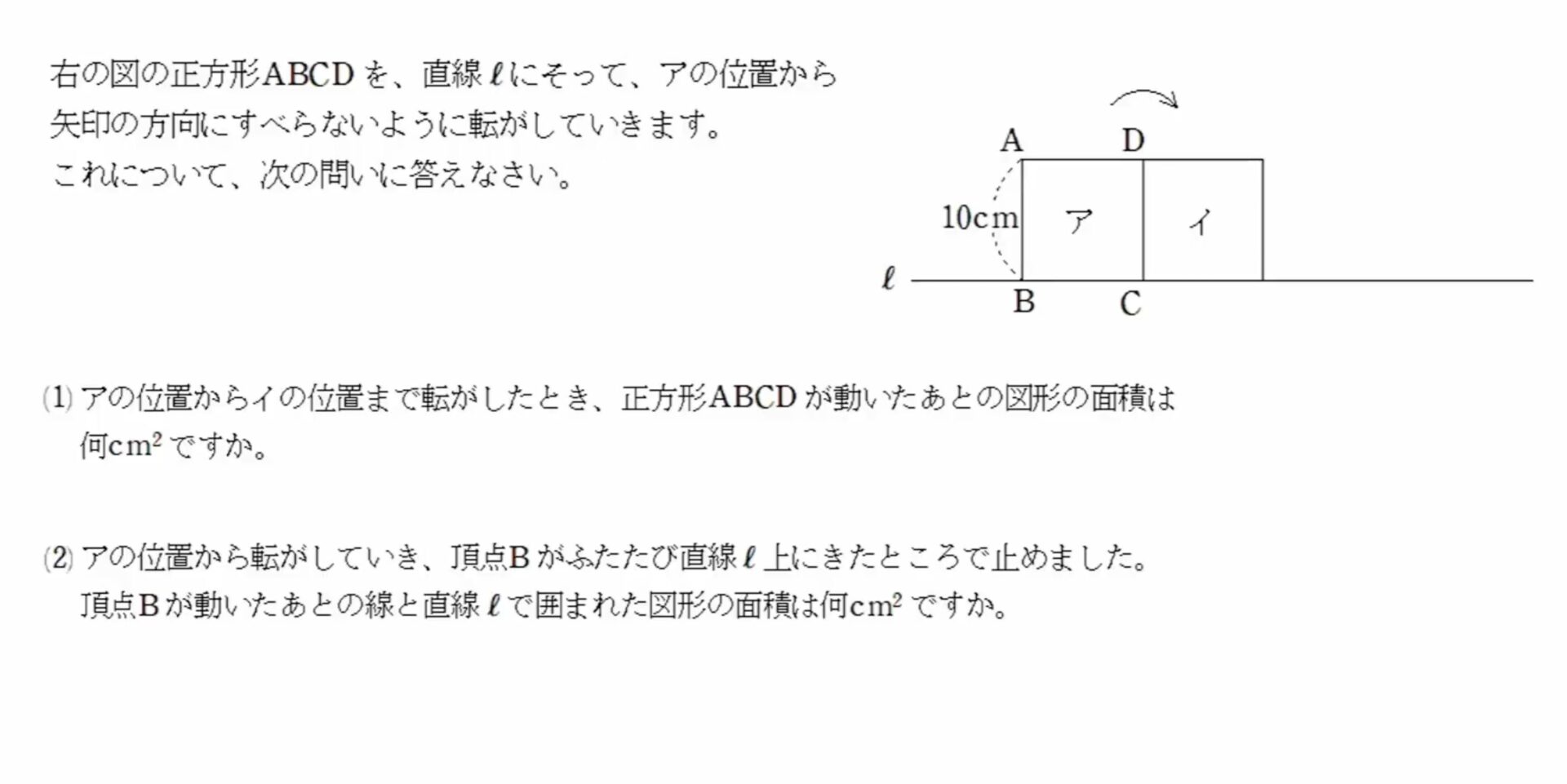
【受験算数】正方形ABCDを、直線ℓにそって、アの位置から矢印の方向にすべらないように転がしていきます。アの位置からイの位置まで転がしたとき、正方形ABCD が動いたあとの図形の面積は何cm²ですか。
単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ算数・小5下#中学受験教材#図形の移動
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図の正方形ABCDを、直線ℓにそって、アの位置から矢印の方向にすべらないように転がしていきます。
これについて、次の問いに答えなさい。
(1) アの位置からイの位置まで転がしたとき、正方形ABCD が動いたあとの図形の面積は何cm²ですか。
(2) アの位置から転がしていき、頂点Bがふたたび直線上にきたところで止めました。 頂点Bが動いたあとの線と直線で囲まれた図形の面積は何cmですか。
この動画を見る
右の図の正方形ABCDを、直線ℓにそって、アの位置から矢印の方向にすべらないように転がしていきます。
これについて、次の問いに答えなさい。
(1) アの位置からイの位置まで転がしたとき、正方形ABCD が動いたあとの図形の面積は何cm²ですか。
(2) アの位置から転がしていき、頂点Bがふたたび直線上にきたところで止めました。 頂点Bが動いたあとの線と直線で囲まれた図形の面積は何cmですか。
【英語】私立一貫校向け英語教材Lesson3-4 Stage3の英文解説

単元:
#英語(中学生)#英語(高校生)#英文法#中3英語#不定詞#不定詞(疑問詞+to,It~for to,ask(tell,want)O to,too~to,enough~to,not to)
教材:
#NT ENGLISH SERIES#中高教材#Third Edition Stage3#Lesson3
指導講師:
理数個別チャンネル
問題文全文(内容文):
The actor seems to be popular all over the world.
→ It seems that the actor is popular all over the world.
Mike seems to be concentrating on his report.
He seems to be respected by his classmates because of his knowledge of animals.
I seem to have dropped my smartphone somewhere.
The train appeared to have left when Nancy arrived at the station.
この動画を見る
The actor seems to be popular all over the world.
→ It seems that the actor is popular all over the world.
Mike seems to be concentrating on his report.
He seems to be respected by his classmates because of his knowledge of animals.
I seem to have dropped my smartphone somewhere.
The train appeared to have left when Nancy arrived at the station.
【英語】私立一貫校向け英語教材Lesson3-3 Stage3の英文解説

単元:
#英語(中学生)#英語(高校生)#英文法#中3英語#不定詞#不定詞(疑問詞+to,It~for to,ask(tell,want)O to,too~to,enough~to,not to)
教材:
#NT ENGLISH SERIES#中高教材#Third Edition Stage3#Lesson3
指導講師:
理数個別チャンネル
問題文全文(内容文):
My father made me drink a lot of water before I went jogging.
I watched my mother take pictures of the flowers.
I heard the wind blow through the trees and bushes.
I felt my heart beating wildly.
I heard my name called by one of my friends.
この動画を見る
My father made me drink a lot of water before I went jogging.
I watched my mother take pictures of the flowers.
I heard the wind blow through the trees and bushes.
I felt my heart beating wildly.
I heard my name called by one of my friends.
【数Ⅲ】【積分とその応用】次の極限値を求めよ。(1)lim[n→∞]{√(n+1)+√(n+2)+……+√(2n)}/{1+√2+√3+……+√n}他1問

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の極限値を求めよ。
(1) $\displaystyle \lim_{ n \to 0 }\dfrac{\sqrt{n+1}+\sqrt{n+2}+\sqrt{n+3}+…+\sqrt{2n}}{1+\sqrt{2}+\sqrt{3}+\sqrt{4}+…+\sqrt{n}}$
(2) $\displaystyle \lim_{ n \to 0 }\log{\sqrt[ n ]{ n+1 }}+\log{\sqrt[ n ]{ n+2 }}+\log{\sqrt[ n ]{ n+3 }}+…+\log{\sqrt[ n ]{ 2n }}-\log n$
この動画を見る
次の極限値を求めよ。
(1) $\displaystyle \lim_{ n \to 0 }\dfrac{\sqrt{n+1}+\sqrt{n+2}+\sqrt{n+3}+…+\sqrt{2n}}{1+\sqrt{2}+\sqrt{3}+\sqrt{4}+…+\sqrt{n}}$
(2) $\displaystyle \lim_{ n \to 0 }\log{\sqrt[ n ]{ n+1 }}+\log{\sqrt[ n ]{ n+2 }}+\log{\sqrt[ n ]{ n+3 }}+…+\log{\sqrt[ n ]{ 2n }}-\log n$
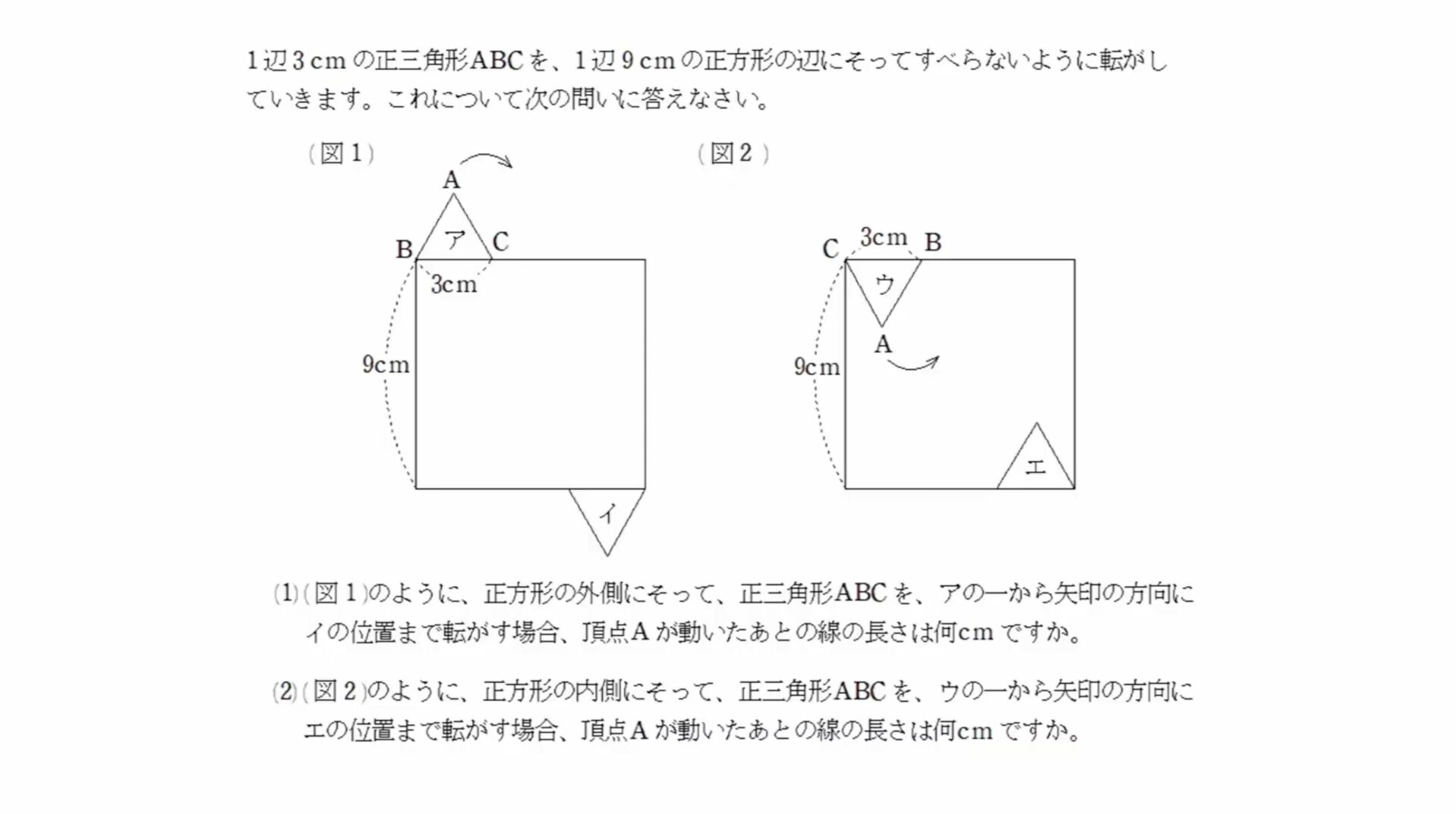
【受験算数】1辺3cmの正三角形ABCを、1辺9cmの正方形の辺の外側にそって、正三角形ABCを、アの一から矢印の方向にイの位置まで転がす場合、頂点Aが動いたあとの線の長さは何cmですか。
単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ算数・小5上#中学受験教材#平面図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
1辺3cmの正三角形ABCを、1辺9cmの正方形の辺にそってすべらないように転がしていきます。これについて次の問いに答えなさい。
(1)(図1)のように、正方形の外側にそって、正三角形ABCを、アの一から矢印の方向にイの位置まで転がす場合、頂点Aが動いたあとの線の長さは何cmですか。
(2)(図2)のように、正方形の内側にそって、正三角形ABCを、ウの一から矢印の方向にエの位置まで転がす場合、頂点Aが動いたあとの線の長さは何cmですか。
この動画を見る
1辺3cmの正三角形ABCを、1辺9cmの正方形の辺にそってすべらないように転がしていきます。これについて次の問いに答えなさい。
(1)(図1)のように、正方形の外側にそって、正三角形ABCを、アの一から矢印の方向にイの位置まで転がす場合、頂点Aが動いたあとの線の長さは何cmですか。
(2)(図2)のように、正方形の内側にそって、正三角形ABCを、ウの一から矢印の方向にエの位置まで転がす場合、頂点Aが動いたあとの線の長さは何cmですか。
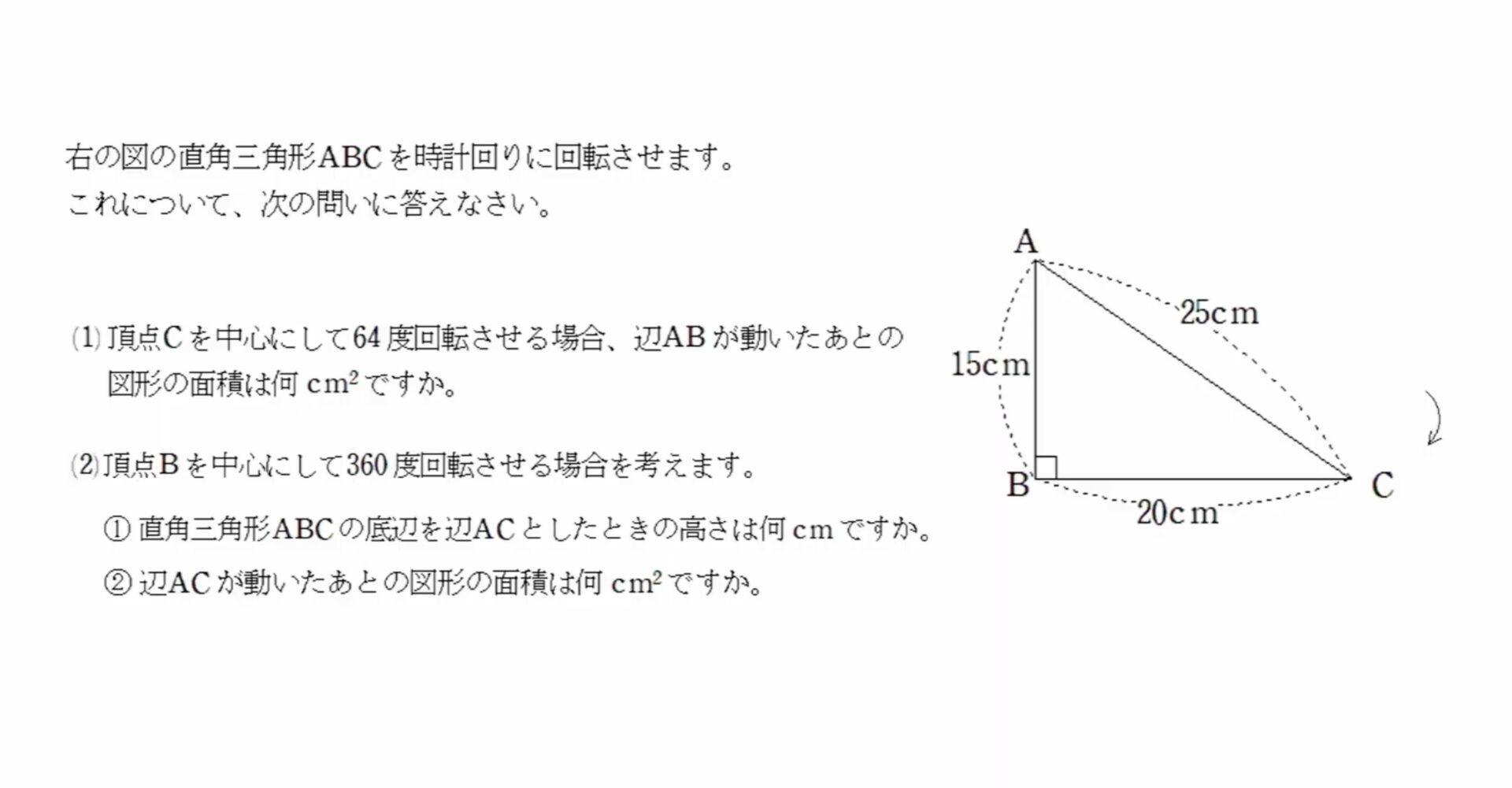
【受験算数】図の直角三角形ABCを時計回りに回転させます。頂点Cを中心にして64度回転させる場合、辺ABが動いたあとの図形の面積は何cm²ですか。
単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ#予習シ算数・小5上#中学受験教材#平面図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
図の直角三角形ABCを時計回りに回転させます。
これについて、次の問いに答えなさい。
(1) 頂点Cを中心にして64度回転させる場合、辺ABが動いたあとの図形の面積は何cm²ですか。
(2) 頂点Bを中心にして360度回転させる場合を考えます。
①直角三角形ABCの底辺を辺ACとしたときの高さは何cmですか。
② 辺ACが動いたあとの図形の面積は何cm²ですか。
この動画を見る
図の直角三角形ABCを時計回りに回転させます。
これについて、次の問いに答えなさい。
(1) 頂点Cを中心にして64度回転させる場合、辺ABが動いたあとの図形の面積は何cm²ですか。
(2) 頂点Bを中心にして360度回転させる場合を考えます。
①直角三角形ABCの底辺を辺ACとしたときの高さは何cmですか。
② 辺ACが動いたあとの図形の面積は何cm²ですか。
【数Ⅲ】【積分とその応用】次の極限値を求めよ。(1) lim[x→0]1/x∫[0→x]1/(1+cost)dt(2) lim[x→0]∫[0→x](1+sint)²/xdt他1問

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
導関数、定積分の定義を利用して、次の極限値を求めよ。
(1) $\displaystyle \lim_{ x \to 0 }\dfrac{1}{x}\int_0^x \dfrac{1}{1+cost}dt$
(2) $\displaystyle \lim_{ x \to 0 }\int_0^x \dfrac{(1+sint)^2}{x}dt$
(3) $\displaystyle \lim_{ x \to 0 }\int_0^{x^2} \dfrac{cos⁵t}{x}dt$
この動画を見る
導関数、定積分の定義を利用して、次の極限値を求めよ。
(1) $\displaystyle \lim_{ x \to 0 }\dfrac{1}{x}\int_0^x \dfrac{1}{1+cost}dt$
(2) $\displaystyle \lim_{ x \to 0 }\int_0^x \dfrac{(1+sint)^2}{x}dt$
(3) $\displaystyle \lim_{ x \to 0 }\int_0^{x^2} \dfrac{cos⁵t}{x}dt$
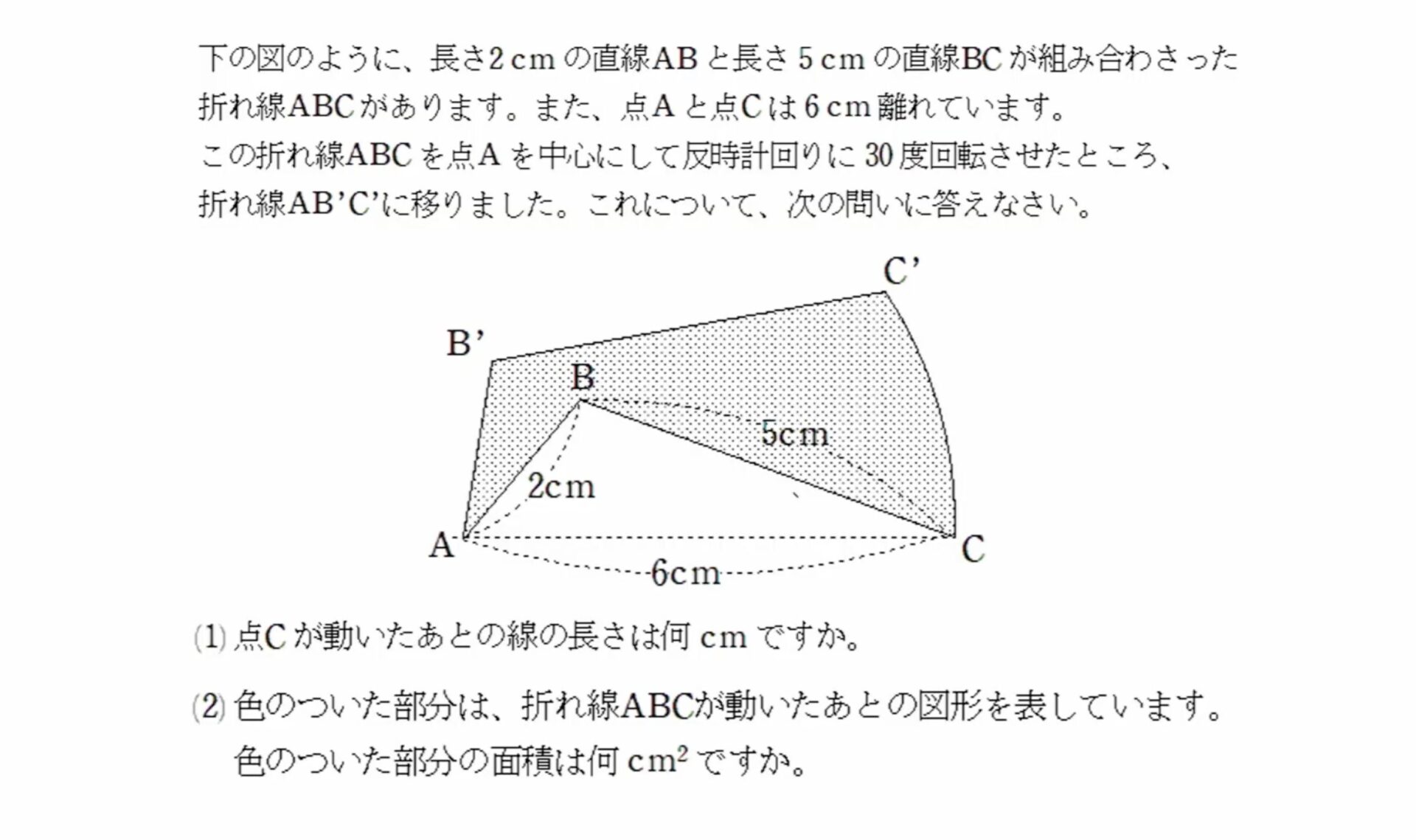
【受験算数】長さ2cmの直線ABと長さ5cmの直線BCが組み合わさった折れ線ABCがあります。また点Aと点Cは6cm離れています。この折れ線ABCを点Aを中心にして反時計回りに30度回転させたところ…
単元:
#算数(中学受験)#平面図形#図形の移動
教材:
#予習シ算数・小5上#中学受験教材#平面図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の図のように、長さ2cmの直線ABと長さ5cmの直線BCが組み合わさった折れ線ABCがあります。また、点Aと点Cは6cm離れています。
この折れ線ABCを点Aを中心にして反時計回りに30度回転させたところ、 折れ線AB'C'に移りました。これについて、次の問いに答えなさい。
(1) 点Cが動いたあとの線の長さは何cmですか。
(2) 色のついた部分は、折れ線ABCが動いたあとの図形を表しています。 色のついた部分の面積は何cm²ですか。
この動画を見る
下の図のように、長さ2cmの直線ABと長さ5cmの直線BCが組み合わさった折れ線ABCがあります。また、点Aと点Cは6cm離れています。
この折れ線ABCを点Aを中心にして反時計回りに30度回転させたところ、 折れ線AB'C'に移りました。これについて、次の問いに答えなさい。
(1) 点Cが動いたあとの線の長さは何cmですか。
(2) 色のついた部分は、折れ線ABCが動いたあとの図形を表しています。 色のついた部分の面積は何cm²ですか。
【数A】【数と式】整数xが5個存在するようなaの値の範囲を求めよ。

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
$7x-5 > 13-2x$
$x+a \geqq 3x+5$
整数$x$が5個存在するような$a$の値の範囲を求めよ。
この動画を見る
$7x-5 > 13-2x$
$x+a \geqq 3x+5$
整数$x$が5個存在するような$a$の値の範囲を求めよ。
【数A】【数と式】次のうち、小数点以下が√7 と同じになるのはどれ?

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のうち、小数点以下が$\sqrt{7}$と同じになるのはどれ?
$\sqrt{11-4\sqrt{7}} $
$\sqrt{10-\sqrt{84}} $
$\sqrt{16-3\sqrt{28}} $
この動画を見る
次のうち、小数点以下が$\sqrt{7}$と同じになるのはどれ?
$\sqrt{11-4\sqrt{7}} $
$\sqrt{10-\sqrt{84}} $
$\sqrt{16-3\sqrt{28}} $
【数A】【数と式】つぎの等式のどこが間違えっているでしょう。√(4-2√3)=√(1+3-2√1・3)=√(√1-√3)²=√1-√3=1-√3

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の二重根号を外しなさい
$\sqrt{4-2\sqrt{3}} $
※解法に間違いがあるので
見つけましょう!
この動画を見る
次の二重根号を外しなさい
$\sqrt{4-2\sqrt{3}} $
※解法に間違いがあるので
見つけましょう!
【受験算数】5つの整数のうち4つの数の平均を取り、残りの1つの数を加えることを、考えられるすべての場合について実行したところ、49,52,58,64,67という数が得られた。5つの整数を小さい順に…

単元:
#算数(中学受験)#計算と数の性質#数の性質その他
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
5つの整数があります。このうち4つの数の平均を取り、残りの1つの数を加えることを、考えられるすべての場合について実行したところ、49,52,58,64,67という数が得られました。5つの整数を小さい順に答えなさい。
この動画を見る
5つの整数があります。このうち4つの数の平均を取り、残りの1つの数を加えることを、考えられるすべての場合について実行したところ、49,52,58,64,67という数が得られました。5つの整数を小さい順に答えなさい。
【英語】私立一貫校向け英語教材Lesson3-2 Stage3の英文解説

単元:
#英語(中学生)#英語(高校生)#英文法#中3英語#不定詞#不定詞(疑問詞+to,It~for to,ask(tell,want)O to,too~to,enough~to,not to)
教材:
#NT ENGLISH SERIES#中高教材#Third Edition Stage3#Lesson3
指導講師:
理数個別チャンネル
問題文全文(内容文):
Would you give me something hot to drink?
We walked along the river and looked for a bench to sit on.
Can you lend me something to write with?
We looked for a bench to sit on.
Michael came to realize the importance of teamwork.
He got to know the members of the team very well.
George seems to like the latest novel by the writer.
この動画を見る
Would you give me something hot to drink?
We walked along the river and looked for a bench to sit on.
Can you lend me something to write with?
We looked for a bench to sit on.
Michael came to realize the importance of teamwork.
He got to know the members of the team very well.
George seems to like the latest novel by the writer.
【英語】私立一貫校向け英語教材Lesson3-1 Stage3の英文解説

単元:
#英語(中学生)#英語(高校生)#英文法#中3英語#不定詞#不定詞(疑問詞+to,It~for to,ask(tell,want)O to,too~to,enough~to,not to)
教材:
#NT ENGLISH SERIES#中高教材#Third Edition Stage3#Lesson3
指導講師:
理数個別チャンネル
問題文全文(内容文):
You were foolish to play football on such a hot day.
It was careless of them to forget their water bottles.
It is kind of you to help me with my report.
Meg has decided not to stay up late.
She studied hard in order not to fail the math test.
Take care not to catch a cold before the test.
この動画を見る
You were foolish to play football on such a hot day.
It was careless of them to forget their water bottles.
It is kind of you to help me with my report.
Meg has decided not to stay up late.
She studied hard in order not to fail the math test.
Take care not to catch a cold before the test.
【数A】【数と式】二重根号を外した形を求めよ(1) √(4+√7)(2) √(7-√33)(3) √(10+5√3)

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
二重根号を外した形を求めよ
(1) $\sqrt{4+\sqrt{7}} $
(2) $\sqrt{7-\sqrt{33}} $
(3) $\sqrt{10+5\sqrt{3}} $
この動画を見る
二重根号を外した形を求めよ
(1) $\sqrt{4+\sqrt{7}} $
(2) $\sqrt{7-\sqrt{33}} $
(3) $\sqrt{10+5\sqrt{3}} $
【数A】【数と式】二重根号を外した形を求めよ(1) √(5+√24) (2) √(11+4√6)(3) √(12-8√2)

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
二重根号を外した形を求めよ
(1) $\sqrt{5+\sqrt{24}} $
(2) $\sqrt{11+4\sqrt{6}} $
(3) $\sqrt{12-8\sqrt{2}} $
この動画を見る
二重根号を外した形を求めよ
(1) $\sqrt{5+\sqrt{24}} $
(2) $\sqrt{11+4\sqrt{6}} $
(3) $\sqrt{12-8\sqrt{2}} $
【数A】【数と式】二重根号を外した形を求めよ(1) √(4-2√3)(2) √(17-2√42)(3) √(9-2√20)

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
二重根号を外した形を求めよ
(1) $\sqrt{4-2\sqrt{3}} $
(2) $\sqrt{17-2\sqrt{42}} $
(3) $\sqrt{9-2\sqrt{20}} $
この動画を見る
二重根号を外した形を求めよ
(1) $\sqrt{4-2\sqrt{3}} $
(2) $\sqrt{17-2\sqrt{42}} $
(3) $\sqrt{9-2\sqrt{20}} $
【受験算数】5つの整数のうち4つの数の平均を取り、残りの1つの数を加えることを、考えられるすべての場合について実行したところ、47,53,56,59,65という数が得られた。5つの整数を小さい順に…

単元:
#算数(中学受験)#計算と数の性質#数の性質その他
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
5つの整数があります。このうち4つの数の平均を取り、残りの1つの数を加えることを、考えられるすべての場合について実行したところ、47,53, 56, 59, 65 という数が得られました。5つの整数を小さい順に答えなさい。
この動画を見る
5つの整数があります。このうち4つの数の平均を取り、残りの1つの数を加えることを、考えられるすべての場合について実行したところ、47,53, 56, 59, 65 という数が得られました。5つの整数を小さい順に答えなさい。
【受験算数】45人のクラスで国語と算数のテストがあり、国語2題のうち1 番ができた人が37人、2番ができた人が26人、2題ともできなかった人が1人いた。1題50点として国語で100点をとった人は何人?

単元:
#算数(中学受験)#文章題#文章題その他
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
45人のクラスで国語と算数のテストがありました。その結果は国語2題のうち1 番がてきた人が37人、2番がてきた人が26人、2題ともできなかった人が1人いました。算数については2題のうち1番ができた人が36人、1番、2番のうち1題だけてきた人が35人いました。そして算数の平均点は50点でした。国語、算数とも1題50点として、次の問いに答えなさい。
(1) 国語で100点をとった人は何人ですか。
(2) 国語の平均点は何点ですか。
(3) 算数で100点をとった人は何人ですか。
この動画を見る
45人のクラスで国語と算数のテストがありました。その結果は国語2題のうち1 番がてきた人が37人、2番がてきた人が26人、2題ともできなかった人が1人いました。算数については2題のうち1番ができた人が36人、1番、2番のうち1題だけてきた人が35人いました。そして算数の平均点は50点でした。国語、算数とも1題50点として、次の問いに答えなさい。
(1) 国語で100点をとった人は何人ですか。
(2) 国語の平均点は何点ですか。
(3) 算数で100点をとった人は何人ですか。
【数A】【数と式】(1) a³+b³+c³-3abc を因数分解せよ(2) (1)の結果を利用して x³+y³-3xy+1 を因数分解せよ

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#数と式#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1) $a^3+b^3+c^3-3abc$ を因数分解せよ
(2) (1)の結果を利用して $x^3+y^3-3xy+1$ を因数分解せよ
この動画を見る
(1) $a^3+b^3+c^3-3abc$ を因数分解せよ
(2) (1)の結果を利用して $x^3+y^3-3xy+1$ を因数分解せよ




