 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【高校数学】毎日積分65日目~47都道府県制覇への道~【⑨高知(高知大学)】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#高知大学#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)すべての実数$x$に対して
$sin3x=3sinx-4sin^3x$
$cos3x=-3cosx+4cos^3x$
が成り立つことを、加法定理と2倍角の公式を用いて示せ。
(2)実数$θ$を、$\displaystyle\frac{π}{3}<θ<\frac{π}{2}$と$cos3θ=\displaystyle-\frac{11}{16}$を同時に満たすものとする。このとき、$cosθ$を求めよ。
(3)(2)の$θ$に対して、定積分$\displaystyle\int_0^θsin^5xdx$を求めよ。
【高知大学 2023】
この動画を見る
(1)すべての実数$x$に対して
$sin3x=3sinx-4sin^3x$
$cos3x=-3cosx+4cos^3x$
が成り立つことを、加法定理と2倍角の公式を用いて示せ。
(2)実数$θ$を、$\displaystyle\frac{π}{3}<θ<\frac{π}{2}$と$cos3θ=\displaystyle-\frac{11}{16}$を同時に満たすものとする。このとき、$cosθ$を求めよ。
(3)(2)の$θ$に対して、定積分$\displaystyle\int_0^θsin^5xdx$を求めよ。
【高知大学 2023】
【22日目】毎日3分多義語:島田先生に抜き打ちテスト③【毎朝7時投稿】#英単語 #毎日3分多義語 #shorts
単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
理数個別チャンネル
問題文全文(内容文):
<今日の単語>
firm
gift
hot
出典:島田先生の記憶
この動画を見る
<今日の単語>
firm
gift
hot
出典:島田先生の記憶
【高校数学】毎日積分64日目~47都道府県制覇への道~【⑧福岡】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$xy$平面上の曲線$C$を、媒介変数tを用いて次のように定める。
$x=t+2\sin^{2t}, y=t+\sin t (0\lt t\lt \pi)$
以下の問いに答えよ。
(1)曲線$C$に接する直線のうち$y$軸と平行なものがいくつあるか求めよ。
(2)曲線$C$のうち$y≦x$の領域にある部分と直線$y=x$で囲まれた図形の面積を求めよ。
【九州大学 2023】
この動画を見る
$xy$平面上の曲線$C$を、媒介変数tを用いて次のように定める。
$x=t+2\sin^{2t}, y=t+\sin t (0\lt t\lt \pi)$
以下の問いに答えよ。
(1)曲線$C$に接する直線のうち$y$軸と平行なものがいくつあるか求めよ。
(2)曲線$C$のうち$y≦x$の領域にある部分と直線$y=x$で囲まれた図形の面積を求めよ。
【九州大学 2023】
【21日目】毎日3分多義語:島田先生に抜き打ちテスト②【毎朝7時投稿】#英単語 #毎日3分多義語 #shorts

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
理数個別チャンネル
問題文全文(内容文):
<今日の単語>
capital
drop
fire
firm
出典:島田先生の記憶
この動画を見る
<今日の単語>
capital
drop
fire
firm
出典:島田先生の記憶
【高校数学】毎日積分63日目~47都道府県制覇への道~【⑦佐賀】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の問に答えよ。
(1)等式$(\tan\theta)’=\dfrac{1}{\cos^2\theta}$を示せ。また、定積分$\displaystyle \int_{0}^{\frac{\pi}{4}}\dfrac{1}{\cos^2\theta}d\theta$の値を求めよ。
(2)等式$\dfrac{\cos\theta}{1+\sin\theta}+\dfrac{\cosθ}{1-\sin\theta}=\dfrac{2}{\cos\theta}$を示せ。また、定積分$\displaystyle \int_{0}^{\frac{\pi}{6}}\dfrac{1}{\cos\theta}d\theta$の値を求めよ。
(3)定積分$\displaystyle \int_{0}^{\frac{\pi}{6}}\dfrac{1}{\cos^3\theta}d\theta$の値を求めよ。
【佐賀大学 2023】
この動画を見る
次の問に答えよ。
(1)等式$(\tan\theta)’=\dfrac{1}{\cos^2\theta}$を示せ。また、定積分$\displaystyle \int_{0}^{\frac{\pi}{4}}\dfrac{1}{\cos^2\theta}d\theta$の値を求めよ。
(2)等式$\dfrac{\cos\theta}{1+\sin\theta}+\dfrac{\cosθ}{1-\sin\theta}=\dfrac{2}{\cos\theta}$を示せ。また、定積分$\displaystyle \int_{0}^{\frac{\pi}{6}}\dfrac{1}{\cos\theta}d\theta$の値を求めよ。
(3)定積分$\displaystyle \int_{0}^{\frac{\pi}{6}}\dfrac{1}{\cos^3\theta}d\theta$の値を求めよ。
【佐賀大学 2023】
【20日目】毎日3分多義語:島田先生に抜き打ちテスト①【毎朝7時投稿】#英単語 #毎日3分多義語 #shorts

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
理数個別チャンネル
問題文全文(内容文):
<今日の単語>
book
bow
bat
case
capital
出典:島田先生の記憶
この動画を見る
<今日の単語>
book
bow
bat
case
capital
出典:島田先生の記憶
故郷長崎の積分でまさかの大苦戦…!? #shorts #高校数学 #毎日積分
【高校数学】無理関数のグラフの裏ワザ!例題もあるよ!

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の無理関数のグラフをかけ。
(1)$y=\sqrt{x+2}$
(2)$y=\sqrt{-3x-6}$
(3)$y=-\sqrt{7-4x}$
(4)$y=-\sqrt{\dfrac{1}{2}x-3}$
この動画を見る
次の無理関数のグラフをかけ。
(1)$y=\sqrt{x+2}$
(2)$y=\sqrt{-3x-6}$
(3)$y=-\sqrt{7-4x}$
(4)$y=-\sqrt{\dfrac{1}{2}x-3}$
【高校数学】無理関数のグラフの裏ワザ!例題もあるよ!

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の無理関数のグラフをかけ。
(1)$ y=\sqrt{x+2}$
(2)$ y=\sqrt{ー3x-6}$
(3)$ y=-\sqrt{7-4x}$
(4)$ y=-\sqrt{\frac{1}{2}x-3}$
この動画を見る
次の無理関数のグラフをかけ。
(1)$ y=\sqrt{x+2}$
(2)$ y=\sqrt{ー3x-6}$
(3)$ y=-\sqrt{7-4x}$
(4)$ y=-\sqrt{\frac{1}{2}x-3}$
【高校数学】毎日積分62日目~47都道府県制覇への道~【⑥長崎】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#長崎大学#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$ a,b$を定数とする。すべての実数$x$で連続な関数$f(x)$について、等式
$\displaystyle\int_a^bf(x)dx = \displaystyle\int_a^bf(a+b-x)dx$
が成り立つことを証明せよ。また、定積分$\displaystyle\int_1^2\frac{x^2}{x^2+(3-x)^2}dx$を求めよ。
【長崎大学 2023】
この動画を見る
$ a,b$を定数とする。すべての実数$x$で連続な関数$f(x)$について、等式
$\displaystyle\int_a^bf(x)dx = \displaystyle\int_a^bf(a+b-x)dx$
が成り立つことを証明せよ。また、定積分$\displaystyle\int_1^2\frac{x^2}{x^2+(3-x)^2}dx$を求めよ。
【長崎大学 2023】
高校数学:数学検定準1級2次:問題6 3次方程式の解と係数の関係

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#数学検定#数学検定準1級#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の2つの3次方程式
$x^3+10x^2+ax+14=0$
$x^3+2x^2+bx-2=0$
はそれぞれ異なる3個の解をもちますが、そのうちの2個は共通な解です。このと き、定数$a,b$の値および共通な2個の解を求めなさい。
この動画を見る
次の2つの3次方程式
$x^3+10x^2+ax+14=0$
$x^3+2x^2+bx-2=0$
はそれぞれ異なる3個の解をもちますが、そのうちの2個は共通な解です。このと き、定数$a,b$の値および共通な2個の解を求めなさい。
毎日積分~47都道府県制覇への道~ #Shorts #高校数学 #積分
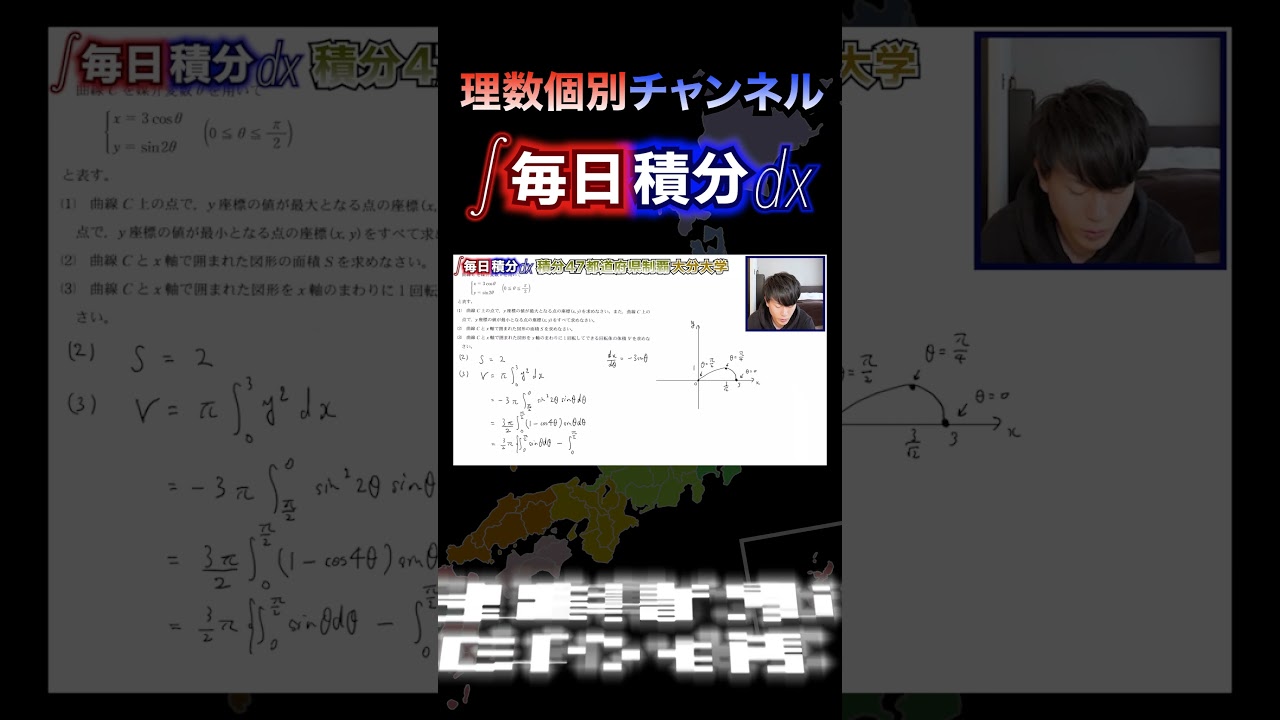
【高校数学】毎日積分61日目~47都道府県制覇への道~【⑤大分】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#大分大学#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
曲線$C$を媒介変数$θ$を用いて
$\begin{equation}
\left\{ \,
\begin{aligned}
x=3cosθ \\
y=sin2θ
\end{aligned}
\right.
\end{equation}$
$(0≦θ≦π/2)$
と表す。
(1)曲線$C$上の点で、$y$座標の値が最大となる点の座標$(x,y)$を求めなさい。また、曲線$C$上の点で、$y$座標の値が最小となる点の座標$(x,y)$をすべて求めなさい。
(2)曲線$C$と$x$軸で囲まれた図形の面積$S$を求めなさい。
(3)曲線$C$と$x$軸で囲まれた図形を$x$軸のまわりに1回転してできる回転体の体積$V$を求めなさい。
【大分大学 2023】
この動画を見る
曲線$C$を媒介変数$θ$を用いて
$\begin{equation}
\left\{ \,
\begin{aligned}
x=3cosθ \\
y=sin2θ
\end{aligned}
\right.
\end{equation}$
$(0≦θ≦π/2)$
と表す。
(1)曲線$C$上の点で、$y$座標の値が最大となる点の座標$(x,y)$を求めなさい。また、曲線$C$上の点で、$y$座標の値が最小となる点の座標$(x,y)$をすべて求めなさい。
(2)曲線$C$と$x$軸で囲まれた図形の面積$S$を求めなさい。
(3)曲線$C$と$x$軸で囲まれた図形を$x$軸のまわりに1回転してできる回転体の体積$V$を求めなさい。
【大分大学 2023】
【前編】2023年度K塾共通テスト高2模試「情報Ⅰ」(2024年1月28日(日)実施) の講評 ※後編は共通テスト「情報Ⅰ」専門チャンネルで公開

単元:
#情報Ⅰ(高校生)#模試解説・過去問解説#【河合塾】全統共通テスト模試
指導講師:
理数個別チャンネル
問題文全文(内容文):
2023年度K塾共通テスト高2模試「情報Ⅰ」(2024年1月28日(日)実施) の講評をしていきます.
この動画を見る
2023年度K塾共通テスト高2模試「情報Ⅰ」(2024年1月28日(日)実施) の講評をしていきます.
【前編】2024年1月実施の高2K塾模試【情報Ⅰ】の講評 ※後編は共通テスト「情報Ⅰ」専門チャンネルで公開

単元:
#情報Ⅰ(高校生)#模試解説・過去問解説
指導講師:
理数個別チャンネル
問題文全文(内容文):
2024年1月実施の高2全統模試【情報Ⅰ】の講評とそこから分かる勉強法について座談会しました。
■出演者
・ユースケ(情報初心者・司会)
・うっち~(元エンジニア)
・ぐっさん(基本情報技術者)
・NI・SHI・NO(情報初心者)
この動画を見る
2024年1月実施の高2全統模試【情報Ⅰ】の講評とそこから分かる勉強法について座談会しました。
■出演者
・ユースケ(情報初心者・司会)
・うっち~(元エンジニア)
・ぐっさん(基本情報技術者)
・NI・SHI・NO(情報初心者)
高校数学:数学検定準1級1次:問題6,7 双曲線の焦点、関数の極限

単元:
#数学検定・数学甲子園・数学オリンピック等#平面上の曲線#関数と極限#2次曲線#関数の極限#数学検定#数学検定準1級#数学(高校生)#数C#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
xy平面上の双曲線
$\frac{x^2}{36}-\frac{y^2}{64}=-1$
の焦点の座標を求めなさい。
次の極限値を求めなさい。
$\displaystyle \lim_{ x \to 1 }\displaystyle \frac{x^2+2x-3}{\sqrt[ 3 ]{ x }-1}$
この動画を見る
xy平面上の双曲線
$\frac{x^2}{36}-\frac{y^2}{64}=-1$
の焦点の座標を求めなさい。
次の極限値を求めなさい。
$\displaystyle \lim_{ x \to 1 }\displaystyle \frac{x^2+2x-3}{\sqrt[ 3 ]{ x }-1}$
【高校数学】毎日積分60日目~47都道府県制覇への道~【④熊本】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#熊本大学#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
定積分$\displaystyle \int_1^{\sqrt{t}}4tx(1-tx^2)e^{-tx^2}logxdx$の値を$t$を用いて表せ。
【熊本大学 2023】
この動画を見る
定積分$\displaystyle \int_1^{\sqrt{t}}4tx(1-tx^2)e^{-tx^2}logxdx$の値を$t$を用いて表せ。
【熊本大学 2023】
【数学】中高一貫校問題集 数学3 数式・関数編 111 実数解が存在することの証明

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材:
#TK数学#TK数学問題集3(数式・関数編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
a,b,cは実数の定数で、a≠0とする。2次方程式ax²+bx+c=0が、次の各場合に必ず実数解をもつことを証明せよ。
(1)$b=\frac{a}{2}+2c$
(2)$a+c=0$
(3)aとcが異符号
この動画を見る
a,b,cは実数の定数で、a≠0とする。2次方程式ax²+bx+c=0が、次の各場合に必ず実数解をもつことを証明せよ。
(1)$b=\frac{a}{2}+2c$
(2)$a+c=0$
(3)aとcが異符号
【高校数学】毎日積分59日目~47都道府県制覇への道~【③宮崎】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数$\displaystyle f(x)=\frac{x}{1+x^2}$および座標平面上の原点$O$を通る曲線$C:y=f(x)$について、次の各問に答えよ。
(1)$f(x)$の導関数$f'(x)$および第2次導関数$f''(x)$を求めよ。
(2)直線$y=ax$が曲線$C$に$O$で接するときの定数$a$の値を求めよ。また、このとき、$x >0$において、$ax>f(x)$が成り立つことを示せ。
(3)関数$f(x)$の増減、極値、曲線$C$の凹凸、変曲点および漸近線を調べて、曲線$C$の概形をかけ。
(4)(2)で求めた$a$の値に対し、曲線$C$と直線$y=ax$および直線$x=\sqrt{3}$で囲まれた部分の面積$S$を求めよ。
【宮崎大学 2023】
この動画を見る
関数$\displaystyle f(x)=\frac{x}{1+x^2}$および座標平面上の原点$O$を通る曲線$C:y=f(x)$について、次の各問に答えよ。
(1)$f(x)$の導関数$f'(x)$および第2次導関数$f''(x)$を求めよ。
(2)直線$y=ax$が曲線$C$に$O$で接するときの定数$a$の値を求めよ。また、このとき、$x >0$において、$ax>f(x)$が成り立つことを示せ。
(3)関数$f(x)$の増減、極値、曲線$C$の凹凸、変曲点および漸近線を調べて、曲線$C$の概形をかけ。
(4)(2)で求めた$a$の値に対し、曲線$C$と直線$y=ax$および直線$x=\sqrt{3}$で囲まれた部分の面積$S$を求めよ。
【宮崎大学 2023】
【高校数学】分数関数と一次関数の不等式をグラフを使わない裏ワザ!②

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の不等式を解け。
$\dfrac{2x}{x+1}\geqq x+6$
この動画を見る
次の不等式を解け。
$\dfrac{2x}{x+1}\geqq x+6$
【高校数学】分数関数と一次関数の不等式をグラフを使わない裏ワザ!②

単元:
#関数と極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の不等式を解け。
$\displaystyle\frac{2x}{x+1}≧x+6$
この動画を見る
次の不等式を解け。
$\displaystyle\frac{2x}{x+1}≧x+6$
【高校数学】毎日積分58日目~47都道府県制覇への道~【②鹿児島】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#鹿児島大学#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$x>0$で定義された曲線
$C : y=(log x)^2$
を考える
(1)$a$を正の実数とする時、点$P(a,(log a)^2)$における曲線$C$の接線$L$の方程式を求めよ。
(2)$a>1$のとき、接線$L$と$x$軸の交点の$x$座標が最大となる場合の$a$の値$a_0$を求めよ。
(3)$a$の値が(2)の$a_0$に等しいとき、直線$L$の$y≧0$の部分と曲線$C$と$x$軸で囲まれた部分を、$x$軸の周りに1回転させてできる図形の体積を求めよ。
【鹿児島大学 2023】
この動画を見る
$x>0$で定義された曲線
$C : y=(log x)^2$
を考える
(1)$a$を正の実数とする時、点$P(a,(log a)^2)$における曲線$C$の接線$L$の方程式を求めよ。
(2)$a>1$のとき、接線$L$と$x$軸の交点の$x$座標が最大となる場合の$a$の値$a_0$を求めよ。
(3)$a$の値が(2)の$a_0$に等しいとき、直線$L$の$y≧0$の部分と曲線$C$と$x$軸で囲まれた部分を、$x$軸の周りに1回転させてできる図形の体積を求めよ。
【鹿児島大学 2023】
【19日目】毎日3分多義語 ~今日から1日5個覚えましょう!~ 【毎朝7時投稿】

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
教材:
#中高教材#英単語最前線2500(研究社)
指導講師:
理数個別チャンネル
問題文全文(内容文):
<今日の単語>
available
pain
public
express
tongue
出典:英単語最前線2500(研究社)
この動画を見る
<今日の単語>
available
pain
public
express
tongue
出典:英単語最前線2500(研究社)
高校数学:数Ⅰ:図形と計量:三角比への応用:「三角形の形状」の考え方!

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$△ABC$において,$\sin A=\cos B\sin C$が成り立つとき,この三角形はどのような形をしているか。
$△ABC$において,次の等式が成り立つとき,この三角形はどのような形をしているか。
(1) $a\sin A=b\sin B$
(2) $\sin A=2\cos B\sin C$
(3) $a\cos A=b\cos B$
この動画を見る
$△ABC$において,$\sin A=\cos B\sin C$が成り立つとき,この三角形はどのような形をしているか。
$△ABC$において,次の等式が成り立つとき,この三角形はどのような形をしているか。
(1) $a\sin A=b\sin B$
(2) $\sin A=2\cos B\sin C$
(3) $a\cos A=b\cos B$
【数学】中高一貫校問題集 数学3 数式・関数編 109 虚数を含む2次方程式の解法
単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
教材:
#TK数学#TK数学問題集3(数式・関数編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の等式を満たす実数xの値を求めよ。
(1)(2+i)x²-(1+6i)x-2(3-4i)=0
(2)(3+2i)x²+(8+5i)x-3(1+i)=0
この動画を見る
次の等式を満たす実数xの値を求めよ。
(1)(2+i)x²-(1+6i)x-2(3-4i)=0
(2)(3+2i)x²+(8+5i)x-3(1+i)=0
毎日積分~積分47都道府県制覇への道~ #Shorts #毎日積分 #高校数学
【高校数学】毎日積分57日目~47都道府県制覇への道~【①沖縄】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$a$を実数とし、$f(x)=xe^{-|x|}, g(x)=ax$とおく。次の問いに答えよ。
問1 $f(x)$の増減を調べ、$y=f(x)$のグラフの概形をかけ。ただし$\displaystyle \lim_{x\to \infty}xe^{-x}=0$は証明なしに用いてよい。
問2 $0<a<1$のとき、曲線$y=f(x)$と直線$y=g(x)$で囲まれた2つの部分の面積の和を求めよ。
【琉球大学 2023】
この動画を見る
$a$を実数とし、$f(x)=xe^{-|x|}, g(x)=ax$とおく。次の問いに答えよ。
問1 $f(x)$の増減を調べ、$y=f(x)$のグラフの概形をかけ。ただし$\displaystyle \lim_{x\to \infty}xe^{-x}=0$は証明なしに用いてよい。
問2 $0<a<1$のとき、曲線$y=f(x)$と直線$y=g(x)$で囲まれた2つの部分の面積の和を求めよ。
【琉球大学 2023】
【18日目】毎日3分多義語(Daily 3-Minute Multimeanings) ~入試に出るのは「じゃない方」の意味~【毎朝7時投稿】

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
教材:
#中高教材#ビーコン英和辞典第3版【小型版】(三省堂)#英単語最前線2500(研究社)
指導講師:
理数個別チャンネル
問題文全文(内容文):
今日は大学入試で超重要な多義語、succeedです。
出典:ビーコン英和辞典第3版【小型版】(三省堂)・英単語最前線2500(研究社)
この動画を見る
今日は大学入試で超重要な多義語、succeedです。
出典:ビーコン英和辞典第3版【小型版】(三省堂)・英単語最前線2500(研究社)
【高校数学】毎日積分56日目【難易度:★】【毎日17時投稿】

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\displaystyle \int_0^1\frac{1}{e^x+2e^{-x}+3}dx$
これを解け.
この動画を見る
$\displaystyle \int_0^1\frac{1}{e^x+2e^{-x}+3}dx$
これを解け.
英検1次試験合格発表後のコメントを読ませていただきました+英検2級ライティング満点生徒の再現答案を大公開!

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級
指導講師:
理数個別チャンネル
問題文全文(内容文):
英検1次試験合格発表後のコメントを読ませていただきました。
コメントくれた方々ありがとうございました!
英検2級ライティング満点生徒の再現答案も大公開しています。参考にしてください。
この動画を見る
英検1次試験合格発表後のコメントを読ませていただきました。
コメントくれた方々ありがとうございました!
英検2級ライティング満点生徒の再現答案も大公開しています。参考にしてください。




