 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
Lesson2-1 ニュートレジャー Stage2 3rd Edition【まどか's Englishがていねいに解説】

単元:
#英語(中学生)#中2英語#接続詞(and,or,but,so・when,if,because,before,after・接続詞that)
指導講師:
理数個別チャンネル
問題文全文(内容文):
従属接続詞if,because,thoughを解説しています!
この動画を見る
従属接続詞if,because,thoughを解説しています!
【英検準1級・2級ライティング】③introduction/conclusionのテンプレ紹介

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級#英検準1級
指導講師:
理数個別チャンネル
問題文全文(内容文):
「英検準1級・2級のライティング」を基礎から9割得点まで引き上げる全6編の完全版です。
英検合格にお役立てできれば嬉しいです。
この動画を見る
「英検準1級・2級のライティング」を基礎から9割得点まで引き上げる全6編の完全版です。
英検合格にお役立てできれば嬉しいです。
【英検準1級・2級ライティング】②減点されてしまう可能性がある行為

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級#英検準1級
指導講師:
理数個別チャンネル
問題文全文(内容文):
「英検準1級・2級のライティング」を基礎から9割得点まで引き上げる全6編の完全版です。
英検合格にお役立てできれば嬉しいです。
この動画を見る
「英検準1級・2級のライティング」を基礎から9割得点まで引き上げる全6編の完全版です。
英検合格にお役立てできれば嬉しいです。
【英検準1級・2級ライティング】⓪①準1級・2級それぞれの「構成点」をもぎ取る方法

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級#英検準1級
指導講師:
理数個別チャンネル
問題文全文(内容文):
「英検準1級・2級のライティング」を基礎から9割得点まで引き上げる全6編の完全版です。
英検合格にお役立てできれば嬉しいです。
この動画を見る
「英検準1級・2級のライティング」を基礎から9割得点まで引き上げる全6編の完全版です。
英検合格にお役立てできれば嬉しいです。
【数検準2級】高校数学:数学検定準2級2次:問4

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問4. a,bを定数とします。放物線$y=-x^2+4ax+b$ について、次の問いに答えなさい。
(5) 頂点の座標をa,bを用いて表しなさい。この問題は答えだけを書いてください。
(6) 放物線 $y=-x^2$ をx軸方向に1、y軸方向に5だけ平行移動したところ、上の放物線になりました。このとき、a,bの値をそれぞれ求めなさい。
この動画を見る
問4. a,bを定数とします。放物線$y=-x^2+4ax+b$ について、次の問いに答えなさい。
(5) 頂点の座標をa,bを用いて表しなさい。この問題は答えだけを書いてください。
(6) 放物線 $y=-x^2$ をx軸方向に1、y軸方向に5だけ平行移動したところ、上の放物線になりました。このとき、a,bの値をそれぞれ求めなさい。
【数検準2級】高校数学:数学検定準2級2次:問3

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学検定#数学検定準2級#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問3.次の問いに答えなさい。
(4) 右の図の四角形ABCDは平行四辺形です。また、点E、F、Gは辺ABを4等分する点で、点H、I、Jは辺CDを4等分する点です。
斜線部分の面積が10㎝²であるとき、四角形ABCDの面積を求めなさい。この問題は答えだけを書いてください。
この動画を見る
問3.次の問いに答えなさい。
(4) 右の図の四角形ABCDは平行四辺形です。また、点E、F、Gは辺ABを4等分する点で、点H、I、Jは辺CDを4等分する点です。
斜線部分の面積が10㎝²であるとき、四角形ABCDの面積を求めなさい。この問題は答えだけを書いてください。
【化学】モル比が分かれば化学の計算なんて怖くない!?4分で練習問題も含めて解説

単元:
#化学基礎2ー物質の変化#化学変化と化学反応式#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
メタン8.0gを完全燃焼するために必要な酸素の体積を求めよ。
化学反応式からモル比を求めてすべて単位変換で解説をしています。余計な公式は一切なし!化学の計算は単位変換のみで解決!
この動画を見る
メタン8.0gを完全燃焼するために必要な酸素の体積を求めよ。
化学反応式からモル比を求めてすべて単位変換で解説をしています。余計な公式は一切なし!化学の計算は単位変換のみで解決!
【化学】受験生が苦手な計算を定義から6分で解説。質量パーセント濃度からモル濃度の変換も公式を使わずに解説

単元:
#化学#化学基礎2ー物質の変化#物質量と濃度#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
質量パーセント濃度からモル濃度への変換を単位変換のみで解説をしています。
密度1.40g/㎤、質量パーセント濃度50%の硫酸がある。この硫酸のモル濃度を求めよ。
この動画を見る
質量パーセント濃度からモル濃度への変換を単位変換のみで解説をしています。
密度1.40g/㎤、質量パーセント濃度50%の硫酸がある。この硫酸のモル濃度を求めよ。
【化学】物質量の計算をマスターせよ!練習問題も含めて9分で解説!

単元:
#化学#化学基礎2ー物質の変化#物質量と濃度#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
メタン8.0グラムの時の体積を求めよ。
化学が苦手になる分岐点をすべて単位変換で解説。無駄な公式は一切使わずに小学生の知識だけで物質量の計算をマスターしよう!
この動画を見る
メタン8.0グラムの時の体積を求めよ。
化学が苦手になる分岐点をすべて単位変換で解説。無駄な公式は一切使わずに小学生の知識だけで物質量の計算をマスターしよう!
データの分析 データが変更されたときの平均、分散の関係【ユースケ・マセマティックがていねいに解説】

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のデータは、ある6人について、懸垂が何回できたかを記録したものである。
14 11 10 18 16 9(単位は回)
(1) このデータの平均値を求めよ。
(2) このデータには記録ミスがあり、18回は正しくは17回、9回は正しくは10回であった。この誤りを修正した時、このデータの平均値、分散は、修正前から増加するか、減少するか、変化しないかを答えよ。
(3)(2)の修正後、他の1人の生徒について同じように懸垂の記録を取ったところ、13回であった。この生徒を加えた7人のデータの分散は、加える前と比較して増加するか、減少するか、変化しないかを答えよ。
この動画を見る
次のデータは、ある6人について、懸垂が何回できたかを記録したものである。
14 11 10 18 16 9(単位は回)
(1) このデータの平均値を求めよ。
(2) このデータには記録ミスがあり、18回は正しくは17回、9回は正しくは10回であった。この誤りを修正した時、このデータの平均値、分散は、修正前から増加するか、減少するか、変化しないかを答えよ。
(3)(2)の修正後、他の1人の生徒について同じように懸垂の記録を取ったところ、13回であった。この生徒を加えた7人のデータの分散は、加える前と比較して増加するか、減少するか、変化しないかを答えよ。
データの分析 平均と分散だけ与えられたデータ【ユースケ・マセマティックがていねいに解説】

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
20個の値からなるデータがあり、そのうちの8個の値の平均値は3,分散は4、残りの12個の値の平均値は8、分散は9である。
(1)このデータの平均値を求めよ。
(2)このデータの分散を求めよ。
この動画を見る
20個の値からなるデータがあり、そのうちの8個の値の平均値は3,分散は4、残りの12個の値の平均値は8、分散は9である。
(1)このデータの平均値を求めよ。
(2)このデータの分散を求めよ。
数と式 真偽の調べ方【いつものシミズ君がていねいに解説】

単元:
#数Ⅰ#数と式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
a,bは実数とする。次の命題の真偽を求めよ。
(1)$ab=0$ならば$a^2+b^2=0$である。
(2)$a^2=4$ならば$\vert a+1\vert \geqq 1$である。
(3)$ab$が有理数であるならば、a、bはともに有理数である。
(4)$a+b、ab$がともに有理数ならば、a、bはともに有理数である。
全体集合を$U$とし、条件$p、q$を満たす全体の集合を、それぞれ$P.Q$とする。
命題$p$(補集合)⇒$q$が真であるとき、$P、Q$について常に成り立つ事をすべて選べ。
①$P=Q$
②$Q⊂P$
③$Q$(補集合)$⊂P$
④$P⊂Q$(補集合)
⑤$P∪Q$(補集合)$=P$
⑥$P∪Q$(補集合)$=Q$(補集合)
⑦$P∩Q=∅$
⑧$P∪Q=U$
この動画を見る
a,bは実数とする。次の命題の真偽を求めよ。
(1)$ab=0$ならば$a^2+b^2=0$である。
(2)$a^2=4$ならば$\vert a+1\vert \geqq 1$である。
(3)$ab$が有理数であるならば、a、bはともに有理数である。
(4)$a+b、ab$がともに有理数ならば、a、bはともに有理数である。
全体集合を$U$とし、条件$p、q$を満たす全体の集合を、それぞれ$P.Q$とする。
命題$p$(補集合)⇒$q$が真であるとき、$P、Q$について常に成り立つ事をすべて選べ。
①$P=Q$
②$Q⊂P$
③$Q$(補集合)$⊂P$
④$P⊂Q$(補集合)
⑤$P∪Q$(補集合)$=P$
⑥$P∪Q$(補集合)$=Q$(補集合)
⑦$P∩Q=∅$
⑧$P∪Q=U$
数と式 集合の考え方【いつものシミズ君がていねいに解説】

単元:
#数Ⅰ#数と式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$U={1,2,3,4,5,6,7,8,9}$を全体集合とする。$U$の部分集合A、Bについて
$A∩B={2}$ $A$(補集合)$∩B={4,6,8}$ $A$(補集合)$∩B$(補集合)$={1.9}$
であるとき、次の$∩$を求めよ。
(1)$A∪B$
(2)$B$
(3)$A∩B$(補集合)
$U={x|1≦x≦10、xは整数}$を全体集合とする。$U$の部分集合
$A={1,2,3,4,8},B={3,4,5,6},C{2,3,6,7}$
について、次の集合を求めよ。
(1)$A∩B∩C$
(2)$A∪B∪C$
(3)$A∩B∩C$(補集合)
(4)$A$(補集合)$∩B∩C$(補集合)
(5)$(A∩B∩C)$(補集合)
(6)$(A∪C)∩B$(補集合)
$A={1、3、3a-2}$, $B={-5、a+2、a^2-2a+1}$,$A∩B={1、4}$のとき
定数aの値と和集合$A∪B$を求めよ。
この動画を見る
$U={1,2,3,4,5,6,7,8,9}$を全体集合とする。$U$の部分集合A、Bについて
$A∩B={2}$ $A$(補集合)$∩B={4,6,8}$ $A$(補集合)$∩B$(補集合)$={1.9}$
であるとき、次の$∩$を求めよ。
(1)$A∪B$
(2)$B$
(3)$A∩B$(補集合)
$U={x|1≦x≦10、xは整数}$を全体集合とする。$U$の部分集合
$A={1,2,3,4,8},B={3,4,5,6},C{2,3,6,7}$
について、次の集合を求めよ。
(1)$A∩B∩C$
(2)$A∪B∪C$
(3)$A∩B∩C$(補集合)
(4)$A$(補集合)$∩B∩C$(補集合)
(5)$(A∩B∩C)$(補集合)
(6)$(A∪C)∩B$(補集合)
$A={1、3、3a-2}$, $B={-5、a+2、a^2-2a+1}$,$A∩B={1、4}$のとき
定数aの値と和集合$A∪B$を求めよ。
図形の性質 作図問題【TAKAHASHI名人がていねいに解説】

単元:
#数A#図形の性質#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
線分ABが与えられたとき, 線分ABを斜辺とし, $\angle BAC=60°$ である直角三角形ABC を作図せよ。
右の図のような円があり,その周上に点Aがある。
Aを頂点の1つとし、他の5つの頂点がいずれもこの円周上にあるような正六角形を作図せよ。
右の図のように,直線と円Oおよびその中心が与えられている。
直線lに平行な円Oの接線を作図せよ。
この動画を見る
線分ABが与えられたとき, 線分ABを斜辺とし, $\angle BAC=60°$ である直角三角形ABC を作図せよ。
右の図のような円があり,その周上に点Aがある。
Aを頂点の1つとし、他の5つの頂点がいずれもこの円周上にあるような正六角形を作図せよ。
右の図のように,直線と円Oおよびその中心が与えられている。
直線lに平行な円Oの接線を作図せよ。
図形の性質 方べきの定理【TAKAHASHI名人がていねいに解説】
単元:
#数A#図形の性質#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
■問題文
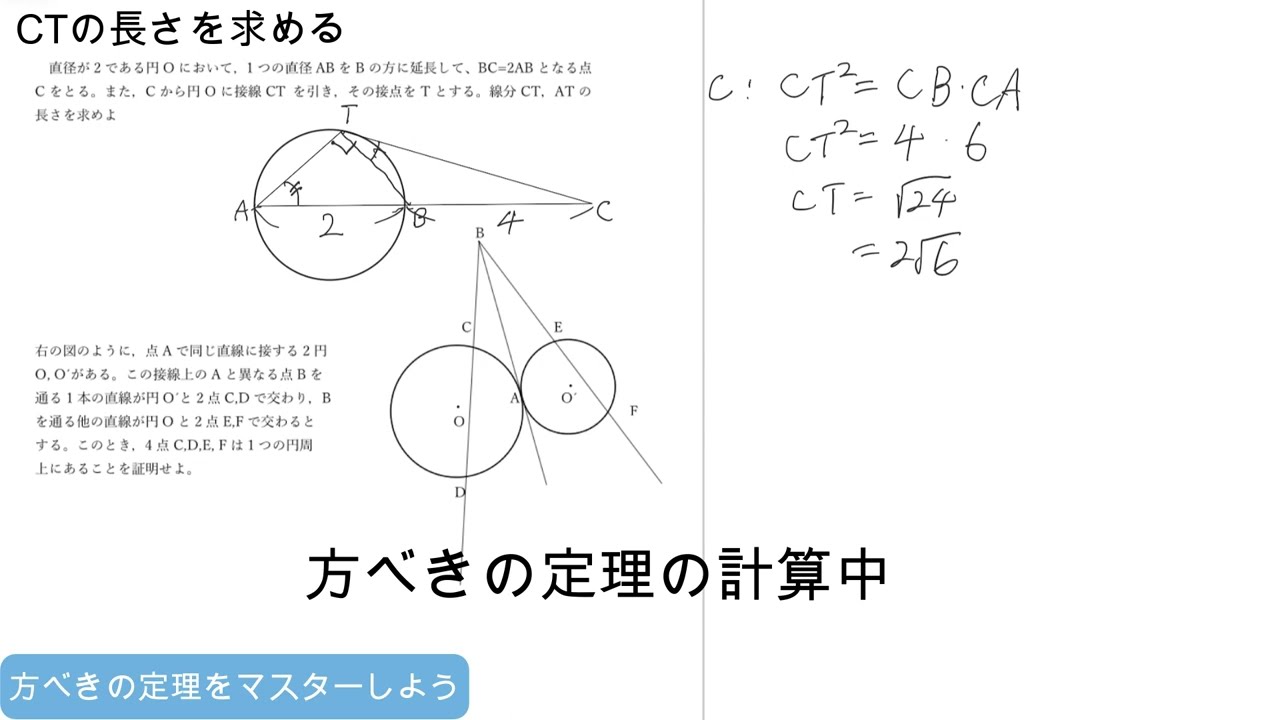
直径が2である円Oにおいて、1つの直径ABをBの方に延長して、BC=2ABとなる点Cをとる。また、Cから円Oに接線CTを引き、その接点をTとする。線分CT,ATの長さを求めよ。
右の図のように、点Aで同じ直線に接する2円O、O´がある。
この接線上のAと異なる点Bを通る1本の直線が円Oと2点C,Dで交わり, Bを通る他の直線が円 O′と2点E,Fで交わるとする。このとき, 4点 C, D, E, F は1つの円周上にあることを証明せよ。
この動画を見る
■問題文
直径が2である円Oにおいて、1つの直径ABをBの方に延長して、BC=2ABとなる点Cをとる。また、Cから円Oに接線CTを引き、その接点をTとする。線分CT,ATの長さを求めよ。
右の図のように、点Aで同じ直線に接する2円O、O´がある。
この接線上のAと異なる点Bを通る1本の直線が円Oと2点C,Dで交わり, Bを通る他の直線が円 O′と2点E,Fで交わるとする。このとき, 4点 C, D, E, F は1つの円周上にあることを証明せよ。
数と式 式の展開②【化学のタカシーがていねいに解説】

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
展開せよ
$(a+1)^3$ $(x+3y)^3$
$(2a-1)^3$ $(-3a+2b)^3$
展開せよ
$(a+5)(a^2-5a+25)$
$(3-a)(9+3a+a^2)$
$(2x+y)(4x^2-2xy+y^2)$
$(3a-2b)(9a^2+6ab+4b^2)$
計算せよ
$(x-1)(x-3)(x+1)(x+3)$ $(x+2)(x+5)(x-4)(x-1)$
$(a-b)(a+b)(a+b)(a+b)$ $(2x-y)^3(2x+y)^3$
$(a+b)^2(a-b)^2(a+ab+b)^2(a-ab+b)^2$
$(x+2)(x-2)(x^2+2x+4)(x^2-2x+4)$
$(a+b+c)^2+(a+b-c)^2+(b+c-a)^2+(c+a-b)^2$
この動画を見る
展開せよ
$(a+1)^3$ $(x+3y)^3$
$(2a-1)^3$ $(-3a+2b)^3$
展開せよ
$(a+5)(a^2-5a+25)$
$(3-a)(9+3a+a^2)$
$(2x+y)(4x^2-2xy+y^2)$
$(3a-2b)(9a^2+6ab+4b^2)$
計算せよ
$(x-1)(x-3)(x+1)(x+3)$ $(x+2)(x+5)(x-4)(x-1)$
$(a-b)(a+b)(a+b)(a+b)$ $(2x-y)^3(2x+y)^3$
$(a+b)^2(a-b)^2(a+ab+b)^2(a-ab+b)^2$
$(x+2)(x-2)(x^2+2x+4)(x^2-2x+4)$
$(a+b+c)^2+(a+b-c)^2+(b+c-a)^2+(c+a-b)^2$
数と式 式の展開①【化学のタカシーがていねいに解説】

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
[ ]内の文字について降べきの順に整理せよ
$ax^2+bx-x^4+ax^2-ab [x]$
$2x^2+y^2-3xy-2y^2+3y+4xy-x^2-2x-5 [y]$
$ax^3+a^2x-2x^2-a^3-3ax^3+4a^3 [a]$
$a^2b+b^3+abc-a^2c-ac^2+bc^2-ab^2+c^3 [a]$
ある多項式から$3x^2-xy+2y^2$を引くところ
を誤って加えたため,答えが$2x^2+xy-y^2$
となった。正しい答えを求めよ
次の式を展開した時の[ ]内の項の係数を
求めよ
$(5a^3-3a^2b+7ab^2-2b^3)(3a^2+2ab-3b^2)[a^2b^3][a^3b^2]$
$(x+2y-z)(3x+4y+2z)(-x+y-3z)[xy^2][xyz]$
この動画を見る
[ ]内の文字について降べきの順に整理せよ
$ax^2+bx-x^4+ax^2-ab [x]$
$2x^2+y^2-3xy-2y^2+3y+4xy-x^2-2x-5 [y]$
$ax^3+a^2x-2x^2-a^3-3ax^3+4a^3 [a]$
$a^2b+b^3+abc-a^2c-ac^2+bc^2-ab^2+c^3 [a]$
ある多項式から$3x^2-xy+2y^2$を引くところ
を誤って加えたため,答えが$2x^2+xy-y^2$
となった。正しい答えを求めよ
次の式を展開した時の[ ]内の項の係数を
求めよ
$(5a^3-3a^2b+7ab^2-2b^3)(3a^2+2ab-3b^2)[a^2b^3][a^3b^2]$
$(x+2y-z)(3x+4y+2z)(-x+y-3z)[xy^2][xyz]$
図形と計量 多角形【NI・SHI・NOがていねいに解説】
単元:
#数Ⅰ#図形と計量#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
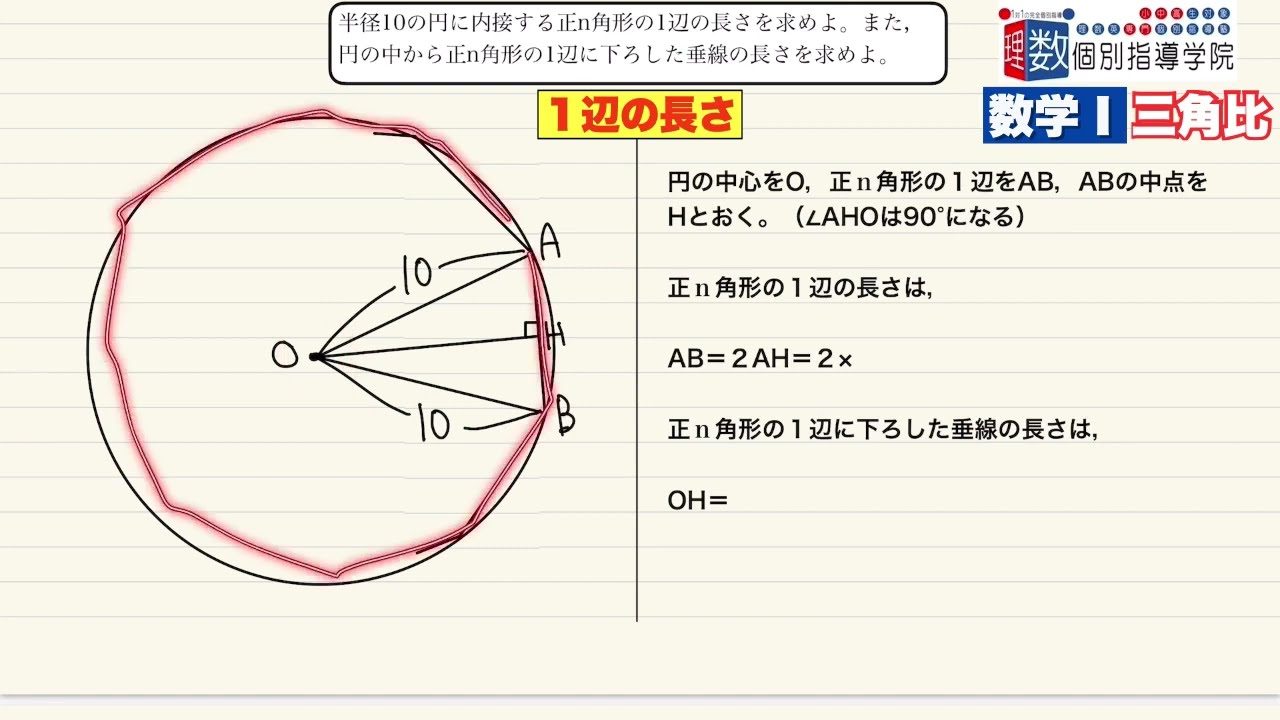
半径10の円に内接する正n角形の1辺の長さを求めよ。また,円の中心から正n角形の1辺に下ろした垂線の長さを求めよ。
この動画を見る
半径10の円に内接する正n角形の1辺の長さを求めよ。また,円の中心から正n角形の1辺に下ろした垂線の長さを求めよ。
図形と計量 三角比応用 二か所からの測量【NI・SHI・NOがていねいに解説】
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
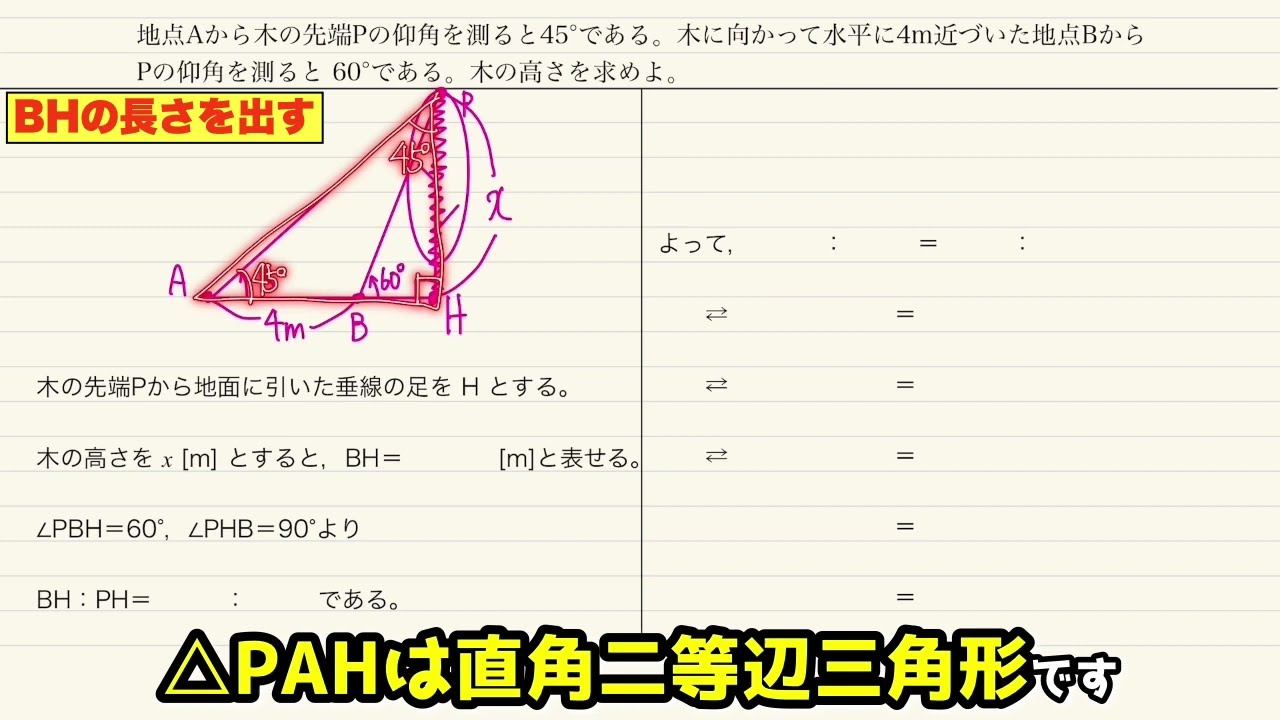
$\angle C=90°$ である直角三角形ABCにおいて,$\angle A=\theta, AB=k$ とする。頂点Cから辺ABに下ろした垂線を CD とするとき,次の線分の長さを$k,\theta$を用いて表せ。(1) $BC$ (2) $AC$ (3) $AD$ (4) $CD$ (5) $BD$
この動画を見る
$\angle C=90°$ である直角三角形ABCにおいて,$\angle A=\theta, AB=k$ とする。頂点Cから辺ABに下ろした垂線を CD とするとき,次の線分の長さを$k,\theta$を用いて表せ。(1) $BC$ (2) $AC$ (3) $AD$ (4) $CD$ (5) $BD$
場合の数と確率 確率基本①【教えて鈴木先生がていねいに解説】

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
A,B,C,D,E,F,G,Hの8文字を無造作に1列に並べるとき、次のようになる確率を求めよ。
(1)両端がA,Bである。
(2)A,Bが隣り合う。
(3)AはBより左に、BはCより左にある。
男子6人、女子2人がくじ引きで席を決めて円卓を囲んで座るとき、次のようになる確率を求めよ。
(1)女子2人が隣り合う。
(2)女子2人が向かい合う。
A,B,C,Dの4人がじゃんけんを1回するとき、次の確率を求めよ。
(1)Aだけが勝つ確率
(2)1人だけが勝つ確率
3つのさいころを同時に投げるとき、次のような目が出る確率を求めよ。
(1)目の積が150
(2)目の積が18
(3)目の積が135以上
この動画を見る
A,B,C,D,E,F,G,Hの8文字を無造作に1列に並べるとき、次のようになる確率を求めよ。
(1)両端がA,Bである。
(2)A,Bが隣り合う。
(3)AはBより左に、BはCより左にある。
男子6人、女子2人がくじ引きで席を決めて円卓を囲んで座るとき、次のようになる確率を求めよ。
(1)女子2人が隣り合う。
(2)女子2人が向かい合う。
A,B,C,Dの4人がじゃんけんを1回するとき、次の確率を求めよ。
(1)Aだけが勝つ確率
(2)1人だけが勝つ確率
3つのさいころを同時に投げるとき、次のような目が出る確率を求めよ。
(1)目の積が150
(2)目の積が18
(3)目の積が135以上
2次関数の決定【野本さんちのツトムくんがていねいに解説】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
172 次の条件を満たすような放物線の方程式を求めよ。
(1) 放物線 $y=-3x^2+x-1$を平行移動した曲線で,頂点が点(-2,3)である。
(2) 放物線$y=x^2-3x$を平行移動した曲線で,2点 (2,1),(4,5)を通る。
173 2つの放物線$y=x^2-3x, y=\dfrac{1}{2}x^2+ax+b$の頂点が一致するように,定数a,bの値を定めよ。
174(1) 放物線$y=x^2-3x+4$を平行移動した曲線で,点(2, 4)を通り,頂点が直線$y=2x+1$上にある放物線の方程式を求めよ。
(2) 放物線$y=-2x^2+5x$を平行移動した曲線で,点(1, -3)を通り,頂点が放物線$y=x^2+4$上にある放物線の方程式を求めよ。
この動画を見る
172 次の条件を満たすような放物線の方程式を求めよ。
(1) 放物線 $y=-3x^2+x-1$を平行移動した曲線で,頂点が点(-2,3)である。
(2) 放物線$y=x^2-3x$を平行移動した曲線で,2点 (2,1),(4,5)を通る。
173 2つの放物線$y=x^2-3x, y=\dfrac{1}{2}x^2+ax+b$の頂点が一致するように,定数a,bの値を定めよ。
174(1) 放物線$y=x^2-3x+4$を平行移動した曲線で,点(2, 4)を通り,頂点が直線$y=2x+1$上にある放物線の方程式を求めよ。
(2) 放物線$y=-2x^2+5x$を平行移動した曲線で,点(1, -3)を通り,頂点が放物線$y=x^2+4$上にある放物線の方程式を求めよ。
2次関数の最大と最小条件式つき【野本さんちのツトムくんがていねいに解説】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1) $2x+y=1$のとき,$x^2+y^2$の最小値を求めよ。
(2) $x+2y+3=0$のとき,$xy$の最大値を求めよ。
$x\geqq O, y\geqq O, x+y=4$のとき,xのとりうる値の範囲を求めよ。また、$x^2+2y^2$の最大値と最小値を求めよ。
この動画を見る
(1) $2x+y=1$のとき,$x^2+y^2$の最小値を求めよ。
(2) $x+2y+3=0$のとき,$xy$の最大値を求めよ。
$x\geqq O, y\geqq O, x+y=4$のとき,xのとりうる値の範囲を求めよ。また、$x^2+2y^2$の最大値と最小値を求めよ。
しまだじろうが自分の教え子に英単語アプリ「でた単」を薦める理由(オンライン授業切り抜き)

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#英単語
指導講師:
理数個別チャンネル
問題文全文(内容文):
しまだじろうが自分の教え子に英単語アプリ「でた単」を薦める理由に関して解説していきます.
この動画を見る
しまだじろうが自分の教え子に英単語アプリ「でた単」を薦める理由に関して解説していきます.
Lesson5-2 NT Stage1 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(中学生)#中1英語#Where、Which、Howで始まる疑問文
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson5#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. SERIES Third Edition Stage1 Lesson 5-1のKey Point解説
この動画を見る
N.T. SERIES Third Edition Stage1 Lesson 5-1のKey Point解説
Lesson5-2 ニュートレジャー Stage1 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(中学生)#中2英語#Whで始まる疑問文、Howで始まる疑問文、付加疑問文、否定疑問文
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage1 3rd Edition Lesson 5-1のKey Point解説していきます.
この動画を見る
ニュートレジャー Stage1 3rd Edition Lesson 5-1のKey Point解説していきます.
Lesson5-1 NT Stage1 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(中学生)#中1英語#代名詞の目的格、所有代名詞、Whose~?と答え方
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson5#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. SERIES Third Edition Stage1 Lesson 5-1のKey Point解説
この動画を見る
N.T. SERIES Third Edition Stage1 Lesson 5-1のKey Point解説
Lesson5-1 ニュートレジャー Stage1 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(中学生)#中2英語#人称代名詞、所有代名詞、再帰代名詞、itの特別用法、指示代名詞、不定代名詞
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage1 3rd Edition Lesson 5-1のKey Point解説していきます.
この動画を見る
ニュートレジャー Stage1 3rd Edition Lesson 5-1のKey Point解説していきます.
データの分析 欠けたデータの推測【ユースケ・マセマティックがていねいに解説】

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のデータは、ある8店舗での1kgあたりのみかんの価格である。ただし、aの値は0以上の整数である。
525 550 498 550 555 500 a (単位は円)
(1)aの値がわからないとき、このデータの中央値として何通りの値があり得るか。
(2)このデータの平均値が535円であるとき、このデータの中央値を求めよ。
この動画を見る
次のデータは、ある8店舗での1kgあたりのみかんの価格である。ただし、aの値は0以上の整数である。
525 550 498 550 555 500 a (単位は円)
(1)aの値がわからないとき、このデータの中央値として何通りの値があり得るか。
(2)このデータの平均値が535円であるとき、このデータの中央値を求めよ。
データの分析 データの中に誤りがあった場合【ユースケ・マセマティックがていねいに解説】

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある高校で、エコ活動としてペットボトルのキャップを集めている。次のデータは、1か月ごとに集まったキャップの重量を半年間記録したものである。
3.2 1.2 2.3 2.0 2.7 2.4 (単位はkg)
(1)中央値と平均値を求めよ。
(2)上記の6個のうち1個が誤りであることが分かった。正しい数値に基づく中央値と平均値は、それぞれ2.55kgと2.4kgであるという。誤っている数値を選び、正しい数値を求めよ。
この動画を見る
ある高校で、エコ活動としてペットボトルのキャップを集めている。次のデータは、1か月ごとに集まったキャップの重量を半年間記録したものである。
3.2 1.2 2.3 2.0 2.7 2.4 (単位はkg)
(1)中央値と平均値を求めよ。
(2)上記の6個のうち1個が誤りであることが分かった。正しい数値に基づく中央値と平均値は、それぞれ2.55kgと2.4kgであるという。誤っている数値を選び、正しい数値を求めよ。
データの分析 度数分布表【ユースケ・マセマティックがていねいに解説】

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の表は25人の生徒のテストの得点のデータから作った度数分布表である。
(1)このデータの平均値のとり得る範囲を求めよ。
(2)60点以上69点以下の階級に含まれる値が次ののようであるとき、全体のデータの中央値を求めよ。
68 63 66 62 68 63 67 65
この動画を見る
右の表は25人の生徒のテストの得点のデータから作った度数分布表である。
(1)このデータの平均値のとり得る範囲を求めよ。
(2)60点以上69点以下の階級に含まれる値が次ののようであるとき、全体のデータの中央値を求めよ。
68 63 66 62 68 63 67 65




