 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【受験算数】仕事算(基本❹)ニュートン算【予習シリーズ演習問題集・小5下】

単元:
#算数(中学受験)#文章題#仕事算とニュートン算
教材:
#予習シ#予習シ演問・小5下#中学受験教材#仕事算
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある動物園では、開場時刻にすでに400人の行列ができていて、その後も1分間に10人の割合でこの行列に人が加わります。3か所の入口を開いたところ80分で行列がなくなりました。これについて、次の問いに答えなさい。
(1)1か所の入口から1分間に何人の割合で人が入りましたか。
(2)20分以内に行列をなくすためには、最低何か所の入口を開けばよいですか。
この動画を見る
ある動物園では、開場時刻にすでに400人の行列ができていて、その後も1分間に10人の割合でこの行列に人が加わります。3か所の入口を開いたところ80分で行列がなくなりました。これについて、次の問いに答えなさい。
(1)1か所の入口から1分間に何人の割合で人が入りましたか。
(2)20分以内に行列をなくすためには、最低何か所の入口を開けばよいですか。
【受験算数】仕事算(基本❸)日数と仕事量は逆比【予習シリーズ演習問題集・小5下】

単元:
#算数(中学受験)#文章題#仕事算とニュートン算
教材:
#予習シ#予習シ演問・小5下#中学受験教材#仕事算
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある仕事をするのに、A1人ですると24日かかります。この仕事をA1人で16日した後、残りをB1人だけでしたところ12日かかりました。これについて、次の問いに答えなさい。
(1)A、Bが1日にする仕事量の比を求めなさい。
(2)この仕事をAとBの2人で一緒に始めましたが、途中でBが4日間休みました。仕事を終えるのに全部で何日かかりましたか。
この動画を見る
ある仕事をするのに、A1人ですると24日かかります。この仕事をA1人で16日した後、残りをB1人だけでしたところ12日かかりました。これについて、次の問いに答えなさい。
(1)A、Bが1日にする仕事量の比を求めなさい。
(2)この仕事をAとBの2人で一緒に始めましたが、途中でBが4日間休みました。仕事を終えるのに全部で何日かかりましたか。
【受験算数】仕事算(基本❷)仕事算とつるかめ算【予習シリーズ演習問題集・小5下】

単元:
#算数(中学受験)#文章題#仕事算とニュートン算
教材:
#予習シ#予習シ演問・小5下#中学受験教材#仕事算
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある空の水そうに水を入れていっぱいにするのに、A管だけを使うと45分かかり、A管とB管を一緒に使うと20分かかります。これについて、次の問いに答えなさい。
(1)B管だけを使うと、この水そうをいっぱいにするのに何分かかりますか。
(2)この水そうに、はじめA管だけで水をいれ、途中でA管を閉じて、残りをB管だけで入れたところ、水を入れ始めてから42分後に水そうはいっぱいになりました。A管だけで水を入れていた時間は何分ですか。
この動画を見る
ある空の水そうに水を入れていっぱいにするのに、A管だけを使うと45分かかり、A管とB管を一緒に使うと20分かかります。これについて、次の問いに答えなさい。
(1)B管だけを使うと、この水そうをいっぱいにするのに何分かかりますか。
(2)この水そうに、はじめA管だけで水をいれ、途中でA管を閉じて、残りをB管だけで入れたところ、水を入れ始めてから42分後に水そうはいっぱいになりました。A管だけで水を入れていた時間は何分ですか。
【数学】2022年度神奈川県立高校入試数学大問5イ別解

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
大,小2つのさいころを同時に1回投げ,大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとする。出た目の数によって,線分PQ上に点Rを,PR:RQ=a:bとなるようにとり,線分PRを1辺とする正方形をX,線分RQを1辺とする正方形をYとし,この2つの正方形の面積を比較する。
(イ) Xの面積がYの面積より25cm²以上大きくなる確率は□である。
この動画を見る
大,小2つのさいころを同時に1回投げ,大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとする。出た目の数によって,線分PQ上に点Rを,PR:RQ=a:bとなるようにとり,線分PRを1辺とする正方形をX,線分RQを1辺とする正方形をYとし,この2つの正方形の面積を比較する。
(イ) Xの面積がYの面積より25cm²以上大きくなる確率は□である。
【中学数学】高校入試:2022年度神奈川県立高校入試数学大問5イ別解

単元:
#数学(中学生)#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#高校入試過去問(数学)#神奈川県公立高校入試#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
大,小2つのさいころを同時に1回投げ,大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとする。出た目の数によって,線分PQ上に点Rを,PR:RQ=a:bとなるようにとり,線分PRを1辺とする正方形をX,線分RQを1辺とする正方形をYとし,この2つの正方形の面積を比較する。
(イ) Xの面積がYの面積より25cm²以上大きくなる確率は□である。
この動画を見る
大,小2つのさいころを同時に1回投げ,大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとする。出た目の数によって,線分PQ上に点Rを,PR:RQ=a:bとなるようにとり,線分PRを1辺とする正方形をX,線分RQを1辺とする正方形をYとし,この2つの正方形の面積を比較する。
(イ) Xの面積がYの面積より25cm²以上大きくなる確率は□である。
【英検2級解答速報第三弾】2021年版のテンプレを当てはめて解いてみた。

単元:
#英語(高校生)#英作文#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級#自由英作文
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題文
Some people say that Japan should use the Internet for people to vote in elections.
Do you agree with this opinion?
●convenience ●cost ●security
テンプレの元の動画
【英検2級】ライティングで満点狙える神技を期間限定公開〜2021最新版
https://youtu.be/5TEhhYbStXw
訂正
最後の文にピリオドを忘れています!すいません。
この動画を見る
問題文
Some people say that Japan should use the Internet for people to vote in elections.
Do you agree with this opinion?
●convenience ●cost ●security
テンプレの元の動画
【英検2級】ライティングで満点狙える神技を期間限定公開〜2021最新版
https://youtu.be/5TEhhYbStXw
訂正
最後の文にピリオドを忘れています!すいません。
【英検2級】2023年1月22日(日)のライティング問題に2021年版のテンプレを当てはめて解いてみた。【日本最速解答速報】

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級
指導講師:
理数個別チャンネル
問題文全文(内容文):
Some people say that Japan should use the Internet for people to vote in elections.
Do you agree with this opinion?
●convenience ●cost ●security
この動画を見る
Some people say that Japan should use the Internet for people to vote in elections.
Do you agree with this opinion?
●convenience ●cost ●security
【英検2級解答速報第二弾】このテンプレ動画を見てた人は今回の英検ライティングは楽勝だったんじゃない?

単元:
#英語(高校生)#英作文#英検#英検2級#自由英作文
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題文
Some people say that Japan should use the Internet for people to vote in elections.
Do you agree with this opinion?
●convenience ●cost ●security
テンプレの元の動画
【英検2級ライティング】10分で8割、15分で満点狙える最新テンプレート
https://youtu.be/QOZ0G138ry0
この動画を見る
問題文
Some people say that Japan should use the Internet for people to vote in elections.
Do you agree with this opinion?
●convenience ●cost ●security
テンプレの元の動画
【英検2級ライティング】10分で8割、15分で満点狙える最新テンプレート
https://youtu.be/QOZ0G138ry0
【的中!楽勝!】2023年1月22日(日)の英検2級ライティング問題に最新テンプレを当てはめて解いてみた。【日本最速解答速報】

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級
指導講師:
理数個別チャンネル
問題文全文(内容文):
Some people say that Japan should use the Internet for people to vote in elections.
Do you agree with this opinion?
●convenience ●cost ●security
この動画を見る
Some people say that Japan should use the Internet for people to vote in elections.
Do you agree with this opinion?
●convenience ●cost ●security
【英検2級解答速報第一弾】2年前のテンプレ動画に今日の英検2級ライティング問題を当てはめてみた。

単元:
#英語(高校生)#英作文#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級#自由英作文
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題文
Some people say that Japan should use the Internet for people to vote in elections.
Do you agree with this opinion?
●convenience ●cost ●security
テンプレの元の動画
【英検2級】ライティング9割をもぎとるチート技公開
https://youtu.be/ztwpk5TcRVc
この動画を見る
問題文
Some people say that Japan should use the Internet for people to vote in elections.
Do you agree with this opinion?
●convenience ●cost ●security
テンプレの元の動画
【英検2級】ライティング9割をもぎとるチート技公開
https://youtu.be/ztwpk5TcRVc
【英検2級】 2023年1月22日(日)のライティング問題に 2年前のテンプレ動画を当てはめて解いてみた。【日本最速解答速報】

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級
指導講師:
理数個別チャンネル
問題文全文(内容文):
Some people say that Japan should use the Internet for people to vote in elections.
Do you agree with this opinion?
●convenience ●cost ●security
この動画を見る
Some people say that Japan should use the Internet for people to vote in elections.
Do you agree with this opinion?
●convenience ●cost ●security
【解答速報】2023年1月22日(日)英検準2級ライティング解答例と考え方を紹介します。

単元:
#英語(高校生)#英作文#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検準2級#自由英作文
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題文
Do you think libraries should have more book events for children?
テンプレ元の動画
【英検準2級】ライティング満点を楽勝に取れる直前講座
https://youtu.be/UfD2-zP2aKQ
【保護者・教員向け】英検準2級合格のための教科書(リーディング5割やリスニングが4割でも合格した実例紹介/具体的なライティングテンプレを過去問3年分紹介)
https://youtu.be/cxYhUrOcoX0
この動画を見る
問題文
Do you think libraries should have more book events for children?
テンプレ元の動画
【英検準2級】ライティング満点を楽勝に取れる直前講座
https://youtu.be/UfD2-zP2aKQ
【保護者・教員向け】英検準2級合格のための教科書(リーディング5割やリスニングが4割でも合格した実例紹介/具体的なライティングテンプレを過去問3年分紹介)
https://youtu.be/cxYhUrOcoX0
【数B】ベクトル:ベクトルの基本⑲空間ベクトルにおける三角形の面積

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
3点A$(-2,1,3),B=(-3,1,4),C=(-3,3,5)$が与えられたとき、三角形ABCの面積を求めよ
この動画を見る
3点A$(-2,1,3),B=(-3,1,4),C=(-3,3,5)$が与えられたとき、三角形ABCの面積を求めよ
【数C】ベクトルの基本⑲空間ベクトルにおける三角形の面積

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#チャート式#青チャートⅡ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
3点A(-2,1,3),B=(-3,1,4),C=(-3,3,5)が与えられたとき、三角形ABCの面積を求めよ
この動画を見る
3点A(-2,1,3),B=(-3,1,4),C=(-3,3,5)が与えられたとき、三角形ABCの面積を求めよ
【日本最速解答速報】 2023年1月22日(日)英検準2級ライティング解答例と考え方を紹介します。

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検準2級
指導講師:
理数個別チャンネル
問題文全文(内容文):
Do you think libraries should have more book events for children?
この動画を見る
Do you think libraries should have more book events for children?
【速報】今日の英検2級ライティングはインターネット投票の問題だったと聞きました。

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級
指導講師:
理数個別チャンネル
問題文全文(内容文):
今日の英検2級ライティングはインターネット投票の問題だったと聞きました.
この動画を見る
今日の英検2級ライティングはインターネット投票の問題だったと聞きました.
2023年1月22日(日)英検準2級ライティング添削コメント紹介 #shorts #英検準2級
単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検準2級
指導講師:
理数個別チャンネル
問題文全文(内容文):
英検準2級ライティング添削コメント紹介していきます.
この動画を見る
英検準2級ライティング添削コメント紹介していきます.
【化学】入試直前用!合金は語呂で覚えよう!(一気見用)

単元:
#化学#無機#典型金属元素の単体と化合物#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
入試直前、定期試験直前用!
合金を語呂合わせで紹介。
ジュラルミン・ステンレス・白銅・黄銅・ブロンズ・はんだの覚え方を3分で紹介しています。覚えれば得点源になる、けど・・・なかなか覚えられない・・・そんな人は語呂で覚えていきましょう!
この動画を見る
入試直前、定期試験直前用!
合金を語呂合わせで紹介。
ジュラルミン・ステンレス・白銅・黄銅・ブロンズ・はんだの覚え方を3分で紹介しています。覚えれば得点源になる、けど・・・なかなか覚えられない・・・そんな人は語呂で覚えていきましょう!
【化学】合金③ 入試直前用!合金は語呂で覚えよう!

単元:
#化学#無機#典型金属元素の単体と化合物#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
入試直前や定期試験直前用。
青銅(ブロンズ)とはんだの覚え方を語呂合わせで紹介!
この動画を見る
入試直前や定期試験直前用。
青銅(ブロンズ)とはんだの覚え方を語呂合わせで紹介!
【化学】合金② 入試直前用!合金は語呂で覚えよう!

単元:
#化学#無機#典型金属元素の単体と化合物#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
入試直前や定期試験直前に見てください。
白銅と黄銅の覚え方を語呂合わせで紹介。
この動画を見る
入試直前や定期試験直前に見てください。
白銅と黄銅の覚え方を語呂合わせで紹介。
【化学】合金① 入試直前用!合金は語呂で覚えよう!

単元:
#化学#無機#典型金属元素の単体と化合物#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
合金は覚えれば即得点につながります。入試直前や定期試験直前に見返す用です。
3つの金属の合金であるジュラルミンとステンレスの覚え方を語呂合わせで紹介をしています。
この動画を見る
合金は覚えれば即得点につながります。入試直前や定期試験直前に見返す用です。
3つの金属の合金であるジュラルミンとステンレスの覚え方を語呂合わせで紹介をしています。
【受験算数】平面図形:三角形の中にある三角形②【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#平面図形#平面図形その他
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図の点D,E,Fは、三角形ABCの各辺をそれぞれ延長した直線上にあり、
AB:BD=2:3
BC:CE=1:2
CA:AF=1:3
です。このとき、次の比を求めなさい。
(1)三角形ABCと三角形BDEの面積の比
(2)三角形ABCと三角形DEFの面積の比
この動画を見る
右の図の点D,E,Fは、三角形ABCの各辺をそれぞれ延長した直線上にあり、
AB:BD=2:3
BC:CE=1:2
CA:AF=1:3
です。このとき、次の比を求めなさい。
(1)三角形ABCと三角形BDEの面積の比
(2)三角形ABCと三角形DEFの面積の比
【受験算数】三角形の中にある三角形②【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#平面図形#角度と面積
教材:
#予習シ#予習シ算数・小5下#中学受験教材#平面図形と比
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図の点D,E,Fは、三角形ABCの各辺をそれぞれ延長した直線上にあり、
AB:BD=2:3
BC:CE=1:2
CA:AF=1:3
です。このとき、次の比を求めなさい。
(1)三角形ABCと三角形BDEの面積の比
(2)三角形ABCと三角形DEFの面積の比
この動画を見る
右の図の点D,E,Fは、三角形ABCの各辺をそれぞれ延長した直線上にあり、
AB:BD=2:3
BC:CE=1:2
CA:AF=1:3
です。このとき、次の比を求めなさい。
(1)三角形ABCと三角形BDEの面積の比
(2)三角形ABCと三角形DEFの面積の比
【化学】共通テスト2023大問1 解説

英検動画をご覧の皆様へ

【英語】句動詞:50音順に文法用語を解説する⑦

【英語】【句動詞】50音順に文法用語を解説する⑦

英検2級最新必勝テンプレ出来ました #英検2級 #英検 #shorts
【数学】2022年度神奈川県立高校入試数学大問5アイ

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
大,小2つのさいころを同時に1回投げ,大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとする。出た目の数によって,線分PQ上に点Rを,PR:RQ=a:bとなるようにとり,線分PRを1辺とする正方形をX,線分RQを1辺とする正方形をYとし,この2つの正方形の面積を比較する。
(ア) Xの面積とYの面積が等しくなる確率は□である。
(イ) Xの面積がYの面積より25cm²以上大きくなる確率は□である。
この動画を見る
大,小2つのさいころを同時に1回投げ,大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとする。出た目の数によって,線分PQ上に点Rを,PR:RQ=a:bとなるようにとり,線分PRを1辺とする正方形をX,線分RQを1辺とする正方形をYとし,この2つの正方形の面積を比較する。
(ア) Xの面積とYの面積が等しくなる確率は□である。
(イ) Xの面積がYの面積より25cm²以上大きくなる確率は□である。
【中学数学】高校入試:2022年度神奈川県立高校入試数学大問5アイ
単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
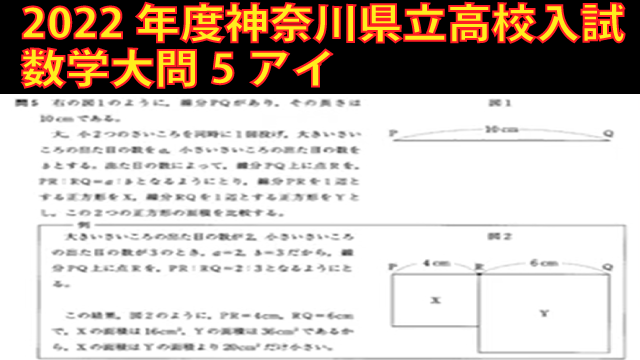
大,小2つのさいころを同時に1回投げ,大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとする。出た目の数によって,線分PQ上に点Rを,PR:RQ=a:bとなるようにとり,線分PRを1辺とする正方形をX,線分RQを1辺とする正方形をYとし,この2つの正方形の面積を比較する。
(ア) Xの面積とYの面積が等しくなる確率は□である。
(イ) Xの面積がYの面積より25cm²以上大きくなる確率は□である。
この動画を見る
大,小2つのさいころを同時に1回投げ,大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとする。出た目の数によって,線分PQ上に点Rを,PR:RQ=a:bとなるようにとり,線分PRを1辺とする正方形をX,線分RQを1辺とする正方形をYとし,この2つの正方形の面積を比較する。
(ア) Xの面積とYの面積が等しくなる確率は□である。
(イ) Xの面積がYの面積より25cm²以上大きくなる確率は□である。




