 渋谷教育学園渋谷中学
渋谷教育学園渋谷中学
 渋谷教育学園渋谷中学
渋谷教育学園渋谷中学
2025年渋谷教育学園渋谷中 面積 #中学受験 #算数 #渋渋 #面積

単元:
#算数(中学受験)#過去問解説(学校別)#渋谷教育学園渋谷中学
指導講師:
重吉
問題文全文(内容文):
(問)
下の図のような半径が10㎝の円があります。円周上の点は円周を12等分しています。
影のついた部分の面積は何㎠ですか。
※図は動画内参照
この動画を見る
(問)
下の図のような半径が10㎝の円があります。円周上の点は円周を12等分しています。
影のついた部分の面積は何㎠ですか。
※図は動画内参照
2025年渋谷教育学園渋谷中入試算数大問① 中学受験指導歴20年プロのじっくり解説

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題#過去問解説(学校別)#文章題#仕事算とニュートン算#平面図形#平面図形その他#速さ#速さその他#場合の数#場合の数#渋谷教育学園渋谷中学
指導講師:
重吉
問題文全文(内容文):
(1) \[
\frac{1}{2} + 7.15 \div \left( \frac{5}{7} - 1.875 \times \frac{2}{15} \right)
\]
(2) 渋男さんと教子さんは、駅から学校までジョギングをしました。駅と学校のちょうど真ん中に公園があります。2人は駅を同時に出発し、学校に同時に着きました。渋男さんは駅から公園までは時速8km、公園から学校までは時速12kmで走りました。救子さんは駅から学校まで一定の速さで走りました。教子さんの速さは時速何kmですか。
(3) 【A】はAの約数の個数を表します。例えば、6の約数は1.2.3.6なので 【6】=4です。
このとき、【【2025】×30】はいくつですか。
(4) A, B, C, D, E, F, G, H, I, J, Kの11人の生徒を5人部屋と6人部屋に分けます。 A, B, Cの3人の生徒が同じ部屋に入るとすると、11人の分け方は何通りありますか。
(5) 渋男さんと教子さんがある仕事をします。2人で一緒に行えば2時間で終わります。 同じ仕事を教子さんが1人で行うと、4時間30分で終わります。
ある日、同じ仕事を渋男さんと教子さんは9時から2人で一緒に始めました。9時40分に渋男さんは忘れ物に気づいて家へ帰りました。渋男さんがいない間、教子さんは1人で仕事をしました。渋男さんが戻ってきた後、渋男さんは1.2倍のスピードで、教子さんはこれまでと同じスピードで一緒に仕事を進めました。その結果、11時46分に終わりました。渋男さんが戻ってきたのは何時何分ですか。
(6) 下の図のような半径が10cmの円があります。円周上の点は円周を12等分しています。
影のついた部分の面積は何cmですか。
※図は動画内参照
この動画を見る
(1) \[
\frac{1}{2} + 7.15 \div \left( \frac{5}{7} - 1.875 \times \frac{2}{15} \right)
\]
(2) 渋男さんと教子さんは、駅から学校までジョギングをしました。駅と学校のちょうど真ん中に公園があります。2人は駅を同時に出発し、学校に同時に着きました。渋男さんは駅から公園までは時速8km、公園から学校までは時速12kmで走りました。救子さんは駅から学校まで一定の速さで走りました。教子さんの速さは時速何kmですか。
(3) 【A】はAの約数の個数を表します。例えば、6の約数は1.2.3.6なので 【6】=4です。
このとき、【【2025】×30】はいくつですか。
(4) A, B, C, D, E, F, G, H, I, J, Kの11人の生徒を5人部屋と6人部屋に分けます。 A, B, Cの3人の生徒が同じ部屋に入るとすると、11人の分け方は何通りありますか。
(5) 渋男さんと教子さんがある仕事をします。2人で一緒に行えば2時間で終わります。 同じ仕事を教子さんが1人で行うと、4時間30分で終わります。
ある日、同じ仕事を渋男さんと教子さんは9時から2人で一緒に始めました。9時40分に渋男さんは忘れ物に気づいて家へ帰りました。渋男さんがいない間、教子さんは1人で仕事をしました。渋男さんが戻ってきた後、渋男さんは1.2倍のスピードで、教子さんはこれまでと同じスピードで一緒に仕事を進めました。その結果、11時46分に終わりました。渋男さんが戻ってきたのは何時何分ですか。
(6) 下の図のような半径が10cmの円があります。円周上の点は円周を12等分しています。
影のついた部分の面積は何cmですか。
※図は動画内参照
2025年渋谷教育学園幕張中入試算数大問② 中学受験指導歴20年以上プロのじっくり解説

単元:
#算数(中学受験)#過去問解説(学校別)#渋谷教育学園渋谷中学#渋谷教育学園幕張中学校
指導講師:
重吉
問題文全文(内容文):
大問2
2つの数A.Bは、3.4.5.6.8.9のいずれかの数であり、異なるものとします。
4けたの数 A77Bをアとします。アの各位の数を、左から小さい順に並べかえて作った4けたの数をイとします。アからイを引いた数をウとします。例えば、 A = 6 、B = 5 とすると、ア=6775、イ=5677であり、ウ=1098 です。
次の各問いに答えなさい。
(1)ウとして考えられる最も大きな数を答えなさい。
(2)ウが2けたの数になるAとBの組は何通りありますか。
(3)ウが3けたの数になるAとBの組は何通りありますか。
この動画を見る
大問2
2つの数A.Bは、3.4.5.6.8.9のいずれかの数であり、異なるものとします。
4けたの数 A77Bをアとします。アの各位の数を、左から小さい順に並べかえて作った4けたの数をイとします。アからイを引いた数をウとします。例えば、 A = 6 、B = 5 とすると、ア=6775、イ=5677であり、ウ=1098 です。
次の各問いに答えなさい。
(1)ウとして考えられる最も大きな数を答えなさい。
(2)ウが2けたの数になるAとBの組は何通りありますか。
(3)ウが3けたの数になるAとBの組は何通りありますか。
2024年渋谷教育学園渋谷中算数大問②中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#立体図形#立体切断#渋谷教育学園渋谷中学
指導講師:
重吉
問題文全文(内容文):
2⃣図は動画内参照
図1は18個の立方体を積み上げて作った直方体です。図1の直方体を平面で切り、その後、 すべてバラバラにしたときの立体の個数を考えます。
例えば図1の直方体を3点ア、イ、ウを通る平面で切り、その後、すべてバラバラにすると、 9個の立方体と18個の切られた立体に分かれ、立体は合計で27個となります。 次の問いに答えなさい。
(1) 図1の直方体を3点イ、ウ、エを通る平面で切り、その後、すべてバラバラにすると、 立体は合計で何個になりますか。
図2は36個の立方体を積み上げて、直方体を作ったものです。
(2) 図2の直方体を3点A, B. Cを通る平面で切り、その後、すべてバラバラにすると、 立体は合計で何個になりますか。
(3) 図2の直方体を3点A、B、Dを通る平面で切り、その後、ずべてバラバラにすると、 立体は合計で何個になりますか。
この動画を見る
2⃣図は動画内参照
図1は18個の立方体を積み上げて作った直方体です。図1の直方体を平面で切り、その後、 すべてバラバラにしたときの立体の個数を考えます。
例えば図1の直方体を3点ア、イ、ウを通る平面で切り、その後、すべてバラバラにすると、 9個の立方体と18個の切られた立体に分かれ、立体は合計で27個となります。 次の問いに答えなさい。
(1) 図1の直方体を3点イ、ウ、エを通る平面で切り、その後、すべてバラバラにすると、 立体は合計で何個になりますか。
図2は36個の立方体を積み上げて、直方体を作ったものです。
(2) 図2の直方体を3点A, B. Cを通る平面で切り、その後、すべてバラバラにすると、 立体は合計で何個になりますか。
(3) 図2の直方体を3点A、B、Dを通る平面で切り、その後、ずべてバラバラにすると、 立体は合計で何個になりますか。
2024年渋谷教育学園渋谷中算数大問①(4)~(6)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#売買損益と食塩水#平面図形#角度と面積#相似と相似を利用した問題#立体図形#体積・表面積・回転体・水量・変化のグラフ#渋谷教育学園渋谷中学
指導講師:
重吉
問題文全文(内容文):
※図は動画内参照
(4)
下の図は二つの直角三角形からできています。影のついた部分を直線Lを軸として一回転させてできる立体の体積は何㎠ですか。
(5)
下の図は、円と正六角形と正十角形からできています。点Oは円の中心です。このとき、アの角の大きさは何度ですか。
(6)
容器Aには3 %の食塩水が600 g、容器Bには5 %の食塩水が300 g、容器Cには4 %の食塩水が入っています。A,B,Cから重さの比が1:2:2となるように食塩水を取り出し、空の容器Dに入れてよく混ぜ合わせました。Dの食塩水を3等分してA,B,Cにそれぞれ戻すと、Aの食塩水に溶けている食塩が22 gになりました。このときBの食塩水の濃さは何%になりますか。
この動画を見る
※図は動画内参照
(4)
下の図は二つの直角三角形からできています。影のついた部分を直線Lを軸として一回転させてできる立体の体積は何㎠ですか。
(5)
下の図は、円と正六角形と正十角形からできています。点Oは円の中心です。このとき、アの角の大きさは何度ですか。
(6)
容器Aには3 %の食塩水が600 g、容器Bには5 %の食塩水が300 g、容器Cには4 %の食塩水が入っています。A,B,Cから重さの比が1:2:2となるように食塩水を取り出し、空の容器Dに入れてよく混ぜ合わせました。Dの食塩水を3等分してA,B,Cにそれぞれ戻すと、Aの食塩水に溶けている食塩が22 gになりました。このときBの食塩水の濃さは何%になりますか。
2024年渋谷教育学園渋谷中算数大問①(4)~(6)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#文章題#売買損益と食塩水#平面図形#角度と面積#立体図形#体積・表面積・回転体・水量・変化のグラフ#渋谷教育学園渋谷中学
指導講師:
重吉
問題文全文(内容文):
※図は動画内参照図
(4)
下の図は2つの直角三角形からできています。影のついた部分を直線Lを軸として1回転させてできる立体の体積は何㎤ですか。
(5)
下の図は、円と正六角形と正十角形からできています。点Oは円の中心です。このとき㋐の角の大きさは何度ですか。
(6)
容器Aには3 %の食塩水が600 g、容器Bには5 %の食塩水が300 g、容器Cには4 %の食塩水が入っています。A,B,Cから重さの比が1:2:2となるように食塩水を取り出し、空の容器Dに入れてよく混ぜ合わせました。Dの食塩水を3等分してA,B,Cにそれぞれ戻すと、Aの食塩水に溶けている食塩が22 gになりました。このときBの食塩水の濃さは何%になりましたか。
この動画を見る
※図は動画内参照図
(4)
下の図は2つの直角三角形からできています。影のついた部分を直線Lを軸として1回転させてできる立体の体積は何㎤ですか。
(5)
下の図は、円と正六角形と正十角形からできています。点Oは円の中心です。このとき㋐の角の大きさは何度ですか。
(6)
容器Aには3 %の食塩水が600 g、容器Bには5 %の食塩水が300 g、容器Cには4 %の食塩水が入っています。A,B,Cから重さの比が1:2:2となるように食塩水を取り出し、空の容器Dに入れてよく混ぜ合わせました。Dの食塩水を3等分してA,B,Cにそれぞれ戻すと、Aの食塩水に溶けている食塩が22 gになりました。このときBの食塩水の濃さは何%になりましたか。
2024年渋谷教育学園渋谷中算数大問①(1)~(3)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数の性質その他#約数・倍数を利用する問題#過去問解説(学校別)#渋谷教育学園渋谷中学
指導講師:
重吉
問題文全文(内容文):
(1)
$1-0.625\div(20\dfrac{1}{24}\div20)\times(\dfrac{1}{12}-0.04)$を計算しなさい。
(2)
1から100までの100個の整数のうち、3でも7でも割り切れない偶数は何個ありますか。
(3)
【A】は整数Aを2で割り、その商を2で割っていき、商が1になるまで続けたときの2で割った数を表しています。
例えば、
$13\div2=6 余り 1$
$6\div2=3$
$3\div2=1 余り 1$
となるので、【13】= 3です。
このとき【【2024】+7】×【33】を求めなさい。
この動画を見る
(1)
$1-0.625\div(20\dfrac{1}{24}\div20)\times(\dfrac{1}{12}-0.04)$を計算しなさい。
(2)
1から100までの100個の整数のうち、3でも7でも割り切れない偶数は何個ありますか。
(3)
【A】は整数Aを2で割り、その商を2で割っていき、商が1になるまで続けたときの2で割った数を表しています。
例えば、
$13\div2=6 余り 1$
$6\div2=3$
$3\div2=1 余り 1$
となるので、【13】= 3です。
このとき【【2024】+7】×【33】を求めなさい。
2024年渋谷教育学園渋谷中算数大問①(1)~(3)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#約数・倍数を利用する問題#過去問解説(学校別)#規則性(周期算・方陣算・数列・日暦算・N進法)#渋谷教育学園渋谷中学
指導講師:
重吉
問題文全文(内容文):
(1)
$1-0.625\div(20\dfrac{1}{24}\div20)\times(\dfrac{1}{12}-0.04)$ を計算しなさい。
(2)
1から100までの100個の整数のうち、3でも7でも割り切れない偶数は何個ありますか。
(3)
【A】は、整数Aを2で割り、その商を2で割っていき、商が1になるまで続けたときの、2で割った回数を表しています。
例えば、
13÷2=6 余り1
6÷2=3
3÷2=1 余り1
となるので、【13】=3です。
このとき、【【2024】+7】×【33】を求めなさい。
この動画を見る
(1)
$1-0.625\div(20\dfrac{1}{24}\div20)\times(\dfrac{1}{12}-0.04)$ を計算しなさい。
(2)
1から100までの100個の整数のうち、3でも7でも割り切れない偶数は何個ありますか。
(3)
【A】は、整数Aを2で割り、その商を2で割っていき、商が1になるまで続けたときの、2で割った回数を表しています。
例えば、
13÷2=6 余り1
6÷2=3
3÷2=1 余り1
となるので、【13】=3です。
このとき、【【2024】+7】×【33】を求めなさい。
【受験算数】2023年渋谷教育学園渋谷中:算数大問4解説

単元:
#算数(中学受験)#過去問解説(学校別)#渋谷教育学園渋谷中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
渋谷教育学園附属渋谷中2023年算数入試問題:大問4
式ア+イ×ウ+エ×オ×カの、アからカに異なる数を1個ずつ入れて計算した答えをAとします。
(1)1,2,3,4,5,6の6個の数をアからカに入れます。アに6、イに1をそれぞれ入れた時、Aが奇数となるAをすべて答えなさい。
(2)1,2,3,4,5,6,7,8の8個の数から6個を選んでAが奇数となるようにアからカに数を入れます。
アが偶数である時、最も大きなAと最も小さなAの差を答えなさい。
(3)1,2,3,4,5,6の6個の数をエ×オ×カが4の倍数になるようにアからカに数を入れます。
この時、Aが偶数となるAは何通りありますか?
この動画を見る
渋谷教育学園附属渋谷中2023年算数入試問題:大問4
式ア+イ×ウ+エ×オ×カの、アからカに異なる数を1個ずつ入れて計算した答えをAとします。
(1)1,2,3,4,5,6の6個の数をアからカに入れます。アに6、イに1をそれぞれ入れた時、Aが奇数となるAをすべて答えなさい。
(2)1,2,3,4,5,6,7,8の8個の数から6個を選んでAが奇数となるようにアからカに数を入れます。
アが偶数である時、最も大きなAと最も小さなAの差を答えなさい。
(3)1,2,3,4,5,6の6個の数をエ×オ×カが4の倍数になるようにアからカに数を入れます。
この時、Aが偶数となるAは何通りありますか?
2024年渋谷教育学園渋谷中算数「正多角形の角度」中学受験指導歴20年のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#渋谷教育学園渋谷中学
指導講師:
重吉
問題文全文(内容文):
動画内の図は、円と正六角形と正十角形からできています。
点Oは、円の中心です。
このとき、㋐の角の大きさは何度ですか。
出典:2024年渋谷教育学園渋谷中学高等学校 入試問題
この動画を見る
動画内の図は、円と正六角形と正十角形からできています。
点Oは、円の中心です。
このとき、㋐の角の大きさは何度ですか。
出典:2024年渋谷教育学園渋谷中学高等学校 入試問題
渋谷教育学園渋谷中学校2023年「三角形の角度」

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#渋谷教育学園渋谷中学
指導講師:
重吉
問題文全文(内容文):
渋谷教育学園渋谷中学校2023年「三角形の角度」
動画内の図を参照し、ピンクの”あ”の角度を求めよ
この動画を見る
渋谷教育学園渋谷中学校2023年「三角形の角度」
動画内の図を参照し、ピンクの”あ”の角度を求めよ
渋谷教育学園渋谷中学校2023年入試算数「計算問題」

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#渋谷教育学園渋谷中学
指導講師:
重吉
問題文全文(内容文):
渋谷教育学園渋谷中学校2023年入試算数「計算問題」
$170+99 \times (\displaystyle \frac{1}{7}-\displaystyle \frac{1}{17})\times 2023$
この動画を見る
渋谷教育学園渋谷中学校2023年入試算数「計算問題」
$170+99 \times (\displaystyle \frac{1}{7}-\displaystyle \frac{1}{17})\times 2023$
【中学受験算数】『渋渋の2022年入試の良問を丁寧に解説してみた』

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#渋谷教育学園渋谷中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
渋谷教育学園渋谷中2022入試問題大問3
(1)頂角30度、等辺の長さが5cmの二等辺三角形の面積はいくつか?
(2)1辺の長さが7cmの正三角形と、角度が45度、30度、底辺が7cmの三角形の面積の差はいくつか?(動画の図を参照)
(3)1辺9cmの正方形の内部にある、正三角形2つと正方形1つの面積の和はいくつか?(動画の図を参照)
この動画を見る
渋谷教育学園渋谷中2022入試問題大問3
(1)頂角30度、等辺の長さが5cmの二等辺三角形の面積はいくつか?
(2)1辺の長さが7cmの正三角形と、角度が45度、30度、底辺が7cmの三角形の面積の差はいくつか?(動画の図を参照)
(3)1辺9cmの正方形の内部にある、正三角形2つと正方形1つの面積の和はいくつか?(動画の図を参照)
これ解ける小学生は頭がどうかしてる!あまりにも難しすぎた1問!ノーヒントで解けたら天才だと思う【中学受験算数】【入試問題】【渋谷教育学園渋谷中学校】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#平面図形その他#渋谷教育学園渋谷中学#雙葉中学
指導講師:
こばちゃん塾
問題文全文(内容文):
2022年雙葉中学校
左図は,正方形とおうぎ形を組み合わせたものです。
正方形の面積が32㎠のとき斜線部分の面積は?
(円周率3.14)
2022渋谷教育学園渋谷中学校
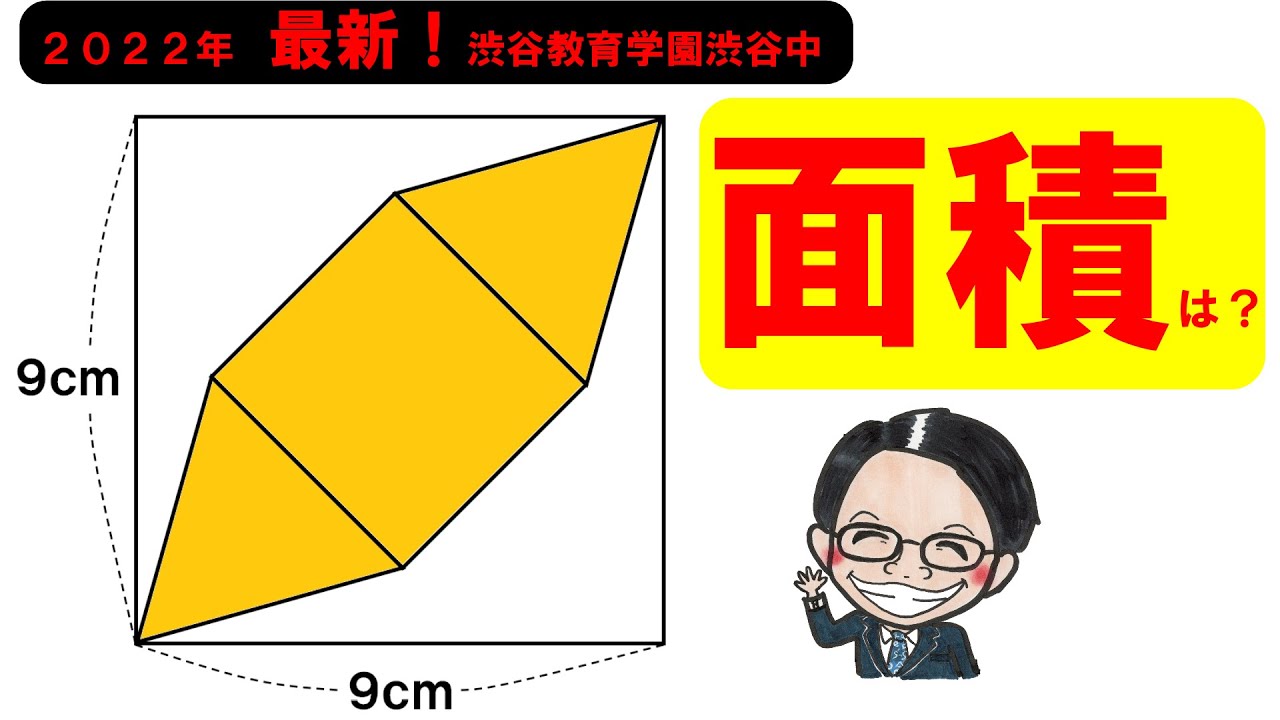
左図のように1辺の長さが9cmの正方形の中に2つの正三角形と正方形が入っています。
色がついた部分の面積は?
*図は動画内参照
この動画を見る
2022年雙葉中学校
左図は,正方形とおうぎ形を組み合わせたものです。
正方形の面積が32㎠のとき斜線部分の面積は?
(円周率3.14)
2022渋谷教育学園渋谷中学校
左図のように1辺の長さが9cmの正方形の中に2つの正三角形と正方形が入っています。
色がついた部分の面積は?
*図は動画内参照
これを解ける小学生は神すぎる!シンプルすぎる超難問!【中学受験算数】【入試問題】【渋谷教育学園渋谷中】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#平面図形その他#渋谷教育学園渋谷中学
指導講師:
こばちゃん塾
問題文全文(内容文):
2022渋谷教育学園渋谷中学校
A~Ⅰにはそれぞれ0~9の数字が1つずつ入る。
Cが6、HがO、A~Iで使わなかった数字をPとする。
ABCが考えられる数の中で最大となるとき,BとPの数は?
2022渋谷教育学園渋谷中学校
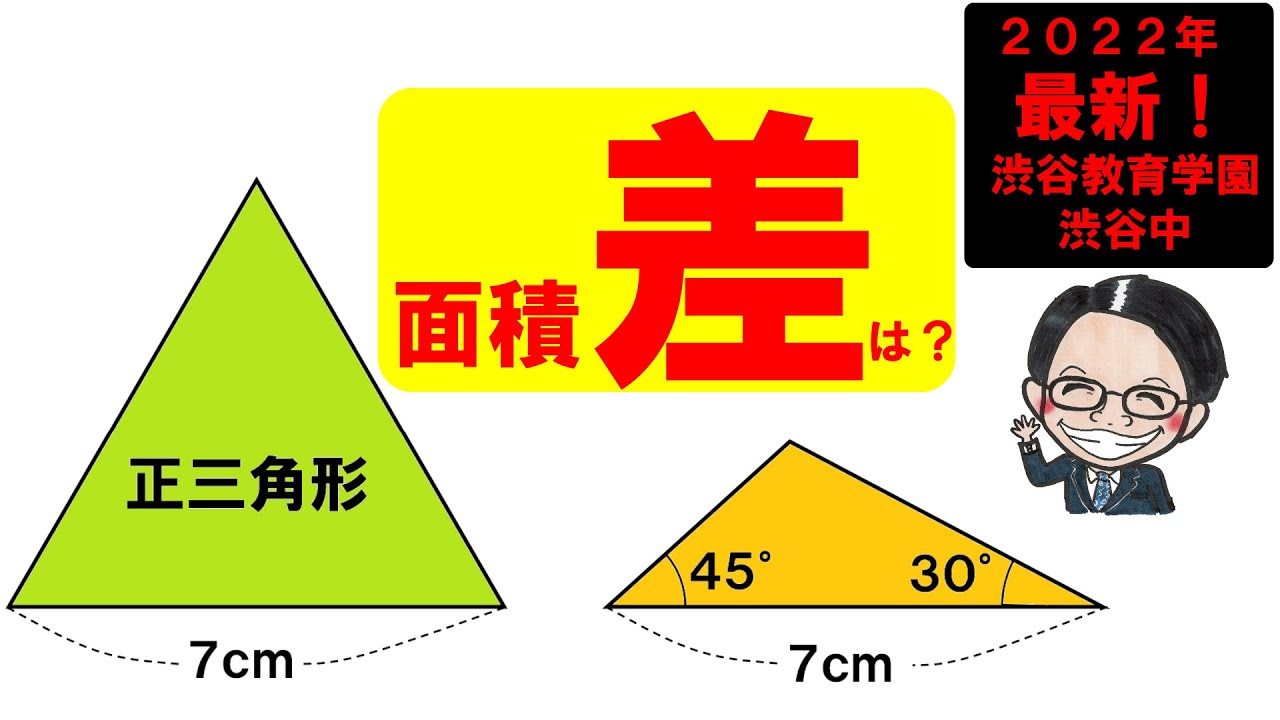
1辺の長さが7cmの正三角形の面積と,図1の三角形の面積の差は何㎤ですか?
図2を利用して求めましょう
*図は動画内参照
この動画を見る
2022渋谷教育学園渋谷中学校
A~Ⅰにはそれぞれ0~9の数字が1つずつ入る。
Cが6、HがO、A~Iで使わなかった数字をPとする。
ABCが考えられる数の中で最大となるとき,BとPの数は?
2022渋谷教育学園渋谷中学校
1辺の長さが7cmの正三角形の面積と,図1の三角形の面積の差は何㎤ですか?
図2を利用して求めましょう
*図は動画内参照
【最強裏技あります!】この1問を徹底解説!通常の解き方から裏技の成り立ちまで丁寧に解説!【中学受験算数】【入試問題】【渋谷教育学園渋谷中】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#渋谷教育学園渋谷中学
指導講師:
こばちゃん塾
問題文全文(内容文):
2021渋谷教育学園渋谷中学校
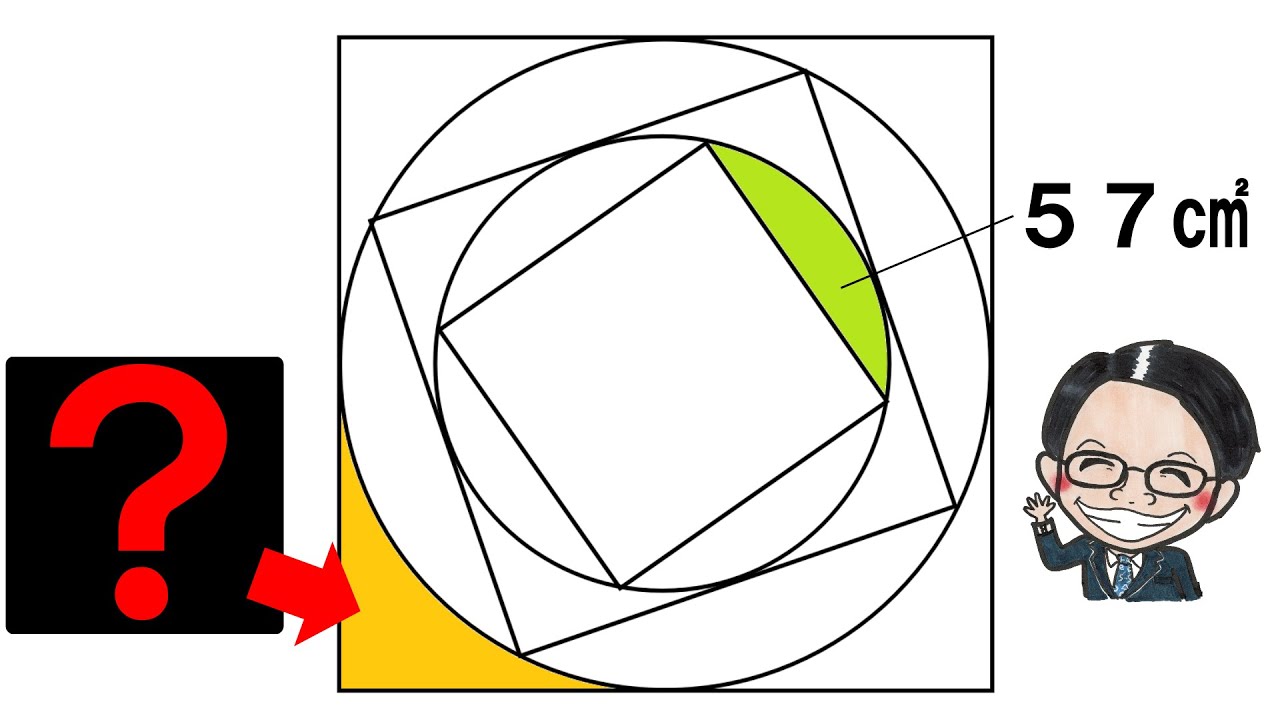
下図は正方形と円でできている。
㋐が57㎠のとき、㋑は何㎠?
*図は動画内参照
この動画を見る
2021渋谷教育学園渋谷中学校
下図は正方形と円でできている。
㋐が57㎠のとき、㋑は何㎠?
*図は動画内参照
【第17問】渋谷教育学園渋谷中学2017年の入試問題【気付けばスッキリ!受験算数】
単元:
#算数(中学受験)#過去問解説(学校別)#渋谷教育学園渋谷中学
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
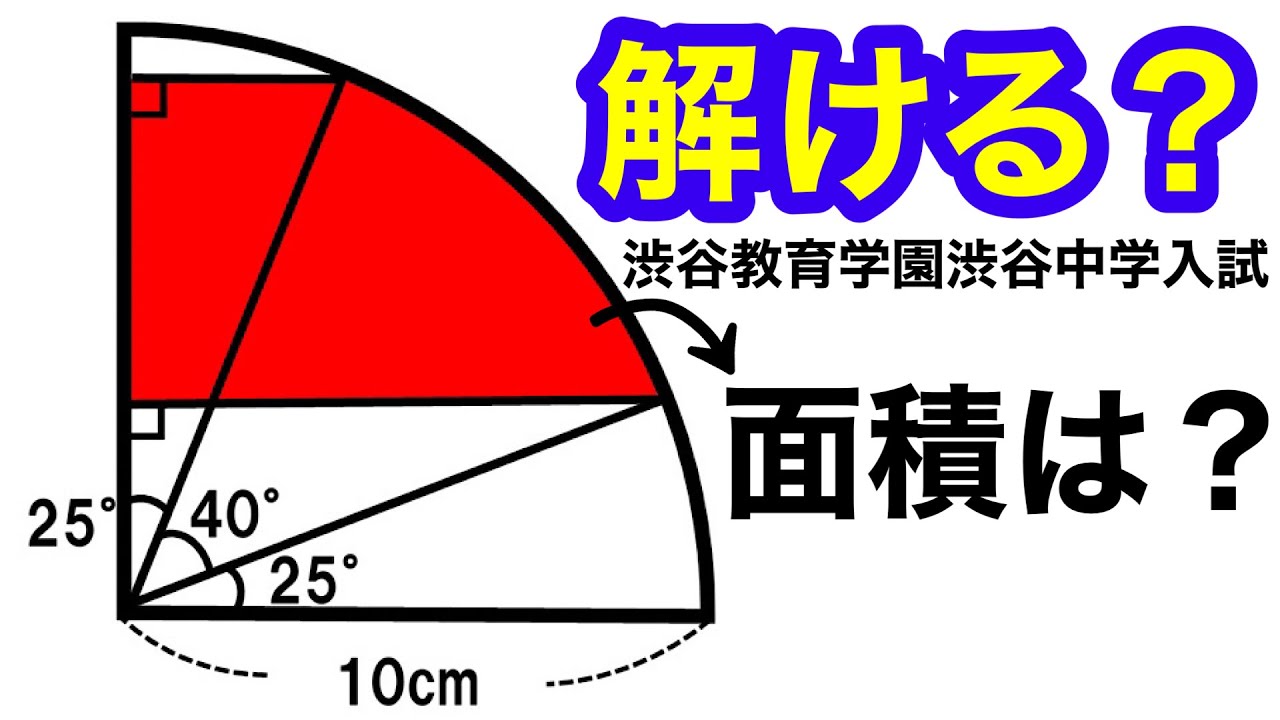
第17問を解説します。
渋谷教育学園渋谷中学2017年の入試問題
この動画を見る
第17問を解説します。
渋谷教育学園渋谷中学2017年の入試問題
