 場合の数
場合の数
 場合の数
場合の数
【小6算数手元解説】サイコロを何回か投げて出た目の和が7になった【問題文は概要欄】

単元:
#算数(中学受験)#場合の数#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
1個のサイコロを2回以上何回か投げて、出た目を加えたら7になりました。
1) サイコロの投げた回数は最高で何回と考えられますか。
2) 目の出方は全部で何通りありますか。ただし、目の出方を数えるときは、例えば、投げた順に2,1,1と出るのと、1,2,1と出るのとは、ちがう出方と考えます。
この動画を見る
1個のサイコロを2回以上何回か投げて、出た目を加えたら7になりました。
1) サイコロの投げた回数は最高で何回と考えられますか。
2) 目の出方は全部で何通りありますか。ただし、目の出方を数えるときは、例えば、投げた順に2,1,1と出るのと、1,2,1と出るのとは、ちがう出方と考えます。
福田のおもしろ数学159〜俳句はスパコンとAIで終了してしまうのか

福田のおもしろ数学101〜円の中の領域の塗り分け
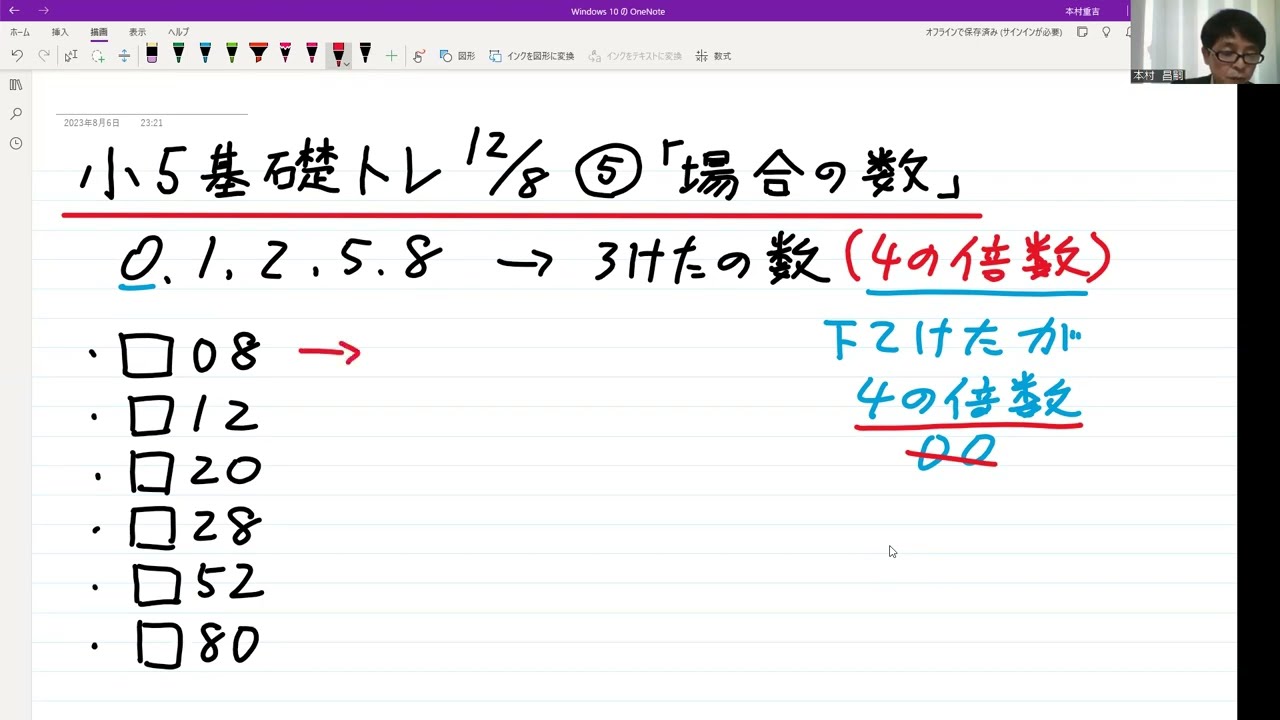
小5基礎トレ算数解説12/8⑤「場合の数」
単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#中学受験教材#小5基礎訓練
指導講師:
重吉
問題文全文(内容文):
【場合の数】
0,1,2,5,8のカードがあります。
この中から3枚のカードを選び、3桁の数を作ります
3桁の数で4の倍数になる並びは何通りありますか?
この動画を見る
【場合の数】
0,1,2,5,8のカードがあります。
この中から3枚のカードを選び、3桁の数を作ります
3桁の数で4の倍数になる並びは何通りありますか?
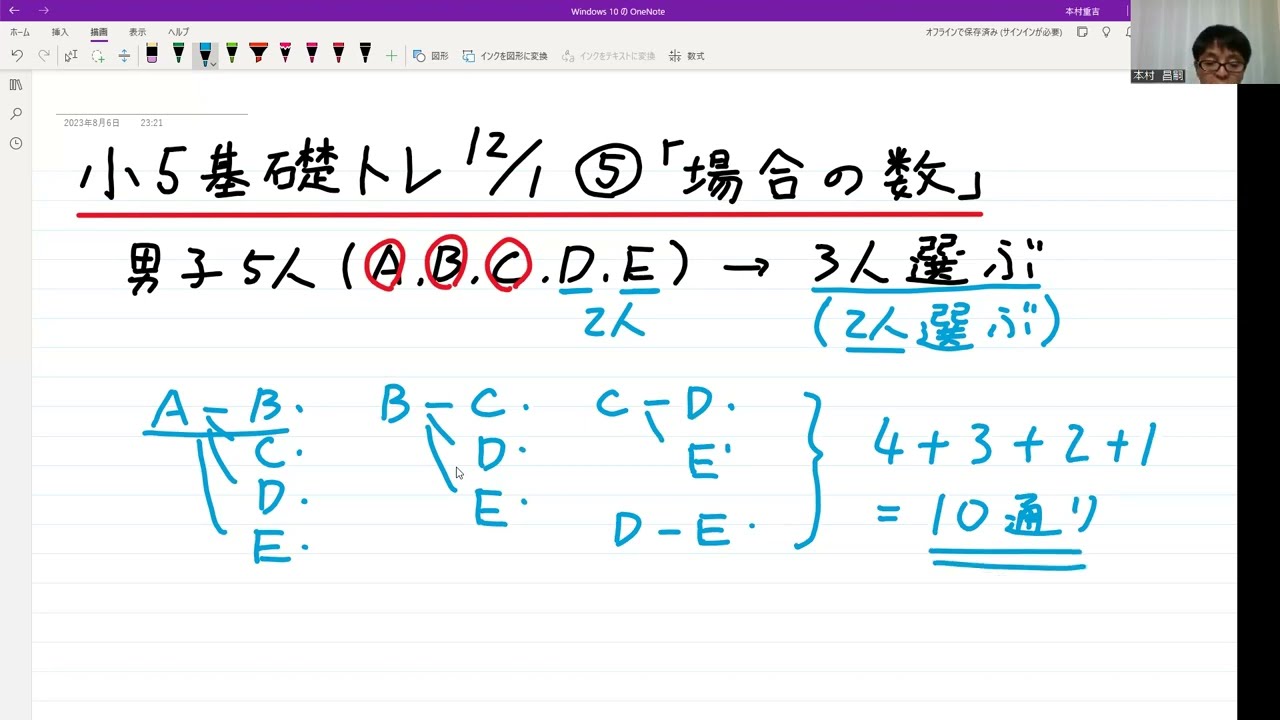
小5基礎トレ算数解説12/1⑤「場合の数」
単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#中学受験教材#小5基礎訓練
指導講師:
重吉
問題文全文(内容文):
【場合の数】
男子5人と女子の4人の中からバスケットボール選手を選びます。
男子3名、女子2人を選ぶときの組み合わせの場合の数を求めよ
この動画を見る
【場合の数】
男子5人と女子の4人の中からバスケットボール選手を選びます。
男子3名、女子2人を選ぶときの組み合わせの場合の数を求めよ
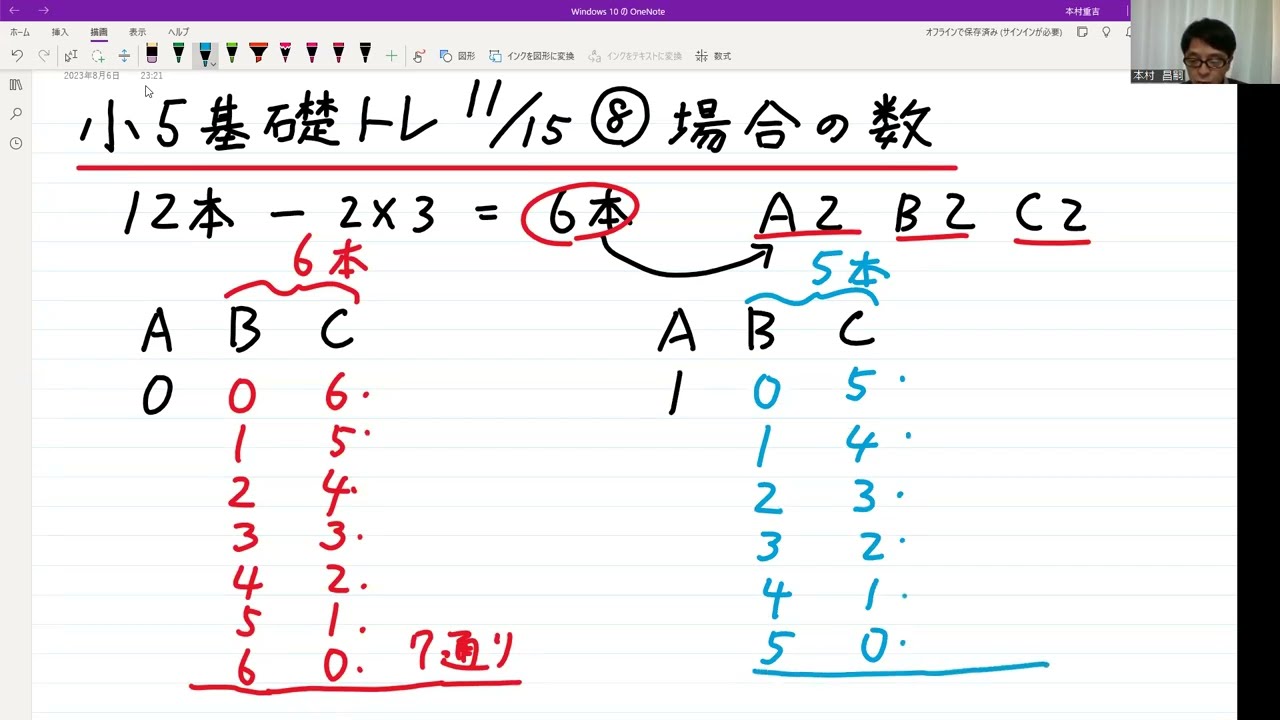
小5基礎トレ算数解説11/15⑧「場合の数」
単元:
#算数(中学受験)#場合の数#場合の数
指導講師:
重吉
問題文全文(内容文):
【場合の数】
12本の鉛筆をA,B,Cに分けます。
3人とも少なくとも2本ずつは受け取ります
残りの鉛筆を配るのに何通り分け方があるか求めよ。
この動画を見る
【場合の数】
12本の鉛筆をA,B,Cに分けます。
3人とも少なくとも2本ずつは受け取ります
残りの鉛筆を配るのに何通り分け方があるか求めよ。
2023年中央大学附属中学校算数「場合の数(道順)」

単元:
#算数(中学受験)#過去問解説(学校別)#場合の数#場合の数#中央大学附属中学
指導講師:
重吉
問題文全文(内容文):
2023年中央大学附属中学校算数「場合の数(道順)」
A地点からB地点を遠回りせず、✕地点を通らない場合、行き方の場合の数を求めよ。
この動画を見る
2023年中央大学附属中学校算数「場合の数(道順)」
A地点からB地点を遠回りせず、✕地点を通らない場合、行き方の場合の数を求めよ。
2023年灘中学校入試問題「場合の数」

単元:
#算数(中学受験)#過去問解説(学校別)#場合の数#場合の数#灘中学校
指導講師:
重吉
問題文全文(内容文):
2023年灘中学校入試問題「場合の数」
※動画内の図参照
(1)三角形ができない3点の選び方は何通りあるか求めよ
(2)三角形ができる選び方は何通りあるか求めよ
この動画を見る
2023年灘中学校入試問題「場合の数」
※動画内の図参照
(1)三角形ができない3点の選び方は何通りあるか求めよ
(2)三角形ができる選び方は何通りあるか求めよ
【受験算数】さいころを3回振ったところ、1回目よりも2回目の方が大きい目が出て、さらに2回目よりも3回目の方が大きい目が出ました。このような目の出方は□通りです。

単元:
#算数(中学受験)#場合の数#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
さいころを3回振ったところ、1回目よりも2回目の方が大きい目が出て、さらに2回目よりも3回目の方が大きい目が出ました。このような目の出方は□通りです。
この動画を見る
さいころを3回振ったところ、1回目よりも2回目の方が大きい目が出て、さらに2回目よりも3回目の方が大きい目が出ました。このような目の出方は□通りです。
予習シリーズ算数6年上P93「ステップアップ演習」⑤

単元:
#算数(中学受験)#場合の数#場合の数
指導講師:
重吉
問題文全文(内容文):
10個のボールをABCDの4つの箱に入れる個数の分け方、場合の数は何通りあるか求めよ
(別解)
和が10になる4つの整数の組み合わせでそれぞれ何通りあるか求めよ
①3個が同じ数字、1個が異なる数字
②2個ずつ同じ数字が2組
③2個同じ数字1組と異なる2個の数字
④4個の数字がすべて異なる数字
この動画を見る
10個のボールをABCDの4つの箱に入れる個数の分け方、場合の数は何通りあるか求めよ
(別解)
和が10になる4つの整数の組み合わせでそれぞれ何通りあるか求めよ
①3個が同じ数字、1個が異なる数字
②2個ずつ同じ数字が2組
③2個同じ数字1組と異なる2個の数字
④4個の数字がすべて異なる数字
【受験算数】『聖光の2022年入試問題【場合の数】を丁寧に解いてみた』

単元:
#算数(中学受験)#過去問解説(学校別)#場合の数#場合の数#聖光学院中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
1~5までの数字が書かれた赤・白・青の3色の玉が1個ずつ合計15個あります。
(1)15個の玉の中から5個の玉を選んで一列に並べる並べ方のうち、左から順に赤・赤・白・白・白と並ぶような玉の並べ方は全部で何通りありますか?
(2)15個の玉の中から3個の玉を選んで一列に並べます。玉に書かれた数字を左から百の位・十の位・一の位として3桁の数字を作る時、
【ア】3桁の数字が144となるような玉の並べ方は全部で何通りありますか?
【イ】3桁の数字が18の倍数となるような玉の並べ方は全部で何通りありますか?
(3)15個の玉の中から4個の玉を選んで一列に並べ、玉に書かれた数字を左から千の位・百の位・十の位・一の位として4桁の数を作ることを考えます。今、ある4個の玉を選んだところ、それぞれの並べ方から作られる数の総和は106656となりました。玉に書かれている4つの数字の組み合わせとして考えられるものを全て答えなさい。
この動画を見る
1~5までの数字が書かれた赤・白・青の3色の玉が1個ずつ合計15個あります。
(1)15個の玉の中から5個の玉を選んで一列に並べる並べ方のうち、左から順に赤・赤・白・白・白と並ぶような玉の並べ方は全部で何通りありますか?
(2)15個の玉の中から3個の玉を選んで一列に並べます。玉に書かれた数字を左から百の位・十の位・一の位として3桁の数字を作る時、
【ア】3桁の数字が144となるような玉の並べ方は全部で何通りありますか?
【イ】3桁の数字が18の倍数となるような玉の並べ方は全部で何通りありますか?
(3)15個の玉の中から4個の玉を選んで一列に並べ、玉に書かれた数字を左から千の位・百の位・十の位・一の位として4桁の数を作ることを考えます。今、ある4個の玉を選んだところ、それぞれの並べ方から作られる数の総和は106656となりました。玉に書かれている4つの数字の組み合わせとして考えられるものを全て答えなさい。
久留米大学附設中学校2023年入試「場合の数」

単元:
#算数(中学受験)#過去問解説(学校別)#場合の数#場合の数#久留米大学附設中学
指導講師:
重吉
問題文全文(内容文):
久留米大学附設中学校2023年入試「場合の数」
(1)ア+イ+ウ=6のとき、何通りあるか求めよ
(2)ア+イ+ウ=12のとき、何通りあるか求めよ
(3)ア+イ+ウ=18のとき、何通りあるか求めよ
この動画を見る
久留米大学附設中学校2023年入試「場合の数」
(1)ア+イ+ウ=6のとき、何通りあるか求めよ
(2)ア+イ+ウ=12のとき、何通りあるか求めよ
(3)ア+イ+ウ=18のとき、何通りあるか求めよ
フェリス女学院中学校2023年「場合の数」

単元:
#算数(中学受験)#過去問解説(学校別)#場合の数#場合の数#フェリス女学院中学
指導講師:
重吉
問題文全文(内容文):
フェリス女学院中学校2023年「場合の数」
(1)サイコロを3回振って、その出た目のかけ算の答えが偶数となる場合は何通りあるか求めよ
(2)8の倍数になる場合は何通りあるか求めよ
この動画を見る
フェリス女学院中学校2023年「場合の数」
(1)サイコロを3回振って、その出た目のかけ算の答えが偶数となる場合は何通りあるか求めよ
(2)8の倍数になる場合は何通りあるか求めよ
武蔵中学校2023年算数「場合の数」

単元:
#算数(中学受験)#過去問解説(学校別)#場合の数#場合の数#武蔵中学
指導講師:
重吉
問題文全文(内容文):
武蔵中学校2023年算数「場合の数」
(1)6人中、田中さんが3人、木村さんが3人いて、それぞれはばらばらの部屋に入ります。
このとき部屋割りは何通りあるか求めよ
(2)6人中、田中さんが2人、木村さんが2人、川野さんが2人いて、各部屋に2人ずつ入る止まり方は何通りあるか求めよ
また、3組の兄弟が同部屋の組み合わせは何通りか、1組の兄弟が同部屋の組み合わせは何通りか
この動画を見る
武蔵中学校2023年算数「場合の数」
(1)6人中、田中さんが3人、木村さんが3人いて、それぞれはばらばらの部屋に入ります。
このとき部屋割りは何通りあるか求めよ
(2)6人中、田中さんが2人、木村さんが2人、川野さんが2人いて、各部屋に2人ずつ入る止まり方は何通りあるか求めよ
また、3組の兄弟が同部屋の組み合わせは何通りか、1組の兄弟が同部屋の組み合わせは何通りか
中学生の解き方 高校生の解き方

単元:
#算数(中学受験)#数A#場合の数と確率#場合の数#場合の数#場合の数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
区別のつかない5個のボールがある。これらすべてをA,B,Cの3人に配るとき何通りあるか?
(ただし1個ももらえない人はいない)
西南学院高等学校
この動画を見る
区別のつかない5個のボールがある。これらすべてをA,B,Cの3人に配るとき何通りあるか?
(ただし1個ももらえない人はいない)
西南学院高等学校
【受験算数】樹形図より簡単!4枚のカードから偶数を作る【受験算数】場合の数:樹形図より簡単!4枚のカードから偶数を作る【予習シリーズ算数・小5上】

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
{0,1,2,3}の4枚のカードがあります。このうち3枚を並べて3けたの整数を作ります。偶数は何通りできますか。
この動画を見る
{0,1,2,3}の4枚のカードがあります。このうち3枚を並べて3けたの整数を作ります。偶数は何通りできますか。
【受験算数】樹形図より簡単!0がある場合のカードの並べ方【予習シリーズ算数・小5上】

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
{0,1,2,3}の4枚のカードがあります。このうち3枚を並べて3けたの整数を作ります。整数は何通りできますか。
この動画を見る
{0,1,2,3}の4枚のカードがあります。このうち3枚を並べて3けたの整数を作ります。整数は何通りできますか。
【受験算数】場合の数:樹形図より簡単!4枚のカードから2桁の整数を作る場合の数【予習シリーズ算数・小5上】

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
{1,2,3,4}の4枚のカードがあります。このうちの2枚を並べて2けたの整数を作ります。整数は何通りできますか。
この動画を見る
{1,2,3,4}の4枚のカードがあります。このうちの2枚を並べて2けたの整数を作ります。整数は何通りできますか。
【受験算数】場合の数:ぬり分けの問題~全色使う場合!【予習シリーズ算数・小5上】

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
{赤,青,黄,緑}のうちの何色かを使って、右の図のア~エの4つの部分を、となり合う部分が同じ色にならないようにぬり分けます。4色全部を使うとき、色のぬり方は何通りありますか。
この動画を見る
{赤,青,黄,緑}のうちの何色かを使って、右の図のア~エの4つの部分を、となり合う部分が同じ色にならないようにぬり分けます。4色全部を使うとき、色のぬり方は何通りありますか。
【受験算数】場合の数:ぬり分けの問題~4色から3色選んでぬり分けるなら何通り?【予習シリーズ算数・小5上】

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
{赤,青,黄,緑}のうちの何色かを使って、右の図のア~エの4つの部分を、となり合う部分が同じ色にならないようにぬり分けます。3色ちょうどを使うとき、色のぬり方は何通りありますか。
この動画を見る
{赤,青,黄,緑}のうちの何色かを使って、右の図のア~エの4つの部分を、となり合う部分が同じ色にならないようにぬり分けます。3色ちょうどを使うとき、色のぬり方は何通りありますか。
【受験算数】場合の数:道順の場合の数通るべき点がある場合~イチイチ解法【予習シリーズ算数・小5上】

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のような、直角に交わる道があります。点Aから点Cを通って点Bまで行くとき、遠回りせずに行く道順は何通りありますか。
この動画を見る
図のような、直角に交わる道があります。点Aから点Cを通って点Bまで行くとき、遠回りせずに行く道順は何通りありますか。
【受験算数】場合の数:道順の場合の数 通ってはいけない場所がある場合~イチイチ解法【予習シリーズ算数・小5上】

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のような、直角に交わる道があります。点Aから点Cを通って点Bまで行くとき、遠回りせずに行く道順は何通りありますか。
この動画を見る
図のような、直角に交わる道があります。点Aから点Cを通って点Bまで行くとき、遠回りせずに行く道順は何通りありますか。
【受験算数】場合の数:道順の場合の数~イチイチ解法【予習シリーズ算数・小5上】
単元:
#算数(中学受験)#場合の数#場合の数
教材:
#予習シ#予習シ算数・小5上#中学受験教材#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
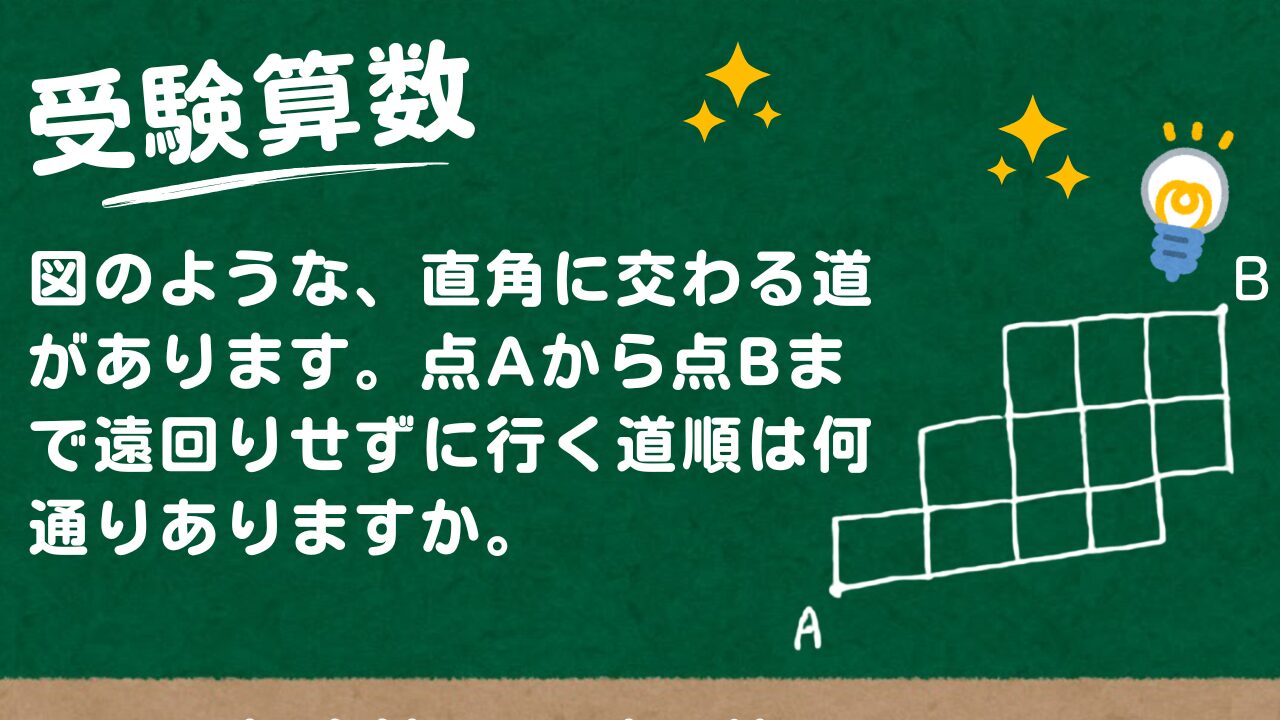
図のような、直角に交わる道があります。点Aから点Bまで遠回りせずに行く道順は何通りありますか。
この動画を見る
図のような、直角に交わる道があります。点Aから点Bまで遠回りせずに行く道順は何通りありますか。
解けるかな?

単元:
#算数(中学受験)#数A#場合の数と確率#場合の数#場合の数#場合の数#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
机の上にたくさんのコインが置いてます。
そのうち10枚だけ表、残りは全部裏が上になっています。
目隠しをした状態で表が上になっているコインの枚数が同じような
2つのグループに分けるにはどうすればよいか?
ただし、触って表裏の判断はできないとする
この動画を見る
机の上にたくさんのコインが置いてます。
そのうち10枚だけ表、残りは全部裏が上になっています。
目隠しをした状態で表が上になっているコインの枚数が同じような
2つのグループに分けるにはどうすればよいか?
ただし、触って表裏の判断はできないとする
【受験算数】早稲田中2007年:図形の問題と思いきや場合の数!

単元:
#算数(中学受験)#過去問解説(学校別)#場合の数#場合の数#早稲田中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
2007年早稲田中学大問2(2)の問題です。
下の図2のように、高さが6㎝の正三角形の内部の点Pから辺BC、CA、ABへ垂線を引き、その長さをそれぞれxcm、ycm、zcmとします。
x、y、zがすべて整数であるような点Pは全部で何個ありますか。
この動画を見る
2007年早稲田中学大問2(2)の問題です。
下の図2のように、高さが6㎝の正三角形の内部の点Pから辺BC、CA、ABへ垂線を引き、その長さをそれぞれxcm、ycm、zcmとします。
x、y、zがすべて整数であるような点Pは全部で何個ありますか。
【第36問】大宮開成中学2020年の入試問題【気付けばスッキリ!受験算数】
単元:
#算数(中学受験)#過去問解説(学校別)#場合の数#場合の数#大宮開成中学
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
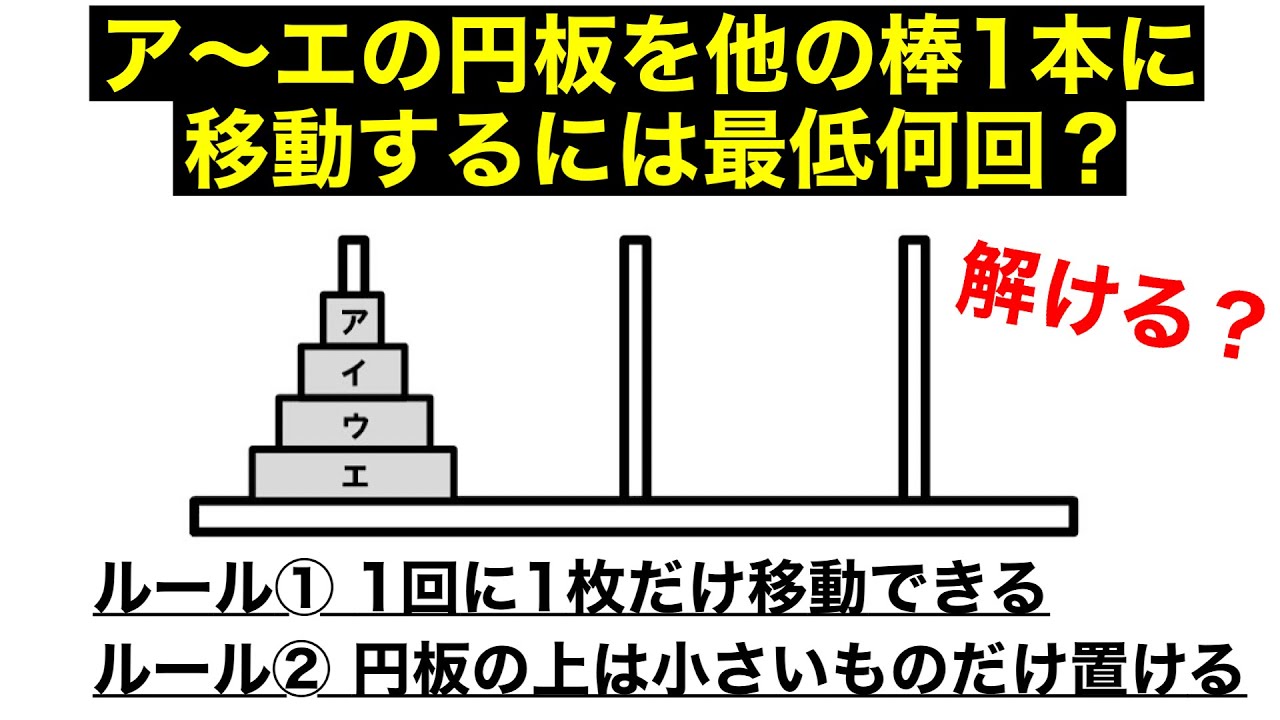
ア~エの円板を他の棒1本にすべて移動させるには、最低何回移動するか。
~ルール~
・1回の移動は1枚だけ
・円板の上には、小さいものだけ置くことができる。
*図は動画内参照
2020大宮開成中学入試過去問
この動画を見る
ア~エの円板を他の棒1本にすべて移動させるには、最低何回移動するか。
~ルール~
・1回の移動は1枚だけ
・円板の上には、小さいものだけ置くことができる。
*図は動画内参照
2020大宮開成中学入試過去問
【受験算数】場合の数:全16チームでトーナメント戦を行うとき、全部で何試合行うことになるか求めよ。

【中学数学・数A】中高一貫校問題集3(論理・確率編)61:場合の数と確率:場合の数:硬貨の選び方 5円玉4枚、10円玉2枚、50円玉1枚、100円玉2枚の一部、または全部使って支払うことができる金額は何通りか求めよう。

単元:
#算数(中学受験)#数A#場合の数と確率#場合の数#場合の数#場合の数#数学(高校生)
教材:
#TK数学#TK数学問題集3(論理・確率編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
5円玉4枚、10円玉2枚、50円玉1枚、100円玉2枚の一部、または全部使って支払うことができる金額は何通りか求めよう。
この動画を見る
5円玉4枚、10円玉2枚、50円玉1枚、100円玉2枚の一部、または全部使って支払うことができる金額は何通りか求めよう。
【受験算数】場合の数:不定方程式! Aは1個35円、Bは1個45円です。律子は1260円の所持金をちょうど全部使って2種類とも買うつもりです。A,Bをそれぞれ何個ずつ買うことができますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
A,Bの2種類の品物があります。Aは1個35円、Bは1個45円です。律子は1260円の所持金をちょうど全部使って、2種類とも買うつもりです。A,Bをそれぞれ何個ずつ買うことができますか。すべての場合を答えなさい。
この動画を見る
A,Bの2種類の品物があります。Aは1個35円、Bは1個45円です。律子は1260円の所持金をちょうど全部使って、2種類とも買うつもりです。A,Bをそれぞれ何個ずつ買うことができますか。すべての場合を答えなさい。
【受験算数】場合の数:三角形を作る! 右の図のように2本の直線の上に8個の点があります。そのうち3点を頂点とする三角形は何通りありますか。

単元:
#算数(中学受験)#場合の数#場合の数
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のように2本の直線の上に8個の点があります。そのうち3点を頂点とする三角形は何通りありますか。
この動画を見る
右の図のように2本の直線の上に8個の点があります。そのうち3点を頂点とする三角形は何通りありますか。
