 算数(中学受験)
算数(中学受験)
 算数(中学受験)
算数(中学受験)
【中学受験算数】【ともなって変わる2つの量】ゼロから始める中学受験算数25 ややこしいを簡単!に変える!ともなって変わる2つの量!!

単元:
#算数(中学受験)#文章題#文章題その他
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣0.6mで240円のリボンがあります。このリボン3.5mのねだんは何円ですか。
2⃣0.8mの重さが20gの針金があります。この針金5mの重さは何gですか。
3⃣アメリカの通過である1ドルが105円、中国の通貨である1元が15円であるとき、630元は何ドルですか。
4⃣アメリカの通過である1ドルが105円、イギリスの通過である1ポンドが165円であるとき、770ポンドは何ドルですか。
5⃣歯数24の歯車Aと歯数16の歯車Bがかみ合っています。
Aを12回転させると、Bは何回転しますか。
6⃣歯数32の歯車Aと歯数48の歯車Bがかみ合っています。
Aを60回転させると、Bは何回転しますか。
7⃣あるバネに50gのおもりをつるすとバネの長さは20㎝になり、75gのおもりをつるすとバネの長さは25㎝になります。もとのバネの長さは何㎝ですか。
この動画を見る
1⃣0.6mで240円のリボンがあります。このリボン3.5mのねだんは何円ですか。
2⃣0.8mの重さが20gの針金があります。この針金5mの重さは何gですか。
3⃣アメリカの通過である1ドルが105円、中国の通貨である1元が15円であるとき、630元は何ドルですか。
4⃣アメリカの通過である1ドルが105円、イギリスの通過である1ポンドが165円であるとき、770ポンドは何ドルですか。
5⃣歯数24の歯車Aと歯数16の歯車Bがかみ合っています。
Aを12回転させると、Bは何回転しますか。
6⃣歯数32の歯車Aと歯数48の歯車Bがかみ合っています。
Aを60回転させると、Bは何回転しますか。
7⃣あるバネに50gのおもりをつるすとバネの長さは20㎝になり、75gのおもりをつるすとバネの長さは25㎝になります。もとのバネの長さは何㎝ですか。
【受験算数】変化のグラフ: 中じきりのある水そうの左側から毎分一定量の割合で水を入れます。しきりの高さyは何cmですか。

単元:
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のような中じきりのある水そうの左側から毎分一定量の割合で水を入れます。
(2)しきりの高さyは何cmですか。
この動画を見る
右の図のような中じきりのある水そうの左側から毎分一定量の割合で水を入れます。
(2)しきりの高さyは何cmですか。
【中学受験算数】【ニュートン算】【仕事算】ゼロから始める中学受験算数24 最難関をズバッと解決!仕事算・ニュートン算!!

単元:
#算数(中学受験)#文章題#仕事算とニュートン算
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣ある仕事をA1人ですると15日、B1人ですると10日かかります。この仕事をA,B2人でやると、何日かかりますか。
2⃣ある仕事をA1人ですると20分、B1人ですると30分かかります。この仕事をA,B2人でやると、何分かかりますか。
3⃣8人で働いて15日で仕上がる仕事を、はじめの7日間は10人で働き、そのあとは5人で働きました。この仕事を終えるのに、全部で何日かかりましたか。
4⃣6人で働いて15日で仕上がる仕事を、はじめの6日間は5人で働き、そのあとは4人で働きました。この仕事を終えるのに、全部で何日かかりましたか。
5⃣動物園の開園前に300人の行列ができていて、開園後も毎分15人ずつ行列に加わります。開園後、ゲートを1つだけ開けると、行列は10分でなくなります。ゲートを3つ開けると、行列は何分何秒でなくなる?
6⃣映画館の開館前に160人の行列ができていて、開館後も毎分10人ずつ行列に加わります。開館後、ゲートを1つだけ開けると、行列は8分でなくなります。ゲートを2つ開けると、行列は何分何秒でなくなる?
この動画を見る
1⃣ある仕事をA1人ですると15日、B1人ですると10日かかります。この仕事をA,B2人でやると、何日かかりますか。
2⃣ある仕事をA1人ですると20分、B1人ですると30分かかります。この仕事をA,B2人でやると、何分かかりますか。
3⃣8人で働いて15日で仕上がる仕事を、はじめの7日間は10人で働き、そのあとは5人で働きました。この仕事を終えるのに、全部で何日かかりましたか。
4⃣6人で働いて15日で仕上がる仕事を、はじめの6日間は5人で働き、そのあとは4人で働きました。この仕事を終えるのに、全部で何日かかりましたか。
5⃣動物園の開園前に300人の行列ができていて、開園後も毎分15人ずつ行列に加わります。開園後、ゲートを1つだけ開けると、行列は10分でなくなります。ゲートを3つ開けると、行列は何分何秒でなくなる?
6⃣映画館の開館前に160人の行列ができていて、開館後も毎分10人ずつ行列に加わります。開館後、ゲートを1つだけ開けると、行列は8分でなくなります。ゲートを2つ開けると、行列は何分何秒でなくなる?
【中学受験算数】【倍数算】ゼロから始める中学受験算数23 難問をあっさり攻略!倍数算・年齢算はこう解け!!【年齢算】

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣
(1)はじめ、姉と妹の所持金の比は3:2でしたが、姉が妹に60円あげたので、2人の所持金の比は5:4になりました。はじめの姉の所持金は何円?
(2)はじめ、兄と弟が持っているカードの枚数の比は3:1でしたが、兄が弟に6枚あげたので、2人の枚数の比は2:1になりました。はじめ兄は何枚持っていた?
(3)はじめ兄と弟の所持金の比は5:3でしたが、2人とも500円ずつ使ったので、2人の所持金の比は9:5になりました。はじめの兄の所持金は何円でしたか。
(4)はじめ、姉と妹の持っている折り紙の枚数の比は8:5でしたが、2人とも22枚ずつ使ったので、2人の枚数の比は7:3になりました。はじめ妹は何枚持っていましたか。
2⃣現在、母は33才、子供は7才です。母の年れいが子供の年れいの3倍になるのは、今から何年後ですか。
3⃣現在父は40才で、子供は12才です。父の年れいが子供の年れいの2倍になるのは、今から何年後ですか。
この動画を見る
1⃣
(1)はじめ、姉と妹の所持金の比は3:2でしたが、姉が妹に60円あげたので、2人の所持金の比は5:4になりました。はじめの姉の所持金は何円?
(2)はじめ、兄と弟が持っているカードの枚数の比は3:1でしたが、兄が弟に6枚あげたので、2人の枚数の比は2:1になりました。はじめ兄は何枚持っていた?
(3)はじめ兄と弟の所持金の比は5:3でしたが、2人とも500円ずつ使ったので、2人の所持金の比は9:5になりました。はじめの兄の所持金は何円でしたか。
(4)はじめ、姉と妹の持っている折り紙の枚数の比は8:5でしたが、2人とも22枚ずつ使ったので、2人の枚数の比は7:3になりました。はじめ妹は何枚持っていましたか。
2⃣現在、母は33才、子供は7才です。母の年れいが子供の年れいの3倍になるのは、今から何年後ですか。
3⃣現在父は40才で、子供は12才です。父の年れいが子供の年れいの2倍になるのは、今から何年後ですか。
【受験算数 】旅人算:甲は右の図のような交差点の南方3900mの地点から北へ、乙は交差点から東へ同時に歩き始めました。15分後に2人の位置は交差点から等距離になり、その50分後にも交差点から等距離になりました。甲と乙の分速はそれぞれ何mですか。

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
甲は右の図のような交差点の南方3900mの地点から北へ、乙は交差点から東へ同時に歩き始めました。15分後に2人の位置は交差点から等距離になり、その50分後にも交差点から等距離になりました。甲と乙の分速はそれぞれ何mですか。
この動画を見る
甲は右の図のような交差点の南方3900mの地点から北へ、乙は交差点から東へ同時に歩き始めました。15分後に2人の位置は交差点から等距離になり、その50分後にも交差点から等距離になりました。甲と乙の分速はそれぞれ何mですか。
【中学受験算数】【比の性質】ゼロから始める中学受験算数22 学校で習わない方法で簡単に解く!比の性質!!

単元:
#算数(中学受験)#単位・比と割合・比例・反比例
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣次の比を簡単にしましょう。
(1)12:9
(2)0.6:1.4
(3)$\frac{1}{2}:\frac{2}{3}$
(4)98:70
(5)3.5:2.8
(6)$\frac{4}{5}:\frac{1}{6}$
(7)$2\frac{2}{3}:1\frac{5}{6}$
2⃣次の式の▢にあてはまる数を求めましょう。
(1)▢:7=12:21
(2)42:35=▢:10
(3)▢:18=28:63
(4)$\frac{2}{3}:\frac{1}{2}=▢:9$
3⃣112枚のカードを兄と弟の2人で分けます。兄と弟の枚数の比を4:3にするとき、2人の枚数をそれぞれ求めましょう。
4⃣60個のあめを姉と弟の2人で分けます。姉と弟の個数の比を3:2にするとき、2人の個数をそれぞれ求めましょう。
この動画を見る
1⃣次の比を簡単にしましょう。
(1)12:9
(2)0.6:1.4
(3)$\frac{1}{2}:\frac{2}{3}$
(4)98:70
(5)3.5:2.8
(6)$\frac{4}{5}:\frac{1}{6}$
(7)$2\frac{2}{3}:1\frac{5}{6}$
2⃣次の式の▢にあてはまる数を求めましょう。
(1)▢:7=12:21
(2)42:35=▢:10
(3)▢:18=28:63
(4)$\frac{2}{3}:\frac{1}{2}=▢:9$
3⃣112枚のカードを兄と弟の2人で分けます。兄と弟の枚数の比を4:3にするとき、2人の枚数をそれぞれ求めましょう。
4⃣60個のあめを姉と弟の2人で分けます。姉と弟の個数の比を3:2にするとき、2人の個数をそれぞれ求めましょう。
【中学受験算数】【相当算】ゼロから始める中学受験算数21 難問もスッキリ解決!相当算の簡単な解き方!!

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣コップの中のジュースを60%飲んだら、残りは80mLになりました。はじめ、コップの中には、何mLのジュースが入っていましたか。
2⃣所持金の70%を使って本を買ったら、残金は450円になりました。はじめの所持金は何円でしたか。
3⃣ある本を、1日目は全体の$\frac{3}{7}$を読み、2日目は残りの$\frac{5}{6}$を読んだので、残りは24ページありますか。
4⃣ある本を、1日目は全体の$\frac{1}{4}$を読み、2日目は残りの$\frac{2}{3}$を読んだので、残りは60ページになりました。
この本は全部で何ページありますか。
この動画を見る
1⃣コップの中のジュースを60%飲んだら、残りは80mLになりました。はじめ、コップの中には、何mLのジュースが入っていましたか。
2⃣所持金の70%を使って本を買ったら、残金は450円になりました。はじめの所持金は何円でしたか。
3⃣ある本を、1日目は全体の$\frac{3}{7}$を読み、2日目は残りの$\frac{5}{6}$を読んだので、残りは24ページありますか。
4⃣ある本を、1日目は全体の$\frac{1}{4}$を読み、2日目は残りの$\frac{2}{3}$を読んだので、残りは60ページになりました。
この本は全部で何ページありますか。
【中学受験算数】【天秤】ゼロから始める中学受験算数20 面積図など不要!天秤法で楽勝!食塩水の濃度計算!!

単元:
#算数(中学受験)#文章題#売買損益と食塩水
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣
(1)6%の食塩水200gに水を▢g加えたら、5%の食塩水になる。
(2)4%の食塩水600gから水を▢g蒸発させると、10%の食塩水になる。
2⃣
(1)9%の食塩水200gに水を▢g加えたら、4%の食塩水になる。
(2)8%の食塩水400gから水を▢g蒸発させると、10%の食塩水になる。
3⃣4%の食塩水200gに食塩を▢g加えたら、20%の食塩水ができる。
4⃣5%の食塩水200gに12%の食塩水を▢g加えたら、7%の食塩水ができる。
この動画を見る
1⃣
(1)6%の食塩水200gに水を▢g加えたら、5%の食塩水になる。
(2)4%の食塩水600gから水を▢g蒸発させると、10%の食塩水になる。
2⃣
(1)9%の食塩水200gに水を▢g加えたら、4%の食塩水になる。
(2)8%の食塩水400gから水を▢g蒸発させると、10%の食塩水になる。
3⃣4%の食塩水200gに食塩を▢g加えたら、20%の食塩水ができる。
4⃣5%の食塩水200gに12%の食塩水を▢g加えたら、7%の食塩水ができる。
【中学受験算数】【食塩水】ゼロから始める中学受験算数19 濃度算の簡単な解き方!まずはここから!

単元:
#算数(中学受験)#文章題#売買損益と食塩水
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣
(1)水100gに食塩を25g加えると、何%の食塩水ができますか。
(2)6%の食塩水を200gつくるには、食塩と水を何gずつ混ぜますか。
(3)30gの食塩を水にとかして12%の食塩水をつくると、何gの食塩水になるか。
2⃣
(1)水90gに食塩を10g加えると、何%の食塩水ができますか。
(2)5%の食塩水を300gつくるには、食塩と水を何gずつ混ぜますか。
(3)35gの食塩を水にとかして14%の食塩水をつくると、何gの食塩水になるか。
3⃣10%の食塩水200gと5%の食塩水300gを混ぜ合わせると、何%の食塩水ができますか。
4⃣5%の食塩水40gと3%の食塩水120gを混ぜ合わせると、何%の食塩水ができますか。
この動画を見る
1⃣
(1)水100gに食塩を25g加えると、何%の食塩水ができますか。
(2)6%の食塩水を200gつくるには、食塩と水を何gずつ混ぜますか。
(3)30gの食塩を水にとかして12%の食塩水をつくると、何gの食塩水になるか。
2⃣
(1)水90gに食塩を10g加えると、何%の食塩水ができますか。
(2)5%の食塩水を300gつくるには、食塩と水を何gずつ混ぜますか。
(3)35gの食塩を水にとかして14%の食塩水をつくると、何gの食塩水になるか。
3⃣10%の食塩水200gと5%の食塩水300gを混ぜ合わせると、何%の食塩水ができますか。
4⃣5%の食塩水40gと3%の食塩水120gを混ぜ合わせると、何%の食塩水ができますか。
【中学受験算数】【損益算】ゼロから始める中学受験算数18 難しい損益算の解き方のコツはこれだけ!!

単元:
#算数(中学受験)#文章題#売買損益と食塩水
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣原価500円の品物に、原価の2割の利益を見込んで定価をつけましたが、売れなかったので、定価の1割引きにして売りました。利益は何円ですか。
2⃣原価800円の品物に、原価の2割5分の利益を見込んで定価をつけましたが、売れなかったので、定価の1割5分引きにして売りました。利益は何円ですか。
3⃣ある商品に、原価の3割の利益を見込んで定価をつけましたが、売れなかったので、定価の2割引きの832円で売りました。
この商品の原価は何円ですか。
4⃣ある商品に、原価の1割5分の利益を見込んで定価をつけましたが、売れなかったので、定価の1割引きの2070円で売りました。
この商品の原価は何円ですか。
5⃣ある品物に、原価の3割増しの定価をつけましたが、売れなかったので、定価の2割引きで売ったところ、1000円の利益がありました。この品物の原価は何円ですか。
6⃣ある品物に、原価の2割増しの定価をつけましたが、売れなかったので、定価の1割引きで売ったところ、96円の利益がありました。この品物の原価は何円ですか。
この動画を見る
1⃣原価500円の品物に、原価の2割の利益を見込んで定価をつけましたが、売れなかったので、定価の1割引きにして売りました。利益は何円ですか。
2⃣原価800円の品物に、原価の2割5分の利益を見込んで定価をつけましたが、売れなかったので、定価の1割5分引きにして売りました。利益は何円ですか。
3⃣ある商品に、原価の3割の利益を見込んで定価をつけましたが、売れなかったので、定価の2割引きの832円で売りました。
この商品の原価は何円ですか。
4⃣ある商品に、原価の1割5分の利益を見込んで定価をつけましたが、売れなかったので、定価の1割引きの2070円で売りました。
この商品の原価は何円ですか。
5⃣ある品物に、原価の3割増しの定価をつけましたが、売れなかったので、定価の2割引きで売ったところ、1000円の利益がありました。この品物の原価は何円ですか。
6⃣ある品物に、原価の2割増しの定価をつけましたが、売れなかったので、定価の1割引きで売ったところ、96円の利益がありました。この品物の原価は何円ですか。
【中学受験算数】【損益算】ゼロから始める中学受験算数17 え!?これだけなの!?損益算の簡単な解き方!!

単元:
#算数(中学受験)#文章題#売買損益と食塩水
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣
(1)原価600円の品物に原価の2割の利益を見込んで定価をつけました。この品物の定価は何円ですか。
(2)ある品物に原価の15%の利益があるように、920円の定価をつけました。この品物の原価は何円ですか。
2⃣
(1)原価800円の品物に原価の2割5分の利益を見込んで定価をつけました。この品物の定価は何円ですか。
(2)ある品物に、原価の16%の利益があるように、522円の定価をつけました。この品物の原価は何円ですか。
3⃣
(1)定価1500円の商品が売れ残ったので、定価の2割引きで売ることにしました。
この商品の売値は何円ですか。
(2)ある商品を、定価の30%引きの630円で売りました。この商品の定価は何円ですか。
4⃣
(1)定価5000円の商品が売れ残ったので、定価の3割引きで売ることにしました。この商品の売値は何円ですか。
(2)ある商品を、定価の45%引きの4400円で買いました。この商品の定価は何円ですか。
この動画を見る
1⃣
(1)原価600円の品物に原価の2割の利益を見込んで定価をつけました。この品物の定価は何円ですか。
(2)ある品物に原価の15%の利益があるように、920円の定価をつけました。この品物の原価は何円ですか。
2⃣
(1)原価800円の品物に原価の2割5分の利益を見込んで定価をつけました。この品物の定価は何円ですか。
(2)ある品物に、原価の16%の利益があるように、522円の定価をつけました。この品物の原価は何円ですか。
3⃣
(1)定価1500円の商品が売れ残ったので、定価の2割引きで売ることにしました。
この商品の売値は何円ですか。
(2)ある商品を、定価の30%引きの630円で売りました。この商品の定価は何円ですか。
4⃣
(1)定価5000円の商品が売れ残ったので、定価の3割引きで売ることにしました。この商品の売値は何円ですか。
(2)ある商品を、定価の45%引きの4400円で買いました。この商品の定価は何円ですか。
【中学受験算数】【割合】ゼロから始める中学受験算数16 最重要単元「割合」が一発で分かる!

単元:
#算数(中学受験)#単位・比と割合・比例・反比例
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣小数は百分率に、百分率は小数にしましょう。
(1)0.673
(2)120%
(3)0.38
(4)0.507
(5)12.5%
(6)105%
2⃣小数は歩合に、歩合は小数にしましょう。
(1)0.298
(2)12割
(3)0.463
(4)1.8
(5)3割2分8厘
(6)15割
3⃣
(1)30mは50mの何倍ですか。
(2)250人の20%は何人ですか。
(3)180円は何円の4割5分ですか。
(4)15kgは60kgの何倍ですか。
(5)800円の3割5分は何円ですか。
(6)50人は何人の40%ですか。
この動画を見る
1⃣小数は百分率に、百分率は小数にしましょう。
(1)0.673
(2)120%
(3)0.38
(4)0.507
(5)12.5%
(6)105%
2⃣小数は歩合に、歩合は小数にしましょう。
(1)0.298
(2)12割
(3)0.463
(4)1.8
(5)3割2分8厘
(6)15割
3⃣
(1)30mは50mの何倍ですか。
(2)250人の20%は何人ですか。
(3)180円は何円の4割5分ですか。
(4)15kgは60kgの何倍ですか。
(5)800円の3割5分は何円ですか。
(6)50人は何人の40%ですか。
【中学受験算数】【平均算】ゼロから始める中学受験算数15 難問もするりと攻略!平均算!

単元:
#算数(中学受験)#文章題#平均算・過不足算・差集め算・消去算
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣あるクラスで算数のテストを行ったところ、男子21人の平均点は76点、女子15人の平均点は88点でした。このクラス全体の平均点は何点ですか。
2⃣ある学校の6年生で体重を調べたところ、男子45人の平均体重は42kg、女子35人の平均体重は38kgでした。6年生全体の平均体重は何kgですか。
3⃣36人のクラスで計算テストを行ったところ、男子の平均点は67点、女子の平均点は76点、クラス全体の平均点は71点でした。このクラスの女子の人数は何人ですか。
4⃣40人のクラスで計算テストを行ったところ、男子の平均点は50点、女子の平均点は60点、クラス全体の平均点は54.5でした。このクラスの女子の人数は何人ですか。
この動画を見る
1⃣あるクラスで算数のテストを行ったところ、男子21人の平均点は76点、女子15人の平均点は88点でした。このクラス全体の平均点は何点ですか。
2⃣ある学校の6年生で体重を調べたところ、男子45人の平均体重は42kg、女子35人の平均体重は38kgでした。6年生全体の平均体重は何kgですか。
3⃣36人のクラスで計算テストを行ったところ、男子の平均点は67点、女子の平均点は76点、クラス全体の平均点は71点でした。このクラスの女子の人数は何人ですか。
4⃣40人のクラスで計算テストを行ったところ、男子の平均点は50点、女子の平均点は60点、クラス全体の平均点は54.5でした。このクラスの女子の人数は何人ですか。
【中学受験算数】【過不足算】ゼロから始める中学受験算数14 図で納得!差集め算・過不足算のちょっとした攻略法!

単元:
#算数(中学受験)#文章題#平均算・過不足算・差集め算・消去算
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣ある本を毎日40ページずつ読んでいくと、24ページずつ読むときよりも4日早く読み終わります。この本は何ページありますか。
2⃣えんぴつを子どもたちに配るのに、1人に5本ずつ配ると3本あまり、1人に7本ずつ配ると13本不足します。子供は何人ですか。また、えんぴつは何本ですか。
3⃣クラス会の費用を集めます。1人から300円ずつ集めると1500円不足し、1人から350円ずつ集めると750円あまります。クラス会の費用は何円ですか。
この動画を見る
1⃣ある本を毎日40ページずつ読んでいくと、24ページずつ読むときよりも4日早く読み終わります。この本は何ページありますか。
2⃣えんぴつを子どもたちに配るのに、1人に5本ずつ配ると3本あまり、1人に7本ずつ配ると13本不足します。子供は何人ですか。また、えんぴつは何本ですか。
3⃣クラス会の費用を集めます。1人から300円ずつ集めると1500円不足し、1人から350円ずつ集めると750円あまります。クラス会の費用は何円ですか。
【中学受験算数】【つるかめ算】ゼロから始める中学受験算数13 つるかめ算がどうしても分からない人必見!仕組みから丁寧に解説します!!

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣1本120円のバラと1本180円のユリを合わせて15本買ったら、代金の合計は2340円でした。
バラは何本買いましたか。
2⃣ツルとカメがいて、頭の数の合計は25で、足の数の合計は80です。ツルは何羽いますか。また、カメは何匹ですか。
3⃣1個30円のみかんと1個80円のりんごを合わせて20個買ったら、代金の合計はちょうど1000円でした。りんごは何個買いましたか。
4⃣52円切手と82円切手を合わせて15枚買って、1050円支払いました。82円切手は何枚買いましたか。
この動画を見る
1⃣1本120円のバラと1本180円のユリを合わせて15本買ったら、代金の合計は2340円でした。
バラは何本買いましたか。
2⃣ツルとカメがいて、頭の数の合計は25で、足の数の合計は80です。ツルは何羽いますか。また、カメは何匹ですか。
3⃣1個30円のみかんと1個80円のりんごを合わせて20個買ったら、代金の合計はちょうど1000円でした。りんごは何個買いましたか。
4⃣52円切手と82円切手を合わせて15枚買って、1050円支払いました。82円切手は何枚買いましたか。
【中学受験算数】【消去算】ゼロから始める中学受験算数12 超分かりやすい消去算のやり方を解説!!

単元:
#算数(中学受験)#文章題#売買損益と食塩水#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣りんご3個とみかん5個では610円、りんご2個とみかん3個では390円です。りんごとみかんはそれぞれ1個何円ですか。
2⃣ノート2冊とえんぴつ5本では640円、ノート4冊とえんぴつ3本では720円です。えんぴつ1本のねだんは何円ですか。
3⃣ボールペン1本のねだんはえんぴつ1本のねだんより70円高く、えんぴつ4本とボールペン1本では470円です。えんぴつとボールペンは、それぞれ1本何円ですか。
4⃣ノート2冊とえんぴつ5本を買うと480円です。ノート2冊のねだんとえんぴつ3本のねだんは同じです。
ノート1冊のねだんは何円ですか。
この動画を見る
1⃣りんご3個とみかん5個では610円、りんご2個とみかん3個では390円です。りんごとみかんはそれぞれ1個何円ですか。
2⃣ノート2冊とえんぴつ5本では640円、ノート4冊とえんぴつ3本では720円です。えんぴつ1本のねだんは何円ですか。
3⃣ボールペン1本のねだんはえんぴつ1本のねだんより70円高く、えんぴつ4本とボールペン1本では470円です。えんぴつとボールペンは、それぞれ1本何円ですか。
4⃣ノート2冊とえんぴつ5本を買うと480円です。ノート2冊のねだんとえんぴつ3本のねだんは同じです。
ノート1冊のねだんは何円ですか。
元大手塾講師の過去問解説!(清心中学校 平成28年1次B日程 算数)

単元:
#算数(中学受験)#文章題#売買損益と食塩水#速さ#速さその他#場合の数#場合の数
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣
(1)⑤ $1 \frac{1}{4} - \frac{1}{6} +3 \frac{1}{2}$
(2)$(\frac{3}{2} - ▢)÷ \frac{3}{4} = \frac{2}{3}$
(3)ゆいさんは880円、ゆきこさんは460円持っています。ゆいさんがゆきこさんにいくらわたすと2人の金額が同じになりますか。
2⃣こころさんは所持金の$\frac{3}{5}$を使い、さらに残ったお金の$\frac{1}{4}$を使うと残金が360円になりました。
所持金はいくらですか。
3⃣あるテストで10人の生徒の平均点が60点で、このうち男子6人の平均点が54点でした。女子4人の平均点を求めなさい。
4⃣あい子さんのお父さんは、ガソリン1LあたりI0km走る自動車で、1か月に1200km走ります。
ガソリン代を1Lあたり160円として、次の各問いにこたえなさい。
(1)1か月のガソリン代はいくらですか。
(2)お父さんが新しく買おうとしている自動車で同じ距離を走ると、1か月あたり6400円節約することができます。この自動車はガソリン1Lあたり何km走りますか。
5⃣分速100mの速さで行けば目的地に予定時刻より2分早く着き、分速60mの速さで行くと予定時刻より2分早く着き、分速60mの速さで行くと予定時刻より5分遅く着きます。
この時、次の各問いに答えなさい。
(1)次のア~オに当てはまる数値を求めなさい。
分速100mで行けば、予定時刻には目的地より㋐m先に行っており、分速60mだと予定時刻には目的地の手前㋑mの地点まで行く。
つまり、分速100mと分速60mで行った時では(㋐+㋑)mの差ができる。
また、分速100mと分速60mでは、1分間に㋒mの差が生じる。
以上より、目的地に着くまでの予定時間は ㋓分㋔秒と求められる。
(2)予定通り着くには分速何mの速さで行けばよいですか?
6⃣袋の中に赤玉、白玉合わせて200個人っています。
赤玉は全体の12%になります。このとき、次の各問いに答えなさい。
(1)赤玉の個数を求めなさい。
(2)この袋の中から白玉50個を取り出すと、赤玉は全体の何%になりますか。
(3)この袋の中に白玉をいくつか加えて、赤玉の個数を全体の5%にしたい。
何個の白玉を加えればよいですか。
この動画を見る
1⃣
(1)⑤ $1 \frac{1}{4} - \frac{1}{6} +3 \frac{1}{2}$
(2)$(\frac{3}{2} - ▢)÷ \frac{3}{4} = \frac{2}{3}$
(3)ゆいさんは880円、ゆきこさんは460円持っています。ゆいさんがゆきこさんにいくらわたすと2人の金額が同じになりますか。
2⃣こころさんは所持金の$\frac{3}{5}$を使い、さらに残ったお金の$\frac{1}{4}$を使うと残金が360円になりました。
所持金はいくらですか。
3⃣あるテストで10人の生徒の平均点が60点で、このうち男子6人の平均点が54点でした。女子4人の平均点を求めなさい。
4⃣あい子さんのお父さんは、ガソリン1LあたりI0km走る自動車で、1か月に1200km走ります。
ガソリン代を1Lあたり160円として、次の各問いにこたえなさい。
(1)1か月のガソリン代はいくらですか。
(2)お父さんが新しく買おうとしている自動車で同じ距離を走ると、1か月あたり6400円節約することができます。この自動車はガソリン1Lあたり何km走りますか。
5⃣分速100mの速さで行けば目的地に予定時刻より2分早く着き、分速60mの速さで行くと予定時刻より2分早く着き、分速60mの速さで行くと予定時刻より5分遅く着きます。
この時、次の各問いに答えなさい。
(1)次のア~オに当てはまる数値を求めなさい。
分速100mで行けば、予定時刻には目的地より㋐m先に行っており、分速60mだと予定時刻には目的地の手前㋑mの地点まで行く。
つまり、分速100mと分速60mで行った時では(㋐+㋑)mの差ができる。
また、分速100mと分速60mでは、1分間に㋒mの差が生じる。
以上より、目的地に着くまでの予定時間は ㋓分㋔秒と求められる。
(2)予定通り着くには分速何mの速さで行けばよいですか?
6⃣袋の中に赤玉、白玉合わせて200個人っています。
赤玉は全体の12%になります。このとき、次の各問いに答えなさい。
(1)赤玉の個数を求めなさい。
(2)この袋の中から白玉50個を取り出すと、赤玉は全体の何%になりますか。
(3)この袋の中に白玉をいくつか加えて、赤玉の個数を全体の5%にしたい。
何個の白玉を加えればよいですか。
【中学受験算数】【分配算】ゼロから始める中学受験算数11 わかる!和差算・分配算!

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣和が52、差が16である2つの整数を求めよ。
2⃣和が116差が18である2つの整数を求めよ。
3⃣A,B,C3つの数があり、その和は378です。
BはAより2大きく、CはBより5大きいとき、Aはいくつですか。
4⃣60個のおはじきを姉と妹で分けたら、姉の個数は妹の個数の3倍よりも4個多くなりました。姉の個数は何個ですか。
5⃣90枚のカードを兄と弟で分けたら、兄の枚数は弟の枚数の2倍よりも6枚多くなりました。2人のカードはそれぞれ何枚ですか。
この動画を見る
1⃣和が52、差が16である2つの整数を求めよ。
2⃣和が116差が18である2つの整数を求めよ。
3⃣A,B,C3つの数があり、その和は378です。
BはAより2大きく、CはBより5大きいとき、Aはいくつですか。
4⃣60個のおはじきを姉と妹で分けたら、姉の個数は妹の個数の3倍よりも4個多くなりました。姉の個数は何個ですか。
5⃣90枚のカードを兄と弟で分けたら、兄の枚数は弟の枚数の2倍よりも6枚多くなりました。2人のカードはそれぞれ何枚ですか。
【中学受験算数】【数列】ゼロから始める中学受験算数10 数列を徹底攻略!!!

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣次の数列の$\boxed ア$、$\boxed イ$にあてはまる数を答えましょう。
(1)2,4,6,$\boxed ア$,10,12,$\boxed イ$,16・・・
(2)1,2,4,7,11,16,$\boxed ア$,$\boxed イ$,37・・・
(3)1,4,9,$\boxed ア$,25,36,$\boxed イ$,64,81・・・
(4)1,1,2,3,5,8,$\boxed ア$,21,$\boxed イ$,55・・・
2⃣次の数列の$\boxed ア$,$\boxed イ$にあてはまる数を答えましょう。
(1)1,8,27,$\boxed ア$,125,216,$\boxed イ$,512・・・
(2)6,7,13,20,$\boxed ア$,53,86,$\boxed イ$,225・・・
3⃣4,7,10,13,16,19,22,25・・・という数列で
(1)|5|は左から何番目ですか。
(2)はじめから30番目までの和はいくつですか。
4⃣1,5,9,13,17,21,25,29・・・という数列で
(1)左から25番目の数はいくつですか。
(2)149は左から何番目の数ですか。
(3)はじめの数から100番目の数までの和を求めましょう。
この動画を見る
1⃣次の数列の$\boxed ア$、$\boxed イ$にあてはまる数を答えましょう。
(1)2,4,6,$\boxed ア$,10,12,$\boxed イ$,16・・・
(2)1,2,4,7,11,16,$\boxed ア$,$\boxed イ$,37・・・
(3)1,4,9,$\boxed ア$,25,36,$\boxed イ$,64,81・・・
(4)1,1,2,3,5,8,$\boxed ア$,21,$\boxed イ$,55・・・
2⃣次の数列の$\boxed ア$,$\boxed イ$にあてはまる数を答えましょう。
(1)1,8,27,$\boxed ア$,125,216,$\boxed イ$,512・・・
(2)6,7,13,20,$\boxed ア$,53,86,$\boxed イ$,225・・・
3⃣4,7,10,13,16,19,22,25・・・という数列で
(1)|5|は左から何番目ですか。
(2)はじめから30番目までの和はいくつですか。
4⃣1,5,9,13,17,21,25,29・・・という数列で
(1)左から25番目の数はいくつですか。
(2)149は左から何番目の数ですか。
(3)はじめの数から100番目の数までの和を求めましょう。
【中学受験算数】【分数】ゼロから始める中学受験算数9 小数と分数の問題はこれだけでOK!!

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣$\frac{3}{7},0.45,\frac{4}{9},\frac{2}{5}$を小さいほうから順に並べましょう。
2⃣$\frac{7}{9},0.78,\frac{11}{15},\frac{5}{7},\frac{8}{11}$を小さいほうから順に並べましょう。
3⃣$\frac{3}{10}$と$\frac{5}{12}$の間にあり、分母が5である分数を求めましょう。
4⃣$\frac{3}{4}$と$\frac{8}{9}$の間にあり、分母が6である分数を求めましょう。
5⃣分母と分子の和が102で約分すると$\frac{2}{15}$になる分数を求めましょう。
6⃣分母と分子の和が238で約分すると$\frac{3}{11}$になる分数を求めましょう。
この動画を見る
1⃣$\frac{3}{7},0.45,\frac{4}{9},\frac{2}{5}$を小さいほうから順に並べましょう。
2⃣$\frac{7}{9},0.78,\frac{11}{15},\frac{5}{7},\frac{8}{11}$を小さいほうから順に並べましょう。
3⃣$\frac{3}{10}$と$\frac{5}{12}$の間にあり、分母が5である分数を求めましょう。
4⃣$\frac{3}{4}$と$\frac{8}{9}$の間にあり、分母が6である分数を求めましょう。
5⃣分母と分子の和が102で約分すると$\frac{2}{15}$になる分数を求めましょう。
6⃣分母と分子の和が238で約分すると$\frac{3}{11}$になる分数を求めましょう。
【中学受験算数】【整数】ゼロから始める中学受験算数8 ややこしさを瞬殺!整数の問題を攻略せよ!!(上級問題)

単元:
#算数(中学受験)#計算と数の性質#約数・倍数を利用する問題
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣18と34のどちらをわっても2あまる整数をすべて求めましょう。
2⃣118と82のどちらをわっても10あまる整数をすべて求めましょう。
3⃣7でわっても4でわっても3あまる整数のうち、100にいちばん近い数を求めよ。
4⃣4でわっても6でわっても1あまる整数のうち、100にいちばん近い数を求めよ。
5⃣○○○○○は0、○○○○●は1、○○○●○は2、○○○●●は3、○○●○○は4、
○○●○●は5、○●○○○は8、○●○●○は10
(1)●○●○●はいくつ?
(2)30を5つの○に色をぬって表しましょう。
6⃣○○○○○は0、△○○○○は1、○△○○○は2、○○△○○は4、△○○△○は9、
○○△○△は20
(1)○△△△○はいくつ?
(2)27を○と△を5個すべて表しましょう。
この動画を見る
1⃣18と34のどちらをわっても2あまる整数をすべて求めましょう。
2⃣118と82のどちらをわっても10あまる整数をすべて求めましょう。
3⃣7でわっても4でわっても3あまる整数のうち、100にいちばん近い数を求めよ。
4⃣4でわっても6でわっても1あまる整数のうち、100にいちばん近い数を求めよ。
5⃣○○○○○は0、○○○○●は1、○○○●○は2、○○○●●は3、○○●○○は4、
○○●○●は5、○●○○○は8、○●○●○は10
(1)●○●○●はいくつ?
(2)30を5つの○に色をぬって表しましょう。
6⃣○○○○○は0、△○○○○は1、○△○○○は2、○○△○○は4、△○○△○は9、
○○△○△は20
(1)○△△△○はいくつ?
(2)27を○と△を5個すべて表しましょう。
甲陽学院高校 整数問題 高校入試

単元:
#算数(中学受験)#数学(中学生)#中3数学#平方根#過去問解説(学校別)#甲陽学院中学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$S_n=1!+2!+3!+…+n!$
$S_n$が平方数となる$n$を全て求めよ
(1)
$5!$を求めよ
$S_{10}$の1の位
出典:甲陽学院高等学校 入試問題
この動画を見る
$S_n=1!+2!+3!+…+n!$
$S_n$が平方数となる$n$を全て求めよ
(1)
$5!$を求めよ
$S_{10}$の1の位
出典:甲陽学院高等学校 入試問題
【受験算数】小数・分数:分数を分子1の足し算に分ける問題
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\dfrac{3}{5}=\dfrac{1}{ア}+\dfrac{1}{イ}$のときア、イに当てはまる整数を求めなさ。ただし、$ア\ltイ$する。
この動画を見る
$\dfrac{3}{5}=\dfrac{1}{ア}+\dfrac{1}{イ}$のときア、イに当てはまる整数を求めなさ。ただし、$ア\ltイ$する。
中学入試問題 駒場東邦 整数問題

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#過去問解説(学校別)#駒場東邦中学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$121 \times 122 \times 123 \times 124 \times 125 \times 126 \times 127 \times$
$ 128 \times 129 \times 130$
1の位から順にみて最初に現れる0以外の数字は?
出典:駒場東邦中学校 過去問
この動画を見る
$121 \times 122 \times 123 \times 124 \times 125 \times 126 \times 127 \times$
$ 128 \times 129 \times 130$
1の位から順にみて最初に現れる0以外の数字は?
出典:駒場東邦中学校 過去問
【受験算数】 穴のあき方:64個の小さな立方体で作られた大きな立方体にあけられた穴の個数を求める方法を解説!

単元:
#算数(中学受験)#立体図形#立体図形その他
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
64個の小さな立方体で右図のような大きな立方体を作ります。つきぬける穴を図のようにあけたとき、おのおのの小さな立方体について、1つも穴のあいていない立方体、1方向あいている立方体、2方向あいている立方体、3方向あいている立方体はそれぞれいくつあるか求めなさい。
この動画を見る
64個の小さな立方体で右図のような大きな立方体を作ります。つきぬける穴を図のようにあけたとき、おのおのの小さな立方体について、1つも穴のあいていない立方体、1方向あいている立方体、2方向あいている立方体、3方向あいている立方体はそれぞれいくつあるか求めなさい。
【受験算数】循環小数(応用):0.481818181…の分数を小数で表すには!?

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の小数を分数で表しなさい。(3)$0.481818181…$
但し、$\dfrac{1}{9}=0.1111…、\dfrac{1}{99}=0.010101…、\dfrac{1}{999}=0.001001001…$を利用する
この動画を見る
次の小数を分数で表しなさい。(3)$0.481818181…$
但し、$\dfrac{1}{9}=0.1111…、\dfrac{1}{99}=0.010101…、\dfrac{1}{999}=0.001001001…$を利用する
【受験算数】数の性質:1×2×3×4×...×100 この数3で何回割れるでしょう?

単元:
#算数(中学受験)#計算と数の性質#数の性質その他
指導講師:
理数個別チャンネル
問題文全文(内容文):
①1~100まで掛け算した答えを3で割っていくと何回割ることができるか
②1~50まで掛け算した答えには0が何個並ぶのか
この動画を見る
①1~100まで掛け算した答えを3で割っていくと何回割ることができるか
②1~50まで掛け算した答えには0が何個並ぶのか
開成中学 整数 等差数列の和

単元:
#算数(中学受験)#数列#数列とその和(等差・等比・階差・Σ)#過去問解説(学校別)#数学(高校生)#数B#開成中学
指導講師:
鈴木貫太郎
問題文全文(内容文):
平方数を3つ以上の連続数の和で表す
(例)$6^2=1+2+3+…+8=11+12+13$
(1)
$7^2$
(2)
$10^2$
(3)
$30^2$は何通りあるか
出典:2018年開成中学校 過去問
この動画を見る
平方数を3つ以上の連続数の和で表す
(例)$6^2=1+2+3+…+8=11+12+13$
(1)
$7^2$
(2)
$10^2$
(3)
$30^2$は何通りあるか
出典:2018年開成中学校 過去問
リクエスト頂いた規則性やっていきましょう【中学受験】
単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
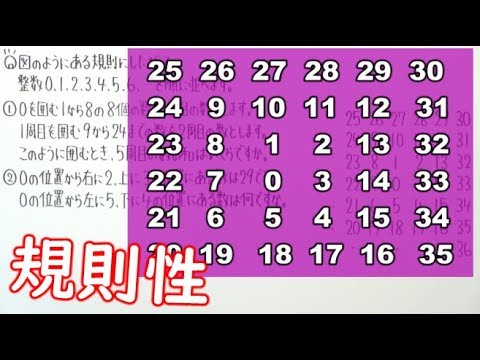
図のようにある規則にしたがって、整数0.1.2.3.4.5.6...を順に並べます。
①
0を囲む1から8の8個の数を1周目の数とします。
1周目を囲む9から24までの数を2周目の数とします。
このように囲むとき、5周目の数の和はいくらですか。
②
0の位置から右に2、上に3の位置にある数は29です。
0の位置から左に5、下に4の位置にある数は何ですか。
この動画を見る
図のようにある規則にしたがって、整数0.1.2.3.4.5.6...を順に並べます。
①
0を囲む1から8の8個の数を1周目の数とします。
1周目を囲む9から24までの数を2周目の数とします。
このように囲むとき、5周目の数の和はいくらですか。
②
0の位置から右に2、上に3の位置にある数は29です。
0の位置から左に5、下に4の位置にある数は何ですか。
中学入試の問題をやってみます【お試し】

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$12×(\frac{1}{2}-\frac{1}{3})-(\frac{1}{2}\div 0.75-\frac{4}{9})×9$
②$93-89+83-71+59-53+50-47+41-29+17-11+7$
③$(954-459-25×16+0.4)\div(\frac{1}{12}+\frac{1}{84}+\frac{1}{210}) $
④$(0.375×24+2.5×0.625×16)×19-25×12-125×16-1.4×190$
⑤$1×1×1+3+5+3×3×3+13+15+17+19+5×5×5+31+33+35+37+39+41$
この動画を見る
①$12×(\frac{1}{2}-\frac{1}{3})-(\frac{1}{2}\div 0.75-\frac{4}{9})×9$
②$93-89+83-71+59-53+50-47+41-29+17-11+7$
③$(954-459-25×16+0.4)\div(\frac{1}{12}+\frac{1}{84}+\frac{1}{210}) $
④$(0.375×24+2.5×0.625×16)×19-25×12-125×16-1.4×190$
⑤$1×1×1+3+5+3×3×3+13+15+17+19+5×5×5+31+33+35+37+39+41$
