 算数(中学受験)
算数(中学受験)
 算数(中学受験)
算数(中学受験)
シンプル過ぎ!でも解けない!?そのヤバ過ぎる解法○○とは!?【中学受験算数】【入試問題】【算数オリンピック】
単元:
#算数(中学受験)#平面図形#角度と面積#その他#算数オリンピック#慶應義塾普通部
指導講師:
こばちゃん塾
問題文全文(内容文):
2021桜美林中学校
下図のように正三角形の紙を折った。
角㋐は何度?
2021慶應義塾普通部
下図は正五角形と正八角形を1辺を重ね合わせてかいたものです。
㋐、㋑は何度?
2009算数オリンピック トライアル
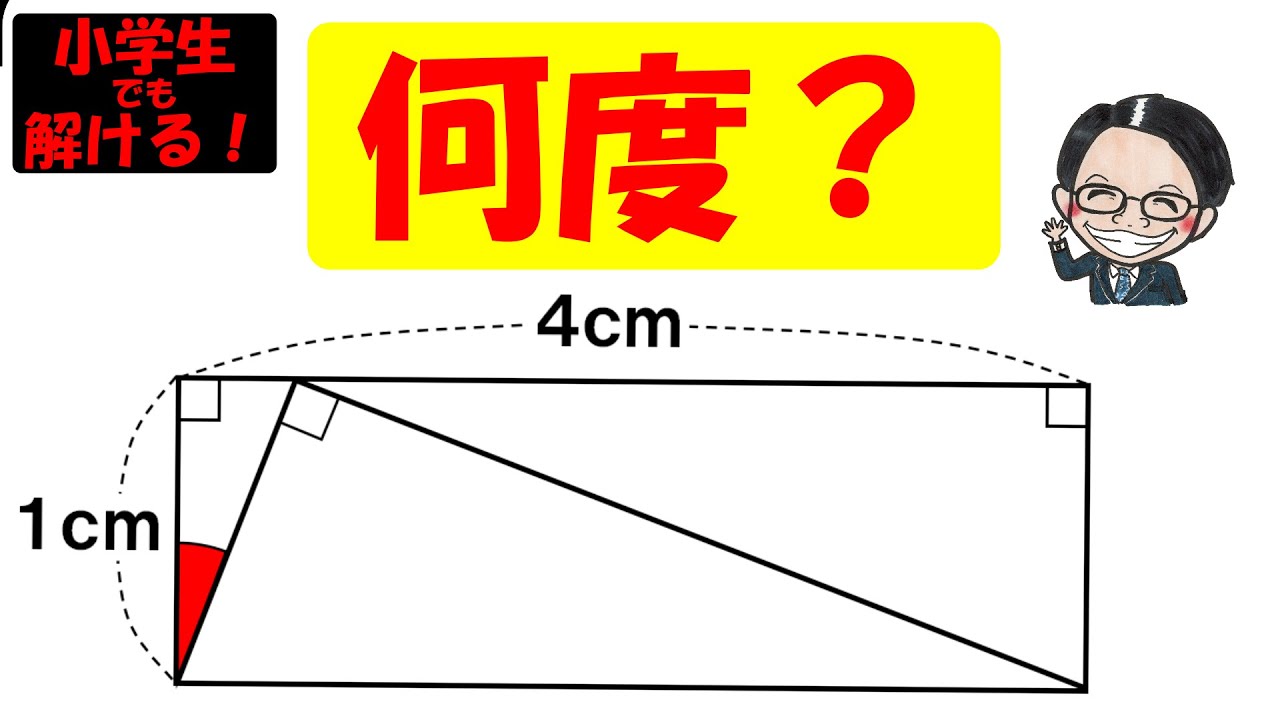
下図の長方形ABCDで、xは何度?
*図は動画内参照
この動画を見る
2021桜美林中学校
下図のように正三角形の紙を折った。
角㋐は何度?
2021慶應義塾普通部
下図は正五角形と正八角形を1辺を重ね合わせてかいたものです。
㋐、㋑は何度?
2009算数オリンピック トライアル
下図の長方形ABCDで、xは何度?
*図は動画内参照
【小3算数-9】時こくと時間は何がちがうの?

単元:
#算数(中学受験)#文章題#単位・比と割合・比例・反比例
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
算数(時こくと時間は何がちがうの?)
ポイント
好きなテレビ番組は(午後6時)から始まって、(30分間)放送される
①家から学校まで歩くと40分かかります。
家を7時30分に出るとき学校に着く時こくは何時何分ですか。
②ぼくの家から公園まで15分かかります。
公園に2時40分に着くには、家を何時何分に出ればいいかな。
この動画を見る
算数(時こくと時間は何がちがうの?)
ポイント
好きなテレビ番組は(午後6時)から始まって、(30分間)放送される
①家から学校まで歩くと40分かかります。
家を7時30分に出るとき学校に着く時こくは何時何分ですか。
②ぼくの家から公園まで15分かかります。
公園に2時40分に着くには、家を何時何分に出ればいいかな。
【受験算数】数の性質:約数を4つ持つ数 その2【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#予習シ#予習シ算数・小5下#中学受験教材#整数の分解と構成
指導講師:
理数個別チャンネル
問題文全文(内容文):
約数を4つ持つ数の中で、21は何番目に大きい数か求めよ。【予習シリーズ 6年生】
この動画を見る
約数を4つ持つ数の中で、21は何番目に大きい数か求めよ。【予習シリーズ 6年生】
【受験算数】数の性質:約数を4つ持つ数 その1【予習シリーズ算数・小5下】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#予習シ#予習シ算数・小5下#中学受験教材#整数の分解と構成
指導講師:
理数個別チャンネル
問題文全文(内容文):
約数を4つ持つ数はどんな数かを考えましょう。
この動画を見る
約数を4つ持つ数はどんな数かを考えましょう。
計算の裏技

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$25 \times 36 =$
この問題を一瞬で解く方法紹介動画です
この動画を見る
$25 \times 36 =$
この問題を一瞬で解く方法紹介動画です
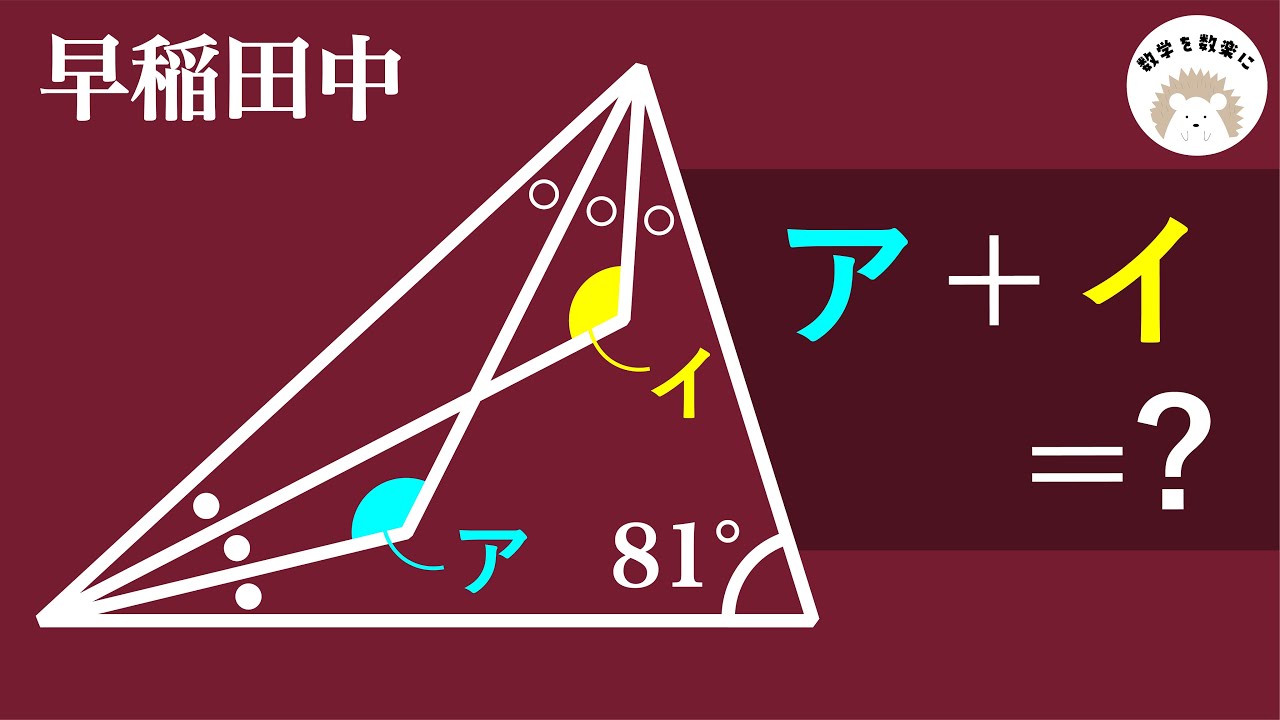
受験算数 角の和 早稲田中
【受験算数】規則性に関する問題:(基本❹)四角数の基本【予習シリーズ演習問題集・小5下】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#予習シ#予習シ演問・小5下#中学受験教材#規則性に関する問題
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図のように、1から順に整数を並べていきます。これについて、次の問いに答えなさい。
(1)1段目の20列目の数はいくつですか?
(2)20段目の10列目の数はいくつですか。(3)250は何段目の何列目の数ですか。
この動画を見る
右の図のように、1から順に整数を並べていきます。これについて、次の問いに答えなさい。
(1)1段目の20列目の数はいくつですか?
(2)20段目の10列目の数はいくつですか。(3)250は何段目の何列目の数ですか。
【受験算数】規則性に関する問題:(基本❸)三角数の基本【予習シリーズ演習問題集・小5下】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#予習シ#予習シ演問・小5下#中学受験教材#規則性に関する問題
指導講師:
理数個別チャンネル
問題文全文(内容文):
右のように、あるきまりに従って整数が書かれたカードを並べました。これについて、次の問いに答えなさい。
(1)90は何段目の左から何番目にありますか。
(2)15段目にある数をすべて加えると、その和はいくつになりますか。
この動画を見る
右のように、あるきまりに従って整数が書かれたカードを並べました。これについて、次の問いに答えなさい。
(1)90は何段目の左から何番目にありますか。
(2)15段目にある数をすべて加えると、その和はいくつになりますか。
【受験算数】規則性に関する問題:(基本❷)余りによる規則性【予習シリーズ演習問題集・小5下】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#予習シ#予習シ演問・小5下#中学受験教材#規則性に関する問題
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の表は、あるきまりに従って整数を1から順に並べたものです。例えば、2段目の4列目の数は11です。これについて、次の問いに答えなさい。
(1)60は何段目の何列目にありますか。
(2)3列目の数を3+10+17+...と順に18段目の数までを加えると、その和はいくつになりますか。
(3)16段目にある7個の数をすべて加えると、その和はいくつになりますか。
この動画を見る
右の表は、あるきまりに従って整数を1から順に並べたものです。例えば、2段目の4列目の数は11です。これについて、次の問いに答えなさい。
(1)60は何段目の何列目にありますか。
(2)3列目の数を3+10+17+...と順に18段目の数までを加えると、その和はいくつになりますか。
(3)16段目にある7個の数をすべて加えると、その和はいくつになりますか。
【図形問題裏技】これだけで算数の図形偏差値20アップ!?嘘みたいにスラスラ解けちゃう禁断の裏技全て公開!あなたもたった1時間で図形マスター!【永久保存版】【神回】

単元:
#算数(中学受験)#平面図形#角度と面積#相似と相似を利用した問題#図形の移動#平面図形その他
指導講師:
こばちゃん塾
問題文全文(内容文):
例題
小さい円の回転数は?
*図は動画内参照
この動画を見る
例題
小さい円の回転数は?
*図は動画内参照
公約数の個数の求め方とは?

単元:
#計算と数の性質#数の性質その他#数学(中学生)#約数・倍数を利用する問題#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
360と660の公約数は全部で何個?
開明高等学校
この動画を見る
360と660の公約数は全部で何個?
開明高等学校
【小3算数-8】3けたの筆算②(チャレンジ編)

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
算数(3けたの筆算②・チャレンジ編)
Q.筆算でやろう!
①829+305
②6251-1927
③834-735
④1234+5678
⑤8+796
⑥5030-49
⑦1000-372
⑧30150-19275
この動画を見る
算数(3けたの筆算②・チャレンジ編)
Q.筆算でやろう!
①829+305
②6251-1927
③834-735
④1234+5678
⑤8+796
⑥5030-49
⑦1000-372
⑧30150-19275
簡単に解けるのに発想が浮かばない難問!底辺も高さも分からないのに面積が求められるって本当!?【中学受験算数】【サレジオ学院中】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#灘中学校
指導講師:
こばちゃん塾
問題文全文(内容文):
2021灘中学校
太線内の面積は?
2021灘中学校
下図で三角形ABCの面積が80㎠のとき、GFの長さは、BGの長さの何倍?
2021サレジオ学院中学校
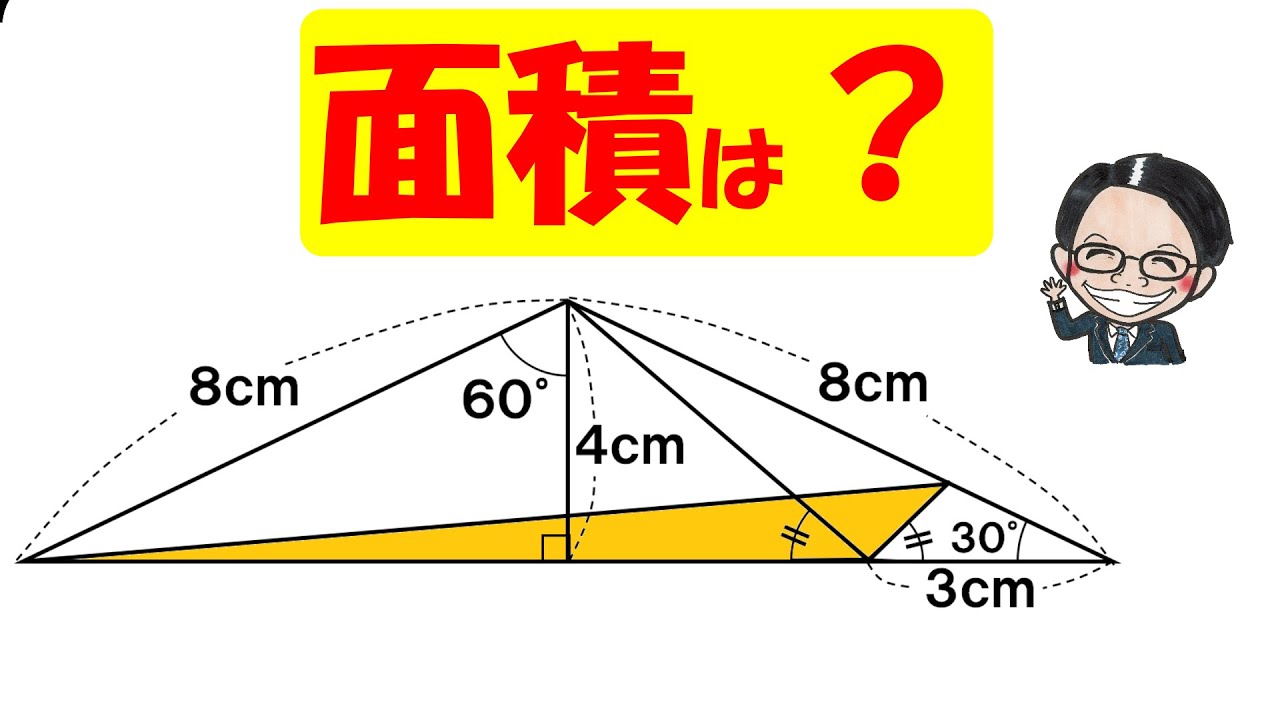
60°の角をはさむ辺の長さが8㎝、4㎝の三角形を2つ使って、下図のような二等辺三角形ABCを作る。三角形BDEの面積は?
*図は動画内参照
この動画を見る
2021灘中学校
太線内の面積は?
2021灘中学校
下図で三角形ABCの面積が80㎠のとき、GFの長さは、BGの長さの何倍?
2021サレジオ学院中学校
60°の角をはさむ辺の長さが8㎝、4㎝の三角形を2つ使って、下図のような二等辺三角形ABCを作る。三角形BDEの面積は?
*図は動画内参照
【小3算数-7】3けたの筆算①

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
算数(3けたの筆算①)
注意)529+13を筆算でかくとき・・
①52+74
②352+174
③629+83
④356-143
⑤530-231
⑥700-63
この動画を見る
算数(3けたの筆算①)
注意)529+13を筆算でかくとき・・
①52+74
②352+174
③629+83
④356-143
⑤530-231
⑥700-63
これ小学生でも解けるって本当!?○○が分かっていれば超きもち良く解けます!!【中学受験算数】【入試問題】【算数オリンピック】
単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#角度と面積#その他#海城中学#算数オリンピック#逗子開成中学
指導講師:
こばちゃん塾
問題文全文(内容文):
2021逗子開成中学校
四角形ABCDは長方形です。
おうぎ形ODEの面積は?(円周率は3.14)
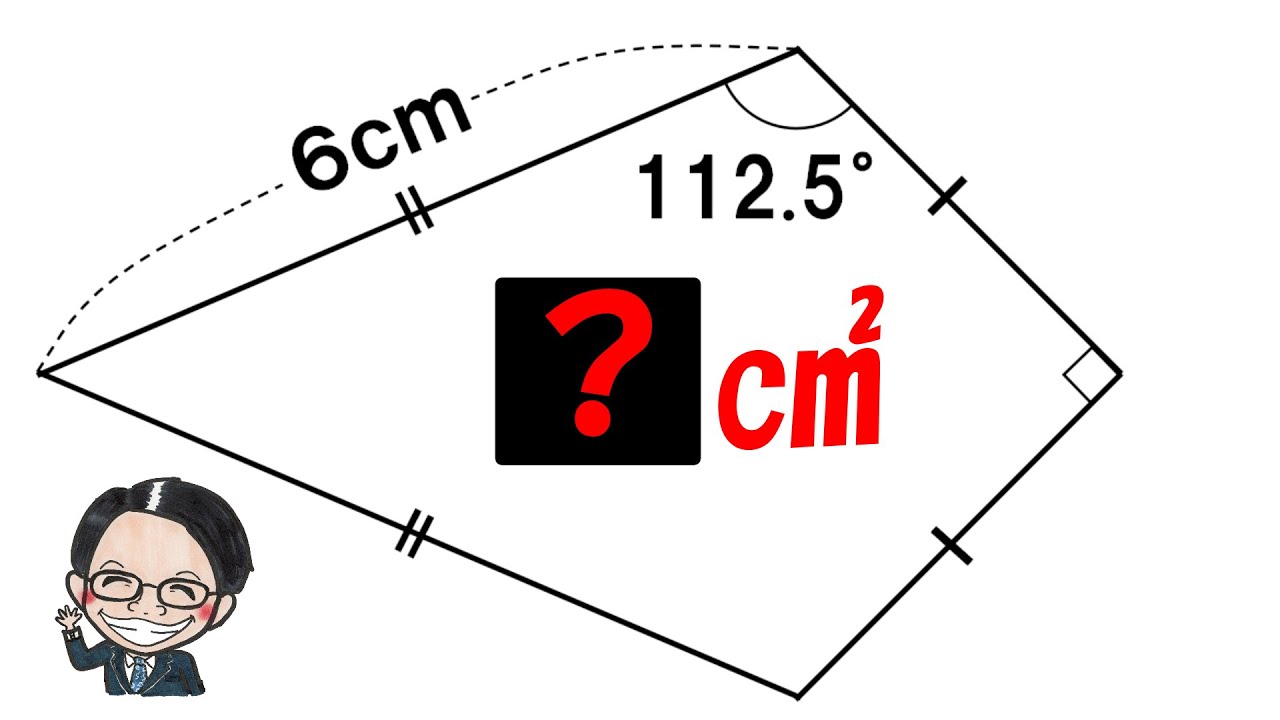
2021海城中学校
下図は半径12㎝の円の円周を12等分したものです。四角形ABCDの面積は?
2013算数オリンピックファイナル(改題)
四角形ABCDの面積は?
*図は動画内参照
この動画を見る
2021逗子開成中学校
四角形ABCDは長方形です。
おうぎ形ODEの面積は?(円周率は3.14)
2021海城中学校
下図は半径12㎝の円の円周を12等分したものです。四角形ABCDの面積は?
2013算数オリンピックファイナル(改題)
四角形ABCDの面積は?
*図は動画内参照
高校生が今すぐするべき勉強とは?~ここみらい×あきとんとん~

早稲田(教)基本問題

単元:
#約数・倍数を利用する問題#大学入試過去問(数学)#早稲田大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$1~15n$の整数のうち3の倍数でも5の倍数でもない数の総和を求めよ.
早稲田(教)過去問
この動画を見る
$1~15n$の整数のうち3の倍数でも5の倍数でもない数の総和を求めよ.
早稲田(教)過去問
【道は一筋なり!】文章題:明治学院東村山高等学校~全国入試問題解法
単元:
#数学(中学生)#文章題#売買損益と食塩水#文章題その他#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
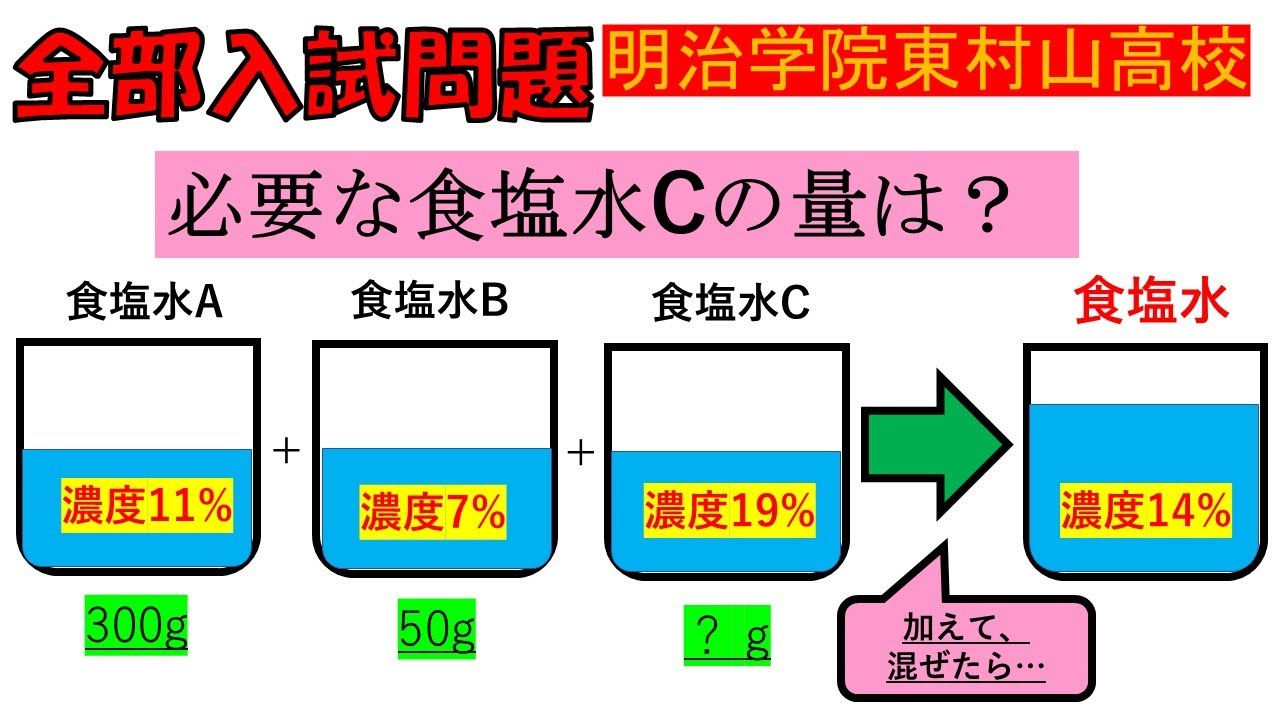
問題文全文(内容文):
必要な食塩水$C$の量は?
明治学院東村山高等学校過去問
この動画を見る
必要な食塩水$C$の量は?
明治学院東村山高等学校過去問
小学生版どっちがでかい?

単元:
#算数(中学受験)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 1$ VS $\dfrac{17}{52}+\dfrac{37}{112}+\dfrac{57}{172}$
どちらが大きい?
この動画を見る
$ 1$ VS $\dfrac{17}{52}+\dfrac{37}{112}+\dfrac{57}{172}$
どちらが大きい?
【数学習いながら英語を教える人】円錐の体積と表面積【もりてつ数検への道】

単元:
#算数(中学受験)#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師:
Morite2 English Channel
問題文全文(内容文):
鈴木貫太郎先生が、円錐の体積と表面積の求め方を解説します。
公式の意味を考えて使ってみましょう!
この動画を見る
鈴木貫太郎先生が、円錐の体積と表面積の求め方を解説します。
公式の意味を考えて使ってみましょう!
【小3算数-6】図を使ってかくれた数を考えよう

単元:
#算数(中学受験)#計算と数の性質#平均算・過不足算・差集め算・消去算
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
算数(図を使ってかくれた数を考えよう)
ポイント
問題に登場するものをチェックして、①と➁からかいていこう!
Q.図をかいてやってみよう!
③あめとガムとチョコを買いに行ったら 全部で90円かかりました。
あめは10円、ガムは20円でした。チョコは何円でしたか?
④お皿の上にチョコがたくさんあります。 その中の7こをぼくが食べました。
そのあと、妹が5こ食べたら、のこりは16こになりました。
はじめにチョコは何こありましたか?
この動画を見る
算数(図を使ってかくれた数を考えよう)
ポイント
問題に登場するものをチェックして、①と➁からかいていこう!
Q.図をかいてやってみよう!
③あめとガムとチョコを買いに行ったら 全部で90円かかりました。
あめは10円、ガムは20円でした。チョコは何円でしたか?
④お皿の上にチョコがたくさんあります。 その中の7こをぼくが食べました。
そのあと、妹が5こ食べたら、のこりは16こになりました。
はじめにチョコは何こありましたか?
これ以外の解き方があったら教えてください!全5つの解き方を一気に解説!これ、小学生が解くってマジ・・・。難しすぎでしょ!【ジュニア算数オリンピック】【難問】
単元:
#算数(中学受験)#その他#算数オリンピック
指導講師:
こばちゃん塾
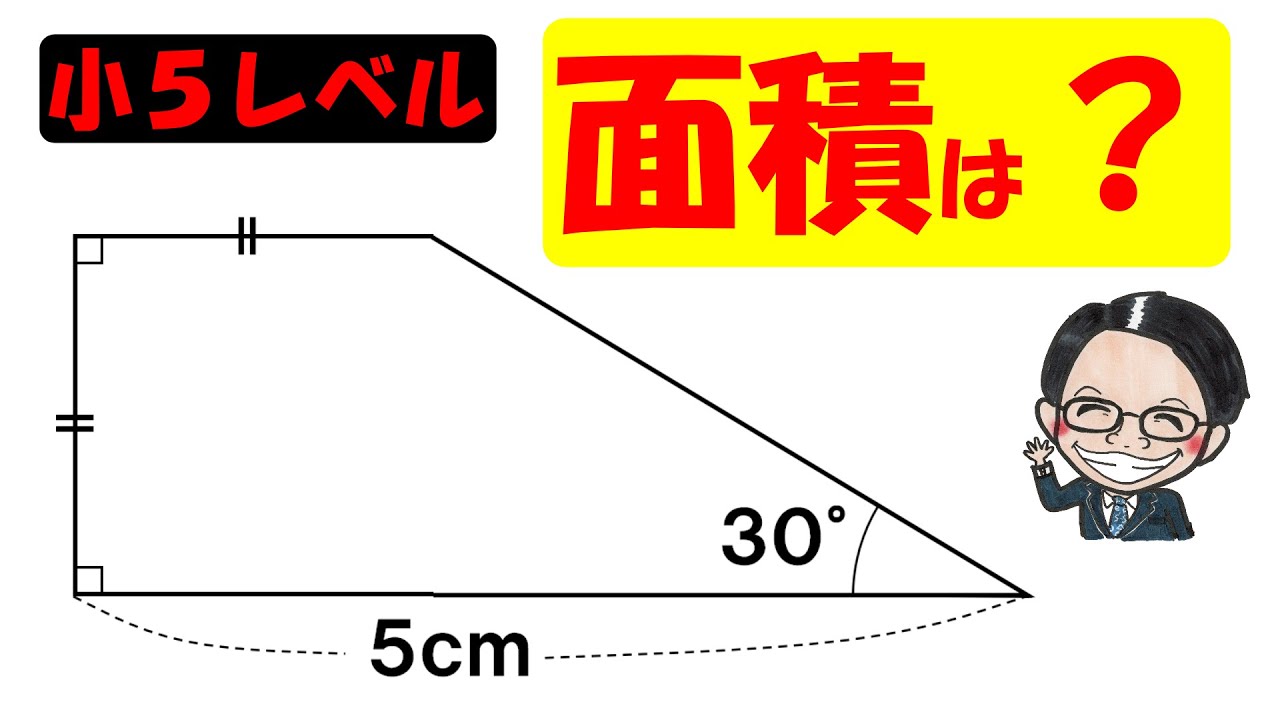
問題文全文(内容文):
ジュニア算数オリンピック2018ファイナル
台形ABCDの面積は?
*図は動画内参照
この動画を見る
ジュニア算数オリンピック2018ファイナル
台形ABCDの面積は?
*図は動画内参照
〇〇を作って解こう 吉祥女子中

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{3}{13} + \frac{8}{19} + \frac{3}{22} + \frac{1}{33} + \frac{3}{38} +\frac{4}{39}$
吉祥寺女子中学校
この動画を見る
$\frac{3}{13} + \frac{8}{19} + \frac{3}{22} + \frac{1}{33} + \frac{3}{38} +\frac{4}{39}$
吉祥寺女子中学校
あります!鬼難しい難問をスルリと解ける裏技!複雑な問題ほど威力を発揮するその方法とは!?【中学受験算数】【入試問題】【開智中学校】
単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
こばちゃん塾
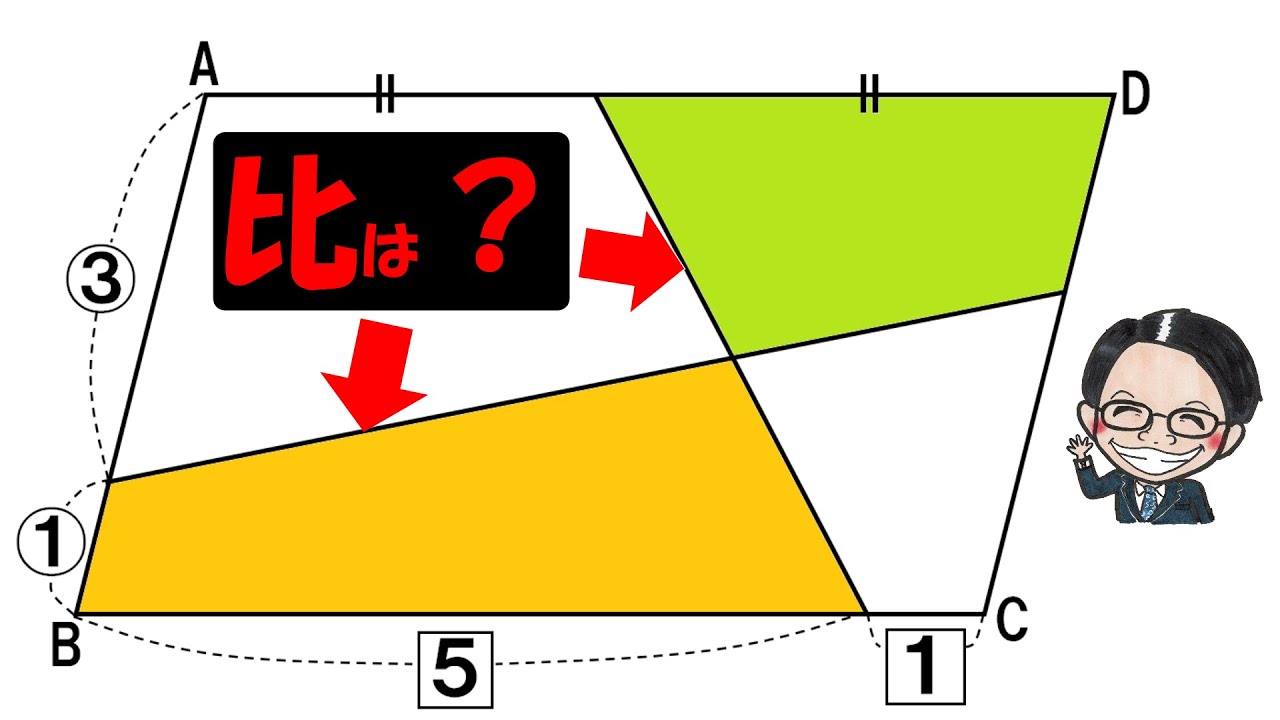
問題文全文(内容文):
2021春日部共栄中学校
三角形ABCが12㎠、三角形FDEが3㎠のとき、BFとFDの長さの比は?
2021帝京大学中学校
図のような三角形で、(1)~(3)に答えよう。
(1)三角形CDFの面積は三角形ABCの面積の何倍?
(2)BHとHFの長さの比は?
(3)三角形GHIの面積は三角形ABCの面積の何倍?
2021開智中学校
図の平行四辺形ABCDで(1)~(3)に答えよう
(1)QOとOSの長さの比は?
(2)CSとSDの長さの比は?
(3)四角形QBROと四角形POSDの面積比は?
*図は動画内参照
この動画を見る
2021春日部共栄中学校
三角形ABCが12㎠、三角形FDEが3㎠のとき、BFとFDの長さの比は?
2021帝京大学中学校
図のような三角形で、(1)~(3)に答えよう。
(1)三角形CDFの面積は三角形ABCの面積の何倍?
(2)BHとHFの長さの比は?
(3)三角形GHIの面積は三角形ABCの面積の何倍?
2021開智中学校
図の平行四辺形ABCDで(1)~(3)に答えよう
(1)QOとOSの長さの比は?
(2)CSとSDの長さの比は?
(3)四角形QBROと四角形POSDの面積比は?
*図は動画内参照
9.99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999

【受験算数】数の性質:海城過去問~積と最大公約数から整数を求める!【予習シリーズ算数・小5上】

単元:
#算数(中学受験)#計算と数の性質#数の性質その他#過去問解説(学校別)#海城中学
教材:
#予習シ#予習シ算数・小5上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
2けたの整数が2つあります。この2つの整数の積は4080,最大公約数は4です。この2つの整数を求めなさい。
この動画を見る
2けたの整数が2つあります。この2つの整数の積は4080,最大公約数は4です。この2つの整数を求めなさい。
こんなに飲めない...

単元:
#算数(中学受験)#文章題#文章題その他
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
ジュースの空き缶5本集めると、新品のジュース1本と交換してもらえる。
あなたは新品のジュースを200本もっている。
何本のジュースが飲めますか?
この動画を見る
ジュースの空き缶5本集めると、新品のジュース1本と交換してもらえる。
あなたは新品のジュースを200本もっている。
何本のジュースが飲めますか?
【受験算数】海城過去問~正六角形と正三角形の面積を比べる

単元:
#算数(中学受験)#過去問解説(学校別)#平面図形#相似と相似を利用した問題#海城中学
指導講師:
理数個別チャンネル
問題文全文(内容文):
周の長さが6㎝の正六角形の面積は、周の長さが6㎝の正三角形の面積の何倍ですか。
この動画を見る
周の長さが6㎝の正六角形の面積は、周の長さが6㎝の正三角形の面積の何倍ですか。
なんでか分かる?

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$7 \times 11 \times 13 $…の計算の謎紹介動画です
この動画を見る
$7 \times 11 \times 13 $…の計算の謎紹介動画です
【受験算数】規則性:数列を考えよう【予習シリーズ算数・小6上】

単元:
#算数(中学受験)#計算と数の性質#規則性(周期算・方陣算・数列・日暦算・N進法)
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
122334455....と続く数列の100番目の数は何でしょうか?【予習シリーズ 6年生】【数と規則性】
この動画を見る
122334455....と続く数列の100番目の数は何でしょうか?【予習シリーズ 6年生】【数と規則性】
