 大学入試解答速報
大学入試解答速報
 大学入試解答速報
大学入試解答速報
オススメの海外英語系YouTuber

単元:
#英語(中学生)#中1英語#中2英語#中3英語#英語リスニング・スピーキング#高校入試過去問(英語)#リスニング#英語
指導講師:
Morite2 English Channel
問題文全文(内容文):
この動画が提起する主要な問題点は、英語学習者が楽しく効果的に学べる海外のYouTubeチャンネルを見つけることの難しさです。
・特に、イギリス英語またはアメリカ英語のどちらを学びたいかによって、適切な学習リソースの選択に迷うことがあります。
・また、初心者から中級者まで、レベルに合わせた分かりやすい説明と綺麗な発音**を提供する信頼できるYouTuberの需要が高いです。
・この動画は、そのような学習者のニーズに応えるため、「英語学習が楽しくなる海外YouTuberを教えてほしい」という具体的な疑問に答える形で情報を提供しています。
・したがって、動画の目的は、学習者が自分に合った質の高い英語学習チャンネルを効率的に見つける手助けをすることにあります。
・紹介されているルーシーとレイチェルのチャンネルは、この「見つけにくい」という問題を解決するための具体的な選択肢として提示されています。
この動画を見る
この動画が提起する主要な問題点は、英語学習者が楽しく効果的に学べる海外のYouTubeチャンネルを見つけることの難しさです。
・特に、イギリス英語またはアメリカ英語のどちらを学びたいかによって、適切な学習リソースの選択に迷うことがあります。
・また、初心者から中級者まで、レベルに合わせた分かりやすい説明と綺麗な発音**を提供する信頼できるYouTuberの需要が高いです。
・この動画は、そのような学習者のニーズに応えるため、「英語学習が楽しくなる海外YouTuberを教えてほしい」という具体的な疑問に答える形で情報を提供しています。
・したがって、動画の目的は、学習者が自分に合った質の高い英語学習チャンネルを効率的に見つける手助けをすることにあります。
・紹介されているルーシーとレイチェルのチャンネルは、この「見つけにくい」という問題を解決するための具体的な選択肢として提示されています。
藤川天の第2回全統共通テスト模試自己採点結果公開

単元:
#大学入試解答速報#英語#共通テスト
指導講師:
Morite2 English Channel
問題文全文(内容文):
藤川天の第2回共通テスト自己採点
・地理B 34点
・国語 60点
・英語 R43点 L44点
・数学 1A 21点 2B 27点
・物理 34点
・化学 38点
・情報 45点
この動画を見る
藤川天の第2回共通テスト自己採点
・地理B 34点
・国語 60点
・英語 R43点 L44点
・数学 1A 21点 2B 27点
・物理 34点
・化学 38点
・情報 45点
2024追試第3問 問2 沈殿生成反応

単元:
#化学#無機#イオンの反応と分離#理科(高校生)#化学#共通テスト
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
表1のA欄に示す2種類の金属イオンを含む水溶液㋐〜㋒がある。
一方の金属イオンを沈殿として得たい。
このとき、B欄の操作では一方の金属イオンのみを沈殿させることができない水溶液は㋐〜㋒のどれか。
すべてを正しく選 んでいるものを、後の①~⑥のうちから一つ選べ。
ただし、金属イオンはそれ ぞれの硝酸塩を水に溶かしたものとする。
水溶液㋐
銀イオン:$\ce{Pb^{2+}},\ce{Fe^{2+}}$
操作:水溶液に塩酸を加えて沈殿を得る。
水溶液㋑
銀イオン:$\ce{Fe^{3+}},\ce{Zn^{2+}}$
操作:過剰のアンモニアを加えて沈殿を得る。
水溶液㋒
銀イオン:$\ce{Ca^{2+}},\ce{Ba^{2+}}$
操作:水溶液にアンモニアを加え弱塩基性としてから、
炭酸アンモニウムを加えて沈殿を得る。
※表は動画内参照
この動画を見る
表1のA欄に示す2種類の金属イオンを含む水溶液㋐〜㋒がある。
一方の金属イオンを沈殿として得たい。
このとき、B欄の操作では一方の金属イオンのみを沈殿させることができない水溶液は㋐〜㋒のどれか。
すべてを正しく選 んでいるものを、後の①~⑥のうちから一つ選べ。
ただし、金属イオンはそれ ぞれの硝酸塩を水に溶かしたものとする。
水溶液㋐
銀イオン:$\ce{Pb^{2+}},\ce{Fe^{2+}}$
操作:水溶液に塩酸を加えて沈殿を得る。
水溶液㋑
銀イオン:$\ce{Fe^{3+}},\ce{Zn^{2+}}$
操作:過剰のアンモニアを加えて沈殿を得る。
水溶液㋒
銀イオン:$\ce{Ca^{2+}},\ce{Ba^{2+}}$
操作:水溶液にアンモニアを加え弱塩基性としてから、
炭酸アンモニウムを加えて沈殿を得る。
※表は動画内参照
2024追試第3問 問1 14族元素の性質

単元:
#化学#無機#非金属元素の単体と化合物#理科(高校生)#化学#共通テスト
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
14族の元素性質
元素ア~エは炭素C、ケイ素$\ce{Si}$,スズ$\ce{Sn}$, 鉛$\ce{Pb}$ のいずれかであり、次の 記述Ⅰ~Ⅲに示す性質や特徴をもつ。
㋐〜㋓に当てはまる元素の組合せとして 最も適当なものを、後の①~⑧のうちから一つ選べ。
Ⅰ ㋐と㋑の単体は、希硝酸にも水酸化ナトリウム水溶液にも溶解する。
Ⅱ ㋐を含むガラスは、光の屈折率が大きく、透明なガラスや光学レンズに用 いられる。
Ⅲ㋒の酸化物をエの単体で還元することでウの単体が製造される。
※表は動画内参照
この動画を見る
14族の元素性質
元素ア~エは炭素C、ケイ素$\ce{Si}$,スズ$\ce{Sn}$, 鉛$\ce{Pb}$ のいずれかであり、次の 記述Ⅰ~Ⅲに示す性質や特徴をもつ。
㋐〜㋓に当てはまる元素の組合せとして 最も適当なものを、後の①~⑧のうちから一つ選べ。
Ⅰ ㋐と㋑の単体は、希硝酸にも水酸化ナトリウム水溶液にも溶解する。
Ⅱ ㋐を含むガラスは、光の屈折率が大きく、透明なガラスや光学レンズに用 いられる。
Ⅲ㋒の酸化物をエの単体で還元することでウの単体が製造される。
※表は動画内参照
気づいた?
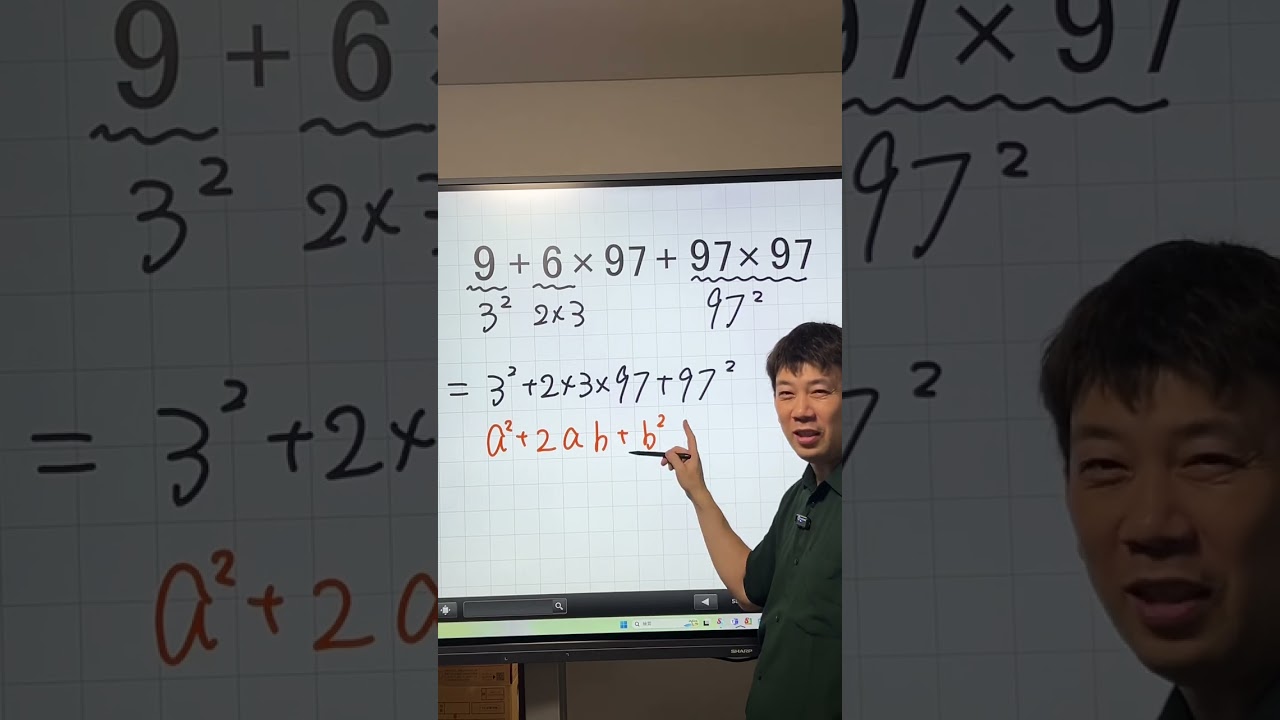
視聴者の僚太さんの難易度高めの積分です。大事な感覚が盛り込まれてます。

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#大学入試解答速報
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x^2}{(1+x^2)\sqrt{ 1+x^2 }}$
この動画を見る
$\displaystyle \int \displaystyle \frac{x^2}{(1+x^2)\sqrt{ 1+x^2 }}$
【2時間半で完成関係詞】関係代名詞・関係副詞【基礎英文法講座総集編⑤】

単元:
#英語(高校生)#英文法#関係代名詞・関係副詞・複合関係詞#英語
指導講師:
Morite2 English Channel
問題文全文(内容文):
空所に入るのは?
The time might come ( ) global warming can be solved.
1. which
2. when
3. who
4. what
この動画を見る
空所に入るのは?
The time might come ( ) global warming can be solved.
1. which
2. when
3. who
4. what
【新課程対応】共通テスト(旧センター試験)過去問解説 化学 2017年追試 第2問 問2 活性化エネルギー
単元:
#化学#化学理論#化学反応の速さ#理科(高校生)#大学入試解答速報#化学#共通テスト
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
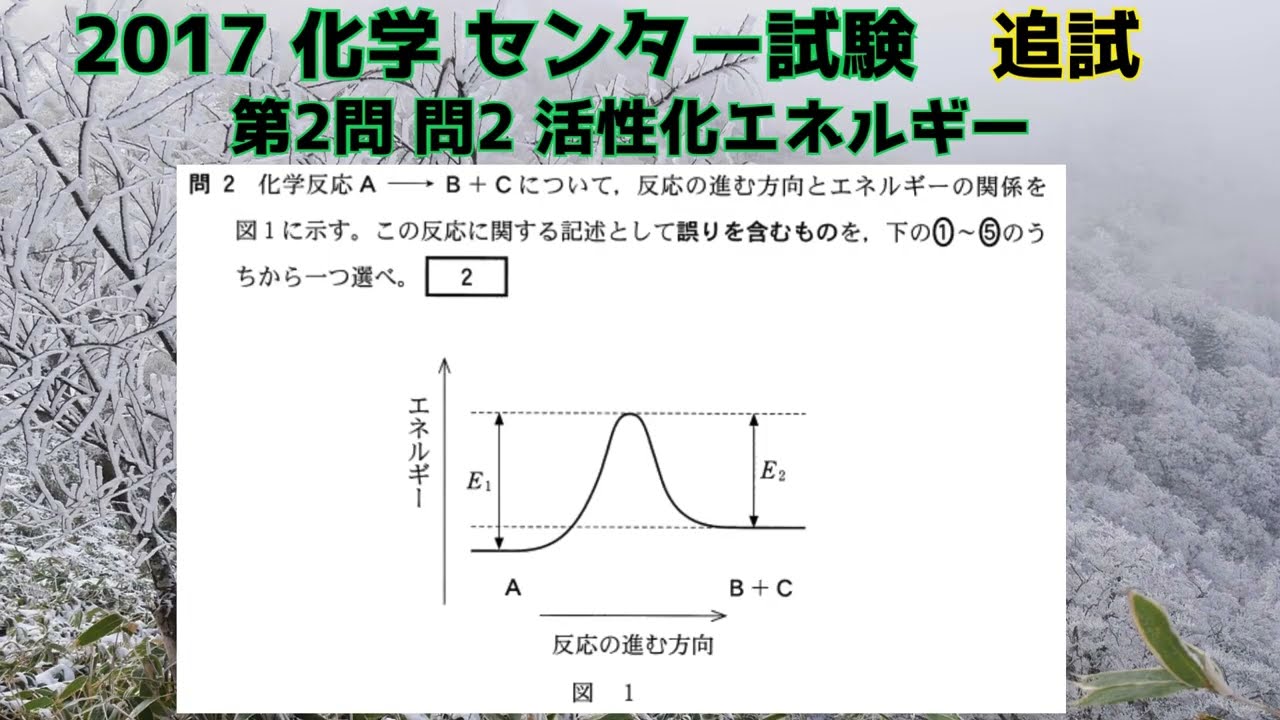
化学反応$A→ B+C$について、反応の進む方向とエネルギーの関係を図1に示す。
この反応に関する記述として誤りを含むものを、下の①~⑤のう ちから一つ選べ。
① この反応は吸熱反応である。
② この反応が進むときに経るエネルギーの高い状態を、($▬$還移状態)という。
③ この反応の活性化エネルギーは$E_2$である。
④ 触媒を用いると、反応経路が変わり、活性化エネルギーを小さくできる。
⑤ 触媒を用いても$▬$は変わらない。
(反応エンタルピー)
※グラフは動画内参照
この動画を見る
化学反応$A→ B+C$について、反応の進む方向とエネルギーの関係を図1に示す。
この反応に関する記述として誤りを含むものを、下の①~⑤のう ちから一つ選べ。
① この反応は吸熱反応である。
② この反応が進むときに経るエネルギーの高い状態を、($▬$還移状態)という。
③ この反応の活性化エネルギーは$E_2$である。
④ 触媒を用いると、反応経路が変わり、活性化エネルギーを小さくできる。
⑤ 触媒を用いても$▬$は変わらない。
(反応エンタルピー)
※グラフは動画内参照
言語アキネーター【バイエルン・オーストリア語】 #shorts

速報最終日は17:00~18:30です!前半60分【早大商・社会科学部への最終戦略】+後半30分【国公立2次:論述の得点の稼ぎ方】)…動画配信後に解析を yukiobible.com にUPします!

単元:
#世界史#大学入試過去問・共通テスト・模試関連#大学入試解答速報#早慶
指導講師:
世界史予備校講師佐藤幸夫 Yukio Sato チャンネル
問題文全文(内容文):
速報最終日は17:00~18:30です!
「前半60分【早大商・社会科学部への最終戦略】+後半30分【国公立2次:論述の得点の稼ぎ方】」について解説している動画です。
この動画を見る
速報最終日は17:00~18:30です!
「前半60分【早大商・社会科学部への最終戦略】+後半30分【国公立2次:論述の得点の稼ぎ方】」について解説している動画です。
毎年恒例【早慶即日速報プラスα】は2/18の世界史のみ(早稲田文と人科:全問生解説&教育学部への最終戦略も考えます!)…動画配信後に解析を yukiobible.com にUPします!

単元:
#世界史#大学入試過去問・共通テスト・模試関連#大学入試解答速報#早慶
指導講師:
世界史予備校講師佐藤幸夫 Yukio Sato チャンネル
問題文全文(内容文):
毎年恒例【早慶即日速報プラスα】は2/18の世界史のみ
「早稲田文と人科:全問生解説&教育学部への最終戦略」について解説しています。
この動画を見る
毎年恒例【早慶即日速報プラスα】は2/18の世界史のみ
「早稲田文と人科:全問生解説&教育学部への最終戦略」について解説しています。
毎年恒例【早慶即日速報プラスα】は2/16の世界史(慶應法:全問生解説・早稲田選択文の必殺解説)・日本史(早稲田法・慶應文)…完璧解説!動画配信後に解析をyukiobible.comにUPします!

単元:
#日本史#世界史#大学入試過去問・共通テスト・模試関連#大学入試解答速報#早慶
指導講師:
世界史予備校講師佐藤幸夫 Yukio Sato チャンネル
問題文全文(内容文):
毎年恒例【早慶即日速報プラスα】
「世界史(慶應法:全問生解説・早稲田選択文の必殺解説)・日本史(早稲田法・慶應文)」について解説しています。
この動画を見る
毎年恒例【早慶即日速報プラスα】
「世界史(慶應法:全問生解説・早稲田選択文の必殺解説)・日本史(早稲田法・慶應文)」について解説しています。
毎年恒例【早慶即日速報プラスα】は2/15の世界史(慶應文:全問生解説・早稲田法など)・日本史(慶應商学部)…明日以降への問題を完璧解説!動画配信後に解析をyukiobible.comにUPします!

単元:
#日本史#世界史#大学入試過去問・共通テスト・模試関連#大学入試解答速報#早慶
指導講師:
世界史予備校講師佐藤幸夫 Yukio Sato チャンネル
問題文全文(内容文):
毎年恒例【早慶即日速報プラスα】
「世界史(慶應文:全問生解説・早稲田法など)・日本史(慶應商学部)」について解説しています。
この動画を見る
毎年恒例【早慶即日速報プラスα】
「世界史(慶應文:全問生解説・早稲田法など)・日本史(慶應商学部)」について解説しています。
毎年恒例【早慶即日速報プラスα】は2/14は世界史(慶應商:全問生解説・明治法・青学文)・日本史(慶應経済)…明日以降への問題を完璧解説!動画配信後に解析をyukiobible.comにUPします!

単元:
#日本史#世界史#大学入試解答速報#早慶#GMARCH
指導講師:
世界史予備校講師佐藤幸夫 Yukio Sato チャンネル
問題文全文(内容文):
毎年恒例【早慶即日速報プラスα】
「世界史(慶應商:全問生解説・明治法・青学文)・日本史(慶應経済)」について解説しています。
この動画を見る
毎年恒例【早慶即日速報プラスα】
「世界史(慶應商:全問生解説・明治法・青学文)・日本史(慶應経済)」について解説しています。
毎年恒例【早慶即日速報プラスα】は2/13は世界史(明治文+慶應経済:全問生解説)・日本史(早大文化構想学部)…明日以降への問題を完璧解説!動画配信後に解析をyukiobible.comにUPします!

単元:
#世界史#大学入試過去問・共通テスト・模試関連#大学入試解答速報#早慶
指導講師:
世界史予備校講師佐藤幸夫 Yukio Sato チャンネル
問題文全文(内容文):
毎年恒例【早慶即日速報プラスα】
「世界史(明治文+慶應経済:全問生解説)・日本史(早大文化構想学部)」について解説しています。
この動画を見る
毎年恒例【早慶即日速報プラスα】
「世界史(明治文+慶應経済:全問生解説)・日本史(早大文化構想学部)」について解説しています。
毎年恒例【早慶即日速報プラスα】は2月12日は世界史〈早稲田文講の完全解説+慶應への一言+MARCH一部〉の解析…明日以降への問題を完璧解説!動画中の解答訂正あり〈注意〉

単元:
#世界史#大学入試過去問・共通テスト・模試関連#大学入試解答速報#早慶#GMARCH
指導講師:
世界史予備校講師佐藤幸夫 Yukio Sato チャンネル
問題文全文(内容文):
毎年恒例【早慶即日速報プラスα】
「世界史〈早稲田文講の完全解説+慶應への一言+MARCH一部〉」の解析です。
この動画を見る
毎年恒例【早慶即日速報プラスα】
「世界史〈早稲田文講の完全解説+慶應への一言+MARCH一部〉」の解析です。
毎年恒例【MARCH即日速報プラスα】は2月11日は世界史のみ〈早稲田の明日への早稲語&早稲文の30分レッスン+明治・法政・中央〉の解析…新しい問題を解説!問題・解析はyukiobible.comより

単元:
#世界史#大学入試過去問・共通テスト・模試関連#大学入試解答速報#早慶#GMARCH
指導講師:
世界史予備校講師佐藤幸夫 Yukio Sato チャンネル
問題文全文(内容文):
毎年恒例【MARCH即日速報プラスα】は2月11日は世界史のみ
「早稲田の明日への早稲語&早稲文の30分レッスン+明治・法政・中央」の解析です。
この動画を見る
毎年恒例【MARCH即日速報プラスα】は2月11日は世界史のみ
「早稲田の明日への早稲語&早稲文の30分レッスン+明治・法政・中央」の解析です。
毎年恒例【MARCH即日速報】は2月10日は〈明治・法政・中央・青学・学習院の世界史〉の解析…代ゼミ講師がまだまだ出題される新しい問題を解説!知識の再確認!問題・解析はyukiobible.comより

単元:
#世界史#大学入試過去問・共通テスト・模試関連#大学入試解答速報#GMARCH
指導講師:
世界史予備校講師佐藤幸夫 Yukio Sato チャンネル
問題文全文(内容文):
毎年恒例【MARCH即日速報】
「明治・法政・中央・青学・学習院の世界史」についての解析です。
この動画を見る
毎年恒例【MARCH即日速報】
「明治・法政・中央・青学・学習院の世界史」についての解析です。
【化学】古い過去問 センター試験2003年度 第5問 問6 アルコール分子中のC=Cの数を決定しよう

単元:
#化学#有機#酸素を含む脂肪族化合物#理科(高校生)#大学入試解答速報#化学#共通テスト
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
示性式 $C_mH_nOH$で表される1価の鎖式不飽和アルコール
(三重結合を含まない)$42g$をナトリウムと完全に反応させたところ、
水素 $0.25mol$が発生した。
このアルコール$21g$に、触媒の存在下で水素を付加させたところ、すべてが飽和に変化した。
このとき消費された水素は標準状態で何$l$か。
最も適当な数値を、次の①~⑥のうちから一つ選べ。
①$2.8$
②$5.6$
③$11$
④$22$
⑤$34$
⑥$45$
この動画を見る
示性式 $C_mH_nOH$で表される1価の鎖式不飽和アルコール
(三重結合を含まない)$42g$をナトリウムと完全に反応させたところ、
水素 $0.25mol$が発生した。
このアルコール$21g$に、触媒の存在下で水素を付加させたところ、すべてが飽和に変化した。
このとき消費された水素は標準状態で何$l$か。
最も適当な数値を、次の①~⑥のうちから一つ選べ。
①$2.8$
②$5.6$
③$11$
④$22$
⑤$34$
⑥$45$
毎年恒例【MARCH&同志社即日速報】は2月8日は〈同志社・明治・法政・立教・青学の世界史&日本史〉の解析…代ゼミ講師が激励!問題・解析はyukiobible.comより

単元:
#日本史#世界史#大学入試過去問・共通テスト・模試関連#大学入試解答速報#GMARCH#関関同立
指導講師:
世界史予備校講師佐藤幸夫 Yukio Sato チャンネル
問題文全文(内容文):
毎年恒例【MARCH&同志社即日速報】
「同志社・明治・法政・立教・青学の世界史&日本史」について解析しています。
この動画を見る
毎年恒例【MARCH&同志社即日速報】
「同志社・明治・法政・立教・青学の世界史&日本史」について解析しています。
2024年度 共通テスト解説 化学 第5問 問3 質量分析法-クロロメタンの質量スペクトル

単元:
#化学#化学基礎1ー物質の構成#理科(高校生)#大学入試解答速報#化学#共通テスト
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
a:塩素$CI$には2種の同位体$^{36}CI$と$^{37}CI$があり、それらは天然におよそ$3:1$の割合で存在する。
図3と同じエネルギーでクロロメタン$CH_3CI$をイオン化した場合の、相対質量が$50$付近の質量スペクトルはどれか。
最も適当なものを、次の①~⑥のうちから一つ選べ。
ただし、$^{36}CI$と$^{37}CI$の対質量は、それぞれ$35$と$37$とする。
※図は動画内参照
この動画を見る
a:塩素$CI$には2種の同位体$^{36}CI$と$^{37}CI$があり、それらは天然におよそ$3:1$の割合で存在する。
図3と同じエネルギーでクロロメタン$CH_3CI$をイオン化した場合の、相対質量が$50$付近の質量スペクトルはどれか。
最も適当なものを、次の①~⑥のうちから一つ選べ。
ただし、$^{36}CI$と$^{37}CI$の対質量は、それぞれ$35$と$37$とする。
※図は動画内参照
共通テスト(旧センター試験)過去問解説 化学 2017年追試 第1問 問1 電子の総数

単元:
#化学#化学基礎1ー物質の構成#理科(高校生)#大学入試解答速報#化学#共通テスト
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
イオンとその生成に関する記述として誤りを含むものを、
次の①~⑤のうちから一つ選べ。
① イオン化エネルギー(第一イオン化エネルギー)が
小さい原子は陽イオンになりやすい。
② 電子親和力が大きい原子は陰イオンになりやすい。
③ 17族元素の原子は同一周期の他の元素の原子と比較して、
陰イオンになりやすい。
④ 18族元素の原子は同一周期の中でイオン化エネルギー
(第一イオン化エネルギー)が最も大きい。
⑤ 2族元素の原子の2価の陽イオンは、
同一周期の希(貴)ガスと同じ電子配置である。
この動画を見る
イオンとその生成に関する記述として誤りを含むものを、
次の①~⑤のうちから一つ選べ。
① イオン化エネルギー(第一イオン化エネルギー)が
小さい原子は陽イオンになりやすい。
② 電子親和力が大きい原子は陰イオンになりやすい。
③ 17族元素の原子は同一周期の他の元素の原子と比較して、
陰イオンになりやすい。
④ 18族元素の原子は同一周期の中でイオン化エネルギー
(第一イオン化エネルギー)が最も大きい。
⑤ 2族元素の原子の2価の陽イオンは、
同一周期の希(貴)ガスと同じ電子配置である。
毎年恒例【同志社英語速報~どこよりも早い!即日速報】2月4・5日に行われた同志社大学の英語を代ゼミの同志社の英語担当講師が解析し、残りの戦略を伝授します!問題・解析はyukiobible.comより

単元:
#世界史#大学入試過去問・共通テスト・模試関連#大学入試解答速報#英語#関関同立
指導講師:
世界史予備校講師佐藤幸夫 Yukio Sato チャンネル
問題文全文(内容文):
毎年恒例【同志社英語速報~どこよりも早い!即日速報】
「同志社大学の英語を代ゼミの同志社の英語担当講師が解析し、残りの戦略を伝授」しています。
この動画を見る
毎年恒例【同志社英語速報~どこよりも早い!即日速報】
「同志社大学の英語を代ゼミの同志社の英語担当講師が解析し、残りの戦略を伝授」しています。
毎年恒例【関関同立&MARCH即日速報】は2月5日は〈関大・同志社の世界史&日本史〉&明治(全学部)の解析と立教前日アドバイス…代ゼミ講師が解析&激励!問題・解析はyukiobible.comより

単元:
#世界史#大学入試過去問・共通テスト・模試関連#大学入試解答速報#GMARCH#関関同立
指導講師:
世界史予備校講師佐藤幸夫 Yukio Sato チャンネル
問題文全文(内容文):
毎年恒例【関関同立&MARCH即日速報】
「関大・同志社の世界史&日本史&明治(全学部)の解析と立教前日アドバイス」をしています。
この動画を見る
毎年恒例【関関同立&MARCH即日速報】
「関大・同志社の世界史&日本史&明治(全学部)の解析と立教前日アドバイス」をしています。
毎年恒例【関関同立即日速報】は2月4日は〈関学・立命館の世界史〉と明日の明治&同志社へのワンポイントアドバイスもあり!問題・解析はyukiobible.comより

単元:
#世界史#大学入試過去問・共通テスト・模試関連#大学入試解答速報#関関同立
指導講師:
世界史予備校講師佐藤幸夫 Yukio Sato チャンネル
問題文全文(内容文):
毎年恒例【関関同立即日速報】は2月4日は
「関学・立命館の世界史の解析」と「明日の明治&同志社へのワンポイントアドバイス」です。
この動画を見る
毎年恒例【関関同立即日速報】は2月4日は
「関学・立命館の世界史の解析」と「明日の明治&同志社へのワンポイントアドバイス」です。
毎年恒例【関関同立即日速報】は2月3日は〈関大・関学・立命館の世界史&日本史〉→明日の入試に必ずつながる即日速報を代ゼミ講師が解析&翌日アドバイスをします!問題・解析はyukiobible.comより

単元:
#日本史#世界史#大学入試過去問・共通テスト・模試関連#大学入試解答速報#関関同立
指導講師:
世界史予備校講師佐藤幸夫 Yukio Sato チャンネル
問題文全文(内容文):
毎年恒例【関関同立即日速報】
「関大・関学・立命館の世界史&日本史」について、解析とアドバイスをしています。
この動画を見る
毎年恒例【関関同立即日速報】
「関大・関学・立命館の世界史&日本史」について、解析とアドバイスをしています。
【化学】古い過去問 センター試験2003年度 第3問 問2 気体の発生と反応の種類

単元:
#化学#化学基礎2ー物質の変化#化学変化と化学反応式#理科(高校生)#大学入試解答速報#化学#共通テスト
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
次の反応a~eにおいて、下線で示した化合物が
酸化剤としてはたらくものの組合せとして最も適当なものを、下の①~⑧のうちから一つ選べ。
a 銅に濃硫酸を加えて加熱すると、二酸化硫黄が発生する。
b 硫化鉄(Ⅱ)に希硫酸を加えると、硫化水素が発生する。
c 酸化マンガン(V)に濃塩酸を加えて加熱すると、塩素が発生する。
d 塩素酸カリウムに酸化マンガン(V)を加えて加熱すると、酸素が発生する。
e 過酸化水素水に硫化水素を吹き込むと、硫黄が生じる。
①$a・b $
②$a・c $
③$a・d $
④$a・e $
⑤$b・d $
⑥$b・e $
⑦$c・d $
⑧$c・e $
この動画を見る
次の反応a~eにおいて、下線で示した化合物が
酸化剤としてはたらくものの組合せとして最も適当なものを、下の①~⑧のうちから一つ選べ。
a 銅に濃硫酸を加えて加熱すると、二酸化硫黄が発生する。
b 硫化鉄(Ⅱ)に希硫酸を加えると、硫化水素が発生する。
c 酸化マンガン(V)に濃塩酸を加えて加熱すると、塩素が発生する。
d 塩素酸カリウムに酸化マンガン(V)を加えて加熱すると、酸素が発生する。
e 過酸化水素水に硫化水素を吹き込むと、硫黄が生じる。
①$a・b $
②$a・c $
③$a・d $
④$a・e $
⑤$b・d $
⑥$b・e $
⑦$c・d $
⑧$c・e $
毎年恒例【関関同立即日速報】は2月2日は〈関大・関学・立命館の世界史&日本史〉→明日の入試に必ずつながる即日速報を代ゼミ講師が解析&翌日アドバイスをします!問題・解析はyukiobible.comより

単元:
#日本史#世界史#大学入試過去問・共通テスト・模試関連#大学入試解答速報#関関同立
指導講師:
世界史予備校講師佐藤幸夫 Yukio Sato チャンネル
問題文全文(内容文):
毎年恒例【関関同立即日速報】
「関大・関学・立命館の世界史&日本史」の解析とアドバイスです。
この動画を見る
毎年恒例【関関同立即日速報】
「関大・関学・立命館の世界史&日本史」の解析とアドバイスです。
毎年恒例【関関同立即日速報】は2月1日は〈関大・関学・立命館の世界史&英語〉→明日の入試に必ずつながる即日速報を代ゼミ講師が解析&翌日アドバイスをします!今日を知ることは必ず明日につながります!

単元:
#世界史#大学入試過去問・共通テスト・模試関連#大学入試解答速報#関関同立
指導講師:
世界史予備校講師佐藤幸夫 Yukio Sato チャンネル
問題文全文(内容文):
毎年恒例【関関同立即日速報】
「関大・関学・立命館の世界史&英語」の解析とアドバイスです。
この動画を見る
毎年恒例【関関同立即日速報】
「関大・関学・立命館の世界史&英語」の解析とアドバイスです。
共通テスト(旧センター試験)過去問解説 化学 2016年追試 第7問 問2 糖の構造
単元:
#化学#大学入試過去問(化学)#共通テスト#化学(高分子)#糖類#理科(高校生)#大学入試解答速報
指導講師:
ぺんぎん高校化学問題集
問題文全文(内容文):
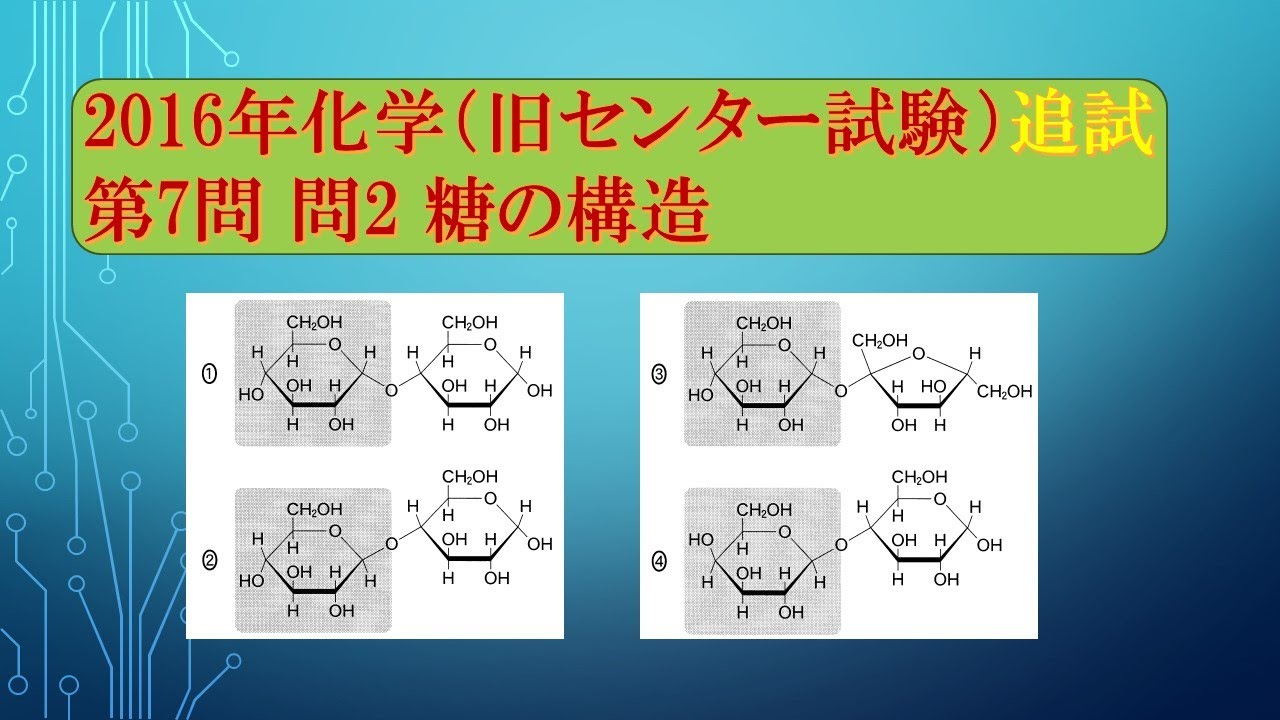
次の記述(a・b)の両方に当てはまる化合物を、
下の①~④のうちから一つ選べ。
a 左側の単糖部分(灰色部分)が$a^-$
コーグルコース構造($a^-$グルコース単位)であるもの。
b 水溶液にアンモニア性硝酸銀水溶液を加えて温めると、
銀が析出するもの。
※図は動画内参照
この動画を見る
次の記述(a・b)の両方に当てはまる化合物を、
下の①~④のうちから一つ選べ。
a 左側の単糖部分(灰色部分)が$a^-$
コーグルコース構造($a^-$グルコース単位)であるもの。
b 水溶液にアンモニア性硝酸銀水溶液を加えて温めると、
銀が析出するもの。
※図は動画内参照
