鹿児島大学
鹿児島大学
【高校数学】毎日積分58日目~47都道府県制覇への道~【②鹿児島】【毎日17時投稿】
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#鹿児島大学#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$x＞0$で定義された曲線
$C : y=(log x)^2$
を考える
(1)$a$を正の実数とする時、点$P(a,(log a)^2)$における曲線$C$の接線$L$の方程式を求めよ。
(2)$a＞1$のとき、接線$L$と$x$軸の交点の$x$座標が最大となる場合の$a$の値$a_0$を求めよ。
(3)$a$の値が(2)の$a_0$に等しいとき、直線$L$の$y≧0$の部分と曲線$C$と$x$軸で囲まれた部分を、$x$軸の周りに1回転させてできる図形の体積を求めよ。
【鹿児島大学 2023】
この動画を見る
$x＞0$で定義された曲線
$C : y=(log x)^2$
を考える
(1)$a$を正の実数とする時、点$P(a,(log a)^2)$における曲線$C$の接線$L$の方程式を求めよ。
(2)$a＞1$のとき、接線$L$と$x$軸の交点の$x$座標が最大となる場合の$a$の値$a_0$を求めよ。
(3)$a$の値が(2)の$a_0$に等しいとき、直線$L$の$y≧0$の部分と曲線$C$と$x$軸で囲まれた部分を、$x$軸の周りに1回転させてできる図形の体積を求めよ。
【鹿児島大学 2023】
鹿児島大（医）連立漸化式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#鹿児島大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a_1=2,b_1=1$
$a_{n+1}=2a_n+3b_n-2$
$b_{n+1}=a_n+4b_n+2$
一般項$a_n$を求めよ
出典：2017年鹿児島大学医学部 過去問
この動画を見る
$a_1=2,b_1=1$
$a_{n+1}=2a_n+3b_n-2$
$b_{n+1}=a_n+4b_n+2$
一般項$a_n$を求めよ
出典：2017年鹿児島大学医学部 過去問
鹿児島大 漸化式
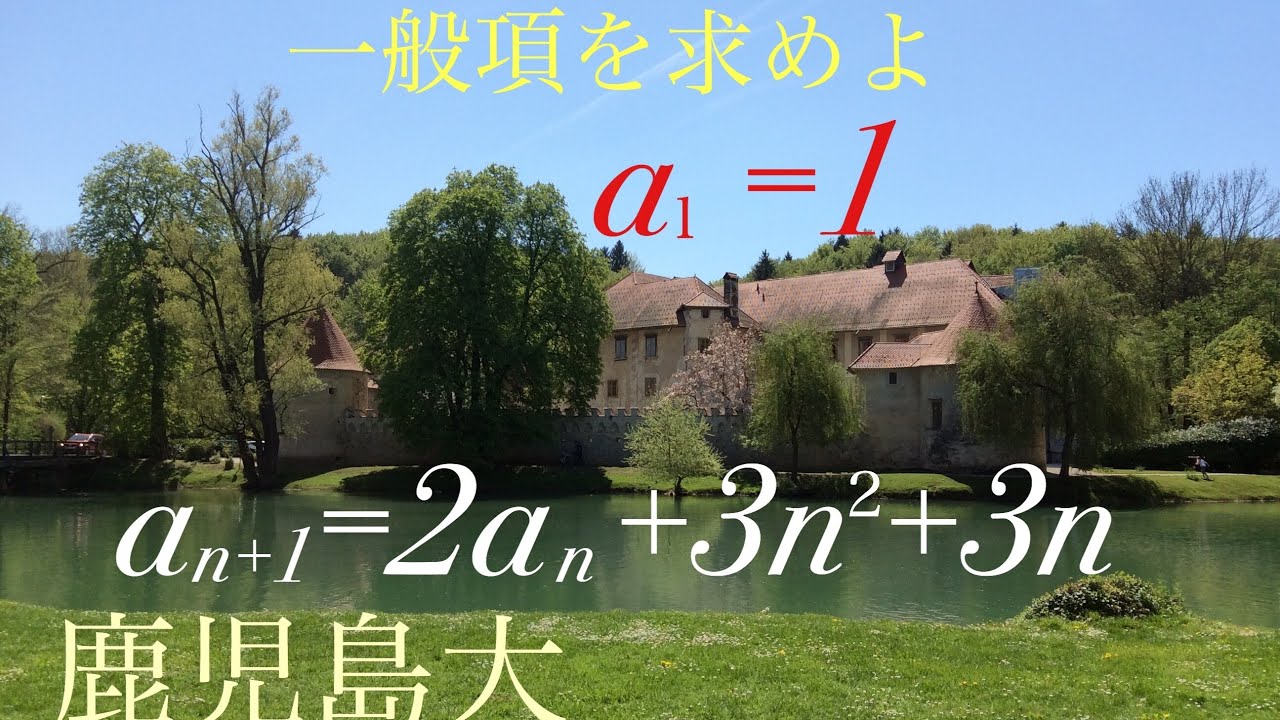
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#鹿児島大学#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a_1=1$ 一般項を求めよ
$a_{n+1}=2a_n+3n^2+3n$
出典：2019年鹿児島大学 過去問
この動画を見る
$a_1=1$ 一般項を求めよ
$a_{n+1}=2a_n+3n^2+3n$
出典：2019年鹿児島大学 過去問
鹿児島大（医他）数列の和 高校数学 Mathematics Japanese university entrance exam
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#数学(高校生)#鹿児島大学#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\sum_{k=1}^{n} \displaystyle \frac{2k-1}{2^k}$
出典：鹿児島大学 過去問
この動画を見る
$\sum_{k=1}^{n} \displaystyle \frac{2k-1}{2^k}$
出典：鹿児島大学 過去問
鹿児島（医）慶應（理） 高校数学 Japanese university entrance exam questions
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#複素数平面#集合と命題（集合・命題と条件・背理法）#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#鹿児島大学#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
鹿児島大学過去問題・類慶応義塾大学
二つの整数の平方の和で表される数
全体からなる集合をA
・x,yが集合Aの要素であるとき、積xyも集合Aの要素であることを証明せよ
・5および$5^5$は集合Aの要素であることを示せ
この動画を見る
鹿児島大学過去問題・類慶応義塾大学
二つの整数の平方の和で表される数
全体からなる集合をA
・x,yが集合Aの要素であるとき、積xyも集合Aの要素であることを証明せよ
・5および$5^5$は集合Aの要素であることを示せ