 茨城大学
茨城大学
 茨城大学
茨城大学
#茨城大学2024#定積分_11#元高校教員
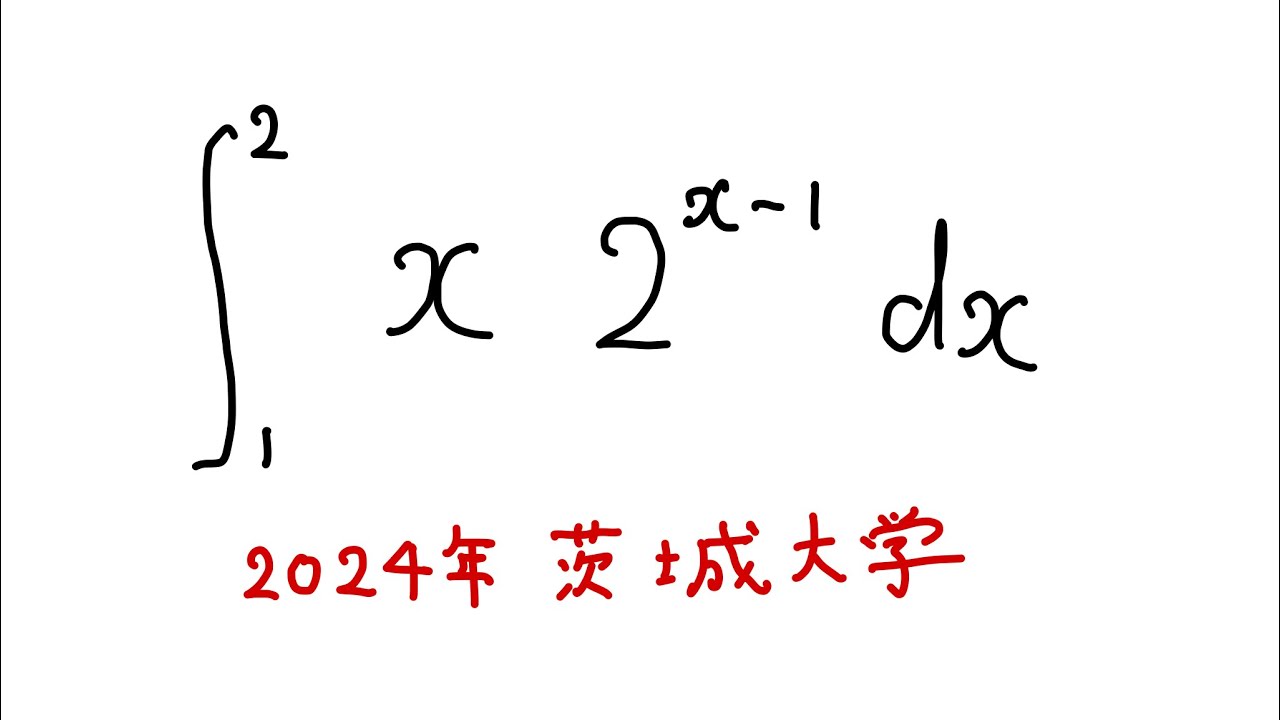
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2} x 2^{x-1}$ $dx$
出典:2024年茨城大学
この動画を見る
$\displaystyle \int_{1}^{2} x 2^{x-1}$ $dx$
出典:2024年茨城大学
#茨城大学2024#定積分_8#元高校教員

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \cos\theta\sin 2 \theta d \theta$
出典:2024年茨城大学後期
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \cos\theta\sin 2 \theta d \theta$
出典:2024年茨城大学後期
#茨城大学2024#定積分_7#元高校教員

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} e^x(e^{2x}+\frac{1}{e^{2x}}) dx$
出典:2024年茨城大学
この動画を見る
$\displaystyle \int_{0}^{1} e^x(e^{2x}+\frac{1}{e^{2x}}) dx$
出典:2024年茨城大学
#茨城大学後期2024#定積分_6#元高校教員

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{2}^{4} \displaystyle \frac{2}{x^2-1} dx$
出典:2024年茨城大学後期
この動画を見る
$\displaystyle \int_{2}^{4} \displaystyle \frac{2}{x^2-1} dx$
出典:2024年茨城大学後期
#茨城大学2024#区分求積法_5#元高校教員

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n^{3}}\displaystyle \sum_{k=1}^n (n-k)^2$
出典:2024年茨城大学
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n^{3}}\displaystyle \sum_{k=1}^n (n-k)^2$
出典:2024年茨城大学
#茨城大学2024#定積分_2#元高校教員
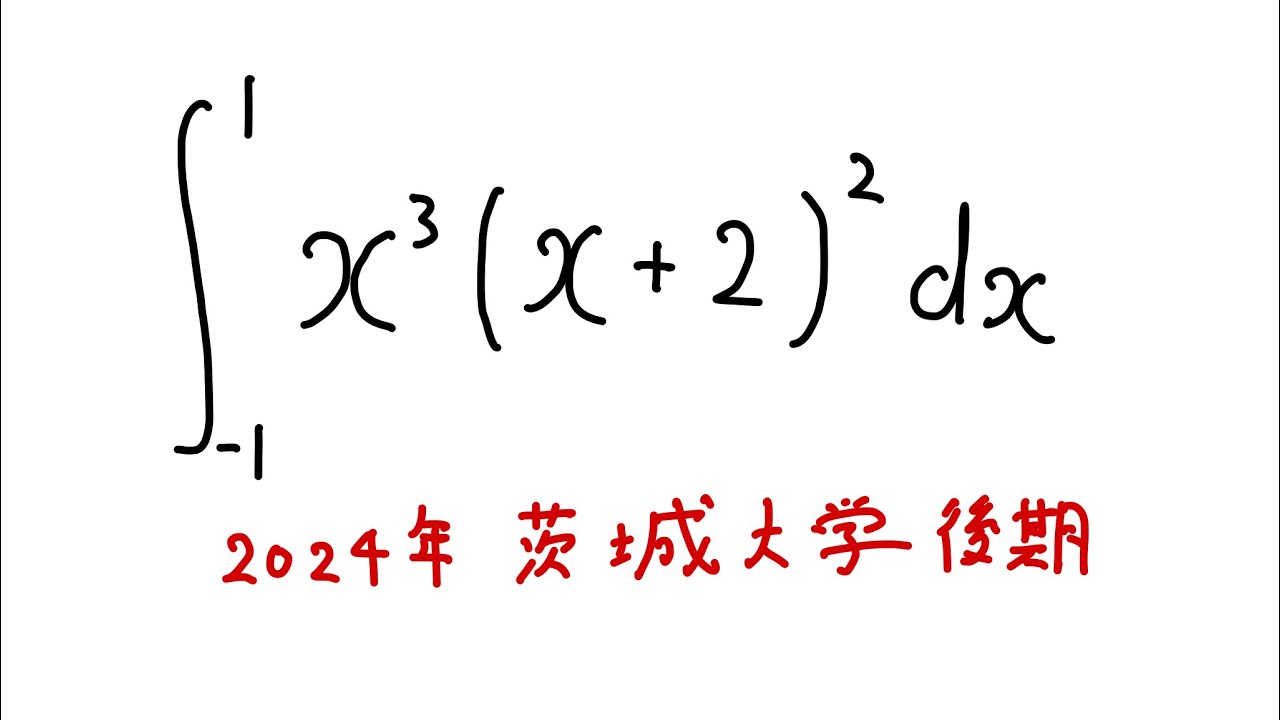
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1} x^3(x+2)^2 dx$
出典:2024年茨城大学後期
この動画を見る
$\displaystyle \int_{-1}^{1} x^3(x+2)^2 dx$
出典:2024年茨城大学後期
#茨城大学2024_1#定積分
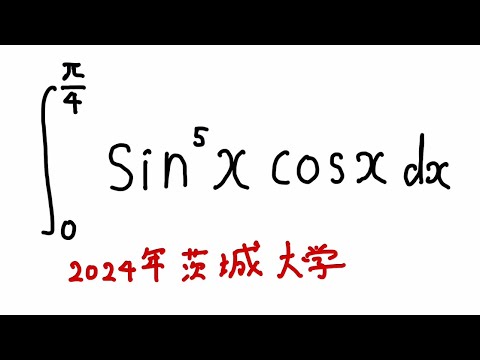
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}} \sin^5x\cos x$ $dx$
出典:2024年茨城大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} \sin^5x\cos x$ $dx$
出典:2024年茨城大学
#茨城大学#不定積分#ますただ
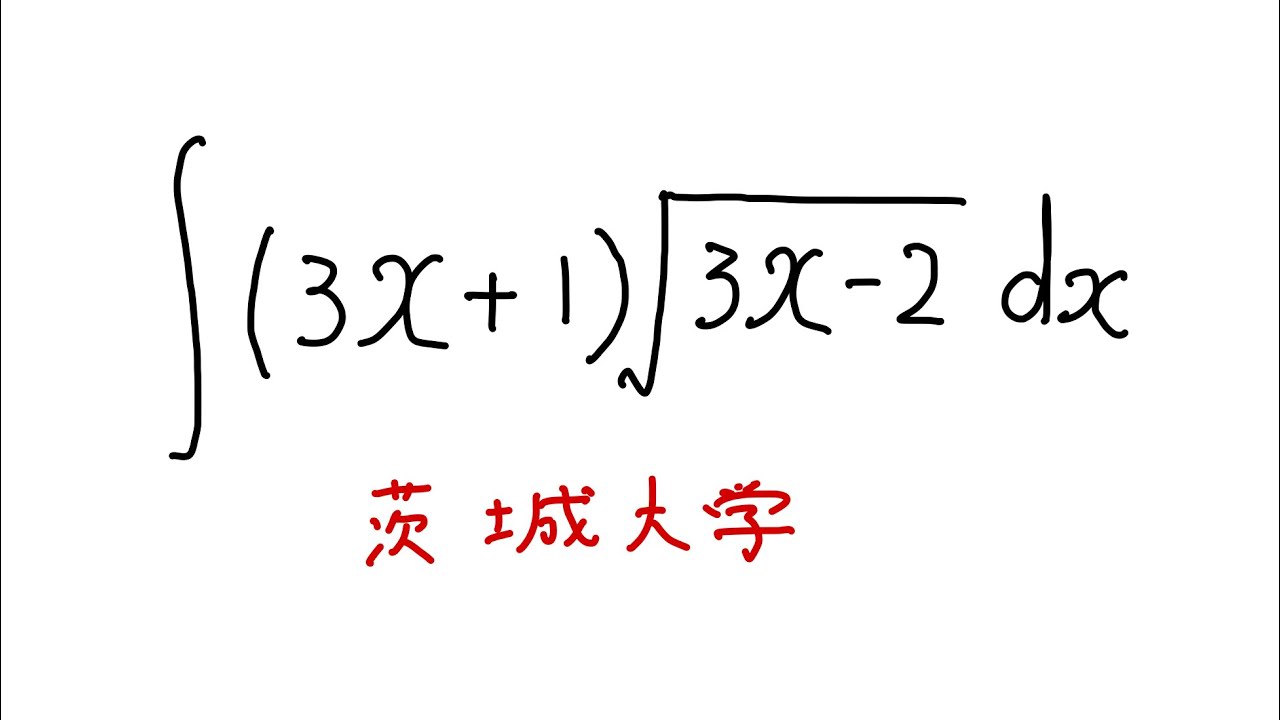
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int (3x+1)\sqrt{ 3x-2 }$ $dx$
出典:茨城大学
この動画を見る
$\displaystyle \int (3x+1)\sqrt{ 3x-2 }$ $dx$
出典:茨城大学
大学入試問題#825「まあまあ良問」 #茨城大学(2022) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-7}^{1}(2-x) \sqrt[ 3 ]{ 1-x }\ dx$
出典:2022年茨城大学
この動画を見る
$\displaystyle \int_{-7}^{1}(2-x) \sqrt[ 3 ]{ 1-x }\ dx$
出典:2022年茨城大学
#茨城大学(2023) #定積分 #Shorts
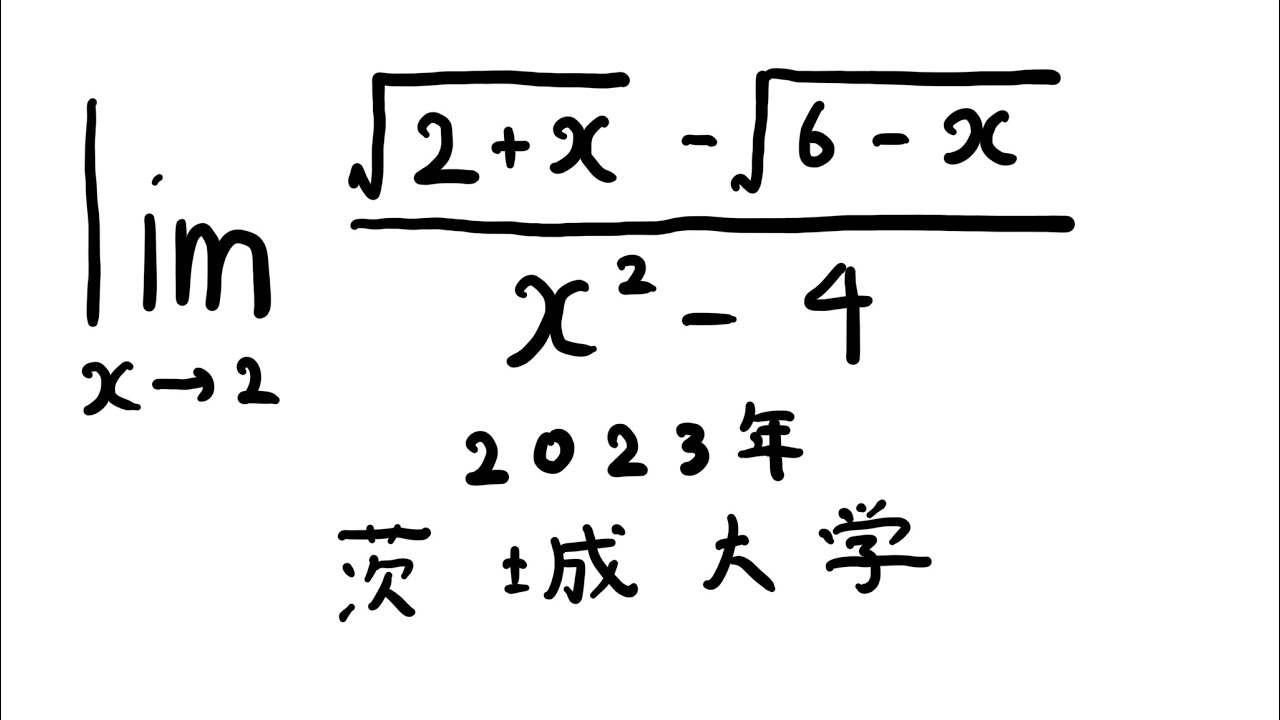
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 2 } \displaystyle \frac{\sqrt{ 2+x }-\sqrt{ 6-x }}{x^2-4}$
出典:2023年茨城大学
この動画を見る
$\displaystyle \lim_{ x \to 2 } \displaystyle \frac{\sqrt{ 2+x }-\sqrt{ 6-x }}{x^2-4}$
出典:2023年茨城大学
#茨城大学(2022) #定積分 #Shorts
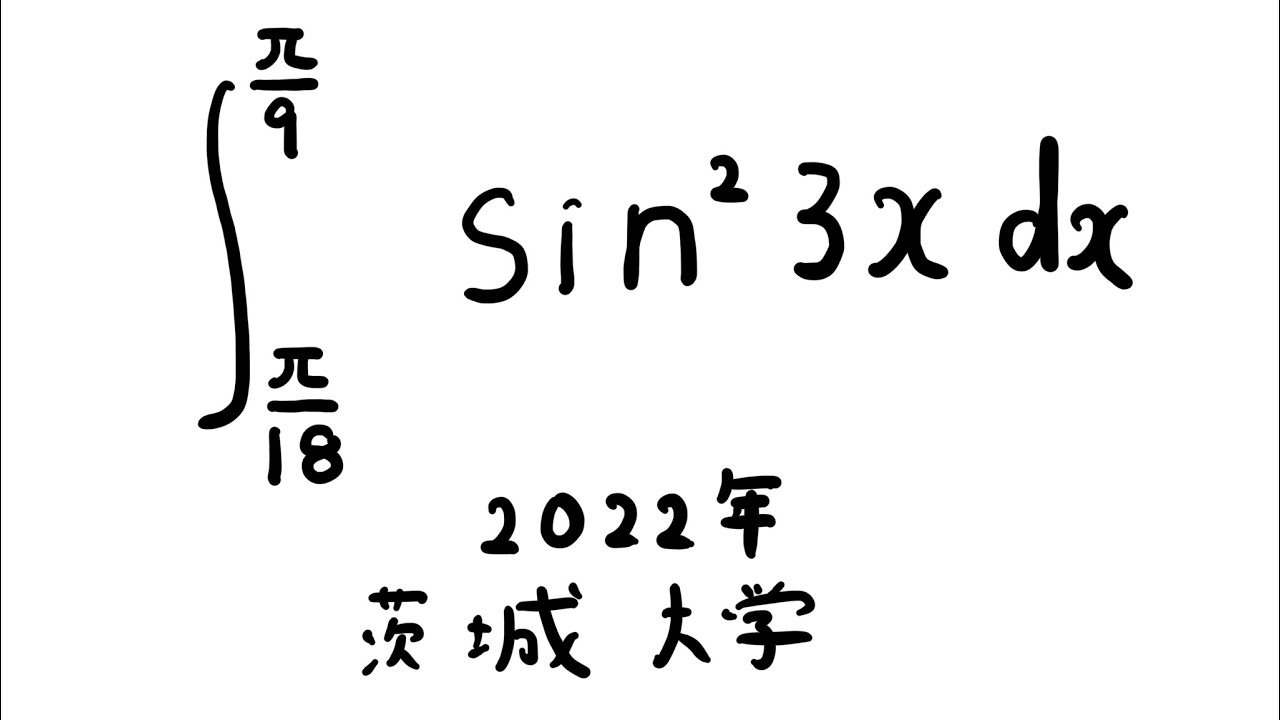
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{18}}^{\frac{\pi}{9}} \sin^23x\ dx$
出典:2022年茨城大学
この動画を見る
$\displaystyle \int_{\frac{\pi}{18}}^{\frac{\pi}{9}} \sin^23x\ dx$
出典:2022年茨城大学
#茨城大学(2022) #定積分 #Shorts
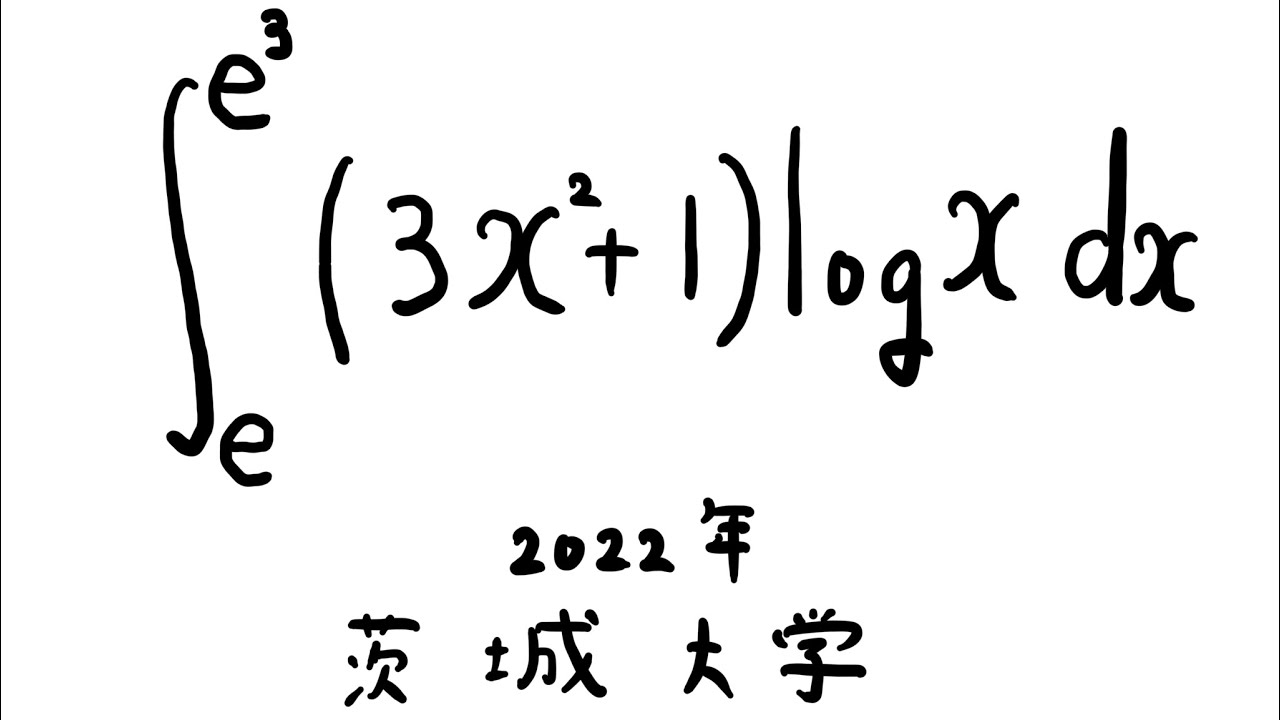
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{e}^{e^3} (3x^2+1)log\ x\ dx$
出典:2022年茨城大学
この動画を見る
$\displaystyle \int_{e}^{e^3} (3x^2+1)log\ x\ dx$
出典:2022年茨城大学
#茨城大学(2022) #定積分 #Shorts
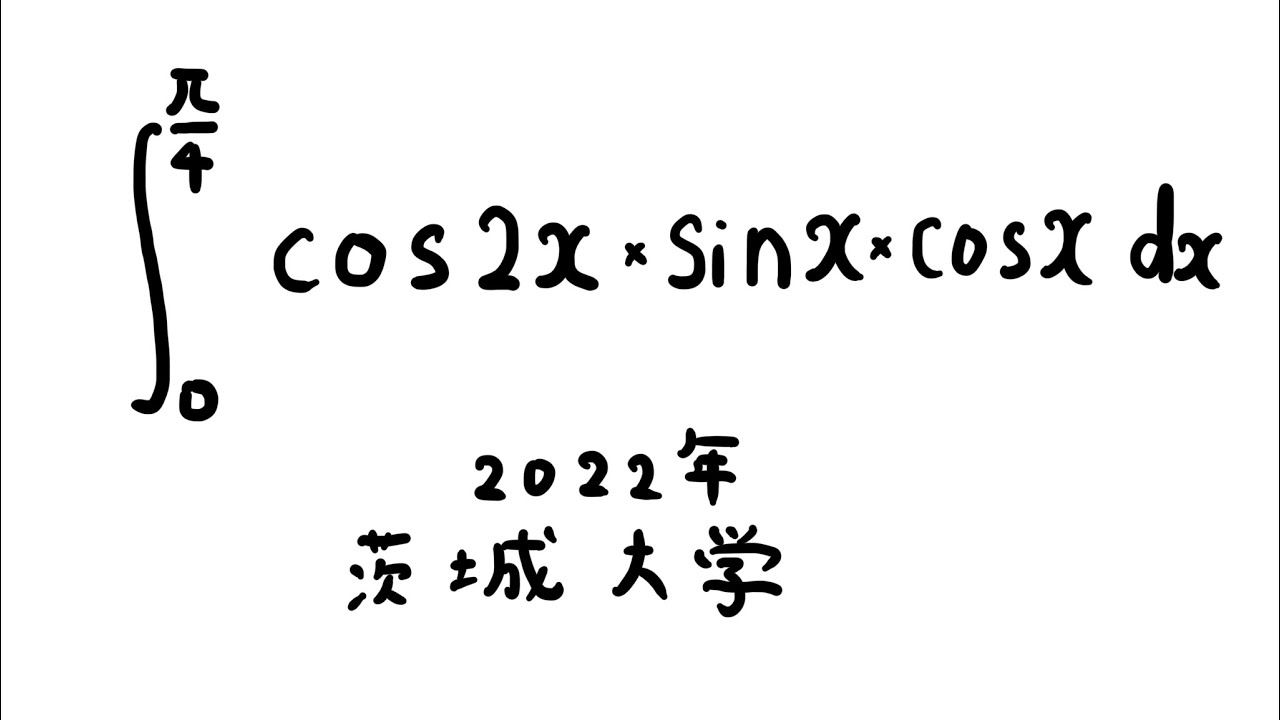
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}} \cos2x\times\sin\ x\ cos\ x\ dx$
出典:2022年茨城大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} \cos2x\times\sin\ x\ cos\ x\ dx$
出典:2022年茨城大学
#茨城大学(2023) #極限 #Shorts
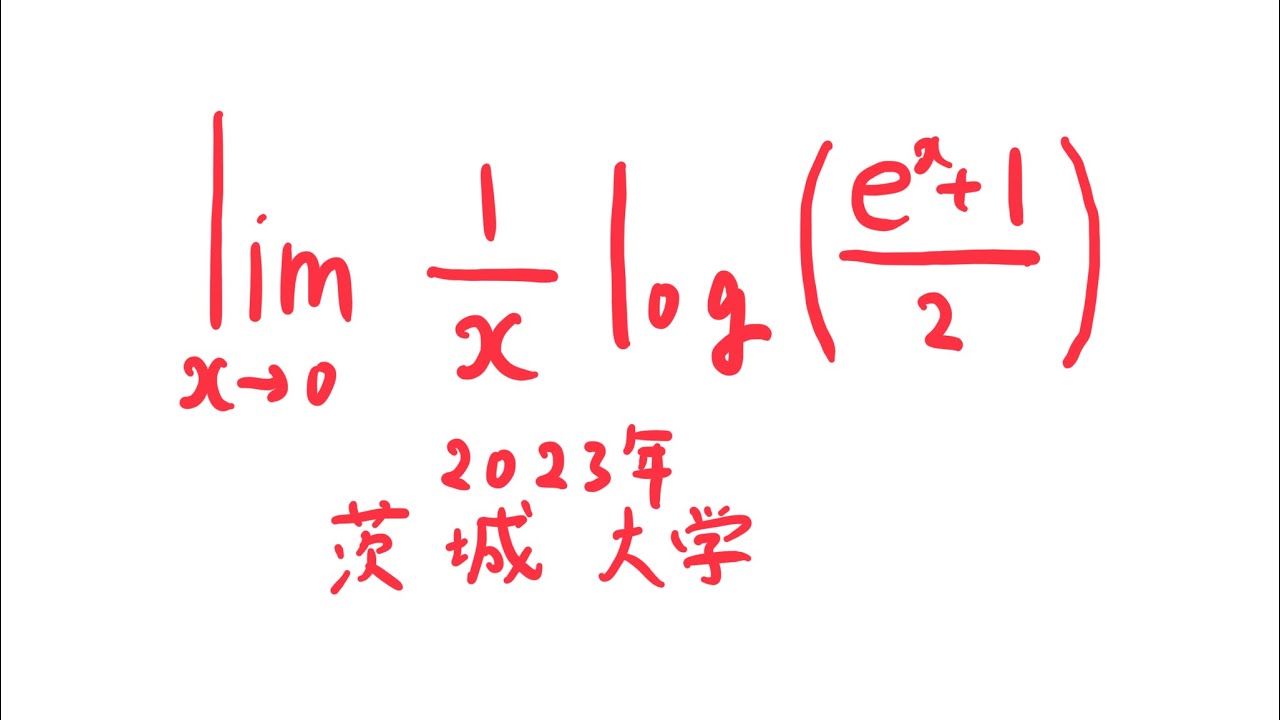
単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{1}{x}log(\displaystyle \frac{e^x+1}{2})$
出典:2023年茨城大学
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{1}{x}log(\displaystyle \frac{e^x+1}{2})$
出典:2023年茨城大学
#茨城大学(2023) #定積分 #Shorts
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
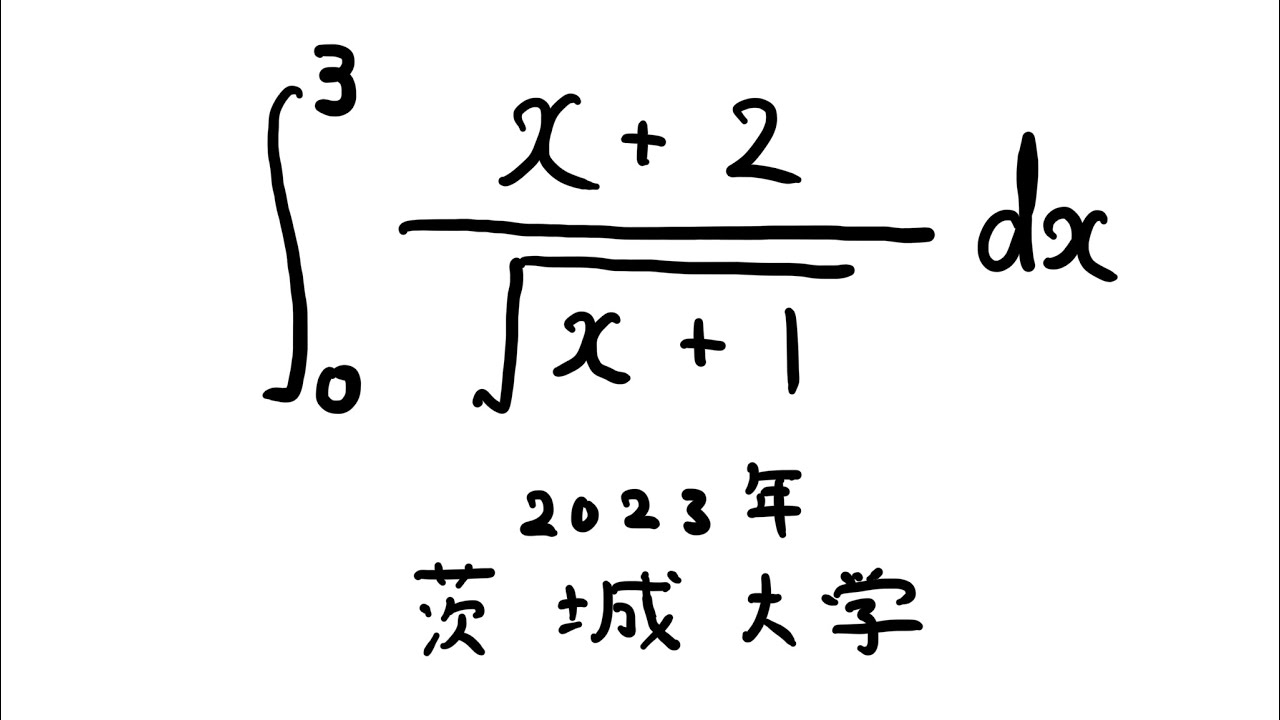
$\displaystyle \int_{0}^{3} \displaystyle \frac{x+2}{\sqrt{ x+1 }} dx$
出典:2023年茨城大学
この動画を見る
$\displaystyle \int_{0}^{3} \displaystyle \frac{x+2}{\sqrt{ x+1 }} dx$
出典:2023年茨城大学
#茨城大学(2023) #定積分 #Shorts
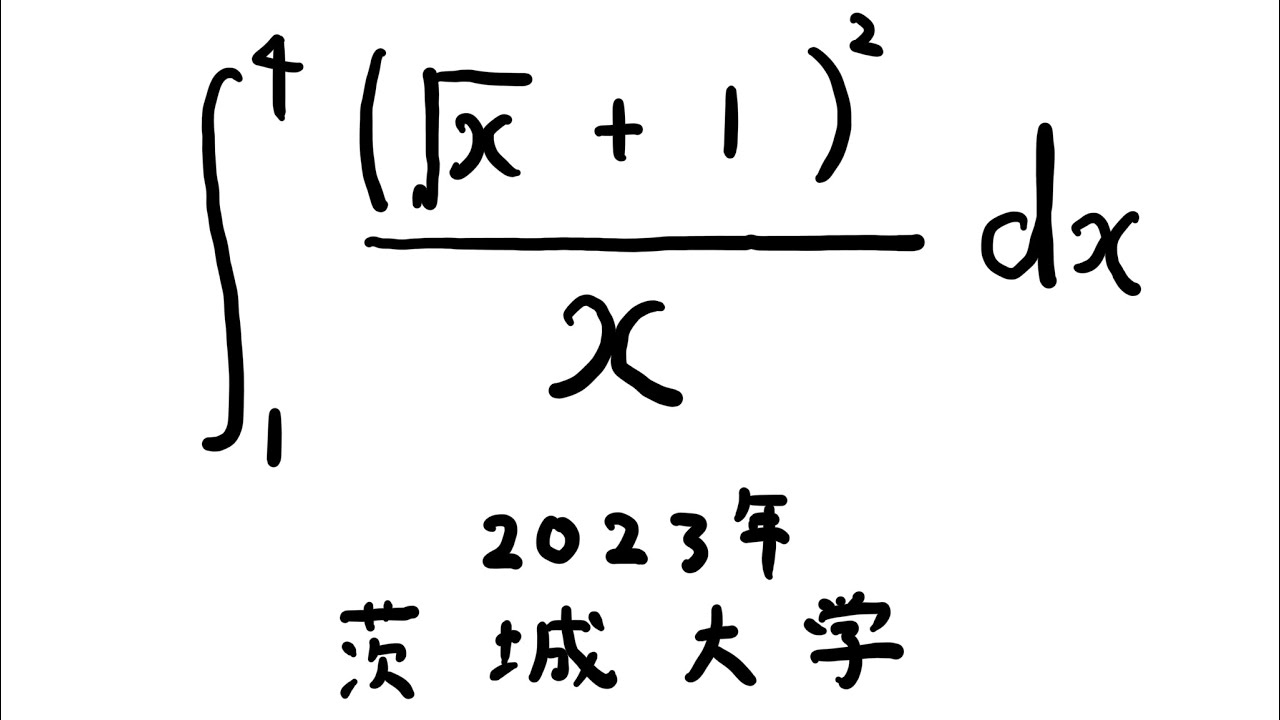
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{4} \displaystyle \frac{(\sqrt{ x }+1)^2}{x} dx$
出典:2023年茨城大学
この動画を見る
$\displaystyle \int_{1}^{4} \displaystyle \frac{(\sqrt{ x }+1)^2}{x} dx$
出典:2023年茨城大学
#茨城大学(2020) #定積分 #Shorts
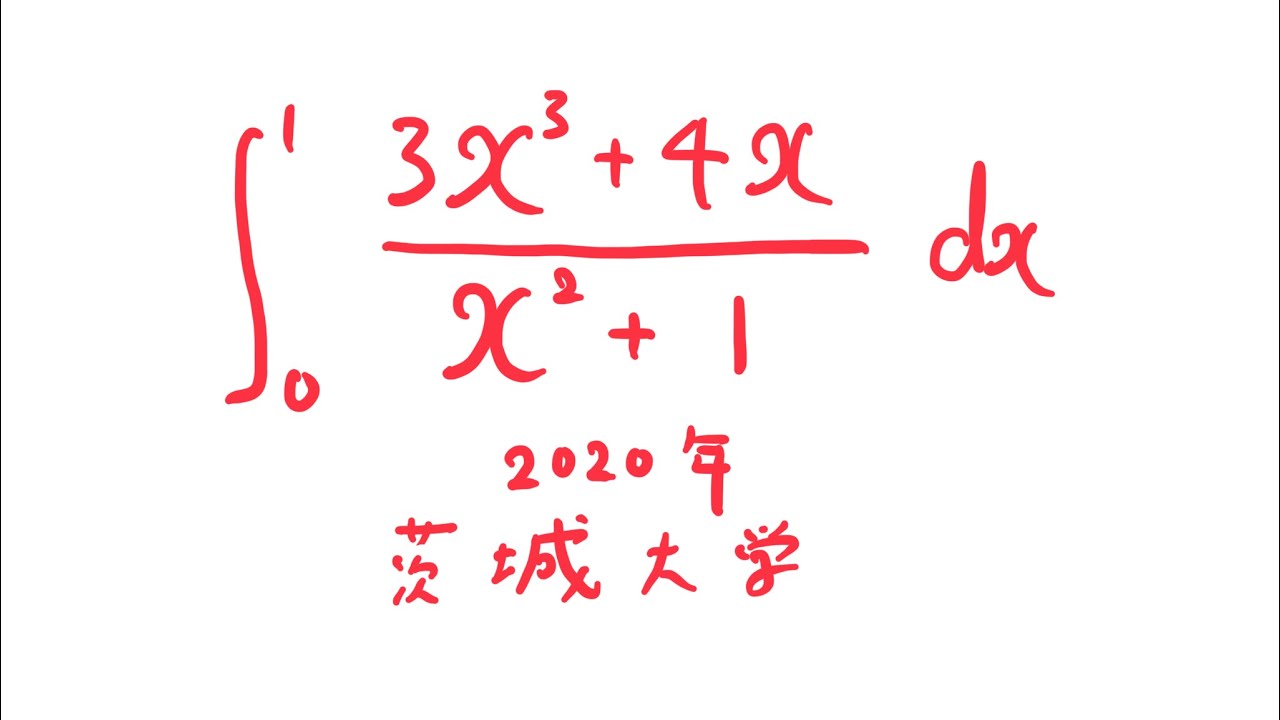
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{3x^3+4x}{x^2+1} dx$
出典:2020年茨城大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{3x^3+4x}{x^2+1} dx$
出典:2020年茨城大学
大学入試問題#591「技をかけたくなる積分」 茨城大学(2021) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1} (1+x+x^2)^2 dx$
出典:2021年茨城大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{1} (1+x+x^2)^2 dx$
出典:2021年茨城大学 入試問題
福田の1.5倍速演習〜合格する重要問題028〜九州大学2016年度文理共通問題〜余りと合同式

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#茨城大学
指導講師:
福田次郎
問題文全文(内容文):
自然数nに対して、$10^n$を13で割った余りを$a_n$とおく。$a_n$は0から12まで
の整数である。以下の問いに答えよ。
(1)$a_{n+1}$は$10a_n$を13で割った余りに等しいことを示せ。
(2)$a_1,a_2,a_3,\cdots,a_6$を求めよ。
(3)以下の3条件を満たす自然数Nをすべて求めよ。
$(\textrm{i})N$を十進法で表示した時6桁となる。
$(\textrm{ii})N$を十進法で表示して、最初と最後の桁の数字を取り除くと
2016となる。
$(\textrm{iii})N$は13で割り切れる。
2016九州大学文理過去問
この動画を見る
自然数nに対して、$10^n$を13で割った余りを$a_n$とおく。$a_n$は0から12まで
の整数である。以下の問いに答えよ。
(1)$a_{n+1}$は$10a_n$を13で割った余りに等しいことを示せ。
(2)$a_1,a_2,a_3,\cdots,a_6$を求めよ。
(3)以下の3条件を満たす自然数Nをすべて求めよ。
$(\textrm{i})N$を十進法で表示した時6桁となる。
$(\textrm{ii})N$を十進法で表示して、最初と最後の桁の数字を取り除くと
2016となる。
$(\textrm{iii})N$は13で割り切れる。
2016九州大学文理過去問
大学入試問題#252 茨城大学(2012) #定積分

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#指数関数と対数関数#対数関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{log2}e^{|x|}e^xdx$を計算せよ。
出典:2012年茨城大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{log2}e^{|x|}e^xdx$を計算せよ。
出典:2012年茨城大学 入試問題
大学入試問題#236 茨城大学(2012) 改 #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{1}{x^2}(1+\displaystyle \frac{2}{x})^4dx$を計算せよ。
出典:2012年茨城大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{1}{x^2}(1+\displaystyle \frac{2}{x})^4dx$を計算せよ。
出典:2012年茨城大学 入試問題
数学「大学入試良問集」【17−8 不等式とハサミウチの原理】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の各問いに答えよ。
(1)
$h \gt 0$として、不等式$(1+h)^n \geqq 1+nh+\displaystyle \frac{n(n-1)}{2}h^2$がすべての自然数$n$について成り立つことを数学的帰納法を用いて説明せよ。
(2)
(1)の不等式を使って、$0 \lt x \lt 1$のとき、数列$\{nx^n\}$が$0$に収束することを示せ。
(3)
$0 \lt x \lt 1$のとき
無限級数$2x+4x^2+6x^3+・・・+2nx^n+・・・$の和を求めよ。
この動画を見る
次の各問いに答えよ。
(1)
$h \gt 0$として、不等式$(1+h)^n \geqq 1+nh+\displaystyle \frac{n(n-1)}{2}h^2$がすべての自然数$n$について成り立つことを数学的帰納法を用いて説明せよ。
(2)
(1)の不等式を使って、$0 \lt x \lt 1$のとき、数列$\{nx^n\}$が$0$に収束することを示せ。
(3)
$0 \lt x \lt 1$のとき
無限級数$2x+4x^2+6x^3+・・・+2nx^n+・・・$の和を求めよ。
茨城大 不等式の証明 (補)3数の相加相乗平均証明

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)#茨城大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2+y^2+z^2 \geqq ax(y-z)$がすべての実数$x,y,z$について成り立つ実数$a$の範囲を求めよ
出典:2000年茨城大学 過去問
この動画を見る
$x^2+y^2+z^2 \geqq ax(y-z)$がすべての実数$x,y,z$について成り立つ実数$a$の範囲を求めよ
出典:2000年茨城大学 過去問
茨城大 3次関数と接線 積分 1/12公式導出

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#接線と法線・平均値の定理#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#茨城大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^3-4x$と$(a,f(a))$における接線とで囲まれた面積$(a \neq 0)$
出典:1994年茨城大学 過去問
この動画を見る
$f(x)=x^3-4x$と$(a,f(a))$における接線とで囲まれた面積$(a \neq 0)$
出典:1994年茨城大学 過去問
茨城大 二次関数

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#茨城大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^2-(a-2)x+2$
$g(x)=-x^2+2x+a-2$
(1)
すべての実数$x$に対して$f(x) \gt g(x)$が成り立つ
(2)
すべての実数$x_1,x_2$に対して$f(x_1) \gt g(x_2)$が成り立つ
(1)(2)ともに$a$の値の範囲
この動画を見る
$f(x)=x^2-(a-2)x+2$
$g(x)=-x^2+2x+a-2$
(1)
すべての実数$x$に対して$f(x) \gt g(x)$が成り立つ
(2)
すべての実数$x_1,x_2$に対して$f(x_1) \gt g(x_2)$が成り立つ
(1)(2)ともに$a$の値の範囲
茨城大 確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#整数の性質#確率#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#茨城大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
サイコロを4回振って出た目を順に$a,b,c,d$
(1)
$a^2+b^2+c^2+d^2$が4の倍数になる確率を求めよ
(2)
積$abcd$が4の倍数となる確率を求めよ
出典:2010年茨城大学 過去問
この動画を見る
サイコロを4回振って出た目を順に$a,b,c,d$
(1)
$a^2+b^2+c^2+d^2$が4の倍数になる確率を求めよ
(2)
積$abcd$が4の倍数となる確率を求めよ
出典:2010年茨城大学 過去問
茨城大 整数問題 Mathematics Japanese university entrance exam

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#茨城大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)
$21^{2015}$を$400$で割った余りを求めよ
(2)
$2^{2x+1}+1$は$3$の倍数
出典:茨城大学 過去問
この動画を見る
(1)
$21^{2015}$を$400$で割った余りを求めよ
(2)
$2^{2x+1}+1$は$3$の倍数
出典:茨城大学 過去問
茨城大 複素数 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#茨城大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha=\displaystyle \frac{\sqrt{ 2 }}{2}+\displaystyle \frac{\sqrt{ 2 }}{2}i,\beta=-\displaystyle \frac{\sqrt{ 3 }}{2}+\displaystyle \frac{1}{2}i$
(1)
$\alpha^{n}=\beta^n=1$を満たす最小の自然数$n$
(2)
$n$自然数、$1 \leqq n \leqq 20$
$|\alpha^n+\beta^n|$の最小値とそのときの$n$の値は?
出典:2005年茨城大学 過去問
この動画を見る
$\alpha=\displaystyle \frac{\sqrt{ 2 }}{2}+\displaystyle \frac{\sqrt{ 2 }}{2}i,\beta=-\displaystyle \frac{\sqrt{ 3 }}{2}+\displaystyle \frac{1}{2}i$
(1)
$\alpha^{n}=\beta^n=1$を満たす最小の自然数$n$
(2)
$n$自然数、$1 \leqq n \leqq 20$
$|\alpha^n+\beta^n|$の最小値とそのときの$n$の値は?
出典:2005年茨城大学 過去問
近畿大 茨城大 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#複素数平面#学校別大学入試過去問解説(数学)#近畿大学#数学(高校生)#数C#茨城大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
近畿大学過去問題
$x^4-Px^2+P^2-P-2=0$が相異4実根をもつPの範囲
茨城大学過去問題
$x^3=i$を解け
この動画を見る
近畿大学過去問題
$x^4-Px^2+P^2-P-2=0$が相異4実根をもつPの範囲
茨城大学過去問題
$x^3=i$を解け
