 関西学院大学
関西学院大学
 関西学院大学
関西学院大学
#関西学院大学2011#方程式_69

単元:
#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$(x+1)(x-2)(x+3)(x-4)=-24$を解け.
2011関西学院大学過去問題
この動画を見る
$(x+1)(x-2)(x+3)(x-4)=-24$を解け.
2011関西学院大学過去問題
#関西学院大学2006#不定積分_68
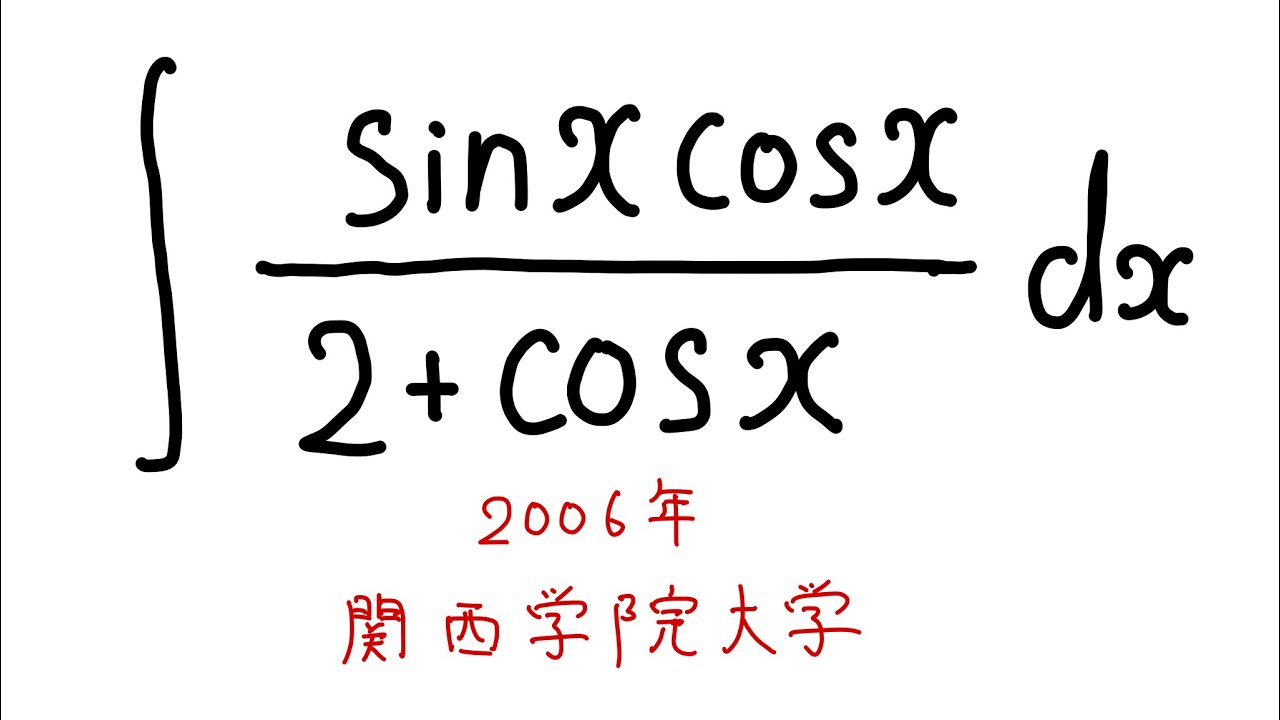
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#関西学院大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \dfrac{\sin x \cos x}{2+\cos \ x} dx$を解け.
2006関西学院大学過去問
この動画を見る
$\displaystyle \int \dfrac{\sin x \cos x}{2+\cos \ x} dx$を解け.
2006関西学院大学過去問
#関西学院大学2019#不定積分_67
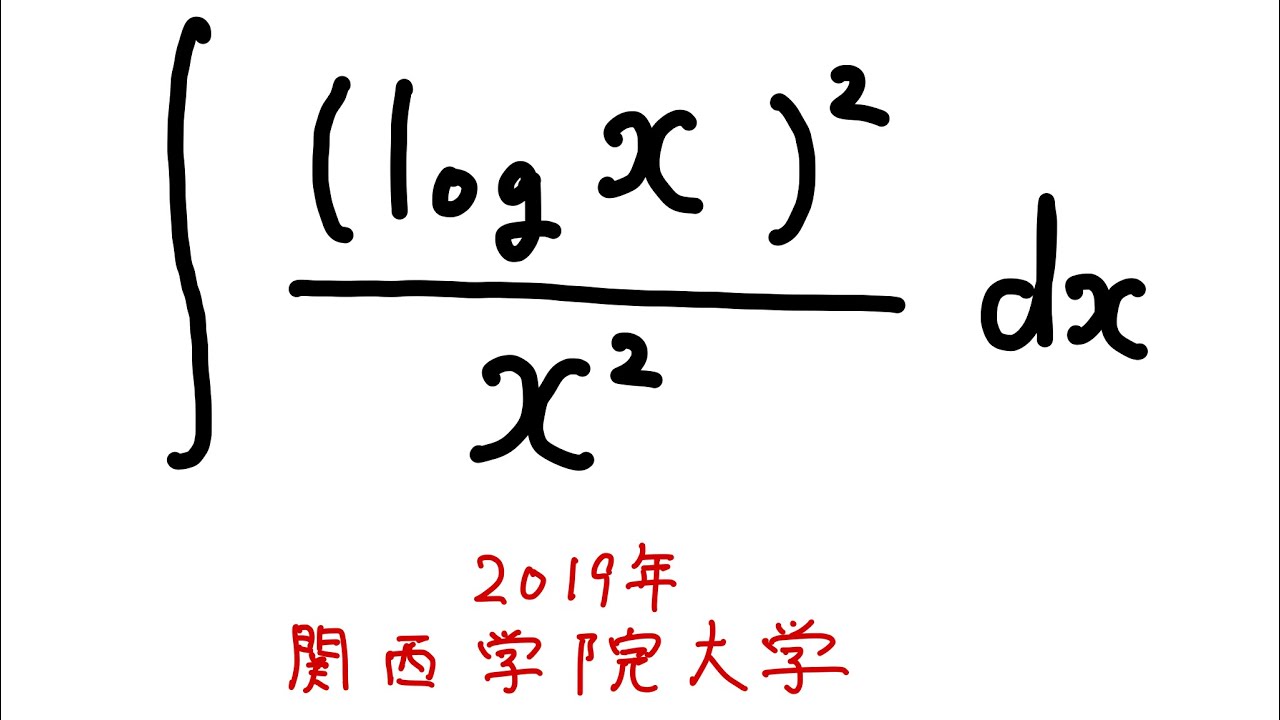
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#関西学院大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \dfrac{(\log x)^2}{x^2} dx$を解け.
2019関西学院大学過去問
この動画を見る
$\displaystyle \int \dfrac{(\log x)^2}{x^2} dx$を解け.
2019関西学院大学過去問
#関西学院大学2006#不定積分_66
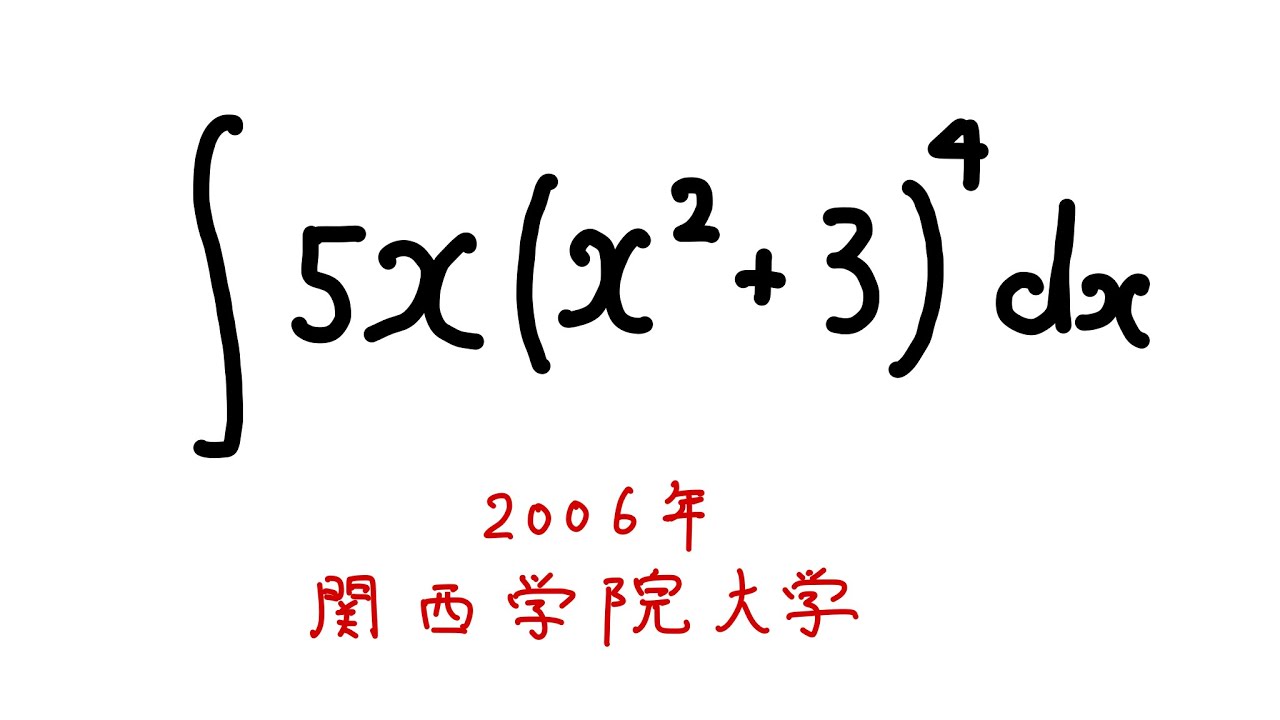
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#関西学院大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$ \int 5x(x^2+3)^4 \ dx$を解け.
2006関西学院大学過去問
この動画を見る
$ \int 5x(x^2+3)^4 \ dx$を解け.
2006関西学院大学過去問
#関西学院大学2012 #不定積分
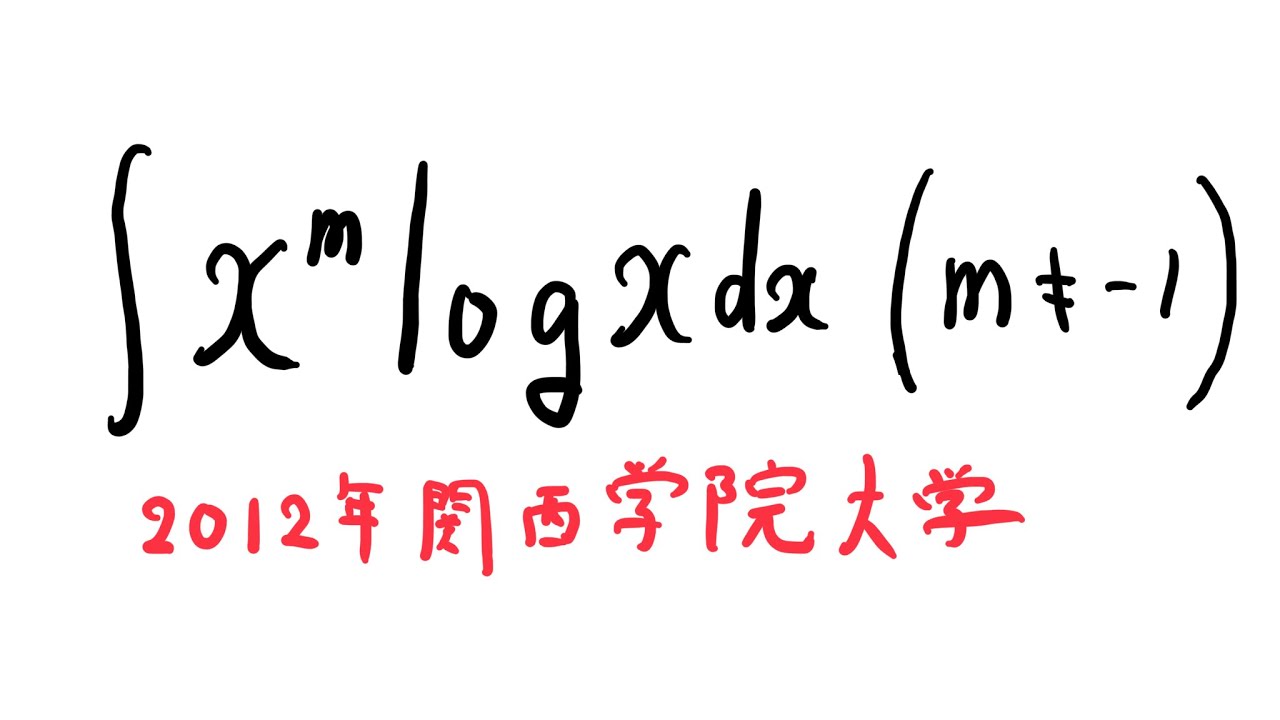
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int x^m log$ $x$ $dx(m \neq -1)$
出典:2012年関西学院大学
この動画を見る
$\displaystyle \int x^m log$ $x$ $dx(m \neq -1)$
出典:2012年関西学院大学
関西学院大 3次方程式の解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2022関西学院大学過去問題
a実数
$x^3-(2a+1)x^2-3(a-1)x-a+5 = 0$
①aの値に関わらずx=□は解である
②異なる3つの負の解をもつaの範囲
③$x^3=1$の虚数解の1つをωとする
ω+k(k>0)が解であるならa=□
この動画を見る
2022関西学院大学過去問題
a実数
$x^3-(2a+1)x^2-3(a-1)x-a+5 = 0$
①aの値に関わらずx=□は解である
②異なる3つの負の解をもつaの範囲
③$x^3=1$の虚数解の1つをωとする
ω+k(k>0)が解であるならa=□
高等学校入学試験予想問題:関西学院高等部~全部入試問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
・$(\sqrt{ 5 }-2)(\sqrt{ 5 }+3)-\displaystyle \frac{(\sqrt{ 7 }-2)(\sqrt{ 7 }+\sqrt{ 7 })}{\sqrt{ 20 }}
を計算せよ。
【連立方程式】
$(x+3y):(4x-2y)=3:5$
$3x-5y=12$
$x$と$y$を求めよ。
1から9の数字が書かれたカードが 1枚ずつある。この9枚のカードから3枚を
選んで左から並べて3桁の整数を作る。
(1)整数は全部でいくつか。
(2)偶数はいくつか。
(3) 4の倍数はいくつか。
(4)3の倍数はいくつか
を求めよ。
この動画を見る
・$(\sqrt{ 5 }-2)(\sqrt{ 5 }+3)-\displaystyle \frac{(\sqrt{ 7 }-2)(\sqrt{ 7 }+\sqrt{ 7 })}{\sqrt{ 20 }}
を計算せよ。
【連立方程式】
$(x+3y):(4x-2y)=3:5$
$3x-5y=12$
$x$と$y$を求めよ。
1から9の数字が書かれたカードが 1枚ずつある。この9枚のカードから3枚を
選んで左から並べて3桁の整数を作る。
(1)整数は全部でいくつか。
(2)偶数はいくつか。
(3) 4の倍数はいくつか。
(4)3の倍数はいくつか
を求めよ。
大学入試問題#129 関西学院大学(1991) 二項定理の応用

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$(a+b+\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b})^7$を展開した時の$ab^2$の係数を求めよ。
出典:1991年関西学院大学 入試問題
この動画を見る
$(a+b+\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b})^7$を展開した時の$ab^2$の係数を求めよ。
出典:1991年関西学院大学 入試問題
大学入試問題#91 関西学院大学(2006) 不定積分
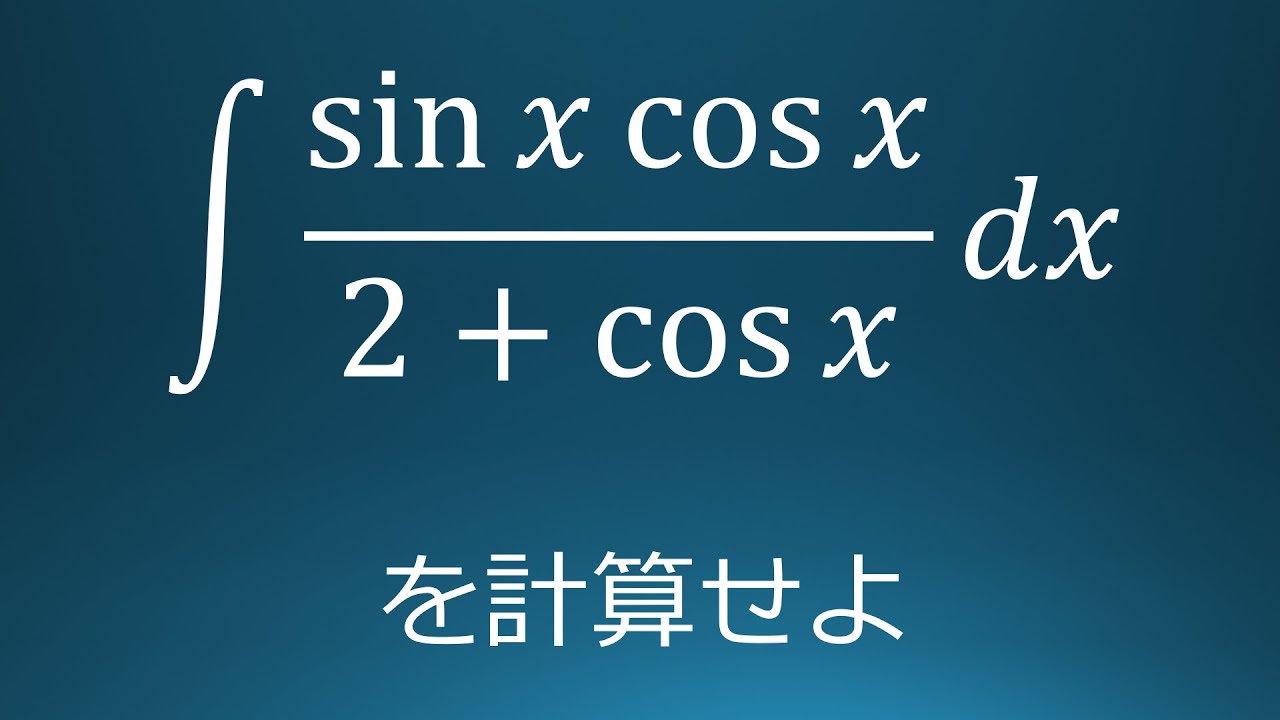
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{\sin\ x\ \cos\ x}{2+\cos\ x}\ dx$を計算せよ。
出典:2006年関西学院大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{\sin\ x\ \cos\ x}{2+\cos\ x}\ dx$を計算せよ。
出典:2006年関西学院大学 入試問題
【数A】整数の性質:関西学院大学 背理法の利用

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
pを整数とする。
方程式$x^2+4x-5p+2=0$を満足する整数xは存在しないことを証明せよ。
この動画を見る
pを整数とする。
方程式$x^2+4x-5p+2=0$を満足する整数xは存在しないことを証明せよ。
数学「大学入試良問集」【5−8 余事象の確率①】を宇宙一わかりやすく

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
偶数の目が出る確率が$\displaystyle \frac{2}{3}$であるような、目の出方にかたよりのあるサイコロが2個あり、これらを同時に投げるゲームを行う。
、これらを同時に投げるゲームを行う。
両方とも偶数の目が出たら当たり、両方とも奇数の目が出たら大当たりとする。
このゲームを$n$回繰り返すとき、次の問いに答えよ。
(1)大当たりが少なくとも1回は出る確率を求めよ。
(2)当たりまたは大当たりが少なくとも1回は出る確率を求めよ。
(3)当たりと大当たりのいずれもが少なくとも1回は出る確率を求めよ
この動画を見る
偶数の目が出る確率が$\displaystyle \frac{2}{3}$であるような、目の出方にかたよりのあるサイコロが2個あり、これらを同時に投げるゲームを行う。
、これらを同時に投げるゲームを行う。
両方とも偶数の目が出たら当たり、両方とも奇数の目が出たら大当たりとする。
このゲームを$n$回繰り返すとき、次の問いに答えよ。
(1)大当たりが少なくとも1回は出る確率を求めよ。
(2)当たりまたは大当たりが少なくとも1回は出る確率を求めよ。
(3)当たりと大当たりのいずれもが少なくとも1回は出る確率を求めよ
関西学院大 漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$P$自然数、$a_1=2-\displaystyle \frac{1}{2^p}$
$a_{n+1}=2a_n-n$
一般項を求めよ
{$a_n$}の最大値とそれを与える$n$を求めよ
出典:2005年関西学院大学 過去問
この動画を見る
$P$自然数、$a_1=2-\displaystyle \frac{1}{2^p}$
$a_{n+1}=2a_n-n$
一般項を求めよ
{$a_n$}の最大値とそれを与える$n$を求めよ
出典:2005年関西学院大学 過去問
