関西医科大学
関西医科大学
大学入試問題#735「因数分解だからと舐めプ厳禁」 関西医科大学(2016)因数分解
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師：
ますただ
問題文全文(内容文)：
$x(x+9)(x-4)(x-13)+2016$を因数分解せよ
出典：2016年関西医科大学 入試問題
この動画を見る
$x(x+9)(x-4)(x-13)+2016$を因数分解せよ
出典：2016年関西医科大学 入試問題
大学入試問題#729「医学部なら落とせん」 関西医科大学(2021) 整数問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師：
ますただ
問題文全文(内容文)：
$x^2-|x|y+y^2=3$を満たす整数の組$(x,y)$をすべて求めよ。
出典：2021年関西医科大学 入試問題
この動画を見る
$x^2-|x|y+y^2=3$を満たす整数の組$(x,y)$をすべて求めよ。
出典：2021年関西医科大学 入試問題
関西医科大学 2011 極限
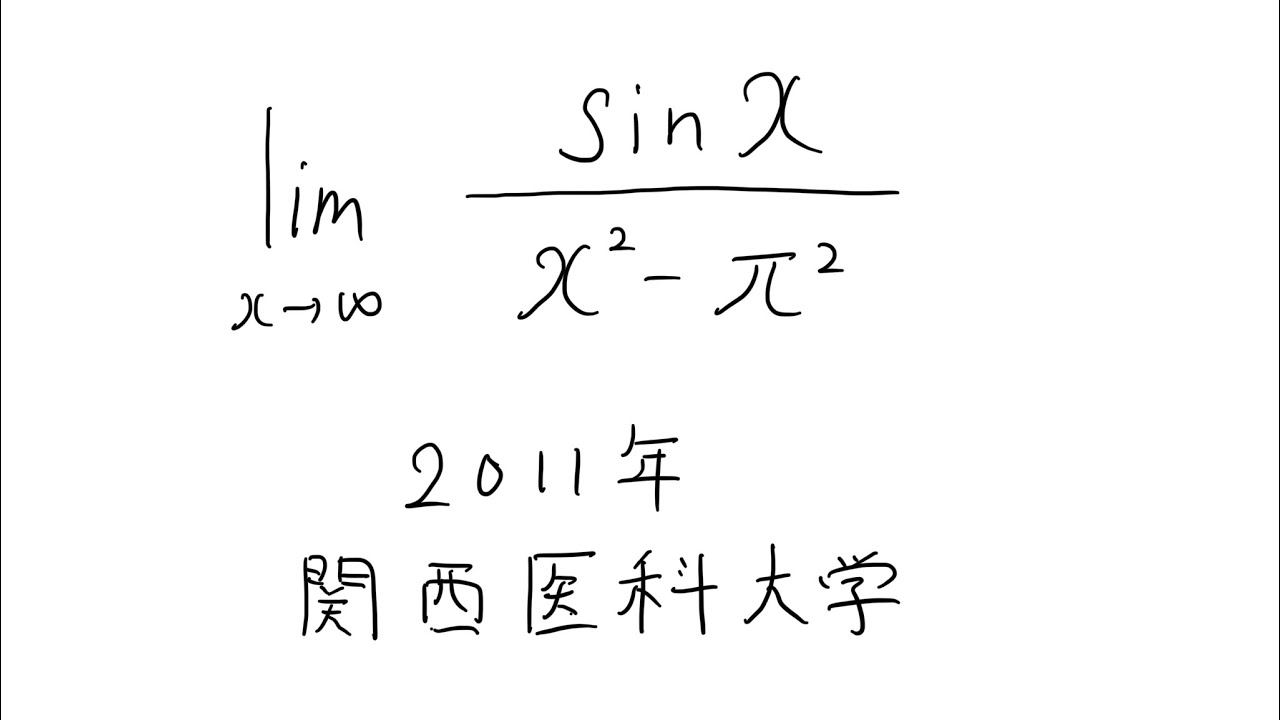
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to \pi } \displaystyle \frac{\sin\ x}{x^2-\pi^2}$
出典：2011年関西医科大学
この動画を見る
$\displaystyle \lim_{ x \to \pi } \displaystyle \frac{\sin\ x}{x^2-\pi^2}$
出典：2011年関西医科大学
大学入試問題#710「入試開始の初手この問題！！」 関西医科大学(2023)整数問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師：
ますただ
問題文全文(内容文)：
$(a+1)(a-1)(b+1)(b-1)=4ab$ を満たす整数の組$(a,b)$をすべて求めよ。
ただし、$a \lt b$とする。
出典：2023年関西医科大学 入試問題
この動画を見る
$(a+1)(a-1)(b+1)(b-1)=4ab$ を満たす整数の組$(a,b)$をすべて求めよ。
ただし、$a \lt b$とする。
出典：2023年関西医科大学 入試問題
関西医科大学 #極限 #Shorts
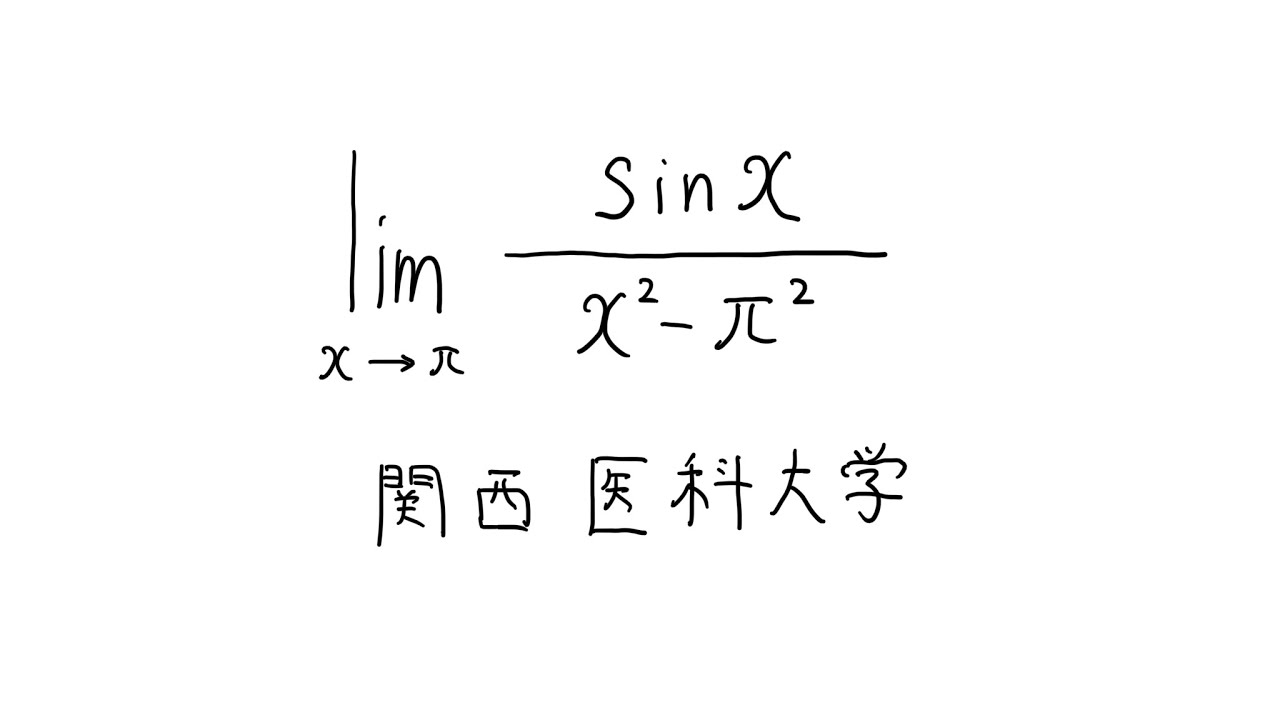
単元：
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#関西医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to \pi } \displaystyle \frac{\sin\ x}{x^2-\pi^2}$を求めよ
出典：関西医科大学
この動画を見る
$\displaystyle \lim_{ x \to \pi } \displaystyle \frac{\sin\ x}{x^2-\pi^2}$を求めよ
出典：関西医科大学
漸化式 関西医科大
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#関西医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2021関西医科大学過去問題
$a_1=\frac{1}{13}$ n=1,2,・・・自然数
$5a_{n+1}=10a_n-a_{n+1}・a_n$
一般項$a_n$を求めよ
この動画を見る
2021関西医科大学過去問題
$a_1=\frac{1}{13}$ n=1,2,・・・自然数
$5a_{n+1}=10a_n-a_{n+1}・a_n$
一般項$a_n$を求めよ
関西医科大 分数不等式 整数問題
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#関西医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2022関西医科大学過去問題
$f(x)=\frac{6x^2+17x+10}{3x-2}$
①$f(x)>0$をみたすxの範囲
②f(n)が正の整数となる整数n
この動画を見る
2022関西医科大学過去問題
$f(x)=\frac{6x^2+17x+10}{3x-2}$
①$f(x)>0$をみたすxの範囲
②f(n)が正の整数となる整数n
関西医科大 対数方程式の基礎
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2020関西医科大学過去問題
$\log_4(2x^2)-\log_x4+\frac{1}{2}=0$
この動画を見る
2020関西医科大学過去問題
$\log_4(2x^2)-\log_x4+\frac{1}{2}=0$
三角関数の極限
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#関西医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
関西医科大学過去問題
$\displaystyle\lim_{(x \to \pi)}\frac{sinx}{x^2-\pi^2}$
この動画を見る
関西医科大学過去問題
$\displaystyle\lim_{(x \to \pi)}\frac{sinx}{x^2-\pi^2}$
関西医科大
単元：
#数Ⅰ#数A#大学入試過去問(数学)#数と式#式の計算（整式・展開・因数分解）#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$3x^2+xy-2y^2-x+4y=4$をみたす整数(x,y)を求めよ.
関西医科大過去問
この動画を見る
$3x^2+xy-2y^2-x+4y=4$をみたす整数(x,y)を求めよ.
関西医科大過去問
2022関西医科 超基本問題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x=\displaystyle \frac{6x^2+17x+10}{3x-2}$
(1)$f(x) \gt 0$を解け
(2)$f(n)$の値が自然数となる整数$n$
を求めよ。
2022年 関西医科過去問
この動画を見る
$x=\displaystyle \frac{6x^2+17x+10}{3x-2}$
(1)$f(x) \gt 0$を解け
(2)$f(n)$の値が自然数となる整数$n$
を求めよ。
2022年 関西医科過去問