高知工科大学
高知工科大学
#高知工科大学2024#定積分_27#元高校教員
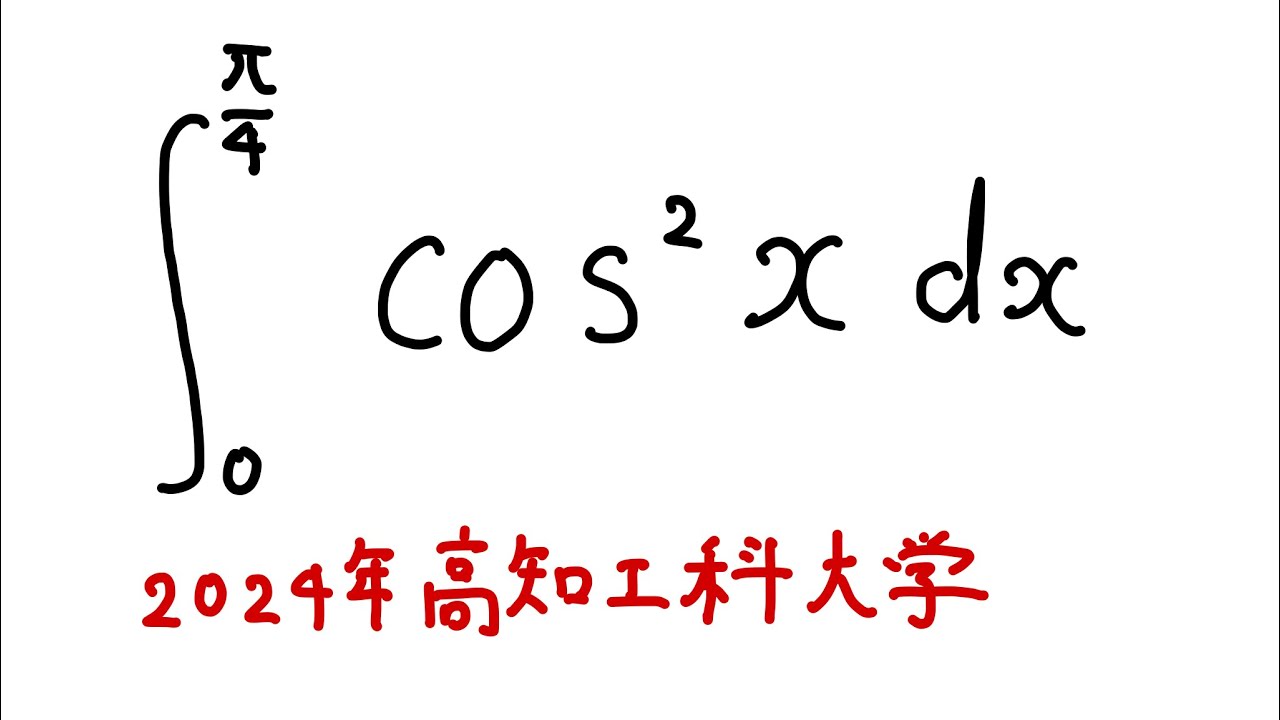
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#高知工科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{4}} \cos^2x dx$
出典：2024年高知工科大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} \cos^2x dx$
出典：2024年高知工科大学
#高知工科大学2024#定積分_25#元高校教員
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#高知工科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-1}^{3} x|x-2| dx$
出典：2024年 高知工科大学
この動画を見る
$\displaystyle \int_{-1}^{3} x|x-2| dx$
出典：2024年 高知工科大学
#高知工科大学2020 #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#高知工科大学
指導講師：
ますただ
問題文全文(内容文)：
以下の定積分を解け。
$\displaystyle \int_{1}^{\sqrt{ e }} \displaystyle \frac{(log x)^3}{x} dx$
出典：2020年高知工科大学
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{1}^{\sqrt{ e }} \displaystyle \frac{(log x)^3}{x} dx$
出典：2020年高知工科大学
#高知工科大学(2021)
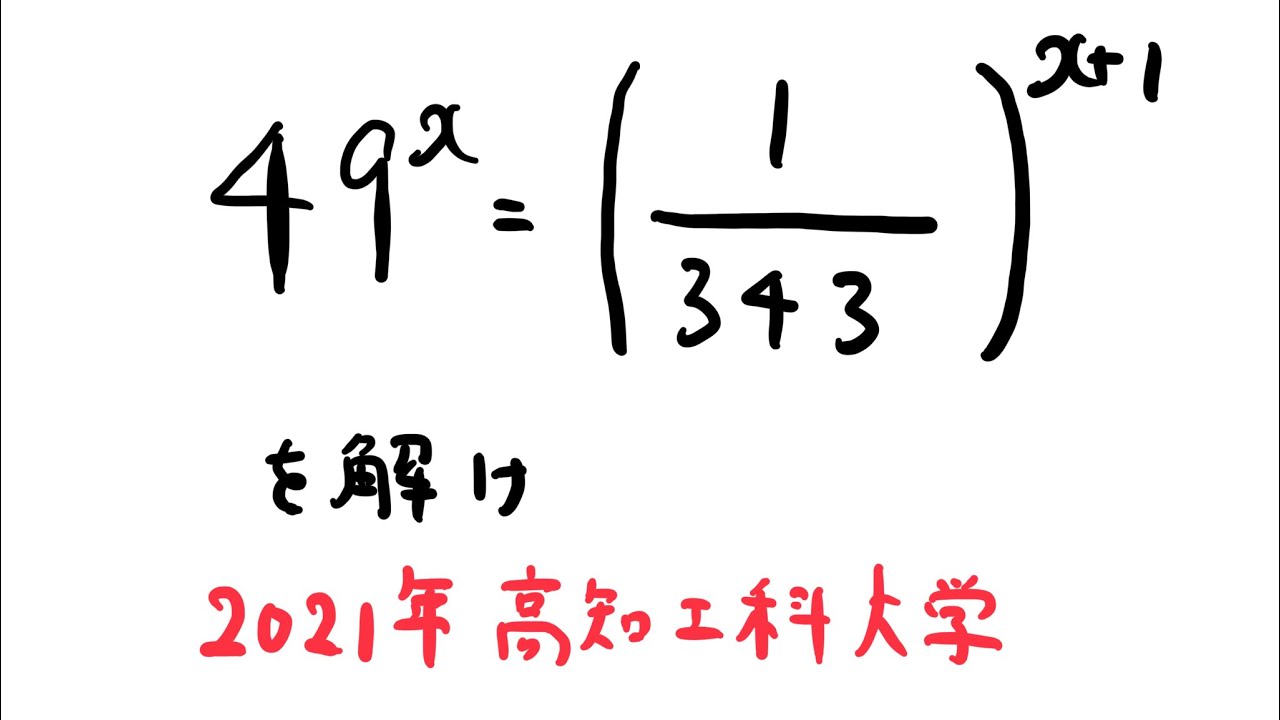
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#数学(高校生)#高知工科大学
指導講師：
ますただ
問題文全文(内容文)：
$49^=(\displaystyle \frac{1}{343})^{x+1}$を解け
出典：2021年高知工科大学
この動画を見る
$49^=(\displaystyle \frac{1}{343})^{x+1}$を解け
出典：2021年高知工科大学
#高知工科大学(2023) #定積分 #Shorts
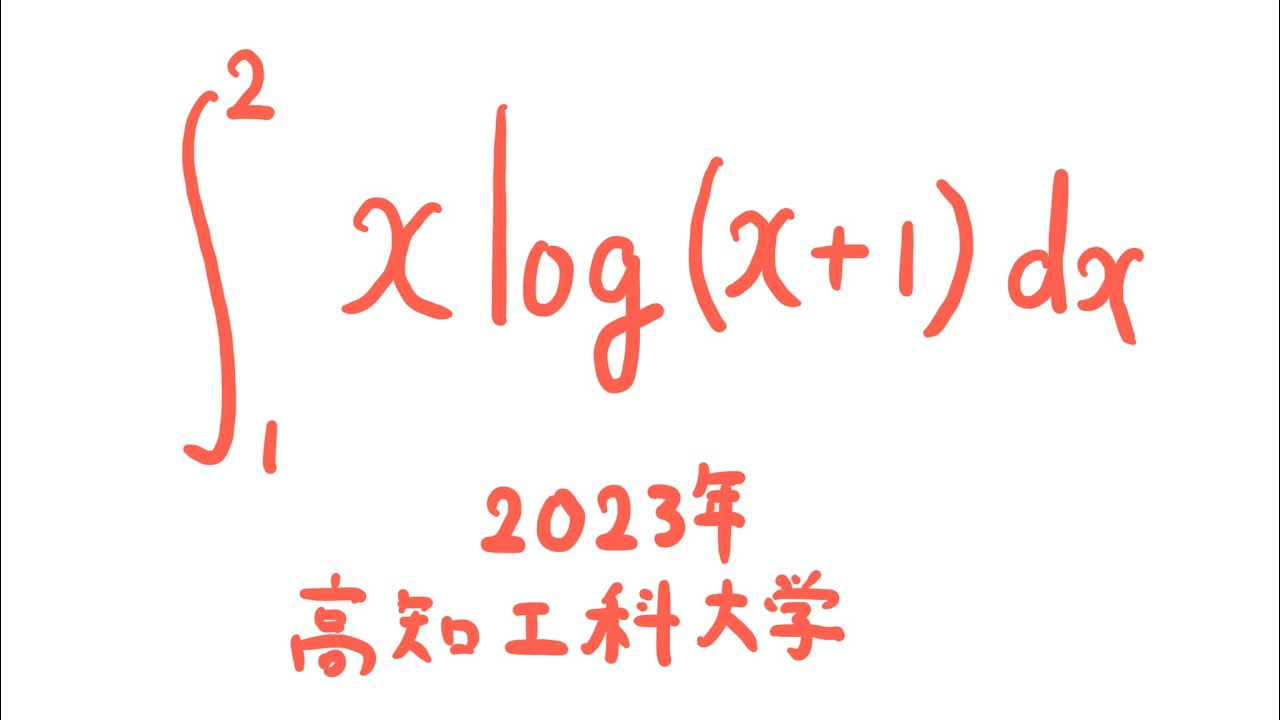
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#高知工科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{2} x\ log(x+1)dx$
出典：2023年高知工科大学
この動画を見る
$\displaystyle \int_{1}^{2} x\ log(x+1)dx$
出典：2023年高知工科大学
#高知工科大学(2022) #定積分 #Shorts
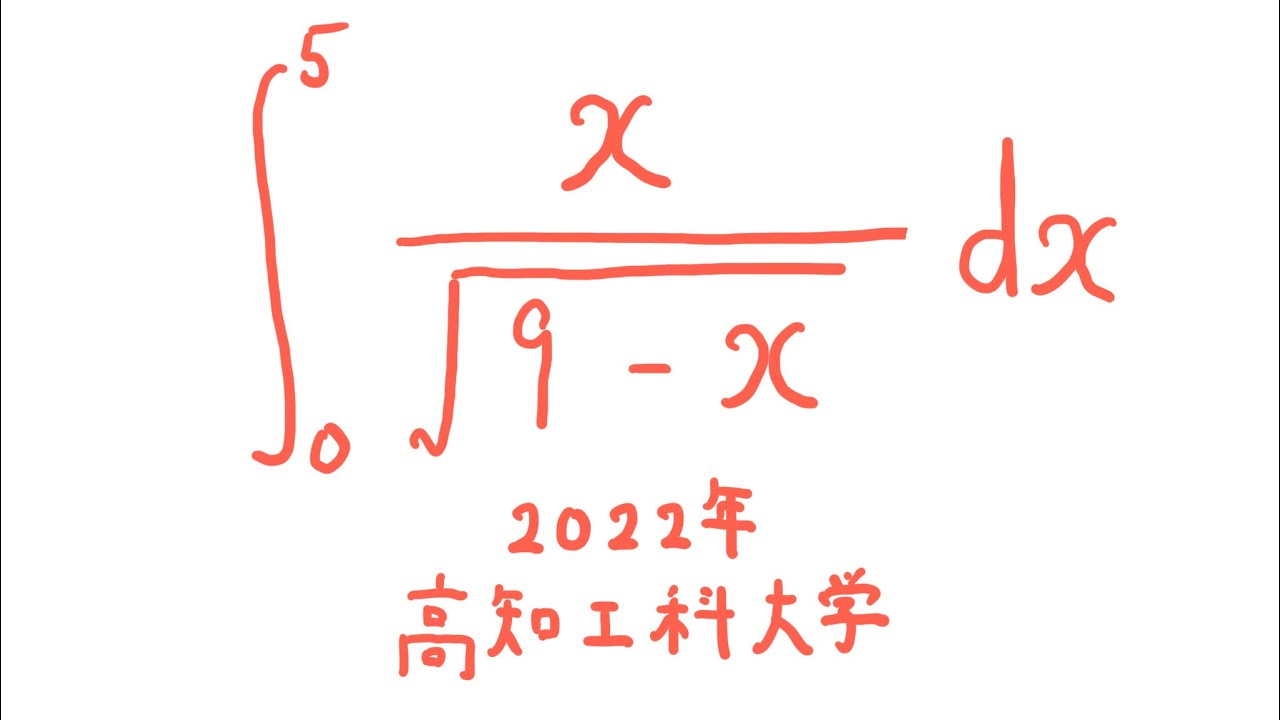
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#高知工科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{5} \displaystyle \frac{x}{\sqrt{ 9-x }} dx$
出典：2022年高知工科大学
この動画を見る
$\displaystyle \int_{0}^{5} \displaystyle \frac{x}{\sqrt{ 9-x }} dx$
出典：2022年高知工科大学
大学入試問題#516「ちょっとした公式で一撃！」 高知工科大学(2022) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#高知工科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{4}} \displaystyle \frac{dx}{\tan^2x\ \cos^2x}$
出典：2022年高知工科大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{4}} \displaystyle \frac{dx}{\tan^2x\ \cos^2x}$
出典：2022年高知工科大学 入試問題