熊本大学
熊本大学
【高校数学】毎日積分60日目~47都道府県制覇への道~【④熊本】【毎日17時投稿】
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#熊本大学#数学(高校生)#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
定積分$\displaystyle \int_1^{\sqrt{t}}4tx(1-tx^2)e^{-tx^2}logxdx$の値を$t$を用いて表せ。
【熊本大学 2023】
この動画を見る
定積分$\displaystyle \int_1^{\sqrt{t}}4tx(1-tx^2)e^{-tx^2}logxdx$の値を$t$を用いて表せ。
【熊本大学 2023】
熊本大（理）漸化式
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#熊本大学#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
一般項を求めよ
$a_1=\displaystyle \frac{1}{8}$
$(4n^2-1)(a_n-a_{n+1})＝8(n^2-1)a_na_{n+1}$
熊本大学理学部過去問
この動画を見る
一般項を求めよ
$a_1=\displaystyle \frac{1}{8}$
$(4n^2-1)(a_n-a_{n+1})＝8(n^2-1)a_na_{n+1}$
熊本大学理学部過去問
熊本大（文）漸化式
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#熊本大学#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
一般項を求めよ
$a_1=\displaystyle \frac{2}{3}$
$2(a_n-a_{n+1})=(n+2)a_na_{n+1}$
熊本大学文学部
この動画を見る
一般項を求めよ
$a_1=\displaystyle \frac{2}{3}$
$2(a_n-a_{n+1})=(n+2)a_na_{n+1}$
熊本大学文学部
数学「大学入試良問集」【17−2 Sn入り漸化式と極限】を宇宙一わかりやすく
単元：
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#熊本大学#数学(高校生)#数Ⅲ
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
数列$\{a_n\}$について、$S_n=\displaystyle \sum_{k=1}^n a_k$ $n=1,2,3,・・・,S_0=0$とおく。
$a_n=S_{n-1}+n・2^n$ $n=1,2,3,・・・$ が成り立つとき、次の各問いに答えよ。
（1）$S_n$を$n$の式で表せ。
（2）極限値$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\displaystyle \frac{2^k}{a_k}$を求めよ。
この動画を見る
数列$\{a_n\}$について、$S_n=\displaystyle \sum_{k=1}^n a_k$ $n=1,2,3,・・・,S_0=0$とおく。
$a_n=S_{n-1}+n・2^n$ $n=1,2,3,・・・$ が成り立つとき、次の各問いに答えよ。
（1）$S_n$を$n$の式で表せ。
（2）極限値$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\displaystyle \frac{2^k}{a_k}$を求めよ。
数学「大学入試良問集」【11−3 円と放物線（面積）】を宇宙一わかりやすく
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#熊本大学#数学(高校生)
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
点$A$を中心とする円$x^2+(y-a)^2=bb^2$が、放物線$y=x^2$と異なる2点$P,Q$で接している。
ただし、$a \gt \displaystyle \frac{1}{2}$とする。
次の各問いに答えよ。
（1）$a$と$b$の関係式を求めよ。
（2）$\triangle APQ$が正三角形のとき、円と放物線で囲まれた三日月形の面積を求めよ。
この動画を見る
点$A$を中心とする円$x^2+(y-a)^2=bb^2$が、放物線$y=x^2$と異なる2点$P,Q$で接している。
ただし、$a \gt \displaystyle \frac{1}{2}$とする。
次の各問いに答えよ。
（1）$a$と$b$の関係式を求めよ。
（2）$\triangle APQ$が正三角形のとき、円と放物線で囲まれた三日月形の面積を求めよ。
熊本大 漸化式
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#熊本大学#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$S_n=2a_n+n^2$
2通りの方法で一般項を求めよ
出典：熊本大学 過去問
この動画を見る
$S_n=2a_n+n^2$
2通りの方法で一般項を求めよ
出典：熊本大学 過去問
熊本大 関数の領域
単元：
#大学入試過去問(数学)#微分とその応用#色々な関数の導関数#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#熊本大学#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
y \geqq x^2-1 \\
y \leqq x+1
\end{array}
\right.
\end{eqnarray}$
$(x,y)$がこの領域を動く
$x^2+y^2-4y$の最大値・最小値を求めよ。
出典：2001年熊本大学 過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
y \geqq x^2-1 \\
y \leqq x+1
\end{array}
\right.
\end{eqnarray}$
$(x,y)$がこの領域を動く
$x^2+y^2-4y$の最大値・最小値を求めよ。
出典：2001年熊本大学 過去問
熊本大（医）整数・数列・二次関数
単元：
#数Ⅰ#数A#大学入試過去問(数学)#２次関数#整数の性質#数列#学校別大学入試過去問解説(数学)#熊本大学#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$7^n$の一の位を$a_n(n$自然数$)$
（1）
$a_{99}$
（2）
$-n^2+2na_n$の最大値とそのときの$n$
出典：1989年熊本大学医学部 過去問
この動画を見る
$7^n$の一の位を$a_n(n$自然数$)$
（1）
$a_{99}$
（2）
$-n^2+2na_n$の最大値とそのときの$n$
出典：1989年熊本大学医学部 過去問
熊本大 対数関数の最大値
単元：
#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#対数関数#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#熊本大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
次の関数の最大値
$f(x)=log_2 x+2log_2(6-x)$
$f(x)=log_2x+log_2(6-x)^2$
出典：熊本大学 過去問
この動画を見る
次の関数の最大値
$f(x)=log_2 x+2log_2(6-x)$
$f(x)=log_2x+log_2(6-x)^2$
出典：熊本大学 過去問
熊本大（医）連立漸化式 高校数学 Mathematics Japanese university entrance exam
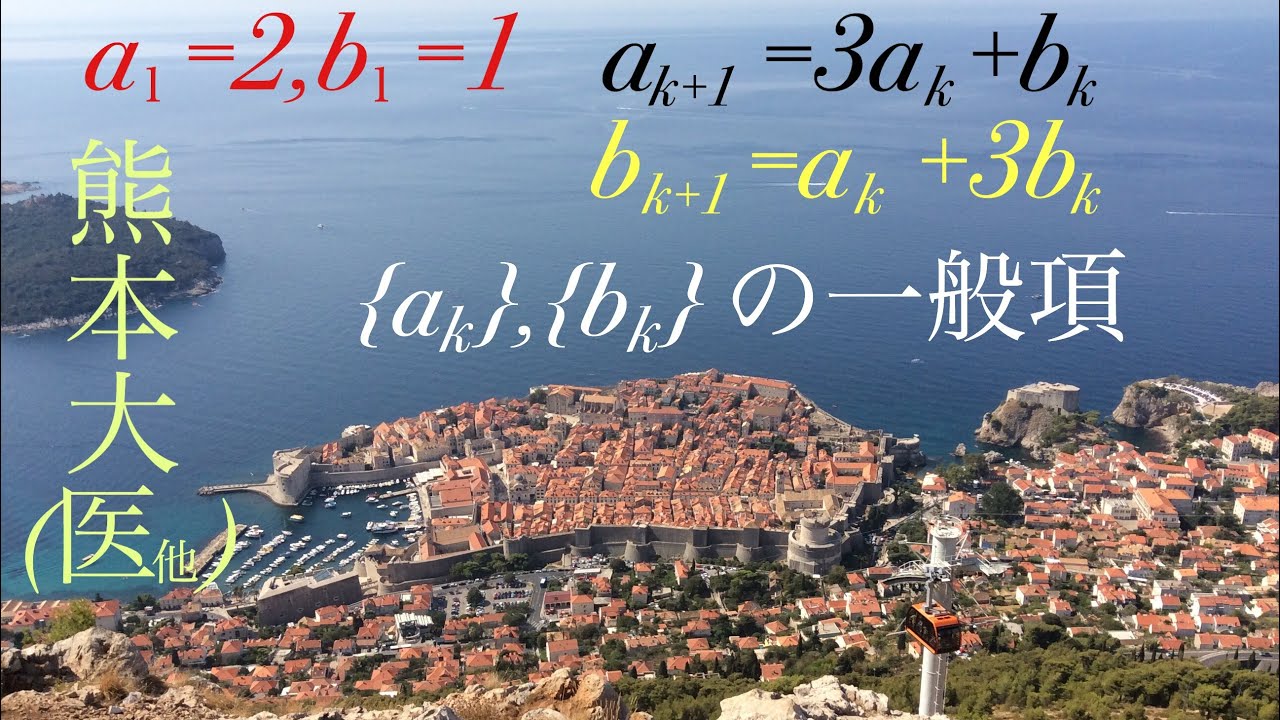
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#熊本大学#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a_{1}=2,b_{1}=1$
$a_{k+1}=3a_{k}+b_{k}$
$b_{k+1}=a_{k}+3b_{k}$
出典：熊本大学 過去問
この動画を見る
$a_{1}=2,b_{1}=1$
$a_{k+1}=3a_{k}+b_{k}$
$b_{k+1}=a_{k}+3b_{k}$
出典：熊本大学 過去問
上智大 熊本大 Mathematics Japanese university entrance exam
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#上智大学#熊本大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
上智大学過去問題
$x^{1000}$を$x^3+x^2+x+1$で割った余りと商の$x^{100}$の係数を求めよ。
熊本大学過去問題
$x^4+x^3+x^2+x+1$を実数係数のxの2次式の積で
この動画を見る
上智大学過去問題
$x^{1000}$を$x^3+x^2+x+1$で割った余りと商の$x^{100}$の係数を求めよ。
熊本大学過去問題
$x^4+x^3+x^2+x+1$を実数係数のxの2次式の積で
熊本大 漸化式 高校数学 Japanese university entrance exam questions
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#熊本大学#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
熊本大学過去問題
$a_1=b_1=1,b_{n+1}=3b_n+a_n$
$c_n=a_n+b_n+1$
数列｛$c_n$｝は公比3の等比数列である。
(1)$a_n$をnで表せ。
(2)$b_n$をnで表せ。
この動画を見る
熊本大学過去問題
$a_1=b_1=1,b_{n+1}=3b_n+a_n$
$c_n=a_n+b_n+1$
数列｛$c_n$｝は公比3の等比数列である。
(1)$a_n$をnで表せ。
(2)$b_n$をnで表せ。