奈良女子大学
奈良女子大学
奈良女子大 基本定理の証明
単元：
#奈良女子大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2022奈良女子大学過去問題
m,n整数
p,q,r実数(q$\neq$0)
$x^3+mx^2+nx+1=0$
はrとp+qiを解に持つ
(1)p-qiも解であることを示せ
(2)$r(p^2+q^2)=-1$を示せ
(3)|p+qi|= 1となる(m,n)をすべて求めよ
この動画を見る
2022奈良女子大学過去問題
m,n整数
p,q,r実数(q$\neq$0)
$x^3+mx^2+nx+1=0$
はrとp+qiを解に持つ
(1)p-qiも解であることを示せ
(2)$r(p^2+q^2)=-1$を示せ
(3)|p+qi|= 1となる(m,n)をすべて求めよ
奈良女子大 三次方程式の解
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#奈良女子大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x^3+mx^2+nx+1=0$は絶対値が1となる虚数解を持つ.
このとき整数(m,n)をすべて求めよ.
奈良女子大過去問
この動画を見る
$x^3+mx^2+nx+1=0$は絶対値が1となる虚数解を持つ.
このとき整数(m,n)をすべて求めよ.
奈良女子大過去問
奈良女子大 数列の積
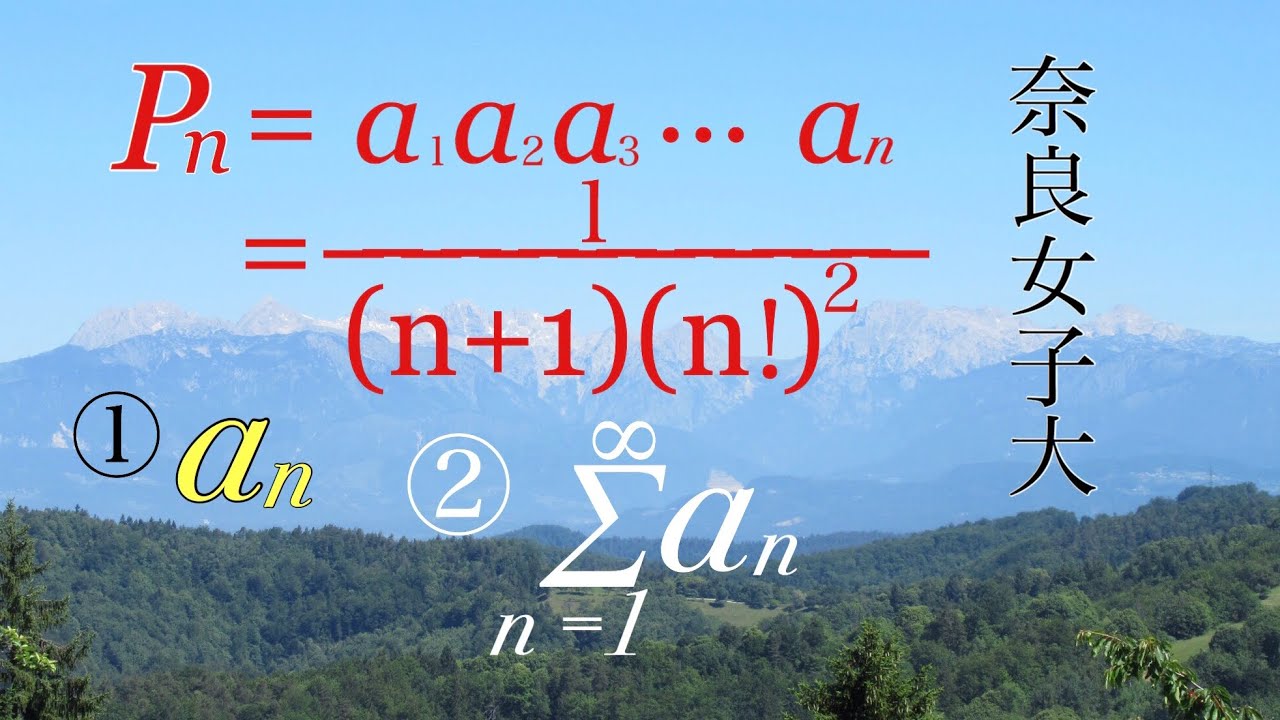
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#奈良女子大学#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$P_n=a_1a_2a_3…a_n=\displaystyle \frac{1}{(n+1)(n!)^2}$
（1）
$a_n$を求めよ
（2）
$\displaystyle \sum_{n=1}^\infty a_m$を求めよ
出典：奈良女子大学 過去問
この動画を見る
$P_n=a_1a_2a_3…a_n=\displaystyle \frac{1}{(n+1)(n!)^2}$
（1）
$a_n$を求めよ
（2）
$\displaystyle \sum_{n=1}^\infty a_m$を求めよ
出典：奈良女子大学 過去問
和歌山県立医大 奈良女子大 Mathematics Japanese university entrance exam
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#奈良女子大学#数学(高校生)#数B#和歌山県立医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
①$n^3(n^2-1)$が8の倍数であることを示せ($n$)整数
②$\displaystyle \sum_{k=1}^n \displaystyle \frac{1}{k(k+1)(k+2)(k+3)}$
出典：和歌山県立医科大学/奈良女子大学 過去問
この動画を見る
①$n^3(n^2-1)$が8の倍数であることを示せ($n$)整数
②$\displaystyle \sum_{k=1}^n \displaystyle \frac{1}{k(k+1)(k+2)(k+3)}$
出典：和歌山県立医科大学/奈良女子大学 過去問