 東京慈恵会医科大学
東京慈恵会医科大学
 東京慈恵会医科大学
東京慈恵会医科大学
福田の数学〜東京慈恵会医科大学2025医学部第4問〜複素数の絶対値の取りうる値の範囲

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
$z$は実数ではない複素数で、
$z+\dfrac{1}{z-1}$が正の実数となるものとする。
このとき、
$ \left \vert \dfrac{1}{z-1}-\dfrac{z- \overline{z}}{2}+1 \right \vert $がとりうる値の
範囲を求めよ。
ただし、$\overline{z}$は$z$に共役な複素数とする。
$2025$年東京慈恵会医科大学医学部過去問題
この動画を見る
$\boxed{4}$
$z$は実数ではない複素数で、
$z+\dfrac{1}{z-1}$が正の実数となるものとする。
このとき、
$ \left \vert \dfrac{1}{z-1}-\dfrac{z- \overline{z}}{2}+1 \right \vert $がとりうる値の
範囲を求めよ。
ただし、$\overline{z}$は$z$に共役な複素数とする。
$2025$年東京慈恵会医科大学医学部過去問題
福田の数学〜東京慈恵会医科大学2025医学部第3問〜双曲線が表す領域と素数の性質

単元:
#数A#大学入試過去問(数学)#平面上の曲線#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
自然数$p$は$2$以上の定数とする。
$xy$平面上で不等式$x^2-py^2 \geqq -1$の表す領域
を$D$とする。
自然数$r$は、円$(x-p)^2+y^2=r$が領域$D$に
含まれるような最大のものとするとき、
次の問いに答えよ。
(1)$r$を$p$を用いて表せ。
(2) (1)のもとで、関係式$(x-p)^2+y^2=r$をみたす
互いに異なる素数の組$(x,y,p)$のうち、
$p$の値が最小となるものを求めよ。
$2025$年東京慈恵会医科大学医学部過去問題
この動画を見る
$\boxed{3}$
自然数$p$は$2$以上の定数とする。
$xy$平面上で不等式$x^2-py^2 \geqq -1$の表す領域
を$D$とする。
自然数$r$は、円$(x-p)^2+y^2=r$が領域$D$に
含まれるような最大のものとするとき、
次の問いに答えよ。
(1)$r$を$p$を用いて表せ。
(2) (1)のもとで、関係式$(x-p)^2+y^2=r$をみたす
互いに異なる素数の組$(x,y,p)$のうち、
$p$の値が最小となるものを求めよ。
$2025$年東京慈恵会医科大学医学部過去問題
福田の数学〜東京慈恵会医科大学2025医学部第2問〜定積分と不等式の証明

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
次の問いに答えよ。ただし、対数は自然対数とする。
(1)$3$以上の自然数$n$について、
次の不等式が成り立つことを示せ。
$\dfrac{1}{2\log(n+1)}\leqq \displaystyle \int_{0}^{1} \dfrac{x}{\log(x+n)} dx \leqq \dfrac{1}{2\log n}$
(2)不定積分$\displaystyle \int \dfrac{1}{x(log x)^2} dx$ を求めよ。
(3)$m \geqq n$をみたす$3$以上の自然数$m,n$について、
次の不等式が成り立つことを示せ。
$\dfrac{1}{\log n}-\dfrac{1}{\log(m+1)}\leqq \displaystyle \sum_{k=n}^{m} \dfrac{2}{k \log k} \displaystyle \int_{0}^{1} \dfrac{1}{\log(x+k)} dx \leqq \dfrac{1}{\log(n-1)} -\dfrac{1}{\log m}$
$2025$年東京慈恵会医科大学医学部過去問題
この動画を見る
$\boxed{2}$
次の問いに答えよ。ただし、対数は自然対数とする。
(1)$3$以上の自然数$n$について、
次の不等式が成り立つことを示せ。
$\dfrac{1}{2\log(n+1)}\leqq \displaystyle \int_{0}^{1} \dfrac{x}{\log(x+n)} dx \leqq \dfrac{1}{2\log n}$
(2)不定積分$\displaystyle \int \dfrac{1}{x(log x)^2} dx$ を求めよ。
(3)$m \geqq n$をみたす$3$以上の自然数$m,n$について、
次の不等式が成り立つことを示せ。
$\dfrac{1}{\log n}-\dfrac{1}{\log(m+1)}\leqq \displaystyle \sum_{k=n}^{m} \dfrac{2}{k \log k} \displaystyle \int_{0}^{1} \dfrac{1}{\log(x+k)} dx \leqq \dfrac{1}{\log(n-1)} -\dfrac{1}{\log m}$
$2025$年東京慈恵会医科大学医学部過去問題
福田の数学〜東京慈恵会医科大学2025医学部第1問〜さいころの目の積の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
$1$個のさいころを$3$回続けて投げるとき、
$k$回目に出る目を$X_k (k-1,2,3)$とする。
このとき、
積$X_1 X_2 X_3$が$10$の倍数になる確率は$\boxed{ア}$、
和$X_1+X_2,X_2+X_3,X_3+X_1$が、
いずれも$6$の倍数にならない確率は$\boxed{イ}$である。
$2025$年東京慈恵会医科大学医学部過去問題
この動画を見る
$\boxed{1}$
$1$個のさいころを$3$回続けて投げるとき、
$k$回目に出る目を$X_k (k-1,2,3)$とする。
このとき、
積$X_1 X_2 X_3$が$10$の倍数になる確率は$\boxed{ア}$、
和$X_1+X_2,X_2+X_3,X_3+X_1$が、
いずれも$6$の倍数にならない確率は$\boxed{イ}$である。
$2025$年東京慈恵会医科大学医学部過去問題
福田の数学〜過去の入試問題(期間限定)〜東京慈恵会医科大学医学部2020第4問〜正四面体の切り口の面積の最小値

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
oを原点とするxyz 空間内に、xy平面上の放物線y=x²をy軸のまわりに回転してできる曲面Sと、正四面体OABCがあり、条件「3頂点A, B, CはS上にある」をみたしている。このとき、次の問いに答えよ。
(1)正四面体 OABCの1辺の長さを求めよ。
(2)正四面体 OABCが条件をみたしながら動くとき、xy平面による正四面体OABCの切り口の面積の最小値を求めよ。
この動画を見る
oを原点とするxyz 空間内に、xy平面上の放物線y=x²をy軸のまわりに回転してできる曲面Sと、正四面体OABCがあり、条件「3頂点A, B, CはS上にある」をみたしている。このとき、次の問いに答えよ。
(1)正四面体 OABCの1辺の長さを求めよ。
(2)正四面体 OABCが条件をみたしながら動くとき、xy平面による正四面体OABCの切り口の面積の最小値を求めよ。
福田の数学〜過去の入試問題(期間限定)〜東京慈恵会医科大学医学部2020第2問〜関数列の極限

単元:
#大学入試過去問(数学)#微分法と積分法#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京慈恵会医科大学#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$p$を$2$以上の自然数の定数とする。$n$=$2$, $3$, $4$...に対して、関数 $f_n(x) $$(n\gt0)$を
$f_n(x) = (1 + \dfrac{x}{n})(1 + \dfrac{x}{n+1}) \cdot\cdot \cdot(1 + \dfrac{x}{pn})
$
で定める。例えば$p$ = $2$のとき
$
f_2(x) = (1 + \dfrac{x}{2})(1 + \dfrac{x}{3})(1 + \dfrac{x}{4})
$
$
f_3(x) = (1 + \dfrac{x}{3})(1 + \dfrac{x}{4})(1 + \dfrac{x}{5})(1 + \dfrac{x}{6})
$
である。$f(x)=\displaystyle \lim_{ n \to \infty }f_n(x)$ $(n\gt0)$とおくとき、次の問に答えよ。
$(1)$$t$$\geqq$$0$のとき、不等式$\dfrac{t}{1+t}$$\leqq$$\log(1+t)$$\leqq$$t$ が成り立つことを示せ。ただし、対数は自然対数とする。
$(2)$ $f(x)$を求めよ。
この動画を見る
$p$を$2$以上の自然数の定数とする。$n$=$2$, $3$, $4$...に対して、関数 $f_n(x) $$(n\gt0)$を
$f_n(x) = (1 + \dfrac{x}{n})(1 + \dfrac{x}{n+1}) \cdot\cdot \cdot(1 + \dfrac{x}{pn})
$
で定める。例えば$p$ = $2$のとき
$
f_2(x) = (1 + \dfrac{x}{2})(1 + \dfrac{x}{3})(1 + \dfrac{x}{4})
$
$
f_3(x) = (1 + \dfrac{x}{3})(1 + \dfrac{x}{4})(1 + \dfrac{x}{5})(1 + \dfrac{x}{6})
$
である。$f(x)=\displaystyle \lim_{ n \to \infty }f_n(x)$ $(n\gt0)$とおくとき、次の問に答えよ。
$(1)$$t$$\geqq$$0$のとき、不等式$\dfrac{t}{1+t}$$\leqq$$\log(1+t)$$\leqq$$t$ が成り立つことを示せ。ただし、対数は自然対数とする。
$(2)$ $f(x)$を求めよ。
福田の数学〜過去の入試問題(期間限定)〜東京慈恵会医科大学医学部2020第2問〜関数列の極限

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\fbox{1}$ 次の$\square$にあてはまる適切な数値を解答欄に記入せよ。
袋$A$には赤玉$3$個、白玉$1$個、袋$B$には赤玉$1$個、白玉$3$個が入っている。
「袋$A$から$2$個の玉を取り出して袋$B$に入れ、次に袋$B$から$2$個の玉を取り出して袋$A$に入れる」という操作を繰り返す。$1$回の操作の後、袋$A$に白玉が$2$個以上ある確率は$\fbox{ア}$、$2$回の操作の後、袋$A$の中が白玉だけになる確率は$\fbox{イ}$である。
この動画を見る
$\fbox{1}$ 次の$\square$にあてはまる適切な数値を解答欄に記入せよ。
袋$A$には赤玉$3$個、白玉$1$個、袋$B$には赤玉$1$個、白玉$3$個が入っている。
「袋$A$から$2$個の玉を取り出して袋$B$に入れ、次に袋$B$から$2$個の玉を取り出して袋$A$に入れる」という操作を繰り返す。$1$回の操作の後、袋$A$に白玉が$2$個以上ある確率は$\fbox{ア}$、$2$回の操作の後、袋$A$の中が白玉だけになる確率は$\fbox{イ}$である。
福田の数学〜過去の入試問題(期間限定)〜東京慈恵会医科大学医学部2020第1問〜確率の基本性質

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\fbox{1}$ 次の$\square$にあてはまる適切な数値を解答欄に記入せよ。
袋$A$には赤玉$3$個、白玉$1$個、袋$B$には赤玉$1$個、白玉$3$個が入っている。
「袋$A$から$2$個の玉を取り出して袋$B$に入れ、次に袋$B$から$2$個の玉を取り出して袋$A$に入れる」という操作を繰り返す。$1$回の操作の後、袋$A$に白玉が$2$個以上ある確率は$\fbox{(ア)}$、$2$回の操作の後、袋$A$の中が白玉だけになる確率は$\fbox{(イ)}$である。
この動画を見る
$\fbox{1}$ 次の$\square$にあてはまる適切な数値を解答欄に記入せよ。
袋$A$には赤玉$3$個、白玉$1$個、袋$B$には赤玉$1$個、白玉$3$個が入っている。
「袋$A$から$2$個の玉を取り出して袋$B$に入れ、次に袋$B$から$2$個の玉を取り出して袋$A$に入れる」という操作を繰り返す。$1$回の操作の後、袋$A$に白玉が$2$個以上ある確率は$\fbox{(ア)}$、$2$回の操作の後、袋$A$の中が白玉だけになる確率は$\fbox{(イ)}$である。
福田の数学〜東京慈恵会医科大学2024医学部第4問〜円板を軸の周りに回転してできる立体の体積
単元:
#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
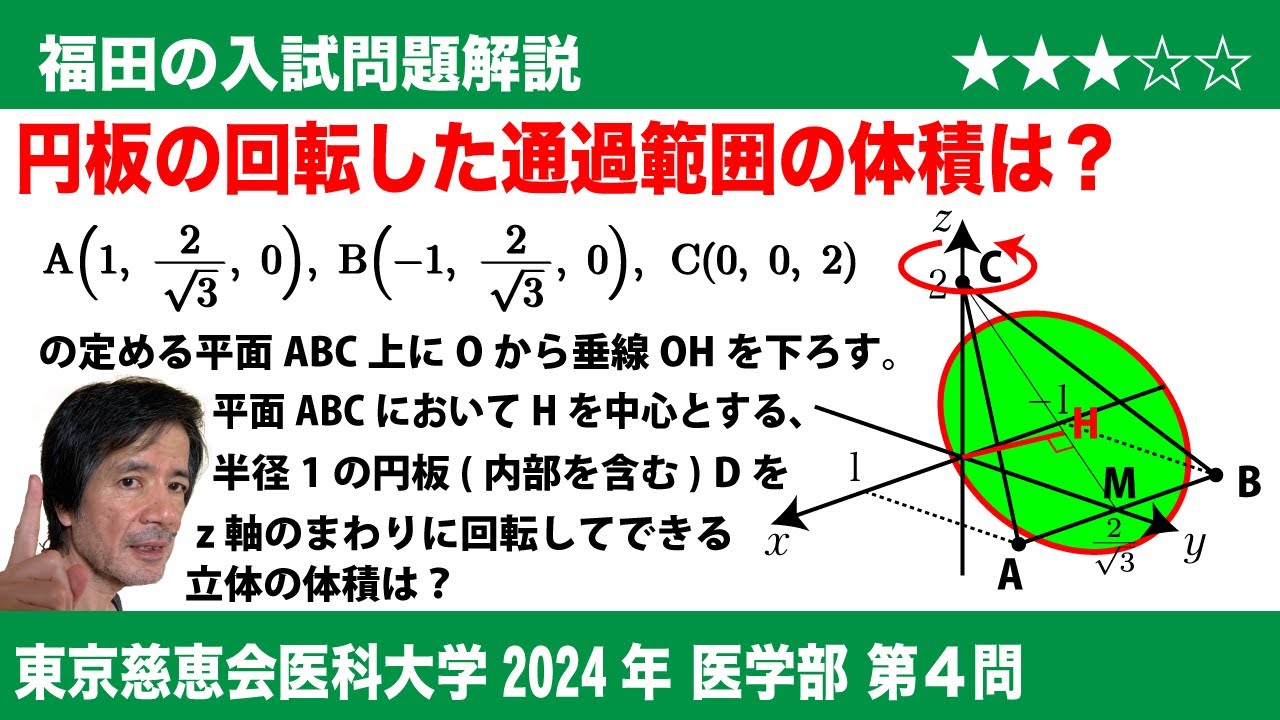
$\mathrm{O}$を原点とする$\mathrm{xyz} $平面において、3点 $\mathrm{A(1,\dfrac{2}{\sqrt{3}}, 0), B(-1, \dfrac{2}{\sqrt{3}}, 0), C(0, 0, 2)}$ の定める平面$\mathrm{ABC}$ 上に$\mathrm{O}$ から垂線$\mathrm{OH}$ を下ろす。平面$\mathrm{ABC}$ において、$\mathrm{H}$ を中心とする半径$\mathrm{1}$の円板(内部を含む)$\mathrm{D}$ を考える。
(1)平面$\mathrm{z = t}$ が$\mathrm{D}$と交わるような$\mathrm{t}$の範囲を求めよ。
(2)$\mathrm{D}$を$\mathrm{z}$軸の周りに$\mathrm{1}$回転させるとき、$\mathrm{D}$が通過してできる立体$\mathrm{K}$の体積$\mathrm{V}$を求めよ。
この動画を見る
$\mathrm{O}$を原点とする$\mathrm{xyz} $平面において、3点 $\mathrm{A(1,\dfrac{2}{\sqrt{3}}, 0), B(-1, \dfrac{2}{\sqrt{3}}, 0), C(0, 0, 2)}$ の定める平面$\mathrm{ABC}$ 上に$\mathrm{O}$ から垂線$\mathrm{OH}$ を下ろす。平面$\mathrm{ABC}$ において、$\mathrm{H}$ を中心とする半径$\mathrm{1}$の円板(内部を含む)$\mathrm{D}$ を考える。
(1)平面$\mathrm{z = t}$ が$\mathrm{D}$と交わるような$\mathrm{t}$の範囲を求めよ。
(2)$\mathrm{D}$を$\mathrm{z}$軸の周りに$\mathrm{1}$回転させるとき、$\mathrm{D}$が通過してできる立体$\mathrm{K}$の体積$\mathrm{V}$を求めよ。
福田の数学〜東京慈恵会医科大学2024医学部第3問〜条件を満たす2次式に関する証明と反例の作成

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$p$,$q$は互いに素である自然数とする。実数$a$,$b$,$c$に対して、$x$の2次多項式 $f(x)=ax^{ 2 }+bx+c$を考える。 ただし、$a \neq 0$とする。$f(x)$が条件「ある整数$k$について$f(k-1)$, $f(k)$, $f(k + 1)$ は整数となり、$f(x)$は $px-q$で割り切れる」をみたすとき、次の問いに答えよ。
(1) $\frac{2a}{p}$,$\frac{2c}{q}$は整数であることを示せ。
(2) 命題「$f(x)$が上の条件をみたすならば、$\frac{a}{p}$,$\frac{c}{q}$は整数である」は正しいか。正しければそれを示せ。正しくなければ、反例を1つあげよ。
この動画を見る
$p$,$q$は互いに素である自然数とする。実数$a$,$b$,$c$に対して、$x$の2次多項式 $f(x)=ax^{ 2 }+bx+c$を考える。 ただし、$a \neq 0$とする。$f(x)$が条件「ある整数$k$について$f(k-1)$, $f(k)$, $f(k + 1)$ は整数となり、$f(x)$は $px-q$で割り切れる」をみたすとき、次の問いに答えよ。
(1) $\frac{2a}{p}$,$\frac{2c}{q}$は整数であることを示せ。
(2) 命題「$f(x)$が上の条件をみたすならば、$\frac{a}{p}$,$\frac{c}{q}$は整数である」は正しいか。正しければそれを示せ。正しくなければ、反例を1つあげよ。
福田の数学〜東京慈恵会医科大学2024医学部第2問〜定積分で表された関数の最小値
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
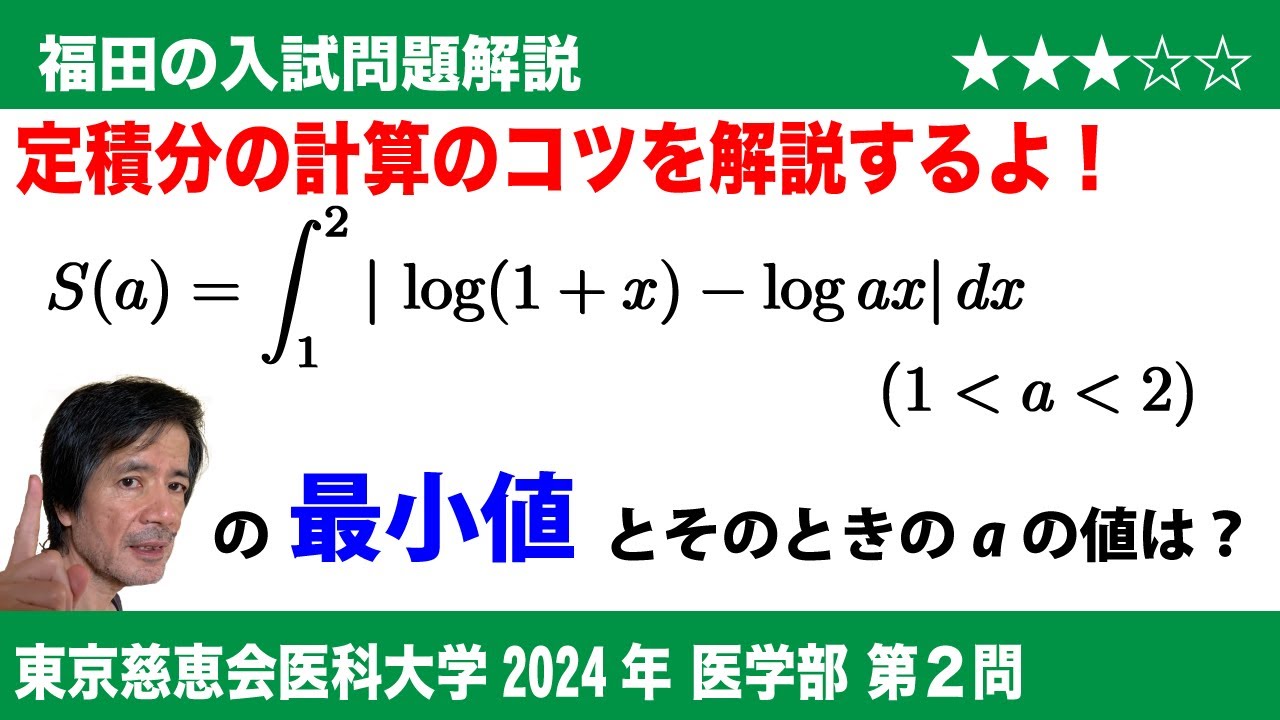
$\boxed{ 2 }1\lt a \lt 2$を満たす実数$a$について、$S(a)=\int_1^2 {|log(1+x)-logax|} dx$とするとき、次の問いに答えよ。ただし、logは自然対数である。
(1)$a$の値に応じて、$1\leqq x \leqq 2$の範囲で方程式$log(1+x)-logax=0$の解の個数を調べよ。
(2)$S(a)$を求めよ。
(3)$S(a)(1 \lt a \lt 2)$の最小値と、そのときの$a$の値を求めよ。
この動画を見る
$\boxed{ 2 }1\lt a \lt 2$を満たす実数$a$について、$S(a)=\int_1^2 {|log(1+x)-logax|} dx$とするとき、次の問いに答えよ。ただし、logは自然対数である。
(1)$a$の値に応じて、$1\leqq x \leqq 2$の範囲で方程式$log(1+x)-logax=0$の解の個数を調べよ。
(2)$S(a)$を求めよ。
(3)$S(a)(1 \lt a \lt 2)$の最小値と、そのときの$a$の値を求めよ。
福田の数学〜東京慈恵会医科大学2024医学部第1問〜条件付き確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{ 1 }$1から3までの番号をつけた赤玉3個と、1から3までの番号をつけた白玉3個が入った袋から、玉を1個ずつ3回取り出し、玉に書かれた番号を取り出した順に$a_1,a_2,a_3$とする。ただし、取り出した玉はもとに戻さないものとする。
取り出した3個の玉が、赤玉2個、白玉1個であったとき、
$a_1 \lt a_2 \lt a_3$となる条件付き確率は$\boxed{ア}$、
$a_1 \lt a_2$かつ$a_2 \gt a_3$となる条件付き確率は$\boxed{イ}$
である。
この動画を見る
$\boxed{ 1 }$1から3までの番号をつけた赤玉3個と、1から3までの番号をつけた白玉3個が入った袋から、玉を1個ずつ3回取り出し、玉に書かれた番号を取り出した順に$a_1,a_2,a_3$とする。ただし、取り出した玉はもとに戻さないものとする。
取り出した3個の玉が、赤玉2個、白玉1個であったとき、
$a_1 \lt a_2 \lt a_3$となる条件付き確率は$\boxed{ア}$、
$a_1 \lt a_2$かつ$a_2 \gt a_3$となる条件付き確率は$\boxed{イ}$
である。
大学入試問題#731「手を動かす前に読みをいれる」 東京慈恵会医科大学(2004) 定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学#東京慈恵会医科大学
指導講師:
ますただ
問題文全文(内容文):
$\theta$は$0 \lt \theta \lt \displaystyle \frac{\pi}{2}$かつ$\tan\theta=2$を満たすとする。
$\displaystyle \int_{\frac{\pi}{4}}^{\theta} \displaystyle \frac{dx}{\sin^4x}$
出典:2004年東京慈恵医科大学 入試問題
この動画を見る
$\theta$は$0 \lt \theta \lt \displaystyle \frac{\pi}{2}$かつ$\tan\theta=2$を満たすとする。
$\displaystyle \int_{\frac{\pi}{4}}^{\theta} \displaystyle \frac{dx}{\sin^4x}$
出典:2004年東京慈恵医科大学 入試問題
大学入試問題#673「何度も解いてるはず」 東京慈恵会医科大学(2001)

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学#東京慈恵会医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} log(x^2+3) dx$
出典:2001年東京慈恵会医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} log(x^2+3) dx$
出典:2001年東京慈恵会医科大学 入試問題
福田の数学〜東京慈恵会医科大学2023年医学部第4問〜ベクトル方程式と関数の増減

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#数C#数Ⅲ#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ Oを原点とする座標空間に2点A(0,0,1), B(0,0,-1)がある。r>0, -π≦θ<πに対して、2点P(r$\cos\theta$,r$\sin\theta$,0),Q($\frac{1}{r}\cos\theta$,$\frac{1}{r}\sin\theta$,0)をとり、2直線APとBQの交点をR(a,b,c)とするとき、次の問いに答えよ。
(1)a,b,cの間に成り立つ関係式を求めよ。
(2)点G(4,1,1)をとる。r,θがr$\cos\theta$=$\frac{1}{2}$を満たしながら変化するとき、内積$\overrightarrow{OG}・\overrightarrow{OR}$の最大値とそのときのa,b,cの値を求めよ。
2023東京慈恵会医科大学医学部過去問
この動画を見る
$\Large\boxed{4}$ Oを原点とする座標空間に2点A(0,0,1), B(0,0,-1)がある。r>0, -π≦θ<πに対して、2点P(r$\cos\theta$,r$\sin\theta$,0),Q($\frac{1}{r}\cos\theta$,$\frac{1}{r}\sin\theta$,0)をとり、2直線APとBQの交点をR(a,b,c)とするとき、次の問いに答えよ。
(1)a,b,cの間に成り立つ関係式を求めよ。
(2)点G(4,1,1)をとる。r,θがr$\cos\theta$=$\frac{1}{2}$を満たしながら変化するとき、内積$\overrightarrow{OG}・\overrightarrow{OR}$の最大値とそのときのa,b,cの値を求めよ。
2023東京慈恵会医科大学医学部過去問
福田の数学〜東京慈恵会医科大学2023年医学部第3問〜無理数である証明

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ Oを原点とする座標平面において、第1象限に属する点P($\sqrt 2r$, $\sqrt 3s$)(r,sは有理数)をとるとき、線分OPの長さは無理数となることを示せ。
2023東京慈恵会医科大学医学部過去問
この動画を見る
$\Large\boxed{3}$ Oを原点とする座標平面において、第1象限に属する点P($\sqrt 2r$, $\sqrt 3s$)(r,sは有理数)をとるとき、線分OPの長さは無理数となることを示せ。
2023東京慈恵会医科大学医学部過去問
福田の数学〜東京慈恵会医科大学2023年医学部第2問〜定積分で表された関数と極限

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ nを自然数、aを正の定数とする。関数f(x)は等式
$f(x)=x+\displaystyle\frac{1}{n}\int_0^xf(t)dt$
を満たし、関数g(x)は$g(x)$=$ae^{-\frac{x}{n}}+a$とする。2つの曲線y=f(x)とy=g(x)はある1点を共有し、その点における2つの接線が直交するとき、次の問いに答えよ。ただし、eは自然対数の底とする。
(1)h(x)=$e^{-\frac{x}{n}}f(x)$とおくとき、導関数h'(x)とh(x)を求めよ。
(2)aをnを用いて表せ。
(3)2つの曲線y=f(x), y=g(x)とy軸で囲まれた部分の面積を$S_n$とするとき、
極限値$\displaystyle\lim_{n \to \infty}\frac{S_1+S_2+\cdots+S_n}{n^3}$ を求めよ。
2023東京慈恵会医科大学医学部過去問
この動画を見る
$\Large\boxed{2}$ nを自然数、aを正の定数とする。関数f(x)は等式
$f(x)=x+\displaystyle\frac{1}{n}\int_0^xf(t)dt$
を満たし、関数g(x)は$g(x)$=$ae^{-\frac{x}{n}}+a$とする。2つの曲線y=f(x)とy=g(x)はある1点を共有し、その点における2つの接線が直交するとき、次の問いに答えよ。ただし、eは自然対数の底とする。
(1)h(x)=$e^{-\frac{x}{n}}f(x)$とおくとき、導関数h'(x)とh(x)を求めよ。
(2)aをnを用いて表せ。
(3)2つの曲線y=f(x), y=g(x)とy軸で囲まれた部分の面積を$S_n$とするとき、
極限値$\displaystyle\lim_{n \to \infty}\frac{S_1+S_2+\cdots+S_n}{n^3}$ を求めよ。
2023東京慈恵会医科大学医学部過去問
福田の数学〜東京慈恵会医科大学2023年医学部第1問〜整数解と確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#整数の性質#確率#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 袋の中に1から5までの番号をつけた5個の玉が入っている。この袋から玉を1個取り出し、番号を調べてから元に戻す試行を、4回続けて行う。n回目(1≦n≦4)に取り出された玉の番号を$r_n$とするとき、
・$r_1$+$r_2$+$r_3$+$r_4$≦8 となる確率は$\boxed{\ \ (ア)\ \ }$
・$\displaystyle\frac{4}{r_1r_2}$+$\displaystyle\frac{2}{r_3r_4}$=1となる確率は$\boxed{\ \ (イ)\ \ }$
である。
2023東京慈恵会医科大学医学部過去問
この動画を見る
$\Large\boxed{1}$ 袋の中に1から5までの番号をつけた5個の玉が入っている。この袋から玉を1個取り出し、番号を調べてから元に戻す試行を、4回続けて行う。n回目(1≦n≦4)に取り出された玉の番号を$r_n$とするとき、
・$r_1$+$r_2$+$r_3$+$r_4$≦8 となる確率は$\boxed{\ \ (ア)\ \ }$
・$\displaystyle\frac{4}{r_1r_2}$+$\displaystyle\frac{2}{r_3r_4}$=1となる確率は$\boxed{\ \ (イ)\ \ }$
である。
2023東京慈恵会医科大学医学部過去問
慈恵医大 座標のフリした整数問題

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学#東京慈恵会医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
Oを原点とする座標平面において,第一象限に属する点P$(\sqrt2 r,\sqrt3 s)$(r,sは有理数)をとるとき,線分OPの長さは無理数となることを示せ.
慈恵医大過去問
この動画を見る
Oを原点とする座標平面において,第一象限に属する点P$(\sqrt2 r,\sqrt3 s)$(r,sは有理数)をとるとき,線分OPの長さは無理数となることを示せ.
慈恵医大過去問
慈恵医大 複素数の基本問題

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京慈恵会医科大学#東京慈恵会医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha=\cos\dfrac{2}{7}\pi+i\sin\dfrac{2}{7}\pi$
(1)$\alpha^7,\displaystyle \sum_{k=0}^6 {\alpha}_{k}$の値を求めよ.
(2)$\beta=\alpha^3+\alpha^5+\alpha^6$とするとき,$\beta+\bar{\beta},\beta\bar{\beta}$の値を求めよ.
(3)$\beta=a+bi,b$の正負を判定し$a,b$の値を求めよ.
慈恵医大過去問
この動画を見る
$\alpha=\cos\dfrac{2}{7}\pi+i\sin\dfrac{2}{7}\pi$
(1)$\alpha^7,\displaystyle \sum_{k=0}^6 {\alpha}_{k}$の値を求めよ.
(2)$\beta=\alpha^3+\alpha^5+\alpha^6$とするとき,$\beta+\bar{\beta},\beta\bar{\beta}$の値を求めよ.
(3)$\beta=a+bi,b$の正負を判定し$a,b$の値を求めよ.
慈恵医大過去問
福田の1.5倍速演習〜合格する重要問題052〜東京慈恵会医科大学2019年度医学部第2問〜2曲線の相接と囲まれた部分の面積とその極限

単元:
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京慈恵会医科大学#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ $a,b$は定数で$a \gt 1$とする。2つの曲線$C_1:y=\displaystyle\frac{3e^x-1}{e^x+1}$,$C_2:y=\displaystyle\frac{e^x}{a^2}+b$が共有点Pをもち、点Pにおいて共通の接線をもつとする。このとき、次の問いに答えよ。
(1)$C_1$の凹凸および変曲点を調べ、$C_1$の概形を描け。
(2)点Pの座標と$b$を$a$で表せ。
(3)$C_1$,$C_2$と$y$軸で囲まれた部分の面積$S(a)$を$a$で表せ。また、極限値$\displaystyle\lim_{a \to \infty}S(a)$を求めよ。
ただし、必要ならば$\displaystyle\lim_{x \to \infty}\frac{\log x}{x}= 0$であることを用いてよい。
2019東京慈恵会医科大学医学部過去問
この動画を見る
$\Large{\boxed{2}}$ $a,b$は定数で$a \gt 1$とする。2つの曲線$C_1:y=\displaystyle\frac{3e^x-1}{e^x+1}$,$C_2:y=\displaystyle\frac{e^x}{a^2}+b$が共有点Pをもち、点Pにおいて共通の接線をもつとする。このとき、次の問いに答えよ。
(1)$C_1$の凹凸および変曲点を調べ、$C_1$の概形を描け。
(2)点Pの座標と$b$を$a$で表せ。
(3)$C_1$,$C_2$と$y$軸で囲まれた部分の面積$S(a)$を$a$で表せ。また、極限値$\displaystyle\lim_{a \to \infty}S(a)$を求めよ。
ただし、必要ならば$\displaystyle\lim_{x \to \infty}\frac{\log x}{x}= 0$であることを用いてよい。
2019東京慈恵会医科大学医学部過去問
福田の数学〜東京慈恵会医科大学2022年医学部第2問〜微分可能性と最大値と体積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#微分とその応用#積分とその応用#微分法#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
実数aは正の定数とする。実数全体で定義された関数$f(x)=\frac{|x+a|}{\sqrt{x^2+1}}$について、
次の問いに答えよ。
(1)$f(x)$が$x=-a$で微分可能であるかどうか調べよ。
(2)$f(x)$の最大値が$\sqrt2$となるように、定数aの値を定めよ。
(3)定数aは(2)で定めた値とする。$y=f(x)$のグラフとx軸およびy軸で囲まれた部分
をx軸の周りに1回転させてできる立体の体積Vを求めよ。
2022東京慈恵会医科大学医学部過去問
この動画を見る
実数aは正の定数とする。実数全体で定義された関数$f(x)=\frac{|x+a|}{\sqrt{x^2+1}}$について、
次の問いに答えよ。
(1)$f(x)$が$x=-a$で微分可能であるかどうか調べよ。
(2)$f(x)$の最大値が$\sqrt2$となるように、定数aの値を定めよ。
(3)定数aは(2)で定めた値とする。$y=f(x)$のグラフとx軸およびy軸で囲まれた部分
をx軸の周りに1回転させてできる立体の体積Vを求めよ。
2022東京慈恵会医科大学医学部過去問
福田の数学〜東京慈恵会医科大学2022年医学部第1問〜確率の基本性質

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
袋Aには白玉2個、赤玉1個、袋Bには白玉1個、赤玉2個が入っている。
この状態から始めて、次の操作を繰り返し行う。
操作
① 袋A、袋Bから玉を1個ずつ取り出す。
② $(\textrm{i})$取り出した2個の玉の色が同じである場合は、取り出した玉を2個とも
袋Aに入れる。
$(\textrm{ii})$取り出した2個の玉の色が異なる場合は、袋Aから取り出した玉は袋B
に入れ、袋Bから取り出した玉は袋Aに入れる。
このとき、
・操作を2回繰り返した後に袋Aに入っている赤玉の個数が1個である確率は$\boxed{\ \ (ア)\ \ }$
・操作を3回繰り返した後に袋Aに入っている赤玉の個数が0個である確率は$\boxed{\ \ (イ)\ \ }$
である。
2022東京慈恵会医科大学医学部過去問
この動画を見る
袋Aには白玉2個、赤玉1個、袋Bには白玉1個、赤玉2個が入っている。
この状態から始めて、次の操作を繰り返し行う。
操作
① 袋A、袋Bから玉を1個ずつ取り出す。
② $(\textrm{i})$取り出した2個の玉の色が同じである場合は、取り出した玉を2個とも
袋Aに入れる。
$(\textrm{ii})$取り出した2個の玉の色が異なる場合は、袋Aから取り出した玉は袋B
に入れ、袋Bから取り出した玉は袋Aに入れる。
このとき、
・操作を2回繰り返した後に袋Aに入っている赤玉の個数が1個である確率は$\boxed{\ \ (ア)\ \ }$
・操作を3回繰り返した後に袋Aに入っている赤玉の個数が0個である確率は$\boxed{\ \ (イ)\ \ }$
である。
2022東京慈恵会医科大学医学部過去問
慈恵医大 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数$P$は素数、$a,b,c$自然数
$a$は素数
$a(ab-p^2)=C^2,b \leqq 2C$を満たす
(1)
$(a,b,c)$の組の個数を$P$を用いて表せ
(2)
$a,b,c$の最大公約数1となるような$(a,b,c)$の組の個数を$P$で表せ
出典:2017年東京慈恵会医科大学附属病院 過去問
この動画を見る
実数$P$は素数、$a,b,c$自然数
$a$は素数
$a(ab-p^2)=C^2,b \leqq 2C$を満たす
(1)
$(a,b,c)$の組の個数を$P$を用いて表せ
(2)
$a,b,c$の最大公約数1となるような$(a,b,c)$の組の個数を$P$で表せ
出典:2017年東京慈恵会医科大学附属病院 過去問
慈恵医大 複素数 3次方程式 有理数解の有無 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\theta=\displaystyle \frac{2}{9}\pi, \alpha=\cos \theta+i \sin \theta$
$\beta=\alpha+\alpha^8$
(1)
$\beta$は実数であることを示せ
(2)
$\beta$は整数係数の三次方程式の解である。
その方程式を求めよ。
(3)
(2)で求めた方程式は有理数の解をもたないことを示せ。
出典:2004年東京慈恵会医科大学 過去問
この動画を見る
$\theta=\displaystyle \frac{2}{9}\pi, \alpha=\cos \theta+i \sin \theta$
$\beta=\alpha+\alpha^8$
(1)
$\beta$は実数であることを示せ
(2)
$\beta$は整数係数の三次方程式の解である。
その方程式を求めよ。
(3)
(2)で求めた方程式は有理数の解をもたないことを示せ。
出典:2004年東京慈恵会医科大学 過去問
