東京都立大学
東京都立大学
東京都立大学 2023年 #定積分1 #Shorts
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京都立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{2\pi} \theta^2\sin\theta\ d\theta$
出典：2023年東京都立大学
この動画を見る
$\displaystyle \int_{0}^{2\pi} \theta^2\sin\theta\ d\theta$
出典：2023年東京都立大学
東京都立大学 2023年 #定積分 #Shorts
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京都立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{2\pi} 2\theta\ \sin^2\theta\ d\theta$
出典：2023年東京都立大学
この動画を見る
$\displaystyle \int_{0}^{2\pi} 2\theta\ \sin^2\theta\ d\theta$
出典：2023年東京都立大学
数学「大学入試良問集」【12−6 放物線と接線で囲まれた面積】を宇宙一わかりやすく
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#東京都立大学
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
$y=x^2$のグラフを$r$とする。
$b \lt a^2$をみたす点$P(a,b)$から$r$へ接線を2本引き、接点を$A,B$とする。
$r$と2本の線分$PA,PB$で囲まれた図形の面積が$\displaystyle \frac{2}{3}$になるような点$P$の軌跡を求めよ。
この動画を見る
$y=x^2$のグラフを$r$とする。
$b \lt a^2$をみたす点$P(a,b)$から$r$へ接線を2本引き、接点を$A,B$とする。
$r$と2本の線分$PA,PB$で囲まれた図形の面積が$\displaystyle \frac{2}{3}$になるような点$P$の軌跡を求めよ。
東京都立大 複素数
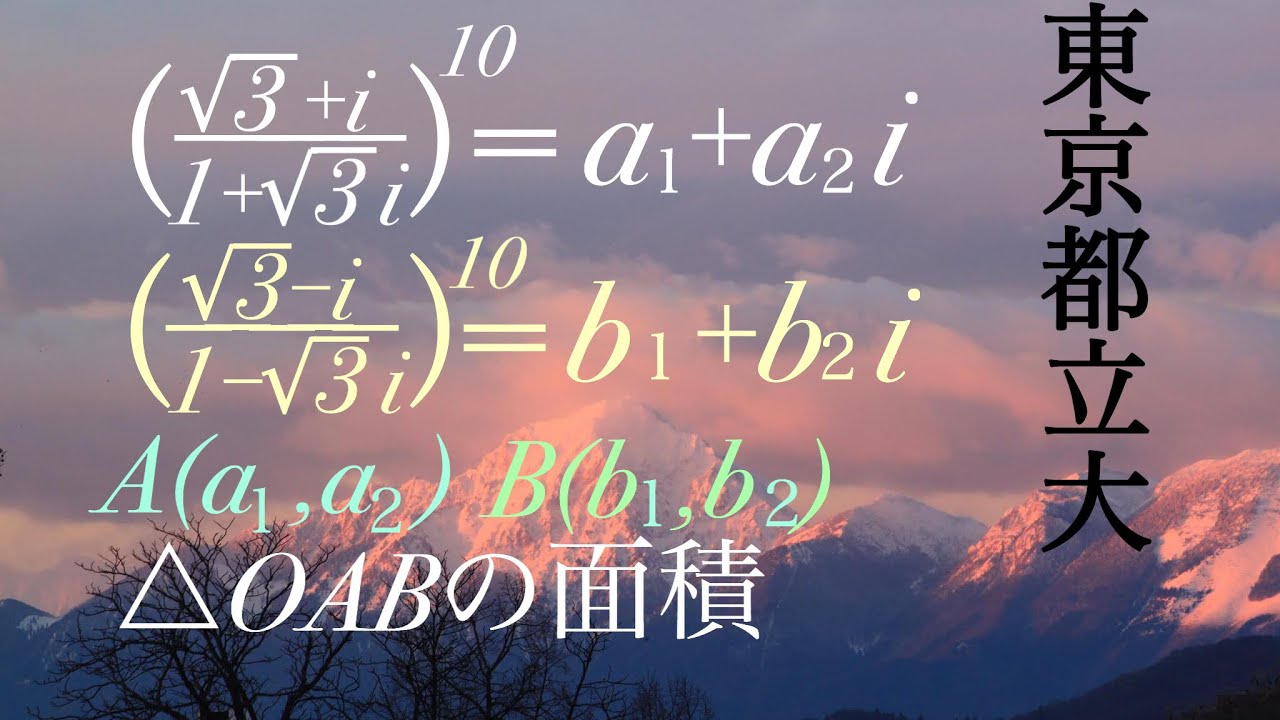
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#東京都立大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(\displaystyle \frac{\sqrt{ 3 }+i}{1+\sqrt{ 3 }i})^{10}=a_1+a_2i$
$(\displaystyle \frac{\sqrt{ 3 }-i}{1-\sqrt{ 3 }i})^{10}=b_1+b_2i$
（1）
$a_1,a_2,b_1,b_2$を求めよ
（2）
$A(a_1,a_2)$ $B(b_1,b_2)$
$\triangle OAB$の面積を求めよ
出典：2001年東京都立大学 過去問
この動画を見る
$(\displaystyle \frac{\sqrt{ 3 }+i}{1+\sqrt{ 3 }i})^{10}=a_1+a_2i$
$(\displaystyle \frac{\sqrt{ 3 }-i}{1-\sqrt{ 3 }i})^{10}=b_1+b_2i$
（1）
$a_1,a_2,b_1,b_2$を求めよ
（2）
$A(a_1,a_2)$ $B(b_1,b_2)$
$\triangle OAB$の面積を求めよ
出典：2001年東京都立大学 過去問
東京都立大
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#東京都立大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$z^4-2(\cos\displaystyle \frac{3}{7}\pi)z^3+2z^2-2(\cos\displaystyle \frac{3}{7}\pi)z+1=0$
（1）
$z+\displaystyle \frac{1}{z}$の値を求めよ
（2）
$z^n+\displaystyle \frac{1}{z^n}$の実部の最大値とそれを与える自然数$n$を求めよ
出典：東京都立大学 過去問
この動画を見る
$z^4-2(\cos\displaystyle \frac{3}{7}\pi)z^3+2z^2-2(\cos\displaystyle \frac{3}{7}\pi)z+1=0$
（1）
$z+\displaystyle \frac{1}{z}$の値を求めよ
（2）
$z^n+\displaystyle \frac{1}{z^n}$の実部の最大値とそれを与える自然数$n$を求めよ
出典：東京都立大学 過去問