2次関数とグラフ
2次関数とグラフ
福田の一夜漬け数学〜２次関数・解の存在範囲(1)〜高校1年生
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#2次関数とグラフ#解と判別式・解と係数の関係#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}} x^2-2mx-m+2=0$ が次のような解をもつとき、定数$m$の
値の範囲を求めよ。
(1)異なる2つの正の解
(2)異なる2つの負の解
(3)異符号の解
(4)2つの0以上の解
(5)2つの0以下の解
この動画を見る
${\Large\boxed{1}} x^2-2mx-m+2=0$ が次のような解をもつとき、定数$m$の
値の範囲を求めよ。
(1)異なる2つの正の解
(2)異なる2つの負の解
(3)異符号の解
(4)2つの0以上の解
(5)2つの0以下の解
福田の一夜漬け数学〜２次関数・２次不等式(2)絶対不等式〜高校1年生
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
① 任意の実数xに対して、不等式$ax^2-2\sqrt3x+a+2 \leqq 0$が成り立つ
ような定数aの範囲を求めよ。
②$0 \leqq x \leqq 8$の全てのxの値に対して、不等式$x^2-2mx+m+6 \gt 0$が
成り立つような定数mの値の範囲を求めよ。
この動画を見る
① 任意の実数xに対して、不等式$ax^2-2\sqrt3x+a+2 \leqq 0$が成り立つ
ような定数aの範囲を求めよ。
②$0 \leqq x \leqq 8$の全てのxの値に対して、不等式$x^2-2mx+m+6 \gt 0$が
成り立つような定数mの値の範囲を求めよ。
福田の一夜漬け数学〜２次関数・２次不等式(1)〜高校1年生
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x^2-7x-60 \gt 0$
$2x^2+5x-3 \lt 0$
$2x^2-3x-1 \geqq 0$
$-x^2+2x+1 \geqq 0$
$x^2-8x+16 \leqq 0$
$-4x^2+4x-1 \lt 0$
$x^2-4x+5 \gt 0$
$-2x^2+4x-5 \gt 0$
を満たすようなxの範囲をそれぞれ求めよ。
この動画を見る
$x^2-7x-60 \gt 0$
$2x^2+5x-3 \lt 0$
$2x^2-3x-1 \geqq 0$
$-x^2+2x+1 \geqq 0$
$x^2-8x+16 \leqq 0$
$-4x^2+4x-1 \lt 0$
$x^2-4x+5 \gt 0$
$-2x^2+4x-5 \gt 0$
を満たすようなxの範囲をそれぞれ求めよ。
福田の一夜漬け数学〜２次関数の最大最小(4)置き換えと遺言〜高校1年生
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$y=x^4-2x^2-3$ の最小値とそのときの$x$を求めよ。
$y=2(x^2+2x)^2$$-4(x^2+2x)$$+3$ の最小値とそのときの$x$を求めよ。
$x \geqq 0,y \geqq 0,x+y=1$のとき、$xy$の最小値とそのときの$x,y$の値を求めよ。
問 $P=x^2-2xy+3y^2$$-2x+10y$$+2$の最小値を求めよ。
この動画を見る
$y=x^4-2x^2-3$ の最小値とそのときの$x$を求めよ。
$y=2(x^2+2x)^2$$-4(x^2+2x)$$+3$ の最小値とそのときの$x$を求めよ。
$x \geqq 0,y \geqq 0,x+y=1$のとき、$xy$の最小値とそのときの$x,y$の値を求めよ。
問 $P=x^2-2xy+3y^2$$-2x+10y$$+2$の最小値を求めよ。
福田の一夜漬け数学〜２次関数の最大最小(3)区間の動く最大最小〜高校1年生
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
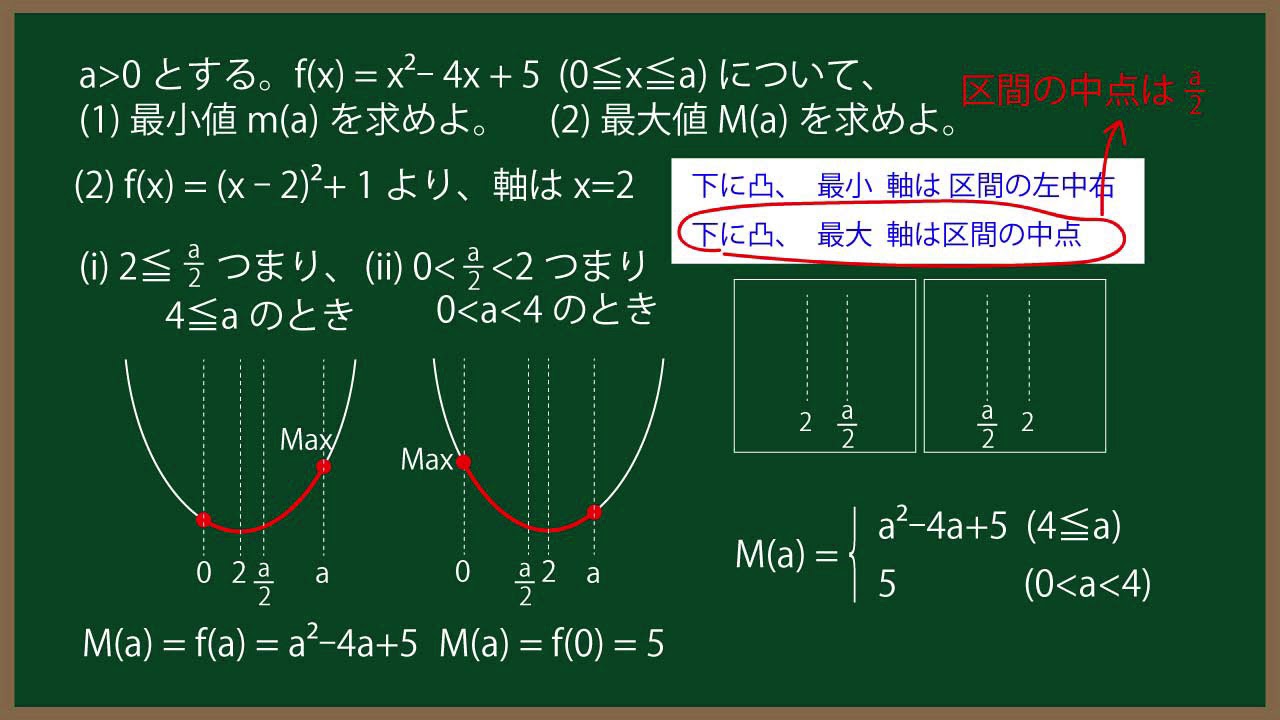
$a \gt 0$とする。$f(x)=x^2-4x+5$ $(0 \leqq x \leqq a)$について、
(1)最小値$m(a)$を求めよ。 (2)最大値$M(a)$を求めよ。
$f(x)=-x^2+4x-1$ $(a \leqq x \leqq a+1)$について
(1)最大値$M(a)$を求めよ。 (2)最小値$m(a)$を求めよ。
この動画を見る
$a \gt 0$とする。$f(x)=x^2-4x+5$ $(0 \leqq x \leqq a)$について、
(1)最小値$m(a)$を求めよ。 (2)最大値$M(a)$を求めよ。
$f(x)=-x^2+4x-1$ $(a \leqq x \leqq a+1)$について
(1)最大値$M(a)$を求めよ。 (2)最小値$m(a)$を求めよ。
福田の一夜漬け数学〜２次関数の最大最小(2)軸の動く最大最小〜高校1年生
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
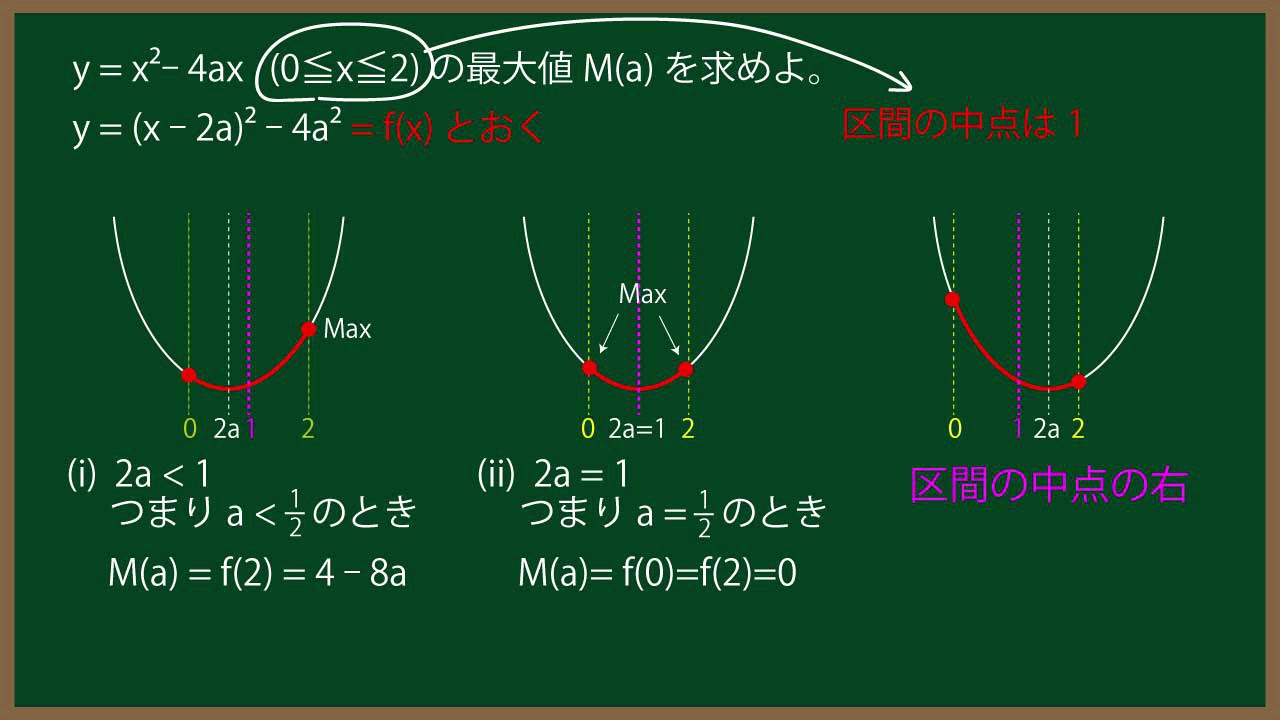
$y=x^2-4ax (0 \leqq x \leqq 2)$の最小値$m(a)$を求めよ。
$y=x^2-4ax (0 \leqq x \leqq 2)$の最大値$M(a)$を求めよ。
$y=M(a),y=m(a)$のグラフを描け。
$M(a)=\begin{eqnarray}
\left\{
\begin{array}{l}
4-8a (a \lt \frac{1}{2}) \\
0 (a \geqq \frac{1}{2})
\end{array}
\right.
\end{eqnarray}$
$m(a)=\begin{eqnarray}
\left\{
\begin{array}{l}
0 (a \lt 0) \\
-4a^2 (0 \leqq a \leqq 1) \\
4-8a (1 \lt a)
\end{array}
\right.
\end{eqnarray}$
$y=-x^2-ax+a (0 \leqq x \leqq 1)$の最小値$m(a)$を求めよ。
この動画を見る
$y=x^2-4ax (0 \leqq x \leqq 2)$の最小値$m(a)$を求めよ。
$y=x^2-4ax (0 \leqq x \leqq 2)$の最大値$M(a)$を求めよ。
$y=M(a),y=m(a)$のグラフを描け。
$M(a)=\begin{eqnarray}
\left\{
\begin{array}{l}
4-8a (a \lt \frac{1}{2}) \\
0 (a \geqq \frac{1}{2})
\end{array}
\right.
\end{eqnarray}$
$m(a)=\begin{eqnarray}
\left\{
\begin{array}{l}
0 (a \lt 0) \\
-4a^2 (0 \leqq a \leqq 1) \\
4-8a (1 \lt a)
\end{array}
\right.
\end{eqnarray}$
$y=-x^2-ax+a (0 \leqq x \leqq 1)$の最小値$m(a)$を求めよ。
福田の一夜漬け数学〜２次関数の最大最小(1)〜高校1年生
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
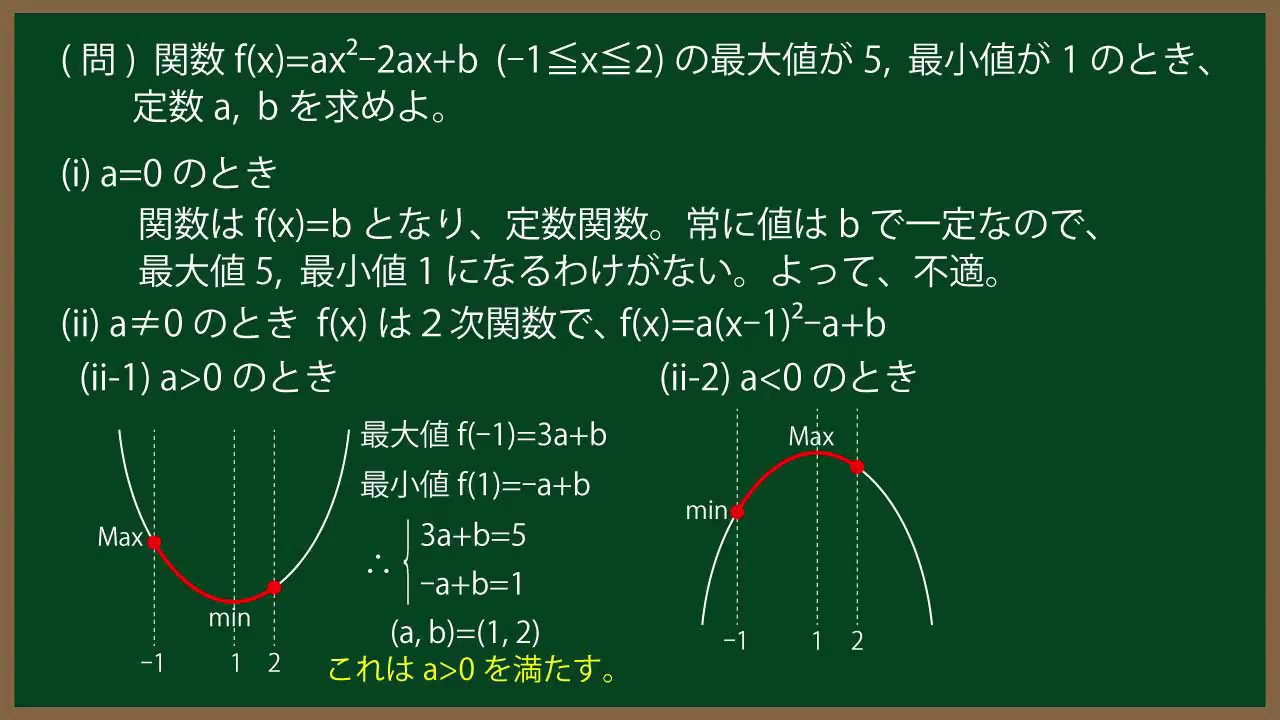
(問)関数$f(x)=ax^2-2ax+b$ $(-1 \leqq x \leqq 2)$の最大値が5,最小値は$1$のとき、
定数$a,b$を求めよ。
この動画を見る
(問)関数$f(x)=ax^2-2ax+b$ $(-1 \leqq x \leqq 2)$の最大値が5,最小値は$1$のとき、
定数$a,b$を求めよ。
【受験対策】数学－関数１２
単元：
#数Ⅰ#数Ⅱ#２次関数#2次関数とグラフ#三角関数#三角関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①右の図1は, $y = 2x,y = 3x,y =-2x,y =-3x$の
グラフをそれぞれ表している.
このとき,$y =-2x$のグラフを
ア~エから1つ選び,その記号を書きなさい.
右の図2で,直線$\ell$は関数$y =\dfrac{1}{2}x - 3$ のグラフ,
直線$m$は$y = \dfrac{1}{2}x + 5$ のグラフで,
2点,$A,B$は直線$\ell$上の点,2点$C,D$は直線$m$上の点で,
四角形$ABDC$は平行四辺形である.
点$A$の$x$座標が$-2$,点$B$の$y$座標が$-1$のとき,
次の②,③に答えなさい.
②点$C$の$x$座標が$3$のとき,点$D$の座標を求めなさい.
③ 四角形$ABDC$の面積を求めなさい.
図は動画内参照
この動画を見る
①右の図1は, $y = 2x,y = 3x,y =-2x,y =-3x$の
グラフをそれぞれ表している.
このとき,$y =-2x$のグラフを
ア~エから1つ選び,その記号を書きなさい.
右の図2で,直線$\ell$は関数$y =\dfrac{1}{2}x - 3$ のグラフ,
直線$m$は$y = \dfrac{1}{2}x + 5$ のグラフで,
2点,$A,B$は直線$\ell$上の点,2点$C,D$は直線$m$上の点で,
四角形$ABDC$は平行四辺形である.
点$A$の$x$座標が$-2$,点$B$の$y$座標が$-1$のとき,
次の②,③に答えなさい.
②点$C$の$x$座標が$3$のとき,点$D$の座標を求めなさい.
③ 四角形$ABDC$の面積を求めなさい.
図は動画内参照
【受験対策】数学－関数１１
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①関数$y=-\dfrac{32}{x}$について,
$x$の変域が$-8\leqq x \leqq -2$のとき,$y$の変域を求めよう.
②関数$y=-\dfrac{1}{2}x^2$について,
$x$の変域が$-4 \leqq x\leqq 2$のとき,$y$の変域を求めよう.
③右の図で,点$A(12,18)$,点$B(0,9)$で,点$C$は線分$OA$上の点で,
点$D$は$BC$の延長と$x$軸との交点である.
曲線$\ell$は関数$y=\dfrac{a}{x}(a \gt 0)$の面積と
$\triangle OCD$の面積が等しいとき,
$a$の値を求めよう.
図は動画内参照
この動画を見る
①関数$y=-\dfrac{32}{x}$について,
$x$の変域が$-8\leqq x \leqq -2$のとき,$y$の変域を求めよう.
②関数$y=-\dfrac{1}{2}x^2$について,
$x$の変域が$-4 \leqq x\leqq 2$のとき,$y$の変域を求めよう.
③右の図で,点$A(12,18)$,点$B(0,9)$で,点$C$は線分$OA$上の点で,
点$D$は$BC$の延長と$x$軸との交点である.
曲線$\ell$は関数$y=\dfrac{a}{x}(a \gt 0)$の面積と
$\triangle OCD$の面積が等しいとき,
$a$の値を求めよう.
図は動画内参照
【高校数学】 数Ⅰ－７３ 特殊な最大・最小③
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎x,yが$x^2+y^2=16$を満たすとき、$6x+y^2$の最大値と最小値を求めよう。
この動画を見る
◎x,yが$x^2+y^2=16$を満たすとき、$6x+y^2$の最大値と最小値を求めよう。
【高校数学】 数Ⅰ－７２ ２次関数と共有点⑤
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎2次方程式$2x^2-5x+a=0$の1つの解が0と1の間にあり、ほかの解が2と3の間にあるように、定数aの値の範囲を定めよう。
この動画を見る
◎2次方程式$2x^2-5x+a=0$の1つの解が0と1の間にあり、ほかの解が2と3の間にあるように、定数aの値の範囲を定めよう。
【高校数学】 数Ⅰ－７１ ２次関数と共有点④
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎2次関数$y=x^2-ax-a+3$のグラフが次のようになるとき、定数aの値の範囲は？
①x軸の正の部分と、異なる2点で交わる。
②x軸と、制の部分と負の部分で交わる。
③x軸の$x \lt -2$の部分と、異なる2点で交わる。
この動画を見る
◎2次関数$y=x^2-ax-a+3$のグラフが次のようになるとき、定数aの値の範囲は？
①x軸の正の部分と、異なる2点で交わる。
②x軸と、制の部分と負の部分で交わる。
③x軸の$x \lt -2$の部分と、異なる2点で交わる。
【高校数学】 数Ⅰ－５３ 特殊な最大・最小②
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎x.yを変数とするとき、$x^2-4xy+7y^2-4y+3$の最小値とそのときのx、yの値を求めよう。
この動画を見る
◎x.yを変数とするとき、$x^2-4xy+7y^2-4y+3$の最小値とそのときのx、yの値を求めよう。
【高校数学】 数Ⅰ－５２ 特殊な最大・最小①
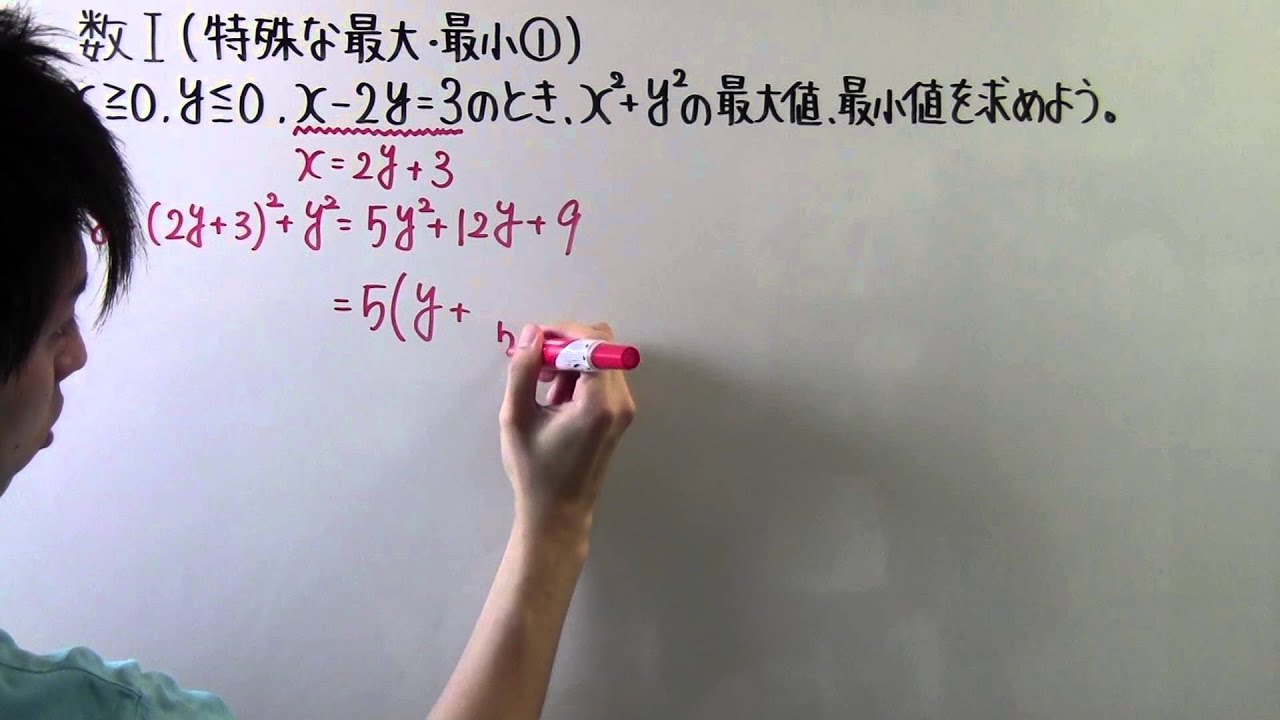
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎$x \geqq 0 , y \leqq 0,x-2y=3$のとき、$x^2+y^2$の最大値、最小値を求めよう。
この動画を見る
◎$x \geqq 0 , y \leqq 0,x-2y=3$のとき、$x^2+y^2$の最大値、最小値を求めよう。
【高校数学】 数Ⅰ－５１ ２次関数の決定③
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎次の条件を満たす放物線の方程式を求めよう。
①放物線$y=2x^2-3x$を平行移動した曲線で、2点(1.-1)(2.0)を通る。
②放物線$y=x^2-3x+4$を平行移動した曲線で、点(2.4)を通り、頂点が 直線$y=2x+1$上にある。
この動画を見る
◎次の条件を満たす放物線の方程式を求めよう。
①放物線$y=2x^2-3x$を平行移動した曲線で、2点(1.-1)(2.0)を通る。
②放物線$y=x^2-3x+4$を平行移動した曲線で、点(2.4)を通り、頂点が 直線$y=2x+1$上にある。
【高校数学】 数Ⅰ－５０ ２次関数の決定②
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎2次関数のグラフが次の3点を通るとき、その2次関数を求めよう。
①(-1.-2)(3.18)(-2.3)
②(3.0)(1.4)(-1.0)
この動画を見る
◎2次関数のグラフが次の3点を通るとき、その2次関数を求めよう。
①(-1.-2)(3.18)(-2.3)
②(3.0)(1.4)(-1.0)
【高校数学】 数Ⅰ－４９ ２次関数の決定①
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎次の条件を満たす2次関数を求めよう。
①頂点が(1.-2)で、点(2、-3)を通る。
②グラフの軸がx=-1で、2点(-2.9)(1.3)を通る。
③X=2で最小値-4をとり、X=4のときy=8である。
この動画を見る
◎次の条件を満たす2次関数を求めよう。
①頂点が(1.-2)で、点(2、-3)を通る。
②グラフの軸がx=-1で、2点(-2.9)(1.3)を通る。
③X=2で最小値-4をとり、X=4のときy=8である。
【高校数学】 数Ⅰ－４８ ２次関数の最大・最小⑦
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$2x+y=1$のとき、$x^2+y^2$の最小値を求めよう。
②$x+2y=0$のとき、$xy$の最大値を求めよう。
この動画を見る
①$2x+y=1$のとき、$x^2+y^2$の最小値を求めよう。
②$x+2y=0$のとき、$xy$の最大値を求めよう。
【高校数学】 数Ⅰ－４７ ２次関数の最大・最小⑥ ・ 動く定義域編②
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎aは定数とする。関数$y=x^2-4x+5(a \leqq x \leqq a+1)$について。
①最小値を求めよう。
②最大値を求めよう。
この動画を見る
◎aは定数とする。関数$y=x^2-4x+5(a \leqq x \leqq a+1)$について。
①最小値を求めよう。
②最大値を求めよう。
【高校数学】 数Ⅰ－４６ ２次関数の最大・最小⑤ ・ 動く定義域編①
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎$a \gt 0$とする。関数$y=x^2-2x-1(0 \leqq x \leqq a)$について。
①最小値を求めよう。
②最大値を求めよう。
この動画を見る
◎$a \gt 0$とする。関数$y=x^2-2x-1(0 \leqq x \leqq a)$について。
①最小値を求めよう。
②最大値を求めよう。
【高校数学】 数Ⅰ－４５ ２次関数の最大・最小④ ・ 動く軸編
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
aは定数とする。関数$y=x^2-2ax+a(0 \leqq x \leqq 2)$の最大値、最小値を、次の各場合について求めよう。
①$a \leqq 0$
②$0 \lt a \lt 1$
③$a=1$
④$1 \lt a \lt 2$
⑤$a \geqq 2$
この動画を見る
aは定数とする。関数$y=x^2-2ax+a(0 \leqq x \leqq 2)$の最大値、最小値を、次の各場合について求めよう。
①$a \leqq 0$
②$0 \lt a \lt 1$
③$a=1$
④$1 \lt a \lt 2$
⑤$a \geqq 2$
【高校数学】数Ⅰ-44 ２次関数の最大・最小③
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$y=3x^2+6x+C(-2 \leqq x \leqq 1)$の最大値が7となるような、定数Cの値を求めよう。
◎xの2次関数$y=x^2+2mx+3m$の最小値をkとする。
②kをmの式で表そう。
③kの値を最大にするmの値と、kの値を求めよう。
この動画を見る
①$y=3x^2+6x+C(-2 \leqq x \leqq 1)$の最大値が7となるような、定数Cの値を求めよう。
◎xの2次関数$y=x^2+2mx+3m$の最小値をkとする。
②kをmの式で表そう。
③kの値を最大にするmの値と、kの値を求めよう。
【高校数学】数Ⅰ-43 ２次関数の最大・最小②
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎次の2次関数に最大値、最小値があれば、それを求めよう。
①$y=2x^2-3(-2 \leqq x \leqq 3)$
②$y=-3x^2+6x+2(-1 \leqq x \leqq 3)$
③$y=x^2-4x+2(-2 \lt x \leqq 4)$
④$y=\displaystyle \frac{1}{3}x^2+2x+2(-2 \leqq x \lt 1)$
この動画を見る
◎次の2次関数に最大値、最小値があれば、それを求めよう。
①$y=2x^2-3(-2 \leqq x \leqq 3)$
②$y=-3x^2+6x+2(-1 \leqq x \leqq 3)$
③$y=x^2-4x+2(-2 \lt x \leqq 4)$
④$y=\displaystyle \frac{1}{3}x^2+2x+2(-2 \leqq x \lt 1)$
【高校数学】数Ⅰ-42 ２次関数の最大・最小 ①
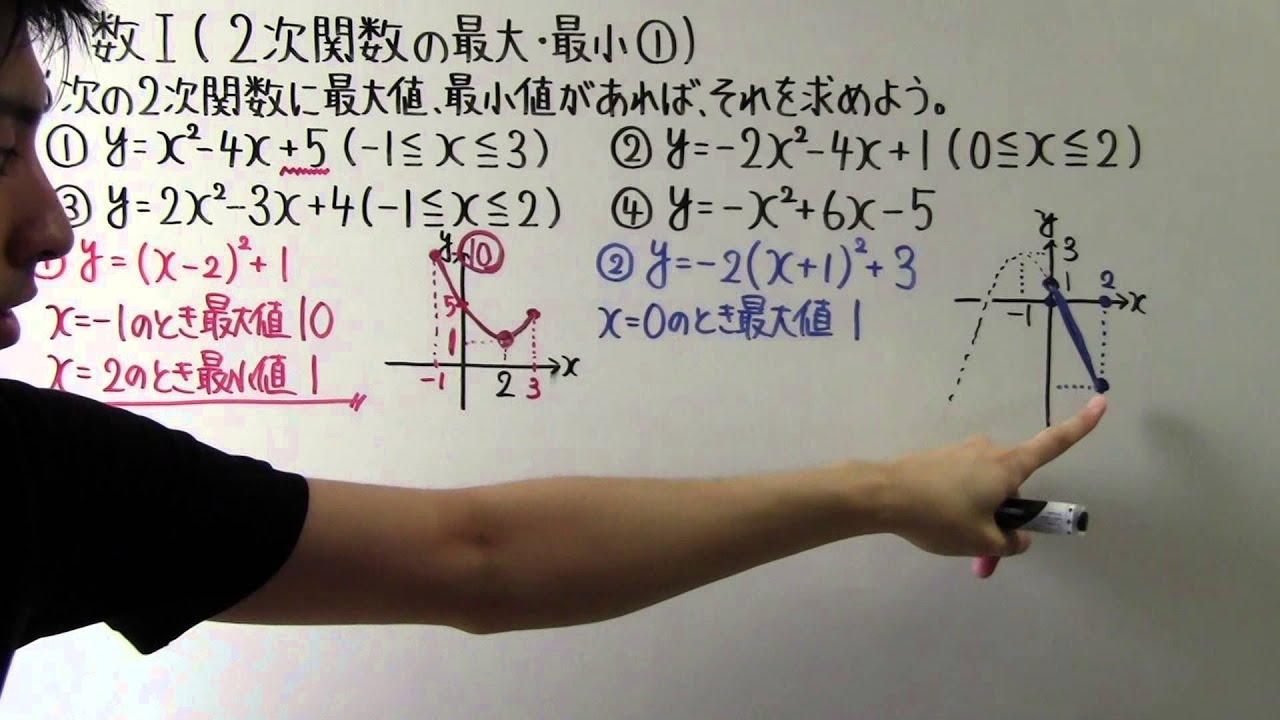
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎次の2次関数に最大値、最小値があれば、それを求めよう。
①$y=x^2-4x+5(-1 \leqq x \leqq 3)$
②$y=-2x^2-4x+1(0 \leqq x \leqq 2)$
③$y=2x^2-3x+4(-1 \leqq x \leqq 2)$
④$y=x^2+6x-5$
この動画を見る
◎次の2次関数に最大値、最小値があれば、それを求めよう。
①$y=x^2-4x+5(-1 \leqq x \leqq 3)$
②$y=-2x^2-4x+1(0 \leqq x \leqq 2)$
③$y=2x^2-3x+4(-1 \leqq x \leqq 2)$
④$y=x^2+6x-5$
【高校数学】数Ⅰ-41 ２次関数⑦(移動編)
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①放物線$y=-2x^2-4x+1$をx軸方向に3、y軸方向に-1だけ平行移動して得られる放物線の方程式を求めよう。
②放物線$y=-2x^2-4x+3$の、x軸、y軸、原点それぞれに関する対称移動後の放物線の方程式を求めよう。
この動画を見る
①放物線$y=-2x^2-4x+1$をx軸方向に3、y軸方向に-1だけ平行移動して得られる放物線の方程式を求めよう。
②放物線$y=-2x^2-4x+3$の、x軸、y軸、原点それぞれに関する対称移動後の放物線の方程式を求めよう。
【高校数学】数Ⅰ-40 ２次関数⑥
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎2次関数$y=ax^2+bx+c$のグラフが右の図のようになる時、次の値の符号を調べよう。
①$a$
②$b$
③$c$
④$b^2-ac$
⑤$a-b+c$
⑥$a+b+c$
※図は動画内参照
この動画を見る
◎2次関数$y=ax^2+bx+c$のグラフが右の図のようになる時、次の値の符号を調べよう。
①$a$
②$b$
③$c$
④$b^2-ac$
⑤$a-b+c$
⑥$a+b+c$
※図は動画内参照
【高校数学】数Ⅰ-39 ２次関数⑤(平方完成の練習編)
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎次の2次式を平方完成しよう。
①$y=x^2+2x-1$
②$y=2x^2-8x-6$
③$y=x^2-4x$
④$y=-2x^26x+3$
⑤$y=3x^2-5x+2$
⑥$y=\displaystyle \frac{1}{3}x^2+4x$
この動画を見る
◎次の2次式を平方完成しよう。
①$y=x^2+2x-1$
②$y=2x^2-8x-6$
③$y=x^2-4x$
④$y=-2x^26x+3$
⑤$y=3x^2-5x+2$
⑥$y=\displaystyle \frac{1}{3}x^2+4x$
【高校数学】数Ⅰ-38 ２次関数④(平方完成編)
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$y=ax^2+bx+c$を平方完成すると①y=①＿＿＿＿＿＿＿＿＿＿＿＿となり、軸は②x=＿＿＿＿＿＿＿＿、頂点は③(＿＿＿＿,＿＿＿＿)となる。
◎次の2次式を平方完成しよう。
④$y=x^2-4x+6$
⑤$y=2x^2+8x+3$
⑥$y=-3x^2-18x-17$
この動画を見る
$y=ax^2+bx+c$を平方完成すると①y=①＿＿＿＿＿＿＿＿＿＿＿＿となり、軸は②x=＿＿＿＿＿＿＿＿、頂点は③(＿＿＿＿,＿＿＿＿)となる。
◎次の2次式を平方完成しよう。
④$y=x^2-4x+6$
⑤$y=2x^2+8x+3$
⑥$y=-3x^2-18x-17$
【高校数学】数Ⅰ-37 ２次関数③(軸と頂点編)
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎次の2次関数の軸と頂点を求めよう。
①$y=3(x--1)^2-4$
②$y=2x^2+7$
この動画を見る
◎次の2次関数の軸と頂点を求めよう。
①$y=3(x--1)^2-4$
②$y=2x^2+7$
【高校数学】数Ⅰ-36 ２次関数②(値域編)
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎次の関数の値域を求めよう。また、最大値、最小値があれば、それをもとめよう。
①$y=2x+1(2 \leqq x \leqq 3)$
②$y=-3x+2(-1 \leqq x \leqq 2)$
③$y=x^2(-3 \leqq x \leqq 1)$
④$y=3x-5(1 \leqq x \lt 4)$
この動画を見る
◎次の関数の値域を求めよう。また、最大値、最小値があれば、それをもとめよう。
①$y=2x+1(2 \leqq x \leqq 3)$
②$y=-3x+2(-1 \leqq x \leqq 2)$
③$y=x^2(-3 \leqq x \leqq 1)$
④$y=3x-5(1 \leqq x \lt 4)$