２次関数
２次関数
学習院大 三次方程式と複素数 高校数学 Mathematics Japanese university entrance exam
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#複素数と方程式#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#学習院大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
'04学習院大学過去問題
a実数
$f(x)=4x^3-4ax^2+(a^2+3)x+a^2+4a+7$
(1)任意のaについてf(m)=0が成り立つ実数m
(2)f(x)=0の3つの解を複素数平面上に図示したとき、それらが正三角形になるようなaの値
この動画を見る
'04学習院大学過去問題
a実数
$f(x)=4x^3-4ax^2+(a^2+3)x+a^2+4a+7$
(1)任意のaについてf(m)=0が成り立つ実数m
(2)f(x)=0の3つの解を複素数平面上に図示したとき、それらが正三角形になるようなaの値
東京理科大 指数方程式 実数解の条件 Mathematics Japanese university entrance exam
単元：
#数Ⅱ#大学入試過去問(数学)#２次関数#式と証明#2次方程式と2次不等式#指数関数と対数関数#恒等式・等式・不等式の証明#指数関数#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
'07東京理科大学過去問題
$9^x+9^{-x}-(a+1)(3^x+3^{-x})-2a^2+8a-4$
$=0$
(1)$a=-5$のとき、解け
(2)実数解をもつaの範囲
この動画を見る
'07東京理科大学過去問題
$9^x+9^{-x}-(a+1)(3^x+3^{-x})-2a^2+8a-4$
$=0$
(1)$a=-5$のとき、解け
(2)実数解をもつaの範囲
横浜市（医）複素数の２次方程式 高校数学 Mathematics Japanese university entrance exam
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#複素数と方程式#2次方程式と2次不等式#複素数#学校別大学入試過去問解説(数学)#数学(高校生)#横浜市立大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
'00横浜市立大学過去問題
虚部が正の複素数Zで$iZ^2+2iZ+\frac{1}{2}+i=0$をみたすZを
$Z=a+bi$(a,b実数.b＞0)の形で求めよ。
この動画を見る
'00横浜市立大学過去問題
虚部が正の複素数Zで$iZ^2+2iZ+\frac{1}{2}+i=0$をみたすZを
$Z=a+bi$(a,b実数.b＞0)の形で求めよ。
【高校数学】２次不等式②～連立不等式・基礎と応用～ 2-12【数学Ⅰ】
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
$(1)次の連立不等式を解け$
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2+x-2\lt 0 \\
x^2+x\geqq b
\end{array}
\right.
\end{eqnarray}$
$(2)2次関数y=x^2-2mx-m+2\\$
$とx軸の正の部分が異なる2点で交わるように$
$定数mの範囲を求めよ$
この動画を見る
$(1)次の連立不等式を解け$
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2+x-2\lt 0 \\
x^2+x\geqq b
\end{array}
\right.
\end{eqnarray}$
$(2)2次関数y=x^2-2mx-m+2\\$
$とx軸の正の部分が異なる2点で交わるように$
$定数mの範囲を求めよ$
慶應義塾 二次式 高校数学 Mathematics Japanese university entrance exa
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#式と証明#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
慶応義塾大学過去問題
a,b,cは実数
$v(y)=acy^2+(ab+bc)y+a^2+b^2+c^2-2ac$
$-2 \leqq y \leqq 2$の範囲で$v(y) \geqq 0$であることを示せ
この動画を見る
慶応義塾大学過去問題
a,b,cは実数
$v(y)=acy^2+(ab+bc)y+a^2+b^2+c^2-2ac$
$-2 \leqq y \leqq 2$の範囲で$v(y) \geqq 0$であることを示せ
【高校数学】２次不等式①～これで理解できるくね？～ 2-11【数学Ⅰ】
【高校数学】2次方程式④～放物線と直線の共有点～ 2-10【数学Ⅰ】
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
(1)放物線y=x²-4x+5と直線y=x+1の共有点の座標を求めよ。
(2)放物線y=x²-1と直線y=2x-kが接するとき、定数kの値を求めよ。
この動画を見る
(1)放物線y=x²-4x+5と直線y=x+1の共有点の座標を求めよ。
(2)放物線y=x²-1と直線y=2x-kが接するとき、定数kの値を求めよ。
【高校数学】２次方程式3 5 ～例題で学ぶ判別式D～ 2-9.5【数学Ⅰ】
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
(1)2次方程式x²-6x+m=0が異なる2つの実数解をもつように、定数mの値の範囲を求めよ。
(2)2次方程式x²-mx+2=0が重解をもつように、定数mの値を定めよ。
(3)2次関数y=-x²+2x+mのグラフとx軸の共有点の個数は、定数mの値によってどのように
変わるか。
この動画を見る
(1)2次方程式x²-6x+m=0が異なる2つの実数解をもつように、定数mの値の範囲を求めよ。
(2)2次方程式x²-mx+2=0が重解をもつように、定数mの値を定めよ。
(3)2次関数y=-x²+2x+mのグラフとx軸の共有点の個数は、定数mの値によってどのように
変わるか。
【高校数学】２次方程式③～グラフと２次方程式～ 2-9【数学Ⅰ】
【高校数学】２次方程式①～新たな解の公式～ 2-7【数学Ⅰ】
福田の一夜漬け数学〜図形と方程式〜軌跡(1)軌跡の鉄則、高校2年生
単元：
#数Ⅰ#数Ⅱ#２次関数#2次関数とグラフ#図形と方程式#軌跡と領域#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$ 放物線$y=x^2-2(a+1)x+2a$ $\cdots$①の頂点を$P$とする。$a$が$1$より大きい
実数を動くとき、点Pの軌跡を求めよ。
この動画を見る
${\Large\boxed{1}}$ 放物線$y=x^2-2(a+1)x+2a$ $\cdots$①の頂点を$P$とする。$a$が$1$より大きい
実数を動くとき、点Pの軌跡を求めよ。
放物線 光は1点に集る
単元：
#数Ⅰ#数Ⅱ#２次関数#三角関数#微分法と積分法#加法定理とその応用#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$y=x$に$y$軸ｔ平行に入った光はある一点を必ず通ることを示せ.
この動画を見る
$y=x$に$y$軸ｔ平行に入った光はある一点を必ず通ることを示せ.
福田の一夜漬け数学〜図形と方程式〜直線の方程式(4)直線群と２次方程式の解、高校2年生
単元：
#数Ⅰ#数Ⅱ#２次関数#2次方程式と2次不等式#2次関数とグラフ#図形と方程式#点と直線#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
{\Large\boxed{1}} 2直線4x+3y+2=0 \cdots①, 5x-2y-3=0 \cdots②の交点を通り、\\
点A(-1,2)を通る直線の方程式を求めよ。\\
\\
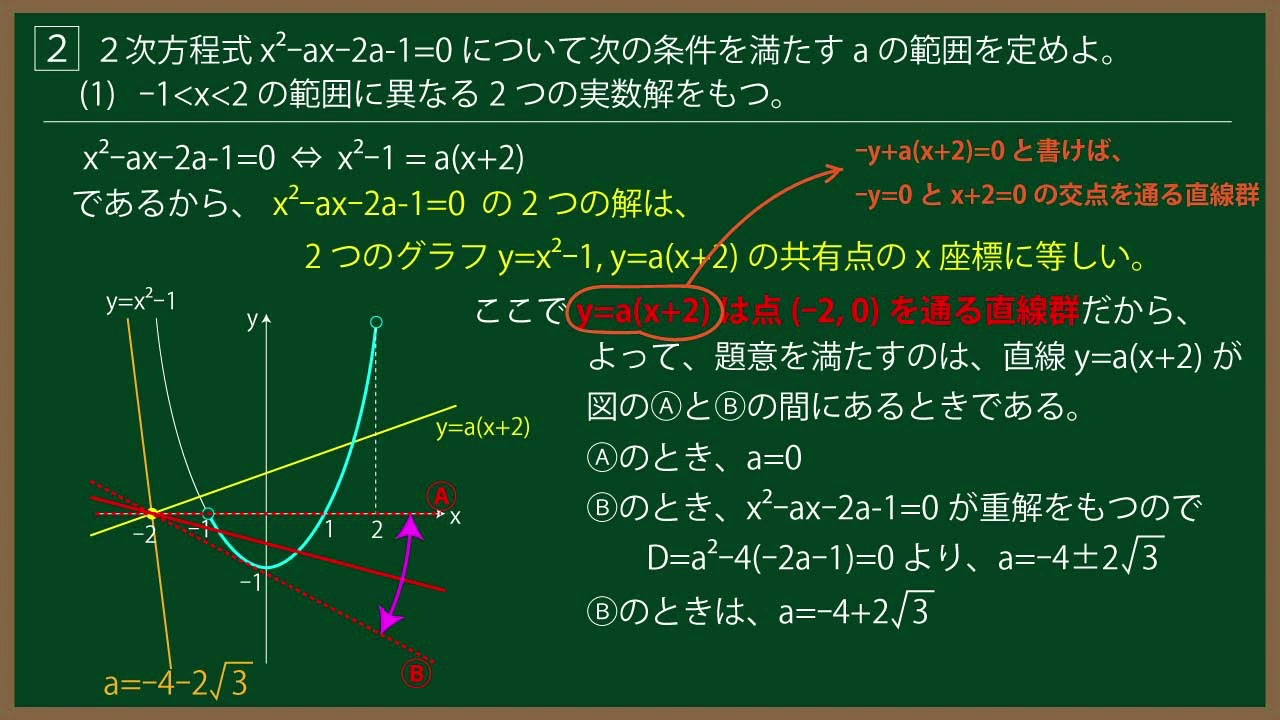
{\Large\boxed{2}} 2次方程式x^2-ax-2a-1=0 について次の条件を満たすaの範囲を定めよ。\\
(1)-1 \lt x \lt 2 の範囲に異なる2つの実数解をもつ。\\
(2)少なくとも1つ-1 \lt x \lt 2 の範囲に実数解をもつ。
\end{eqnarray}
この動画を見る
\begin{eqnarray}
{\Large\boxed{1}} 2直線4x+3y+2=0 \cdots①, 5x-2y-3=0 \cdots②の交点を通り、\\
点A(-1,2)を通る直線の方程式を求めよ。\\
\\
{\Large\boxed{2}} 2次方程式x^2-ax-2a-1=0 について次の条件を満たすaの範囲を定めよ。\\
(1)-1 \lt x \lt 2 の範囲に異なる2つの実数解をもつ。\\
(2)少なくとも1つ-1 \lt x \lt 2 の範囲に実数解をもつ。
\end{eqnarray}
群馬大/岐阜大 二次関数/二次方程式 高校数学 Japanese university entrance exam questions
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#2次関数とグラフ#岐阜大学#数学(高校生)#群馬大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
群馬大学過去問題
$y=x^2+ax+2$とA(0,1),B(2,3)を結ぶ線分ABと異なる2点で交わるaの範囲。
岐阜大学過去問題
$mx^2+5(m+1)x+4(m+2)=0$が有理数の解をもつ整数mの値
この動画を見る
群馬大学過去問題
$y=x^2+ax+2$とA(0,1),B(2,3)を結ぶ線分ABと異なる2点で交わるaの範囲。
岐阜大学過去問題
$mx^2+5(m+1)x+4(m+2)=0$が有理数の解をもつ整数mの値
京大 信州大 整数 ２次方程式 高校数学 Japanese university entrance exam questions Kyoto University
単元：
#数Ⅰ#数A#大学入試過去問(数学)#２次関数#2次関数とグラフ#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#信州大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
京都大学過去問題
①$n$と$n^2+2$がともに素数となるような自然数$n$を求めよ。
信州大学過去問題
②$x^2+(2a-1)x+a^2-3a-4=0$が少なくとも1つの正の解をもつ条件。
この動画を見る
京都大学過去問題
①$n$と$n^2+2$がともに素数となるような自然数$n$を求めよ。
信州大学過去問題
②$x^2+(2a-1)x+a^2-3a-4=0$が少なくとも1つの正の解をもつ条件。
東大 微分 代講ヨビノリたくみ Japanese university entrance exam questions Tokyo University
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
'98東京大学過去問題
aは0でない実数
関数
$f(x)=(3x^2-4)(x-a+\frac{1}{a})$の極大値と極小値の差が最小となるaを求めよ。
この動画を見る
'98東京大学過去問題
aは0でない実数
関数
$f(x)=(3x^2-4)(x-a+\frac{1}{a})$の極大値と極小値の差が最小となるaを求めよ。
福田の一夜漬け数学〜２次関数・異なる実数解の個数〜高校1年生
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}} k$は定数。方程式$|x^2-x-2|=k$ の異なる実数解の
個数を調べよ。
${\Large\boxed{2}} k$は定数。方程式$|x^2-x-2|=2x+k$ の異なる実数解の
個数を調べよ。
この動画を見る
${\Large\boxed{1}} k$は定数。方程式$|x^2-x-2|=k$ の異なる実数解の
個数を調べよ。
${\Large\boxed{2}} k$は定数。方程式$|x^2-x-2|=2x+k$ の異なる実数解の
個数を調べよ。
福田の一夜漬け数学〜２次関数・解の存在範囲(3)少なくとも１つ〜高校1年生
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}} x^2+(2-m)x+4$$-2m$$=0$ が$-1 \lt x \lt 1$の範囲に少なくとも
1つ解をもつようなmの値の範囲を求めよ。
${\Large\boxed{2}} x^2+(2-m)x+4$$-2m$$=0$ が$-1 \leqq x \leqq 1$の範囲に少なくとも
1つ解をもつような$m$の値の範囲を求めよ。
(数学$\textrm{II}$の内容)
${\Large\boxed{3}}$ 実数$m$が$1 \leqq m \leqq 3$の範囲を動くとき
直線$y=2mx+m^2$ の通過する範囲を図示せよ。
この動画を見る
${\Large\boxed{1}} x^2+(2-m)x+4$$-2m$$=0$ が$-1 \lt x \lt 1$の範囲に少なくとも
1つ解をもつようなmの値の範囲を求めよ。
${\Large\boxed{2}} x^2+(2-m)x+4$$-2m$$=0$ が$-1 \leqq x \leqq 1$の範囲に少なくとも
1つ解をもつような$m$の値の範囲を求めよ。
(数学$\textrm{II}$の内容)
${\Large\boxed{3}}$ 実数$m$が$1 \leqq m \leqq 3$の範囲を動くとき
直線$y=2mx+m^2$ の通過する範囲を図示せよ。
福田の一夜漬け数学〜２次関数・解の存在範囲(2)〜高校1年生
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}} x^2+2mx-2m+3=0$ が次のような解をもつとき、定数
$m$の値の範囲を求めよ。
(1)2つの解がともに2より大
(2)2つの解がともに2と4の間
${\Large\boxed{2}} x^2+(m-1)x-$$m^2$$+2$$=0$ の1つの解が-2と0の間、
他の解が0と1の間にあるときのmの値の範囲は?
この動画を見る
${\Large\boxed{1}} x^2+2mx-2m+3=0$ が次のような解をもつとき、定数
$m$の値の範囲を求めよ。
(1)2つの解がともに2より大
(2)2つの解がともに2と4の間
${\Large\boxed{2}} x^2+(m-1)x-$$m^2$$+2$$=0$ の1つの解が-2と0の間、
他の解が0と1の間にあるときのmの値の範囲は?
福田の一夜漬け数学〜２次関数・解の存在範囲(1)〜高校1年生
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#2次関数とグラフ#解と判別式・解と係数の関係#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}} x^2-2mx-m+2=0$ が次のような解をもつとき、定数$m$の
値の範囲を求めよ。
(1)異なる2つの正の解
(2)異なる2つの負の解
(3)異符号の解
(4)2つの0以上の解
(5)2つの0以下の解
この動画を見る
${\Large\boxed{1}} x^2-2mx-m+2=0$ が次のような解をもつとき、定数$m$の
値の範囲を求めよ。
(1)異なる2つの正の解
(2)異なる2つの負の解
(3)異符号の解
(4)2つの0以上の解
(5)2つの0以下の解
福田の一夜漬け数学〜２次関数・２次不等式(2)絶対不等式〜高校1年生
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
① 任意の実数xに対して、不等式$ax^2-2\sqrt3x+a+2 \leqq 0$が成り立つ
ような定数aの範囲を求めよ。
②$0 \leqq x \leqq 8$の全てのxの値に対して、不等式$x^2-2mx+m+6 \gt 0$が
成り立つような定数mの値の範囲を求めよ。
この動画を見る
① 任意の実数xに対して、不等式$ax^2-2\sqrt3x+a+2 \leqq 0$が成り立つ
ような定数aの範囲を求めよ。
②$0 \leqq x \leqq 8$の全てのxの値に対して、不等式$x^2-2mx+m+6 \gt 0$が
成り立つような定数mの値の範囲を求めよ。
福田の一夜漬け数学〜２次関数・２次不等式(1)〜高校1年生
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x^2-7x-60 \gt 0$
$2x^2+5x-3 \lt 0$
$2x^2-3x-1 \geqq 0$
$-x^2+2x+1 \geqq 0$
$x^2-8x+16 \leqq 0$
$-4x^2+4x-1 \lt 0$
$x^2-4x+5 \gt 0$
$-2x^2+4x-5 \gt 0$
を満たすようなxの範囲をそれぞれ求めよ。
この動画を見る
$x^2-7x-60 \gt 0$
$2x^2+5x-3 \lt 0$
$2x^2-3x-1 \geqq 0$
$-x^2+2x+1 \geqq 0$
$x^2-8x+16 \leqq 0$
$-4x^2+4x-1 \lt 0$
$x^2-4x+5 \gt 0$
$-2x^2+4x-5 \gt 0$
を満たすようなxの範囲をそれぞれ求めよ。
福田の一夜漬け数学〜２次関数の最大最小(4)置き換えと遺言〜高校1年生
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$y=x^4-2x^2-3$ の最小値とそのときの$x$を求めよ。
$y=2(x^2+2x)^2$$-4(x^2+2x)$$+3$ の最小値とそのときの$x$を求めよ。
$x \geqq 0,y \geqq 0,x+y=1$のとき、$xy$の最小値とそのときの$x,y$の値を求めよ。
問 $P=x^2-2xy+3y^2$$-2x+10y$$+2$の最小値を求めよ。
この動画を見る
$y=x^4-2x^2-3$ の最小値とそのときの$x$を求めよ。
$y=2(x^2+2x)^2$$-4(x^2+2x)$$+3$ の最小値とそのときの$x$を求めよ。
$x \geqq 0,y \geqq 0,x+y=1$のとき、$xy$の最小値とそのときの$x,y$の値を求めよ。
問 $P=x^2-2xy+3y^2$$-2x+10y$$+2$の最小値を求めよ。
福田の一夜漬け数学〜２次関数の最大最小(3)区間の動く最大最小〜高校1年生
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
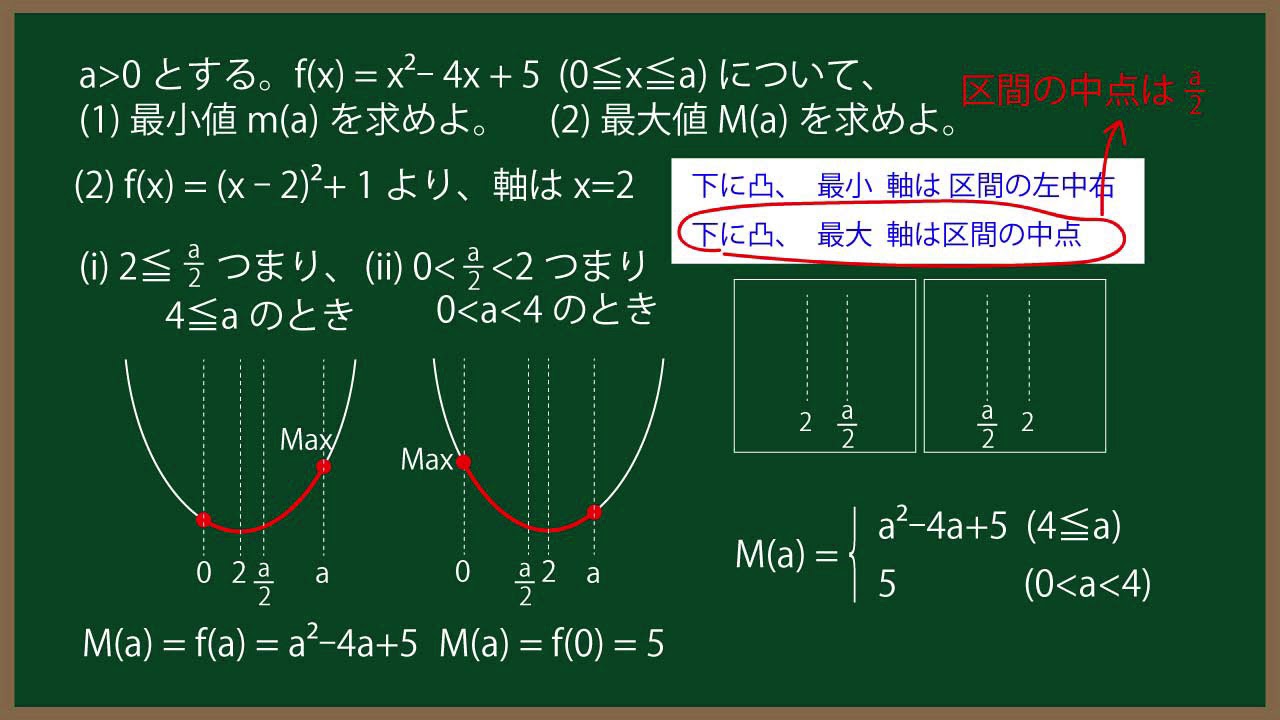
$a \gt 0$とする。$f(x)=x^2-4x+5$ $(0 \leqq x \leqq a)$について、
(1)最小値$m(a)$を求めよ。 (2)最大値$M(a)$を求めよ。
$f(x)=-x^2+4x-1$ $(a \leqq x \leqq a+1)$について
(1)最大値$M(a)$を求めよ。 (2)最小値$m(a)$を求めよ。
この動画を見る
$a \gt 0$とする。$f(x)=x^2-4x+5$ $(0 \leqq x \leqq a)$について、
(1)最小値$m(a)$を求めよ。 (2)最大値$M(a)$を求めよ。
$f(x)=-x^2+4x-1$ $(a \leqq x \leqq a+1)$について
(1)最大値$M(a)$を求めよ。 (2)最小値$m(a)$を求めよ。
福田の一夜漬け数学〜２次関数の最大最小(2)軸の動く最大最小〜高校1年生
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
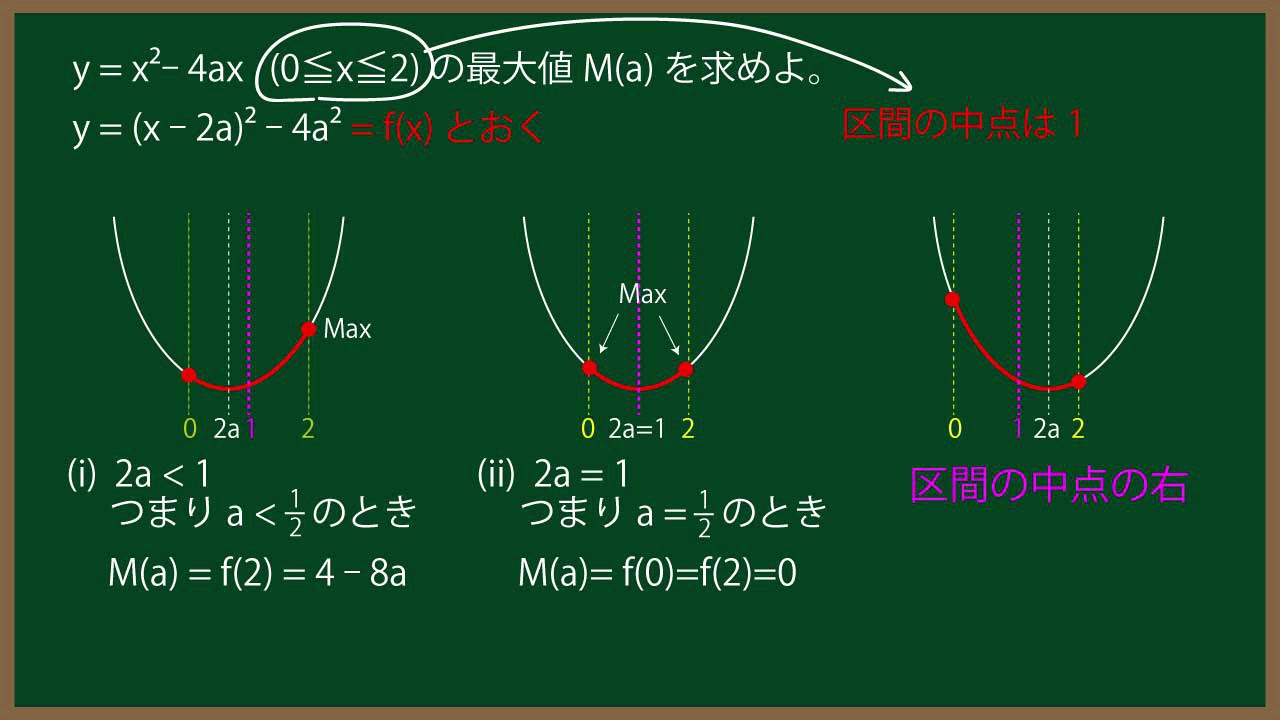
$y=x^2-4ax (0 \leqq x \leqq 2)$の最小値$m(a)$を求めよ。
$y=x^2-4ax (0 \leqq x \leqq 2)$の最大値$M(a)$を求めよ。
$y=M(a),y=m(a)$のグラフを描け。
$M(a)=\begin{eqnarray}
\left\{
\begin{array}{l}
4-8a (a \lt \frac{1}{2}) \\
0 (a \geqq \frac{1}{2})
\end{array}
\right.
\end{eqnarray}$
$m(a)=\begin{eqnarray}
\left\{
\begin{array}{l}
0 (a \lt 0) \\
-4a^2 (0 \leqq a \leqq 1) \\
4-8a (1 \lt a)
\end{array}
\right.
\end{eqnarray}$
$y=-x^2-ax+a (0 \leqq x \leqq 1)$の最小値$m(a)$を求めよ。
この動画を見る
$y=x^2-4ax (0 \leqq x \leqq 2)$の最小値$m(a)$を求めよ。
$y=x^2-4ax (0 \leqq x \leqq 2)$の最大値$M(a)$を求めよ。
$y=M(a),y=m(a)$のグラフを描け。
$M(a)=\begin{eqnarray}
\left\{
\begin{array}{l}
4-8a (a \lt \frac{1}{2}) \\
0 (a \geqq \frac{1}{2})
\end{array}
\right.
\end{eqnarray}$
$m(a)=\begin{eqnarray}
\left\{
\begin{array}{l}
0 (a \lt 0) \\
-4a^2 (0 \leqq a \leqq 1) \\
4-8a (1 \lt a)
\end{array}
\right.
\end{eqnarray}$
$y=-x^2-ax+a (0 \leqq x \leqq 1)$の最小値$m(a)$を求めよ。
福田の一夜漬け数学〜２次関数の最大最小(1)〜高校1年生
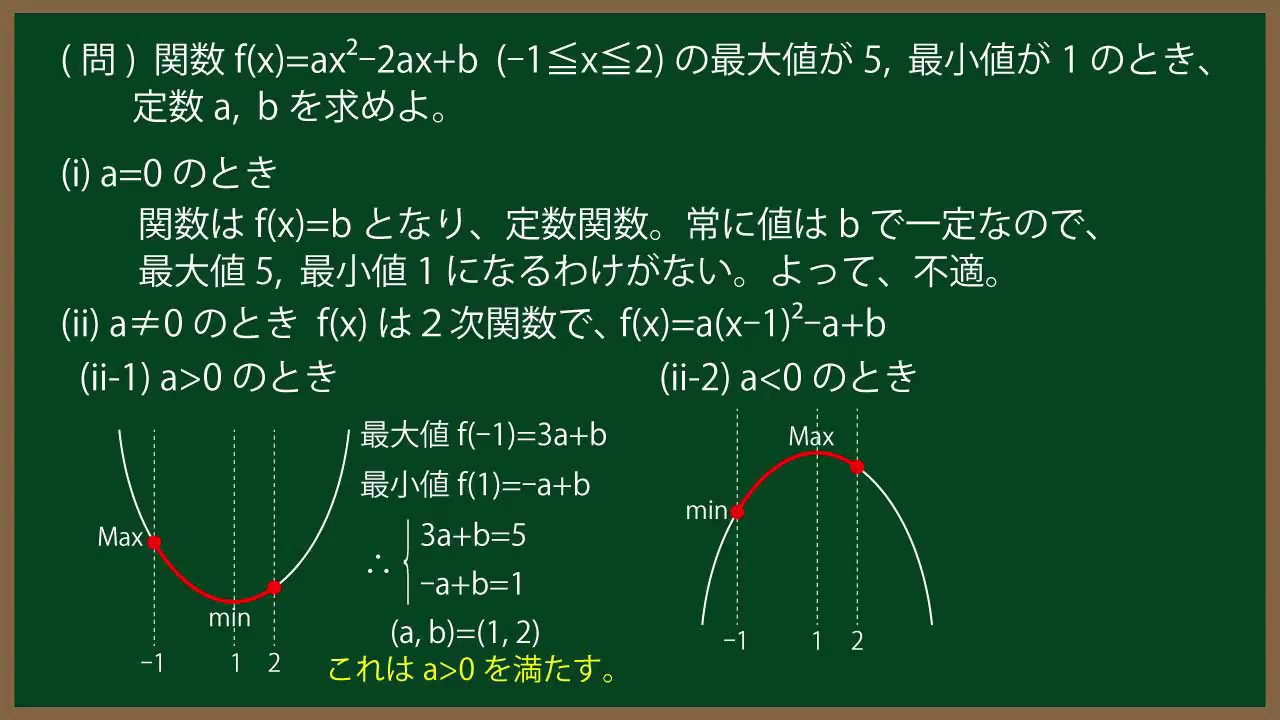
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
(問)関数$f(x)=ax^2-2ax+b$ $(-1 \leqq x \leqq 2)$の最大値が5,最小値は$1$のとき、
定数$a,b$を求めよ。
この動画を見る
(問)関数$f(x)=ax^2-2ax+b$ $(-1 \leqq x \leqq 2)$の最大値が5,最小値は$1$のとき、
定数$a,b$を求めよ。
放物線上の2点を通る直線の式を「3秒」で出だす方法
【受験対策】数学－関数１２
単元：
#数Ⅰ#数Ⅱ#２次関数#2次関数とグラフ#三角関数#三角関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①右の図1は, $y = 2x,y = 3x,y =-2x,y =-3x$の
グラフをそれぞれ表している.
このとき,$y =-2x$のグラフを
ア~エから1つ選び,その記号を書きなさい.
右の図2で,直線$\ell$は関数$y =\dfrac{1}{2}x - 3$ のグラフ,
直線$m$は$y = \dfrac{1}{2}x + 5$ のグラフで,
2点,$A,B$は直線$\ell$上の点,2点$C,D$は直線$m$上の点で,
四角形$ABDC$は平行四辺形である.
点$A$の$x$座標が$-2$,点$B$の$y$座標が$-1$のとき,
次の②,③に答えなさい.
②点$C$の$x$座標が$3$のとき,点$D$の座標を求めなさい.
③ 四角形$ABDC$の面積を求めなさい.
図は動画内参照
この動画を見る
①右の図1は, $y = 2x,y = 3x,y =-2x,y =-3x$の
グラフをそれぞれ表している.
このとき,$y =-2x$のグラフを
ア~エから1つ選び,その記号を書きなさい.
右の図2で,直線$\ell$は関数$y =\dfrac{1}{2}x - 3$ のグラフ,
直線$m$は$y = \dfrac{1}{2}x + 5$ のグラフで,
2点,$A,B$は直線$\ell$上の点,2点$C,D$は直線$m$上の点で,
四角形$ABDC$は平行四辺形である.
点$A$の$x$座標が$-2$,点$B$の$y$座標が$-1$のとき,
次の②,③に答えなさい.
②点$C$の$x$座標が$3$のとき,点$D$の座標を求めなさい.
③ 四角形$ABDC$の面積を求めなさい.
図は動画内参照
【受験対策】数学－関数１１
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①関数$y=-\dfrac{32}{x}$について,
$x$の変域が$-8\leqq x \leqq -2$のとき,$y$の変域を求めよう.
②関数$y=-\dfrac{1}{2}x^2$について,
$x$の変域が$-4 \leqq x\leqq 2$のとき,$y$の変域を求めよう.
③右の図で,点$A(12,18)$,点$B(0,9)$で,点$C$は線分$OA$上の点で,
点$D$は$BC$の延長と$x$軸との交点である.
曲線$\ell$は関数$y=\dfrac{a}{x}(a \gt 0)$の面積と
$\triangle OCD$の面積が等しいとき,
$a$の値を求めよう.
図は動画内参照
この動画を見る
①関数$y=-\dfrac{32}{x}$について,
$x$の変域が$-8\leqq x \leqq -2$のとき,$y$の変域を求めよう.
②関数$y=-\dfrac{1}{2}x^2$について,
$x$の変域が$-4 \leqq x\leqq 2$のとき,$y$の変域を求めよう.
③右の図で,点$A(12,18)$,点$B(0,9)$で,点$C$は線分$OA$上の点で,
点$D$は$BC$の延長と$x$軸との交点である.
曲線$\ell$は関数$y=\dfrac{a}{x}(a \gt 0)$の面積と
$\triangle OCD$の面積が等しいとき,
$a$の値を求めよう.
図は動画内参照
【高校数学】 数Ⅰ－７３ 特殊な最大・最小③
単元：
#数Ⅰ#２次関数#2次関数とグラフ#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎x,yが$x^2+y^2=16$を満たすとき、$6x+y^2$の最大値と最小値を求めよう。
この動画を見る
◎x,yが$x^2+y^2=16$を満たすとき、$6x+y^2$の最大値と最小値を求めよう。