三角形の辺の比（内分・外分・二等分線）
三角形の辺の比（内分・外分・二等分線）
15度75度90度の直角三角形の比は受験生は覚えた方が良い。また、導けますか？
福田の数学〜慶應義塾大学2023年医学部第３問〜接線が作る三角形
単元：
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#三角形の辺の比（内分・外分・二等分線）#図形と方程式#微分法と積分法#軌跡と領域#接線と増減表・最大値・最小値#関数と極限#微分とその応用#積分とその応用#数列の極限#微分法#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{3}$ 座標平面上の曲線y=$\frac{1}{x^2}$ (x $\ne$ 0)をCとする。$a_1$を正の実数とし、点$A_1$$\left(a_1, \frac{1}{a_1^2}\right)$におけるCの接線を$l_1$とする。$l_1$とCの交点で$A_1$と異なるものを$A_2$$\left(a_2, \frac{1}{a_2^2}\right)$とする。次に点$A_2$におけるCの接線を$l_2$とCの交点で$A_2$と異なるものを$A_3$$\left(a_3, \frac{1}{a_3^2}\right)$とする。以下、同様にしてn=3,4,5,...に対して、$A_n$$\left(a_n, \frac{1}{a_n^2}\right)$におけるCの接線を$l_n$とし、$l_n$とCの交点で$A_n$と異なるものを$A_{n+1}$$\left(a_{n+1}, \frac{1}{a_{n+1}^2}\right)$とする。
(1)$\frac{a_2}{a_1}$=$\boxed{\ \ あ\ \ }$であり、$\frac{a_3}{a_1}$=$\boxed{\ \ い\ \ }$である。
(2)$a_n$を$a_1$で表すと$a_n$=$\boxed{\ \ う\ \ }$である。無限級数$\displaystyle\sum_{n=1}^{\infty}a_n$の和をTを$a_1$を用いて表すとT=$\boxed{\ \ え\ \ }$である。
(3)$a_1$を正の実数すべてにわたって動かすとき、三角形$A_1A_2A_3$の重心が描く軌跡の方程式をy=f(x)の形で求めるとf(x)=$\boxed{\ \ お\ \ }$となる。
(4)三角形$A_1A_2A_3$が鋭角三角形になるための条件は$\boxed{\ \ か\ \ }$＜$a_1$＜$\boxed{\ \ き\ \ }$である。
(5)x軸上に2点$A'_1$($a_1$, 0), $A'_2$($a_2$, 0)をとり、台形$A_1A_2A'_2A'_1$の面積を$S_1$とする。また、点$A_1$から点$A_3$にいたる曲線Cの部分、および線分$A_3A_2$と$A_2A_1$で囲まれた図形の面積を$S_2$とする。このとき、$S_1$：$S_2$=$\boxed{\ \ く\ \ }$：$\boxed{\ \ け\ \ }$である。ただし、$\boxed{\ \ く\ \ }$と$\boxed{\ \ け\ \ }$は互いに素な自然数である。
2023慶應義塾大学医学部過去問
この動画を見る
$\Large\boxed{3}$ 座標平面上の曲線y=$\frac{1}{x^2}$ (x $\ne$ 0)をCとする。$a_1$を正の実数とし、点$A_1$$\left(a_1, \frac{1}{a_1^2}\right)$におけるCの接線を$l_1$とする。$l_1$とCの交点で$A_1$と異なるものを$A_2$$\left(a_2, \frac{1}{a_2^2}\right)$とする。次に点$A_2$におけるCの接線を$l_2$とCの交点で$A_2$と異なるものを$A_3$$\left(a_3, \frac{1}{a_3^2}\right)$とする。以下、同様にしてn=3,4,5,...に対して、$A_n$$\left(a_n, \frac{1}{a_n^2}\right)$におけるCの接線を$l_n$とし、$l_n$とCの交点で$A_n$と異なるものを$A_{n+1}$$\left(a_{n+1}, \frac{1}{a_{n+1}^2}\right)$とする。
(1)$\frac{a_2}{a_1}$=$\boxed{\ \ あ\ \ }$であり、$\frac{a_3}{a_1}$=$\boxed{\ \ い\ \ }$である。
(2)$a_n$を$a_1$で表すと$a_n$=$\boxed{\ \ う\ \ }$である。無限級数$\displaystyle\sum_{n=1}^{\infty}a_n$の和をTを$a_1$を用いて表すとT=$\boxed{\ \ え\ \ }$である。
(3)$a_1$を正の実数すべてにわたって動かすとき、三角形$A_1A_2A_3$の重心が描く軌跡の方程式をy=f(x)の形で求めるとf(x)=$\boxed{\ \ お\ \ }$となる。
(4)三角形$A_1A_2A_3$が鋭角三角形になるための条件は$\boxed{\ \ か\ \ }$＜$a_1$＜$\boxed{\ \ き\ \ }$である。
(5)x軸上に2点$A'_1$($a_1$, 0), $A'_2$($a_2$, 0)をとり、台形$A_1A_2A'_2A'_1$の面積を$S_1$とする。また、点$A_1$から点$A_3$にいたる曲線Cの部分、および線分$A_3A_2$と$A_2A_1$で囲まれた図形の面積を$S_2$とする。このとき、$S_1$：$S_2$=$\boxed{\ \ く\ \ }$：$\boxed{\ \ け\ \ }$である。ただし、$\boxed{\ \ く\ \ }$と$\boxed{\ \ け\ \ }$は互いに素な自然数である。
2023慶應義塾大学医学部過去問
気付けば一瞬！！ 気付けば爽快！！ 中学数学
三角形を台形として考える 正方形と面積比
図形と計量 三角形の面積 二等分線の利用【烈's study!がていねいに解説】
単元：
#数Ⅰ#数A#図形の性質#図形と計量#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次のような$△ABC$について、$\angle A$の二等分線と辺BCの交点をDとするとき、線分ADの長さを求めよ。
(1)$AB=4、AC=3、A=120°$
(2)$AB=10、AC=15、A=60°$
この動画を見る
次のような$△ABC$について、$\angle A$の二等分線と辺BCの交点をDとするとき、線分ADの長さを求めよ。
(1)$AB=4、AC=3、A=120°$
(2)$AB=10、AC=15、A=60°$
もはやパズル！！三平方の定理禁止！！大阪教育大附属天王寺中
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
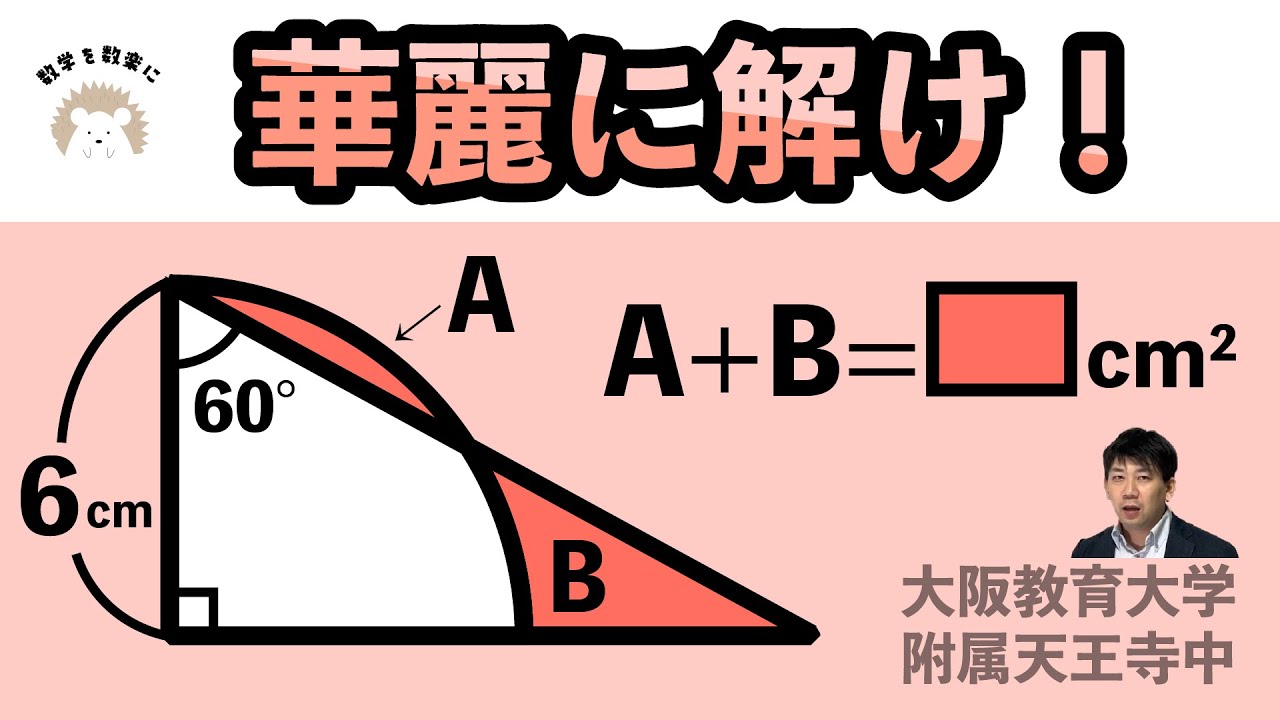
A + B = ▢ ㎠
＊図は動画内参照
大阪教育大学付属天王寺中学校
この動画を見る
A + B = ▢ ㎠
＊図は動画内参照
大阪教育大学付属天王寺中学校
気付けば、知っていれば一瞬！！
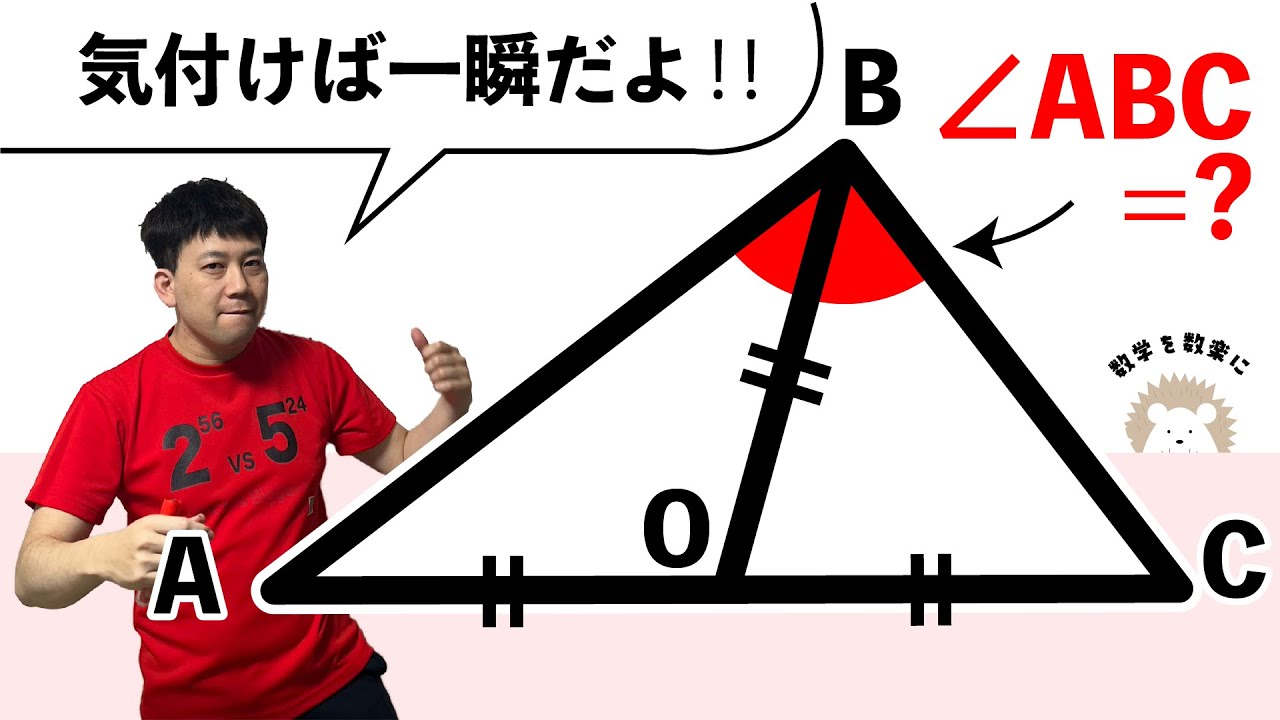
補助線引ける？
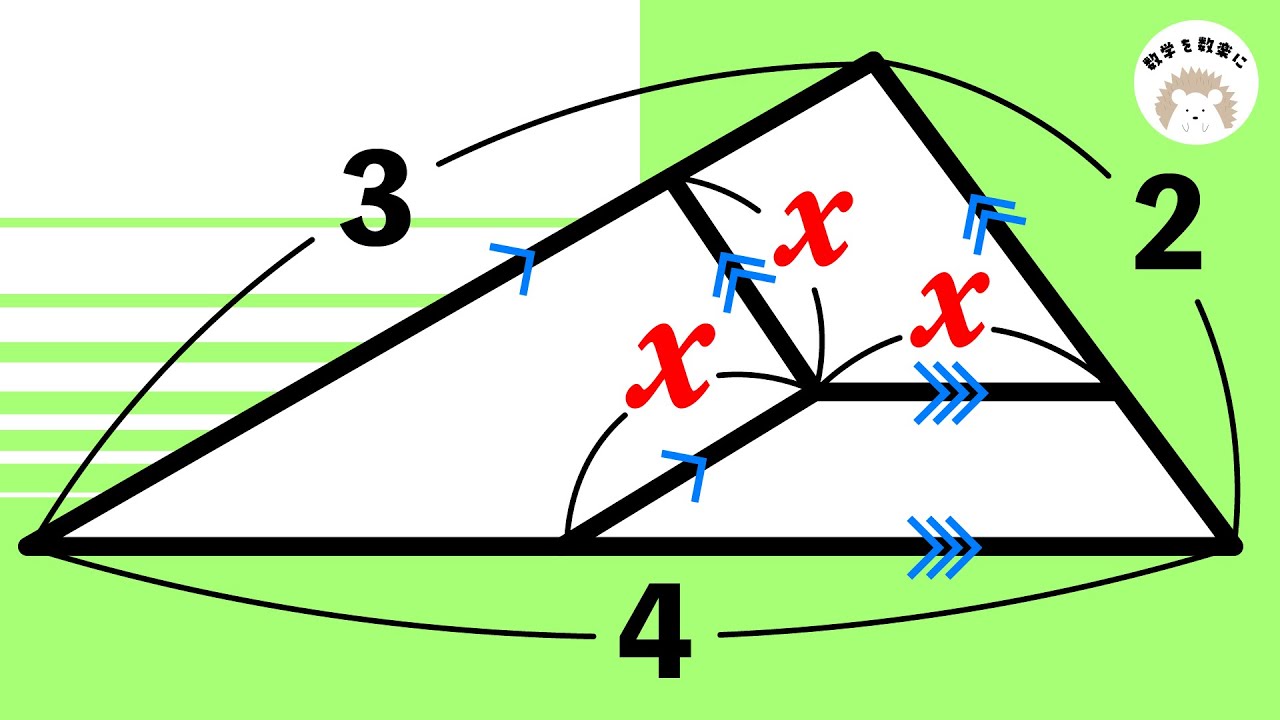
角度を求めよ
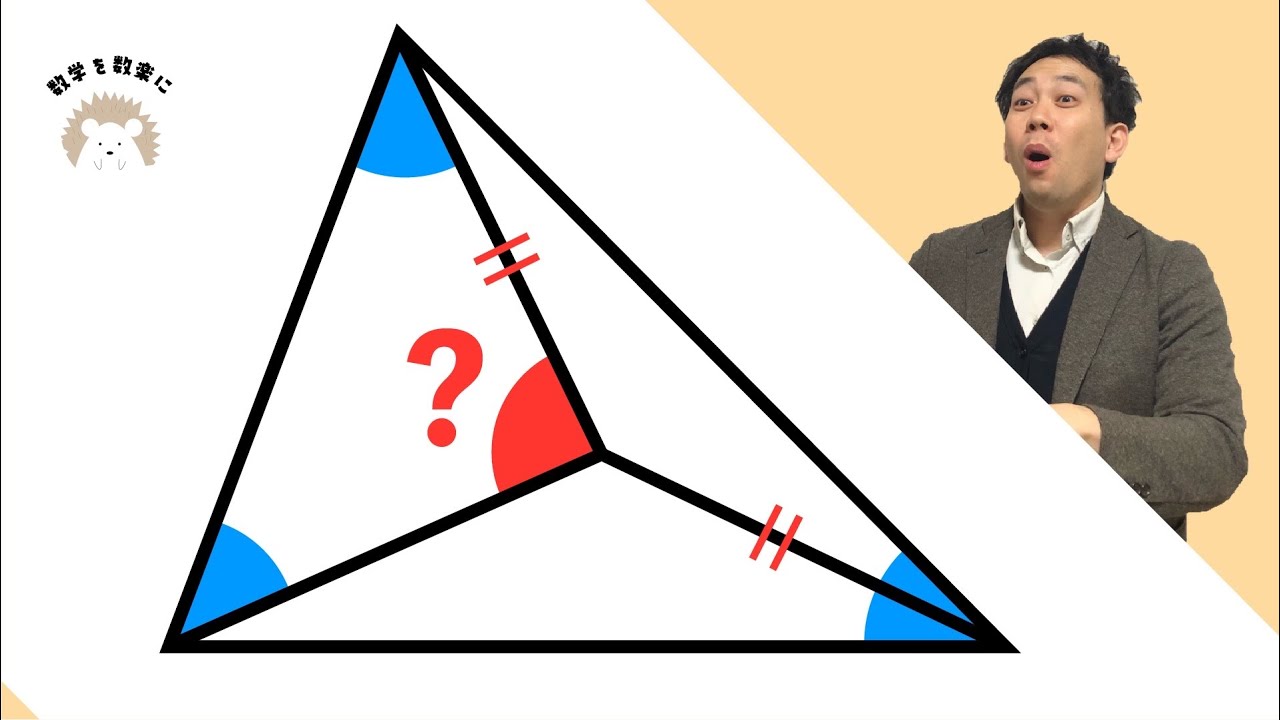
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$\angle OAB = \angle OBA = \angle ACB$
$\angle AOB = ?$
＊図は動画内参照
この動画を見る
$\angle OAB = \angle OBA = \angle ACB$
$\angle AOB = ?$
＊図は動画内参照
黄色の面積＝❓
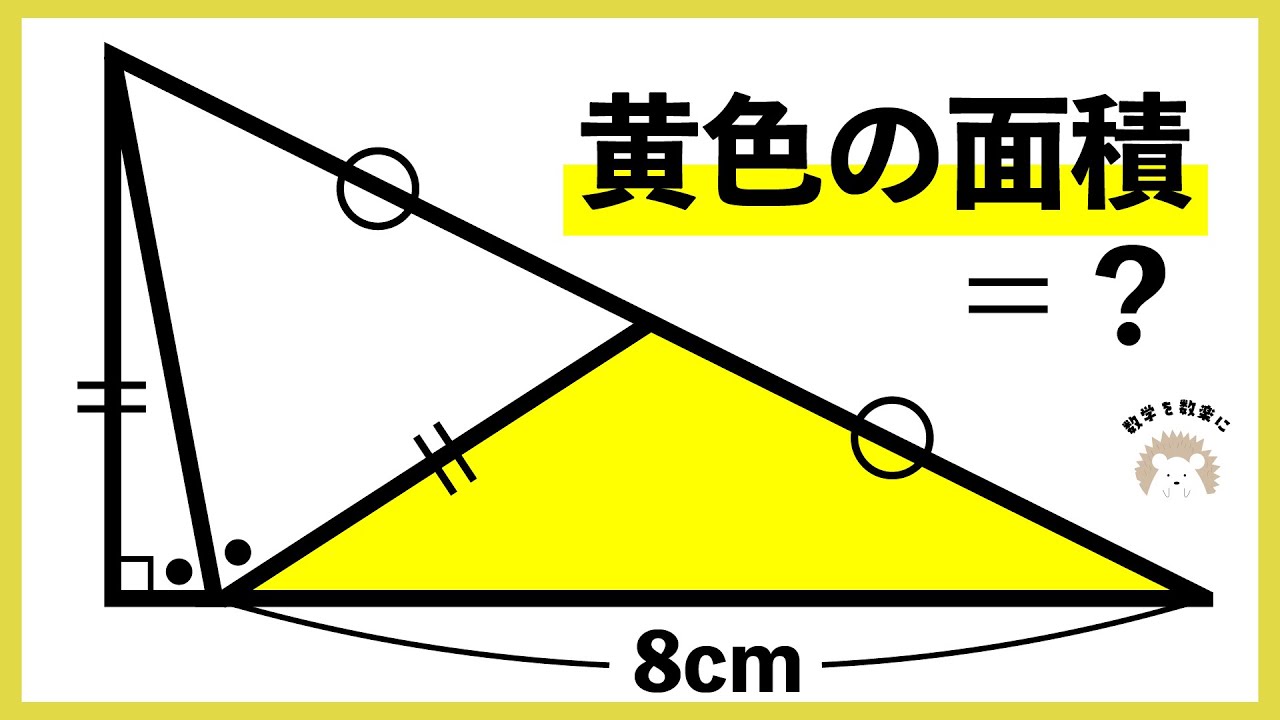
2023年に出題されなかった問題
2023高校入試数学解説97問目 三角形の面積を二等分する直線 宮城県
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
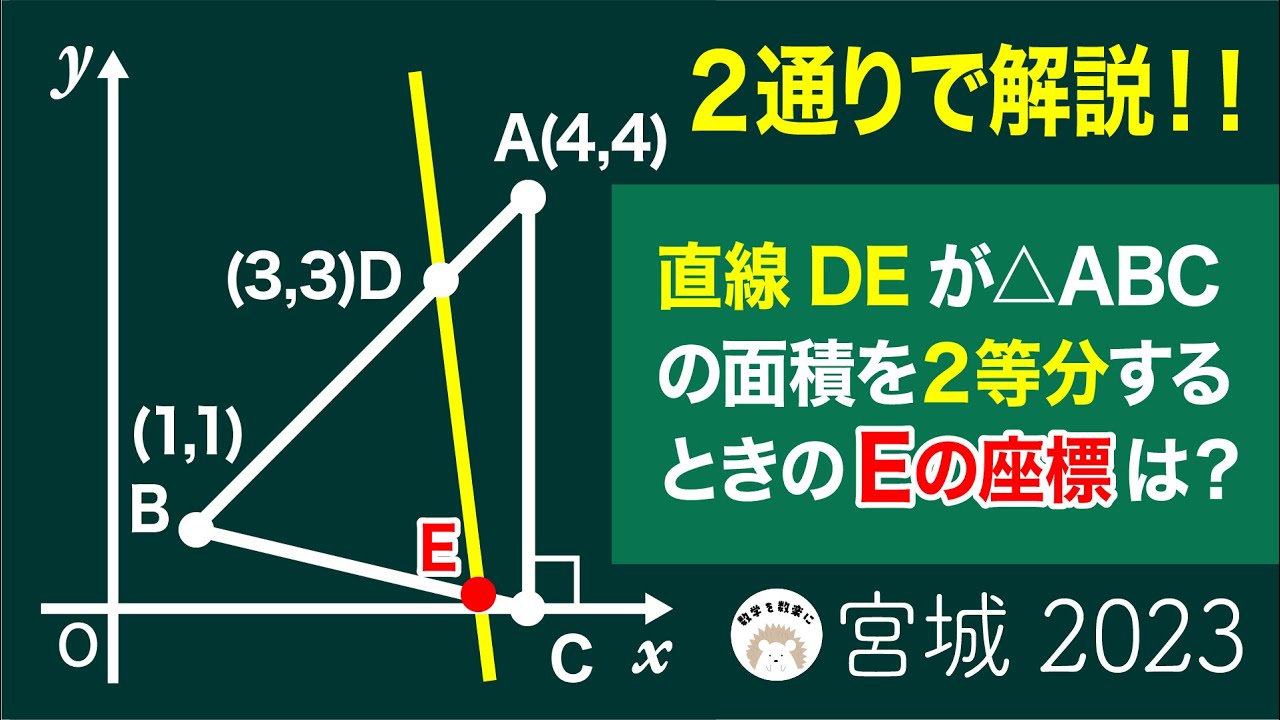
直線DEが△ABCの面積を2等分するときのEの座標は？
＊図は動画内参照
2023宮城県
この動画を見る
直線DEが△ABCの面積を2等分するときのEの座標は？
＊図は動画内参照
2023宮城県
2023高校入試数学解説96問目 直角三角形と角の二等分線 山梨県
2023高校入試数学解説47問目 見えないものを見ようとして 灘高校
単元：
#数学(中学生)#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
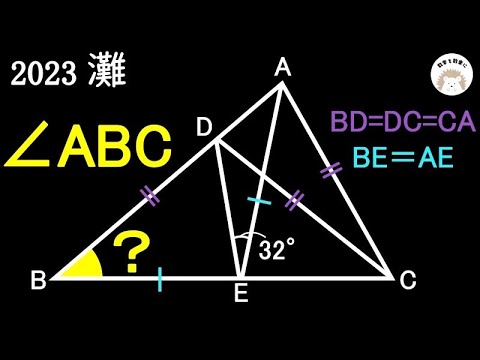
BD=DC=CA
BE=AE
$\angle ABC=?$
＊図は動画内参照
2023 灘高等学校
この動画を見る
BD=DC=CA
BE=AE
$\angle ABC=?$
＊図は動画内参照
2023 灘高等学校
オンライン家庭教師の生徒が開成高校に合格しました！2023高校入試解説41問目 角の二等分線の性質の証明 開成高校（改）
単元：
#数学(中学生)#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
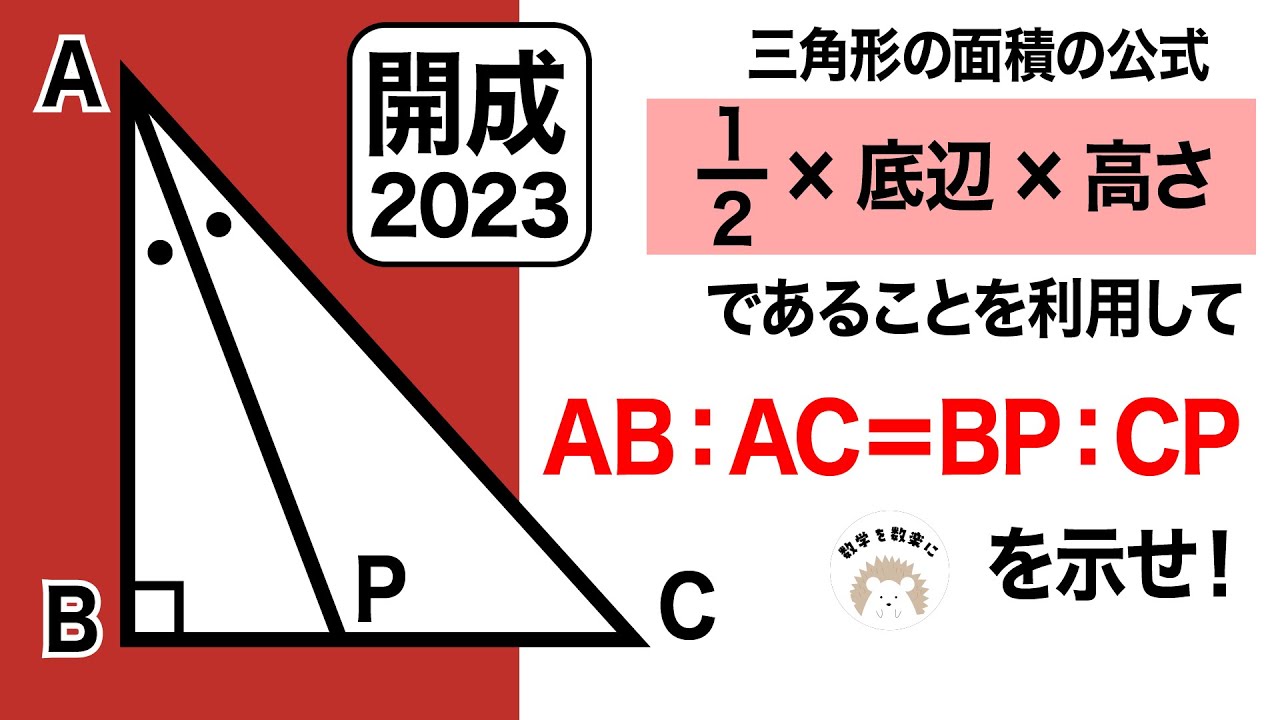
三角形の面積の公式
$\frac{1}{2} \times 底辺 \times 高さ$であることを利用して
AB:AC=BP:CPを示せ
＊図は動画内参照
2023開成高等学校
この動画を見る
三角形の面積の公式
$\frac{1}{2} \times 底辺 \times 高さ$であることを利用して
AB:AC=BP:CPを示せ
＊図は動画内参照
2023開成高等学校
2023高校入試解説28問目 あの条件発動 早稲田本庄
単元：
#数学(中学生)#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
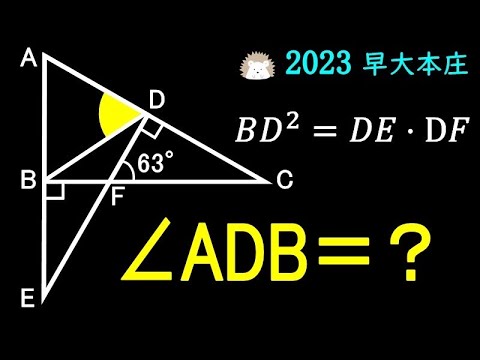
$BD^2 = DE・DF$
$\angle ADB = ?$
＊図は動画内参照
2023早稲田大学 本庄高等学院
この動画を見る
$BD^2 = DE・DF$
$\angle ADB = ?$
＊図は動画内参照
2023早稲田大学 本庄高等学院
放物線と二等辺三角形 国立高専
単元：
#数学(中学生)#中３数学#数A#図形の性質#三平方の定理#三角形の辺の比（内分・外分・二等分線）#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
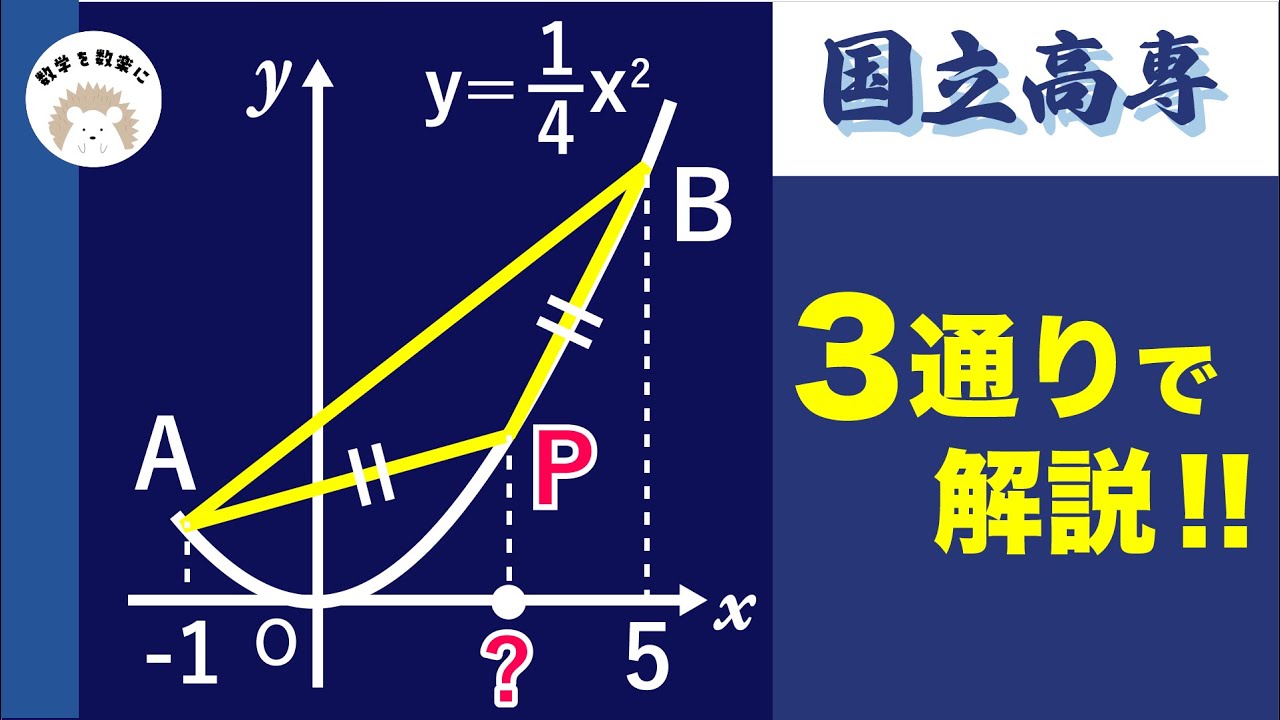
$y=\frac{1}{4}x^2$
P=?
＊図は動画内参照
国立高専
この動画を見る
$y=\frac{1}{4}x^2$
P=?
＊図は動画内参照
国立高専
角の二等分線➕平行線＝❓
2023高校入試解説8問目 内接円 西大和学園 内接円
単元：
#数学(中学生)#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
△ABC∽△PRQ
△PRQ=?
＊図は動画内参照
2023西大和学園高等学校
この動画を見る
△ABC∽△PRQ
△PRQ=?
＊図は動画内参照
2023西大和学園高等学校
2023高校入試解説6問目 座標平面上の正三角形 西大和学園
単元：
#数学(中学生)#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
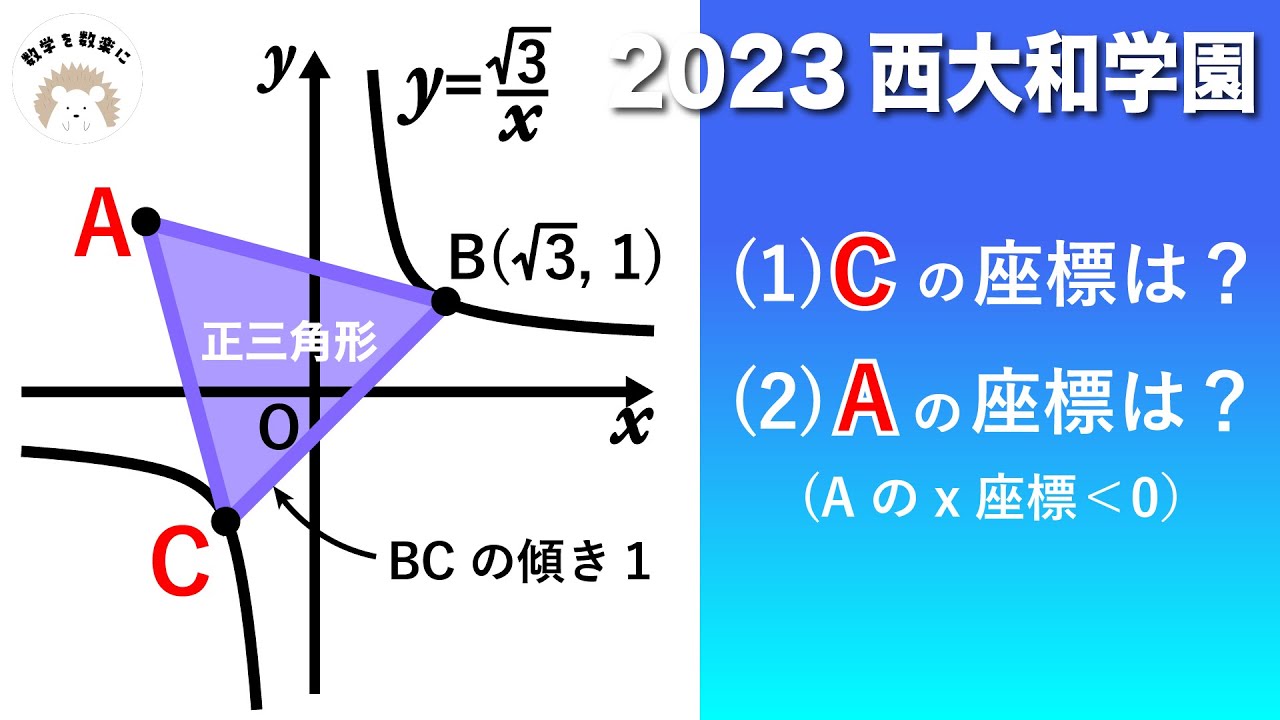
(1)Cの座標は？
(2)Aの座標は？
(Aのx座標＜0)
＊図は動画内参照
2023西大和学園高等学校
この動画を見る
(1)Cの座標は？
(2)Aの座標は？
(Aのx座標＜0)
＊図は動画内参照
2023西大和学園高等学校
面積二等分する直線を選べ！！大阪府
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
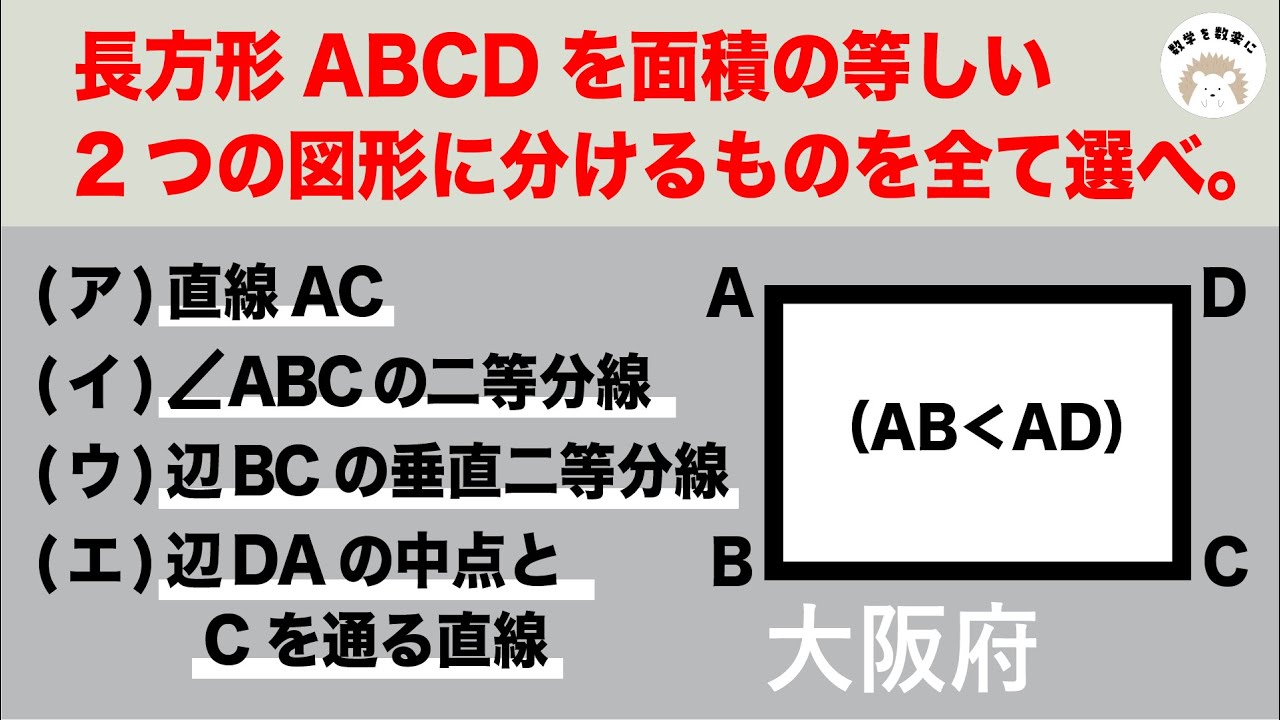
長方形ABCDを面積の等しい2つの図形に分けるものを全て選べ。
(ア)直線AC
(イ)$\angle ABC$の二等分線
(ウ)辺BCの垂直二等分線
(エ)辺DAの中点とCを通る直線
＊図は動画内参照
大阪府
この動画を見る
長方形ABCDを面積の等しい2つの図形に分けるものを全て選べ。
(ア)直線AC
(イ)$\angle ABC$の二等分線
(ウ)辺BCの垂直二等分線
(エ)辺DAの中点とCを通る直線
＊図は動画内参照
大阪府
面積比やら三平方の定理やら。。良問！！慶應志木
単元：
#数学(中学生)#中３数学#数A#図形の性質#三平方の定理#三角形の辺の比（内分・外分・二等分線）#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
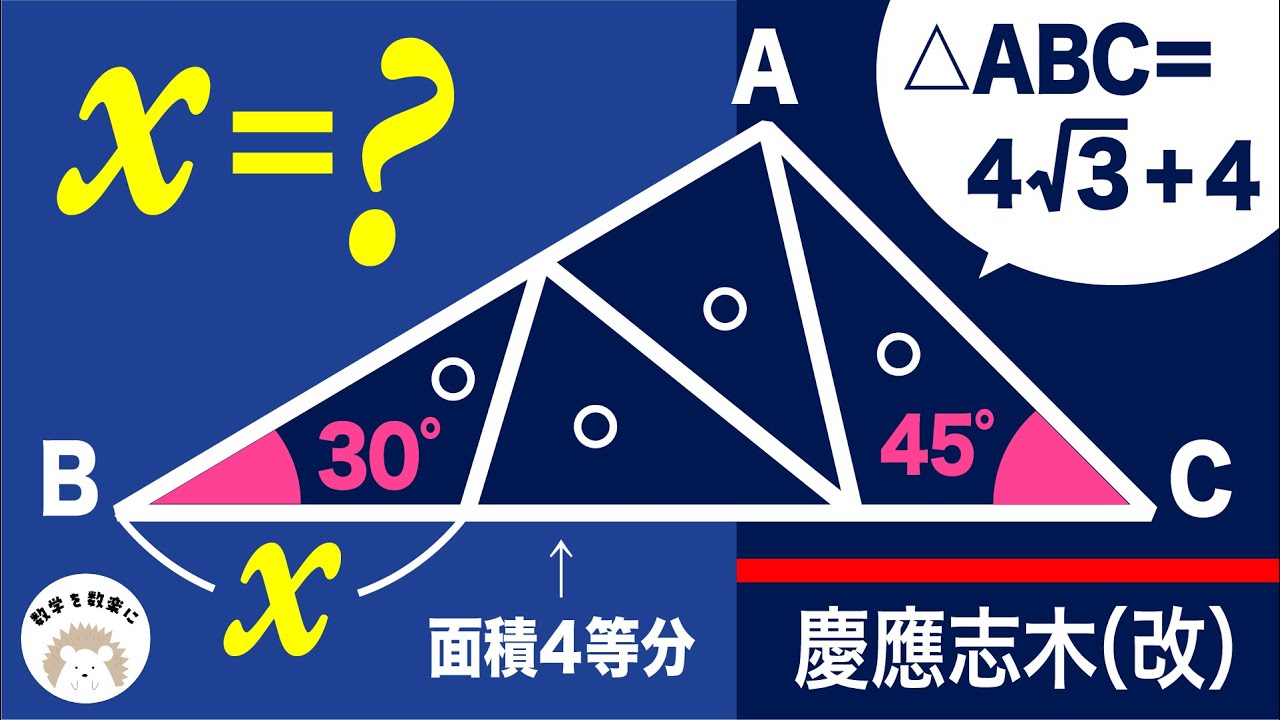
面積4等分
$△ABC=4 \sqrt 3 +4$
x=?
＊図は動画内参照
慶應義塾志木高等学校（改）
この動画を見る
面積4等分
$△ABC=4 \sqrt 3 +4$
x=?
＊図は動画内参照
慶應義塾志木高等学校（改）
面積から辺への引越し 慶應志木
単元：
#数学(中学生)#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
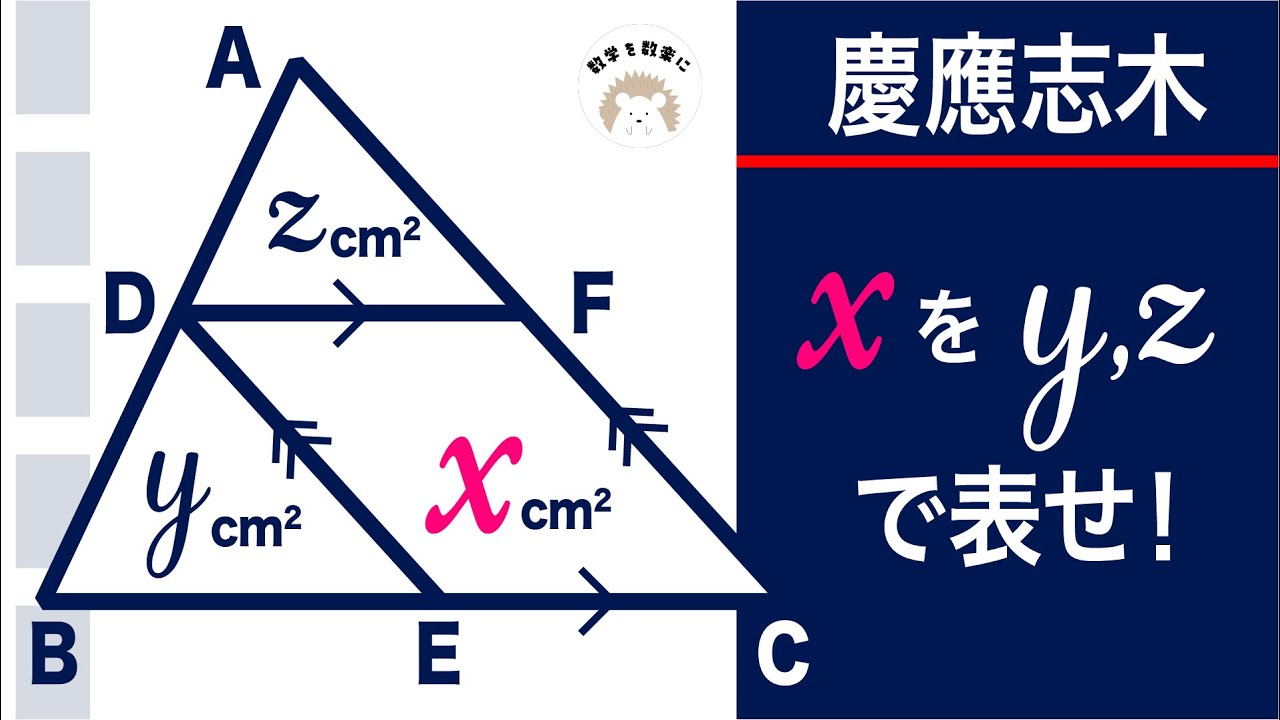
xをy,zで表せ
＊図は動画内参照
慶應義塾志木高等学校
この動画を見る
xをy,zで表せ
＊図は動画内参照
慶應義塾志木高等学校
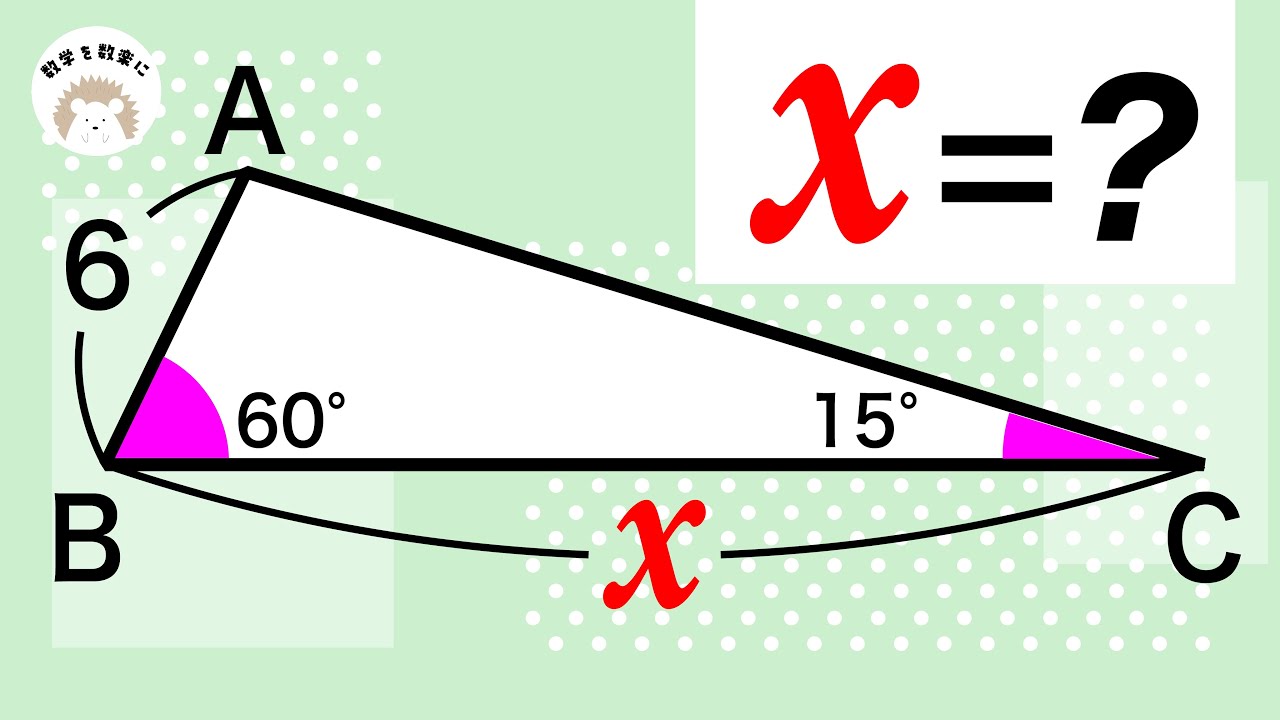
見た目は難問！？直角三角形に関する問題
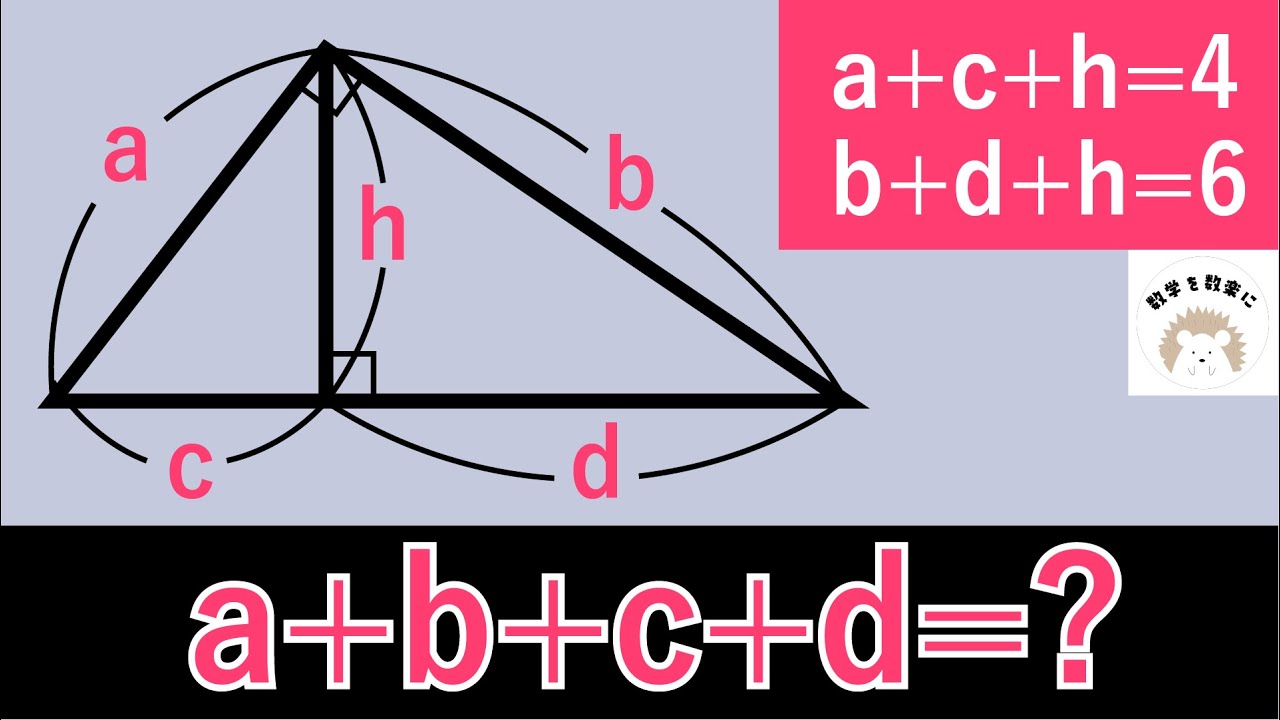
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
a+c+h = 4
b+d+h = 6
a+b+c+d =?
＊図は動画内参照
この動画を見る
a+c+h = 4
b+d+h = 6
a+b+c+d =?
＊図は動画内参照
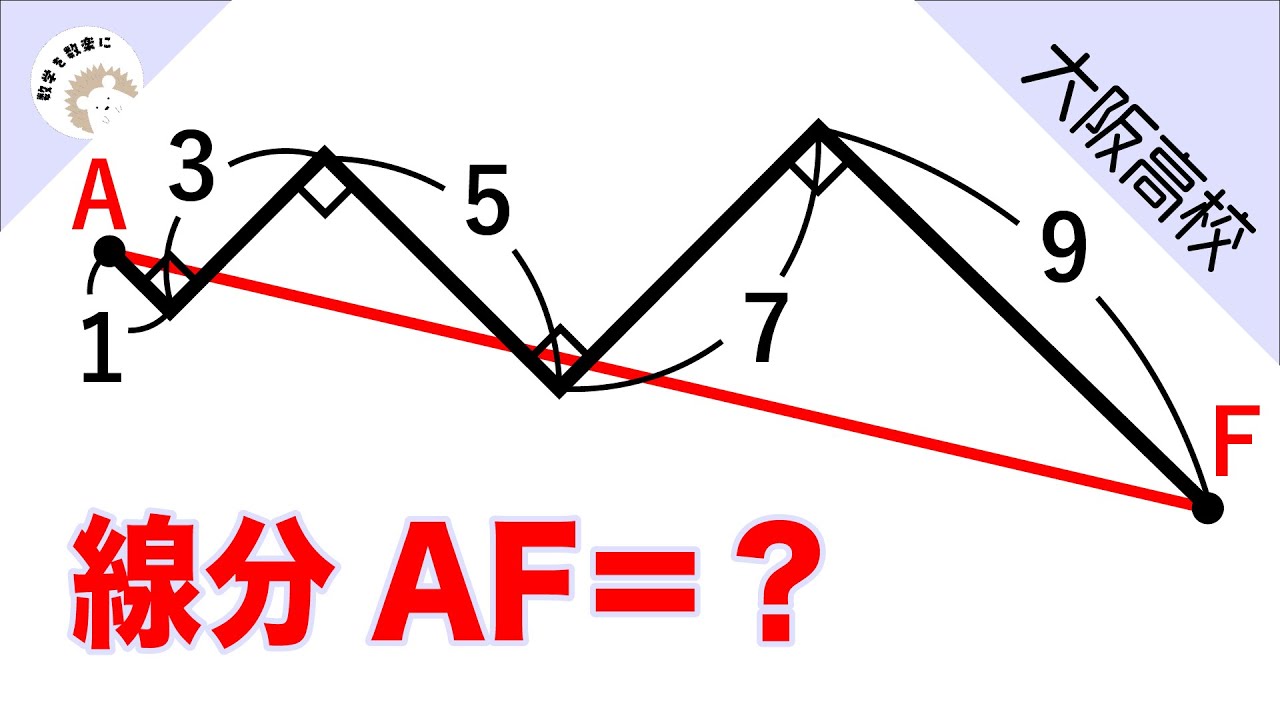
ジグザグ 大阪高校
単元：
#数学(中学生)#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
線分AF=?
＊図は動画内参照
大阪高等学校
この動画を見る
線分AF=?
＊図は動画内参照
大阪高等学校
補助線引けるかな？
関数の問題にみえて実は○形の問題 中央大杉並
単元：
#数学(中学生)#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
a=?
＊図は動画内参照
中央大学杉並高等学校
この動画を見る
a=?
＊図は動画内参照
中央大学杉並高等学校
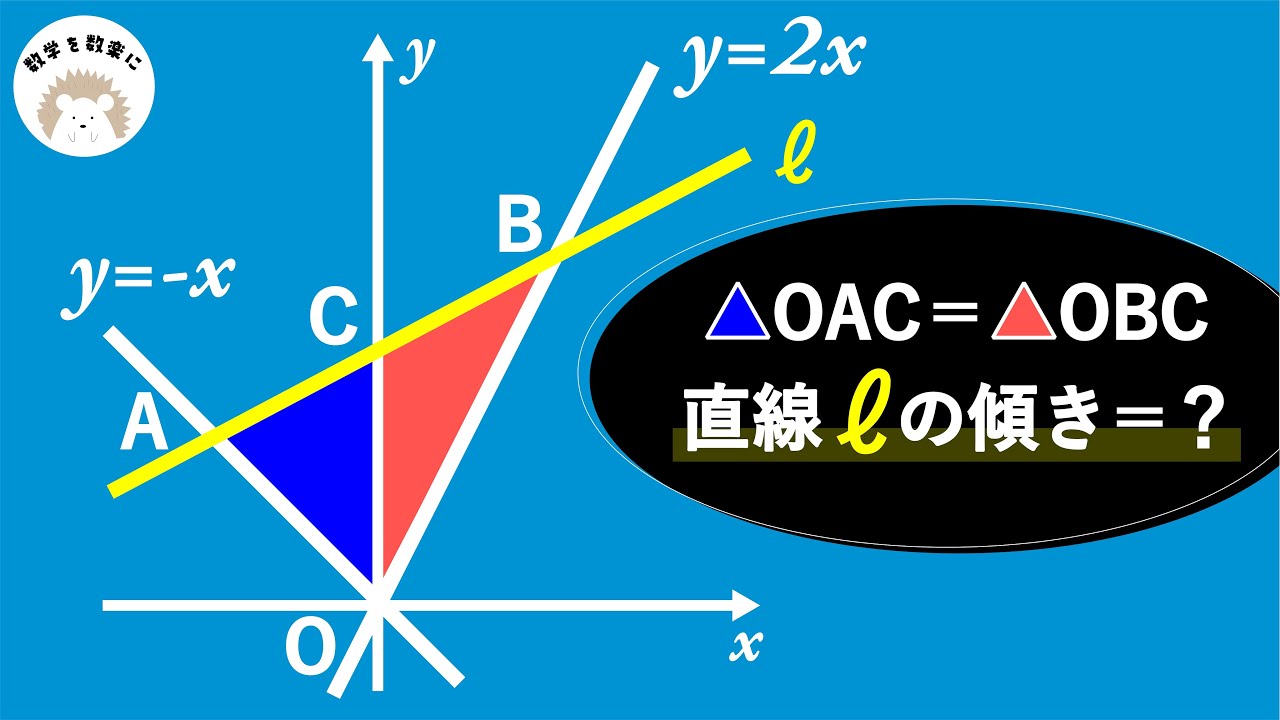
モジモジしてないで文字でおけ！！関数
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
△OAC＝△OBC
直線lの傾き=?
＊図は動画内参照
この動画を見る
△OAC＝△OBC
直線lの傾き=?
＊図は動画内参照
直角の角の二等分線からできるもの 専大松戸
角度を求める問題
