問題文全文(内容文)：
198
△ABCの内接円が辺BC,CA, AB と接する点を
それぞれD,E, Fとする。BC=a, CA=b, AB=c とし
△ABC の内接円の半径をrとするとき
次の問いに答えよ。
(1) 線分 BD, CE, AFの長さをa,b,cを用いて表せ。
(2) △ABC の面積をa,b,c,rを用いて表せ。
(3) a=5,b=3,c=4 のとき,rの値を求めよ。

193
鋭角三角形ABCの頂点Aから
BCに下ろした垂線をAD とし
Dから AB, ACに下ろした垂線
をそれぞれDE,DF とするとき
四角形BCFE は円に内接すること
を証明せよ。

問題文全文(内容文)：
191
右の図のように，AB=AC である二等辺三角形ABCの外接円Oの弧 BC 上に点Dをとり、線分
DCのCを越える延長上に BD=CE となる点Eをとる。このとき、△ADE は二等辺三角形であることを証明せよ。

192
鋭角三角形ABCにおいて，辺BC, CA,ABの中点を、それぞれD,E, Fとすると，△AFE,△ BDF, △CED の外接円は，どれもAABCの外心Oを通ることを証明せよ。

問題文全文(内容文)：
188 円oにおいて、平行な2つの弦をAA´、BB´とし、AB´とA´Bが円の内部の点Pで交わっている。このとき、∠APB＝∠AOBであることを証明せよ。
189 鋭角三角形ABCの垂心をHとし、AHがBCと交わる点をD、△ABCの外接円と交わる点をEとする。このとき、Dは線分HEの中点であることを証明せよ。
190下の図において、角θを求めよ。

問題文全文(内容文)：
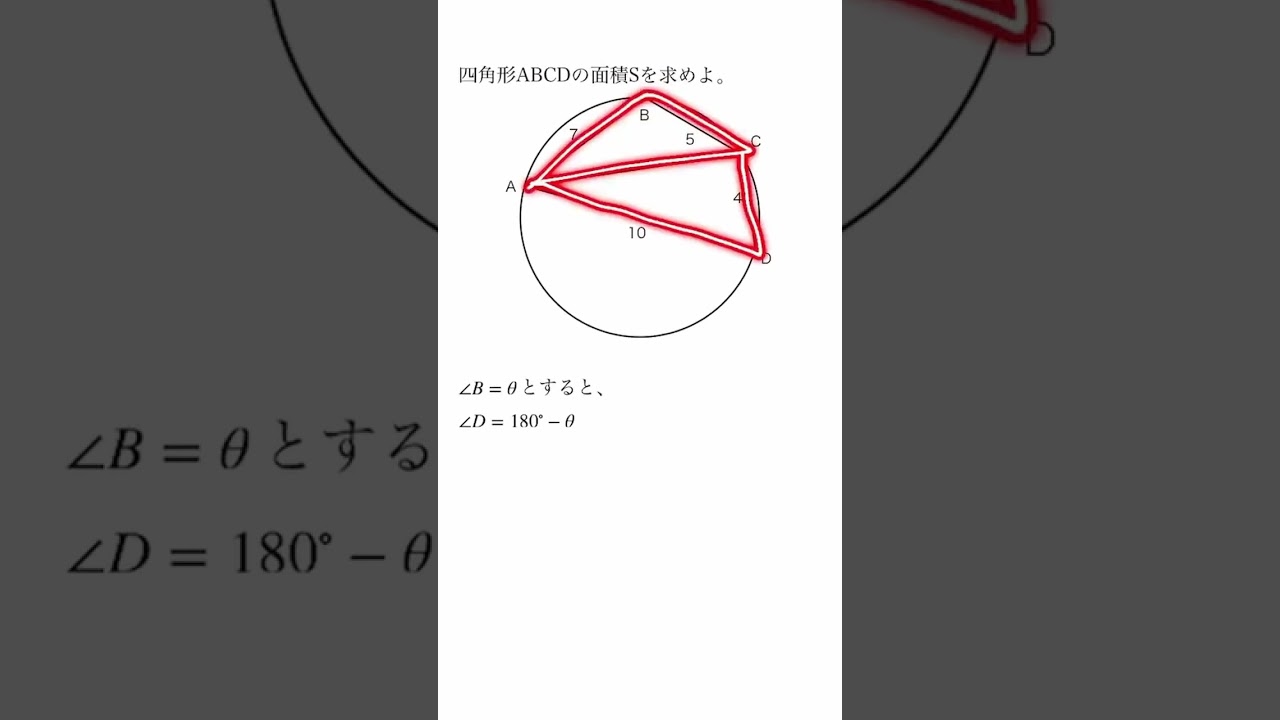
四角形$ABCD$の面積$S$を求めよ。

問題文全文(内容文)：
正八面体とその内接球の半径の出し方とその過程における注意点を解説！