問題文全文(内容文)：
${\Large\boxed{1}}$　
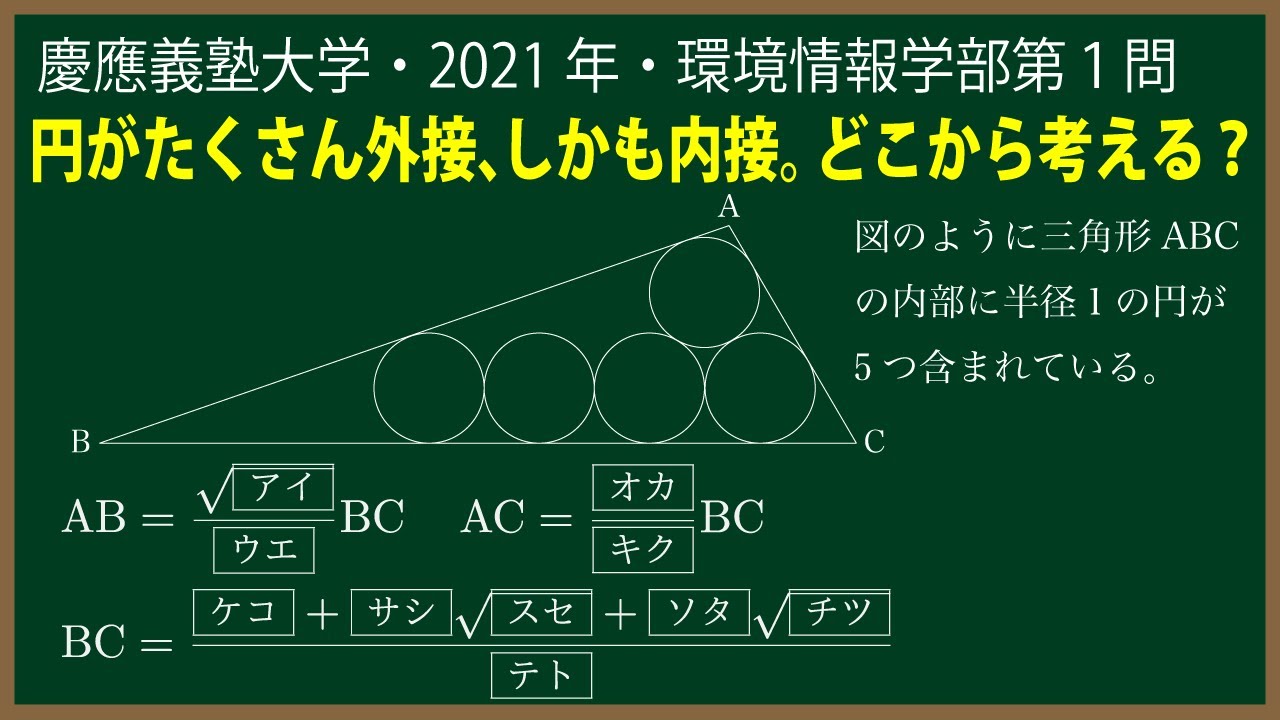
図(※動画参照)のように三角形$\rm ABC$の内部に半径$1$の円が5つ含まれている。4つの円は辺$\rm BC$に接しながら横一列に互いに接しながら並び、左端の円は辺$\rm AB$に接し、右端の円は辺$\rm AC$に接している。また、もう一つの円は、辺$\rm AB$と辺$\rm AC$に接し、4つの円の右側の2つの円に接している。このとき
$\textrm{AB}=\dfrac{\sqrt{\boxed{\ \ アイ\ \ }}}{\boxed{\ \ ウエ\ \ }}\textrm{BC}$　
$\rm AC=\dfrac{\boxed{\ \ オカ\ \ }}{\boxed{\ \ キク\ \ }}BC$
$\rm BC=\dfrac{1}{\boxed{\ \ テト\ \ }}(\boxed{\ \ ケコ\ \ }+$$\boxed{\ \ サシ\ \ }\sqrt{\boxed{\ \ スセ\ \ }}+$$\boxed{\ \ ソタ\ \ }\sqrt{\boxed{\ \ チツ\ \ }})$　　　$(\boxed{\ \ スセ\ \ } \lt \boxed{\ \ チツ\ \ })$
である。

2021慶應義塾大学環境情報学部過去問

問題文全文(内容文)：
△ABCにおいて、$AB=3,AC=6,\angle BAC=90°$であるとき、$BC=(ア)\sqrt{(イ)}$である。Aを中心とし、Bを通る円をKとし、円Kと直線ACの交点のうち辺AC上にある方をD、もう一方をEとする。また、円Kと直線BCの交点でBと異なるものをFとする。このとき、CE=(ウ)であり、方べきの定理を用いると、$CF=\dfrac{(エ)\sqrt{(オ)}}{(カ)}$とわかるから$\dfrac{BF}{FC}=\dfrac{(キ)}{(ク)}$である。さらに、直線EFと辺ABの交点をP、直線EFと線分BCの交点をQとすると、$\dfrac{BQ}{QD}=(ケ)$であり、△BFQの面積は$\dfrac{(コ)}{(サシ)}$である。また、△CPQの面積は$\dfrac{(ス)}{(セ)}$である。

問題文全文(内容文)：
$\triangle ABC$に対し、点$P$辺$AB$の中点、点$Q$は辺$BC$上の$B,C$と異なる点、点$R$は直線$AQ$と直線$CP$との交点とする。
このとき、各問いに答えよ。
（1）
$a=\displaystyle \frac{CR}{RP},b=\displaystyle \frac{CQ}{QB}$とおくとき、$a$と$b$の関係式を求めよ。

（2）
$\triangle ABC$の外接円$O$と直線$CP$との点$C$以外の交点を$X$とする。
$AP=CR,CQ=QB$であるとき、$CR:RP:PX$を求めよ。

問題文全文(内容文)：
2つの円の半径の和=47,2つの円の半径の差=43のとき
斜線部の面積=?
＊図は動画内参照

問題文全文(内容文)：
大円の半径を1とする.
2つの半円の面積の和を求めよ.

問題文全文(内容文)：
${\large第5問}$
$\triangle ABC$において、$AB=3$,　$BC=4$,　$AC=5$とする。
$\angle BAC$の二等分線と辺$BC$との交点を$D$とすると
$BD=\displaystyle \frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$,　$AD=\displaystyle \frac{\boxed{\ \ ウ\ \ }\sqrt{\boxed{\ \ エ\ \ }}}{\boxed{\ \ オ\ \ }}$
である。
また、$\angle BAC$の二等分線と$\triangle ABC$の外接円$O$との交点で点$A$とは異なる
点を$E$とする。$\triangle AEC$に着目すると
$AE=\boxed{\ \ カ\ \ }\sqrt{\boxed{\ \ キ\ \ }}$
である。
$\triangle ABC$の2辺$AB$と$AC$の両方に接し、外接円$O$に内接する円の中心を
$P$とする。円$P$の半径を$r$とする。さらに、円$P$と外接円$O$との接点を
$F$とし、直線$PF$と外接円$O$との交点で点$F$とは異なる点を$G$とする。
このとき
$AP=\sqrt{\boxed{\ \ ク\ \ }}\ r$,　$PG=\boxed{\ \ ケ\ \ }-r$
と表せる。したがって、方べきの定理により$r=\displaystyle \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。

$\triangle ABC$の内心を$Q$とする。内接円$Q$の半径は$\boxed{\ \ シ\ \ }$で、$AQ=\sqrt{\boxed{\ \ ス\ \ }}$
である。また、円$P$と辺$AB$との接点を$H$とすると、$AH=\displaystyle \frac{\boxed{\ \ セ\ \ }}{\boxed{\ \ ソ\ \ }}$である。
以上から、点$H$に関する次の$(\textrm{a}),(\textrm{b})$の正誤の組合せとして正しいもの
は$\boxed{\boxed{\ \ タ\ \ }}$である。


$(\textrm{a})$点$H$は3点$B,D,Q$を通る円の周上にある。
$(\textrm{b})$点$H$は3点$B,E,Q$を通る円の周上にある。

$\boxed{\boxed{\ \ タ\ \ }}$の解答群
(※選択肢は動画参照)

2021共通テスト過去問

問題文全文(内容文)：
${\large第5問}$
$\triangle ABC$において、辺$BC$を$7:1$に内分する点を$D$とし、辺$AC$を$7:1$に
内分する点を$E$とする。線分$AD$と線分$BE$の交点を$F$とし、直線$CF$
と辺$AB$の交点を$G$とすると

$\displaystyle \frac{GB}{AG}=\boxed{\ \ ア\ \ },　\displaystyle \frac{FD}{AF}=\displaystyle \frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }},$$　\displaystyle \frac{FC}{GF}=\displaystyle \frac{\boxed{\ \ エ\ \ }}{\boxed{\ \ オ\ \ }}$

である。したがって

$\displaystyle \frac{\triangle CDGの面積}{\triangle BFGの面積}=\displaystyle \frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キク\ \ }}\displaystyle$

となる。

4点$B,D,F,G$が同一円周上にあり、かつ$FD=1$のとき

$AB=\boxed{\ \ ケコ\ \ }$

である。さらに、$AE=3\sqrt7$とするとき、$AE・AC=\boxed{\ \ サシ\ \ }$であり

$\angle AEG=\boxed{\ \ ス\ \ }$

である。$\boxed{\ \ ス\ \ }$に当てはまるものを、次の⓪～③のうちから一つ選べ。
⓪$\angle BGE$
①$\angle ADB$
②$\angle ABC$
③$\angle BAD$

2020センター試験過去問

問題文全文(内容文)：
共通内接線の解説動画です

問題文全文(内容文)：
【高校数学】方べきの定理の証明について解説動画です

問題文全文(内容文)：
①2つの円が点$A$で同じ直線に接している.
この直線上の$A$と異なる点$B$を通る2本の直線と,
2円との2つの交点をそれぞれ$C,D$および$E,F$とする.
このとき,4点$C,D,E,F$は同一円周上にあることを証明しよう.

図は動画内参照

問題文全文(内容文)：
①半径上の円に内接する四角形$ABCD$において,
辺$BC$がこの円の直径である.
対角線$AC$と$BD$の交点を$E$とし,$E$から$BC$に垂線$EF$を下ろす.
$BF:FC=m: n$とするとき,$BE･BD$を$r,m,n$を用いて表そう.

図は動画内参照

問題文全文(内容文)：
点Pを通る2直線が,円$O$とそれそれ 2点$A,B$と
2点$C,D$で交わるとき,$①=①$が成り立つ.

点$P$を通る2直線の一方が,
円$O$と2点$A,B$で交わり,もう一方が点$T$で接するとき,
$②=②$が成り立つ.

下の図で$x$を求めよう.
ただし,$T$は接点とする.

③

④

図は動画内参照

問題文全文(内容文)：
三角形の1つの①の①と,他の2つの頂点における
②の②は1点で交わる.この点を傍心という.

③$\triangle ABC$の頂点$A$における内角の二等分線と直線$B,C$
それぞれにおける外角の二等分線は1点で交わることを証明しよう.

図は動画内参照