 確率分布
確率分布
 確率分布
確率分布
【数B】確率分布と統計的推測:正規分布表の見方と暗記すべき数字を説明します!

【数B】確率分布と統計的推測:正規分布を使って上位何人目か考えてみよう!

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
1学年600人の生徒が数学Bのテストを受けた。
母集団がN(60,25)に従うとき、70点を取った生徒は上位何番目?
標準正規分布を用いて求めよう!正規分布表を使います。
この動画を見る
1学年600人の生徒が数学Bのテストを受けた。
母集団がN(60,25)に従うとき、70点を取った生徒は上位何番目?
標準正規分布を用いて求めよう!正規分布表を使います。
【数B】確率分布:<分散の計算に注意!>2つの確率変数の和の期待値・分散

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
(2つの確率の和の期待値・分散の求め方と例)
赤のコイン2枚投げて表の出た枚数をX,青のコイン1枚投げて表の出た枚数をYとするとき、X+Yの期待値・分散を求めよう
この動画を見る
(2つの確率の和の期待値・分散の求め方と例)
赤のコイン2枚投げて表の出た枚数をX,青のコイン1枚投げて表の出た枚数をYとするとき、X+Yの期待値・分散を求めよう
【数B】確率分布:変量の変換公式 こう覚えておけばOK!

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
XからYに確率変数を$Y=aX+b$で変換する場合の期待値、分散、標準偏差の公式
この動画を見る
XからYに確率変数を$Y=aX+b$で変換する場合の期待値、分散、標準偏差の公式
【数B】確率分布:確率分布表から分散を求めよう!

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
確率変数Xが,X=0,1,2にあたる確率を1/6,1/3,1/2としたとき、分散V(X)の値
この動画を見る
確率変数Xが,X=0,1,2にあたる確率を1/6,1/3,1/2としたとき、分散V(X)の値
【数B】確率分布:期待値の計算と意味をコンパクトに教えます!

【数B】確率分布:確率変数と確率分布を基本から解説します!!

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
確率変数と確率分布を基本から解説します!!
サイコロ1回振ったとき、確率分布表を書いてみましょう!
この動画を見る
確率変数と確率分布を基本から解説します!!
サイコロ1回振ったとき、確率分布表を書いてみましょう!
血液型ガチャ 愛知医科大

単元:
#確率分布と統計的な推測#確率分布#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
血液型$AB$の割合を$10$%とする.
$\Box$人以上集めればその中に少なくとも1人以上$AB$型がいる確率が$99$%以上となる.
$\Box$を求めよ.
この動画を見る
血液型$AB$の割合を$10$%とする.
$\Box$人以上集めればその中に少なくとも1人以上$AB$型がいる確率が$99$%以上となる.
$\Box$を求めよ.
共通テスト第2日程2021年数学詳しい解説〜共通テスト第2日程2021年2B第3問〜確率分布と統計

単元:
#大学入試過去問(数学)#確率分布と統計的な推測#確率分布#センター試験・共通テスト関連#共通テスト#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\large第3問}$
ある大学には、多くの留学生が在籍している。この大学の留学生に対して学習や生活を支援する
留学生センターでは、留学生の日本語の学習状況について関心を寄せている。
(1)この大学では、留学生に対する授業として、いかに示す三つの日本語学習コースがある。
初級コース:1週間に10時間の日本語の授業を行う
中級コース:1週間に8時間の日本語の授業を行う
上級コース:1週間に6時間の日本語の授業を行う
すべての留学生が三つのコースのうち、いずれか一つのコースのみに登録する
ことになっている。留学生全体における各コースに登録した留学生の割合は、
それぞれ 初級コース:20%, 中級コース:35%, 上級コース:$\boxed{\ \ アイ\ \ }%$
であった。ただし、数値はすべて正確な値であり、四捨五入されていないものとする。
この留学生の集団において、一人を無作為に抽出したとき、その留学生が1週間に
受講する日本語学習コースの授業の時間数を表す確率変数をXとする。
$X$の平均(期待値)は$\displaystyle \frac{\boxed{\ \ ウエ\ \ }}{2}$であり、$X$の分散は$\displaystyle \frac{\boxed{\ \ オカ\ \ }}{20}$である。
次に、留学生全体を母集団とし、$a$人を無作為に抽出した時、初級コースに登録した人数
を表す確率変数を$Y$とすると、$Y$は二項分布に従う。このとき、$Y$の平均$E(Y)$は
$E(Y)=\displaystyle \frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}$
である。
また、上級コースに登録した人数を表す確率変数を$Z$とすると、$Z$は二項分布に従う。
$Y,Z$の標準偏差をそれぞれ$\delta(Y),\delta(Z)$とすると
$\displaystyle \frac{\delta(Z)}{\delta(Y)}=\displaystyle \frac{\boxed{\ \ ケ\ \ }\sqrt{\boxed{\ \ コサ\ \ }}}{\boxed{\ \ シ\ \ }}$
である。
ここで、$a=100$としたとき、無作為に抽出された留学生のうち、初級コースに
登録した留学生が28人以上となる確率を$p$とする。$a=100$は十分大きいので、
$Y$は近似的に正規分布に従う。このことを用いて$p$の近似値を求めると、
$p=\boxed{\boxed{\ \ ス\ \ }}$である。
$\boxed{\boxed{\ \ ス\ \ }}$については。最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪$0.002$ ①$0.023$ ②$0.228$ ③$0.477$ ④$0.480$ ⑤$0.977$
(2)40人の留学生を無作為に抽出し、ある1週間における留学生の日本語学習コース
以外の日本語の学習時間(分)を調査した。ただし、日本語の学習時間は母平均$m$,
母分散$\delta^2$の分布に従うものとする。
母分散$\delta^2$を$640$と仮定すると、標本平均の標準偏差は$\boxed{\ \ セ\ \ }$となる。
調査の結果、40人の学習時間の平均値は120であった。標本平均が近似的に
正規分布に従うとして、母平均$m$に対する信頼度95%の信頼区間を$C_1 \leqq m \leqq C_2$とすると
$C_1=\boxed{\ \ ソタチ\ \ }.\boxed{\ \ ツテ\ \ },$
$C_2=\boxed{\ \ トナニ\ \ }.\boxed{\ \ ヌネ\ \ }$
である。
(3)(2)の調査とは別に、日本語の学習時間を再度調査することになった。そこで、
50人の留学生を無作為に抽出し、調査した結果、学習時間の平均値は120であった。
母分散$\delta^2$を640と仮定したとき、母平均$m$に対する信頼度95%の信頼区間を
$D_1 \leqq m \leqq D_2$とすると、$\boxed{\boxed{\ \ ノ\ \ }}$が成り立つ。
一方、母分散$\delta^2$を960と仮定したとき、母平均$m$に対する信頼度95%の
信頼区間を$E_1 \leqq m \leqq E_2$とする。このとき、$D_2-D_1=E_2-E_1$と
なるためには、標本の大きさを50の$\boxed{\ \ ハ\ \ }.\boxed{\ \ ヒ\ \ }$倍にする必要がある。
$\boxed{\boxed{\ \ ノ\ \ }}$の解答群
⓪$D_1 \lt C_1$かつ$D_2 \lt C_2$ ①$D_1 \lt C_1$かつ$D_2 \gt C_2$
②$D_1 \gt C_1$かつ$D_2 \lt C_2$ ③$D_1 \gt C_1$かつ$D_2 \gt C_2$
2021共通テスト過去問
この動画を見る
${\large第3問}$
ある大学には、多くの留学生が在籍している。この大学の留学生に対して学習や生活を支援する
留学生センターでは、留学生の日本語の学習状況について関心を寄せている。
(1)この大学では、留学生に対する授業として、いかに示す三つの日本語学習コースがある。
初級コース:1週間に10時間の日本語の授業を行う
中級コース:1週間に8時間の日本語の授業を行う
上級コース:1週間に6時間の日本語の授業を行う
すべての留学生が三つのコースのうち、いずれか一つのコースのみに登録する
ことになっている。留学生全体における各コースに登録した留学生の割合は、
それぞれ 初級コース:20%, 中級コース:35%, 上級コース:$\boxed{\ \ アイ\ \ }%$
であった。ただし、数値はすべて正確な値であり、四捨五入されていないものとする。
この留学生の集団において、一人を無作為に抽出したとき、その留学生が1週間に
受講する日本語学習コースの授業の時間数を表す確率変数をXとする。
$X$の平均(期待値)は$\displaystyle \frac{\boxed{\ \ ウエ\ \ }}{2}$であり、$X$の分散は$\displaystyle \frac{\boxed{\ \ オカ\ \ }}{20}$である。
次に、留学生全体を母集団とし、$a$人を無作為に抽出した時、初級コースに登録した人数
を表す確率変数を$Y$とすると、$Y$は二項分布に従う。このとき、$Y$の平均$E(Y)$は
$E(Y)=\displaystyle \frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}$
である。
また、上級コースに登録した人数を表す確率変数を$Z$とすると、$Z$は二項分布に従う。
$Y,Z$の標準偏差をそれぞれ$\delta(Y),\delta(Z)$とすると
$\displaystyle \frac{\delta(Z)}{\delta(Y)}=\displaystyle \frac{\boxed{\ \ ケ\ \ }\sqrt{\boxed{\ \ コサ\ \ }}}{\boxed{\ \ シ\ \ }}$
である。
ここで、$a=100$としたとき、無作為に抽出された留学生のうち、初級コースに
登録した留学生が28人以上となる確率を$p$とする。$a=100$は十分大きいので、
$Y$は近似的に正規分布に従う。このことを用いて$p$の近似値を求めると、
$p=\boxed{\boxed{\ \ ス\ \ }}$である。
$\boxed{\boxed{\ \ ス\ \ }}$については。最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪$0.002$ ①$0.023$ ②$0.228$ ③$0.477$ ④$0.480$ ⑤$0.977$
(2)40人の留学生を無作為に抽出し、ある1週間における留学生の日本語学習コース
以外の日本語の学習時間(分)を調査した。ただし、日本語の学習時間は母平均$m$,
母分散$\delta^2$の分布に従うものとする。
母分散$\delta^2$を$640$と仮定すると、標本平均の標準偏差は$\boxed{\ \ セ\ \ }$となる。
調査の結果、40人の学習時間の平均値は120であった。標本平均が近似的に
正規分布に従うとして、母平均$m$に対する信頼度95%の信頼区間を$C_1 \leqq m \leqq C_2$とすると
$C_1=\boxed{\ \ ソタチ\ \ }.\boxed{\ \ ツテ\ \ },$
$C_2=\boxed{\ \ トナニ\ \ }.\boxed{\ \ ヌネ\ \ }$
である。
(3)(2)の調査とは別に、日本語の学習時間を再度調査することになった。そこで、
50人の留学生を無作為に抽出し、調査した結果、学習時間の平均値は120であった。
母分散$\delta^2$を640と仮定したとき、母平均$m$に対する信頼度95%の信頼区間を
$D_1 \leqq m \leqq D_2$とすると、$\boxed{\boxed{\ \ ノ\ \ }}$が成り立つ。
一方、母分散$\delta^2$を960と仮定したとき、母平均$m$に対する信頼度95%の
信頼区間を$E_1 \leqq m \leqq E_2$とする。このとき、$D_2-D_1=E_2-E_1$と
なるためには、標本の大きさを50の$\boxed{\ \ ハ\ \ }.\boxed{\ \ ヒ\ \ }$倍にする必要がある。
$\boxed{\boxed{\ \ ノ\ \ }}$の解答群
⓪$D_1 \lt C_1$かつ$D_2 \lt C_2$ ①$D_1 \lt C_1$かつ$D_2 \gt C_2$
②$D_1 \gt C_1$かつ$D_2 \lt C_2$ ③$D_1 \gt C_1$かつ$D_2 \gt C_2$
2021共通テスト過去問
共通テスト2021年詳しい解説〜共通テスト2021年2B第3問〜統計

単元:
#数学(中学生)#大学入試過去問(数学)#確率分布と統計的な推測#確率分布#統計的な推測#センター試験・共通テスト関連#共通テスト#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\large第3問}$
Q高校の校長先生は、ある日、新聞で高校生の読書に関する記事を読んだ。そこで、
Q高校の生徒全員を対象に、直前の1週間の読書時間に関して、100人の
生徒を無作為に抽出して調査を行った。その結果、100人の生徒のうち、この
1週間に全く読書をしなかった生徒が36人であり、100人の生徒のこの1週間の
読書時間(分)の平均値は204であった。Q高校の生徒全員のこの1週間の読書時間
の母平均を$m$, 母標準偏差を150とする。
(1)全く読書をしなかった生徒の母比率を0.5とする。このとき、100人の無作為標本の
うちで全く読書をしなかった生徒の数を表す確率変数をXとすると、$X$は$\boxed{\boxed{\ \ ア\ \ }}$
に従う。また、Xの平均(期待値)は$\boxed{\ \ イウ\ \ }$、標準偏差は$\boxed{\ \ エ\ \ }$である。
$\boxed{\boxed{\ \ ア\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪正規分布$N(0,1)$
①二項分布$B(0,1)$
②正規分布$N(100,0.5)$
③二項分布$B(100,0.5)$
④正規分布$N(100,36)$
⑤二項分布$B(100,36)$
(2)標本の大きさ100は十分に大きいので、100人のうち全く読書をしなかった生徒
の数は近似的に正規分布に従う。
全く読書をしなかった生徒の母比率を0.5とするとき、全く読書をしなかった生徒
が36人以下となる確率を$p_5$とおく。$p_5$の近似値を求めると、$p_5=\boxed{\boxed{\ \ オ\ \ }}$である。
また、全く読書をしなかった生徒の母比率を0.4とするとき、全く読書をしなかった
生徒が36人以下となる確率を$p_4$とおくと、$\boxed{\boxed{\ \ カ\ \ }}$である。
$\boxed{\boxed{\ \ オ\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪$0.001$
①$0.003$
②$0.026$
③$0.050$
④$0.133$
⑤$0.497$
$\boxed{\boxed{\ \ カ\ \ }}$の解答群
⓪$p_4 \lt p_5$
①$p_4 = p_5$
②$p_4 \gt p_5$
(3)1週間の読書時間の母平均$m$に対する信頼度95%の信頼区間を
$C_1 \leqq m \leqq C_2$とする。標本の大きさ100は十分大きいことと、1週間
の読書時間の標本平均が204、母標準偏差が150であることを用いると、
$C_1+C_2=\boxed{\ \ キクケ\ \ }$、$C_2-C_1=\boxed{\ \ コサ\ \ }.\boxed{\ \ シ\ \ }$であることがわかる。
また、母平均$m$と$C_1,C_2$については$\boxed{\boxed{\ \ ス\ \ }}$。
$\boxed{\boxed{\ \ ス\ \ }}$の解答群
⓪$C_1 \leqq m \leqq C_2$が必ず成り立つ
①$m \leqq C_2$は必ず成り立つが、$C_1 \leqq m$が成り立つとは限らない
②$C_1 \leqq m$は必ず成り立つが、$m \leqq C_2$が成り立つとは限らない
③$C_1 \leqq m$も$m \leqq C_2$も成り立つとは限らない
(4)Q高校の図書委員長も、校長先生と同じ新聞記事を読んだため、校長先生が
調査をしていることを知らずに、図書委員会として校長先生と同様の調査を
独自に行った。ただし、調査期間は校長先生による調査と同じ直前の1週間であり、
対象をQ高校の生徒全員として100人の生徒を無作為に抽出した。その調査における
全く読書をしなかった生徒の数を$n$とする。
校長先生の調査結果によると全く読書をしなかった生徒は36人であり、
$\boxed{\boxed{\ \ セ\ \ }}$。
$\boxed{\boxed{\ \ セ\ \ }}$の解答群
⓪$n$は必ず36に等しい
①$n$は必ず36未満である
②$n$は必ず36より大きい
③$n$と36との大小はわからない
(5)(4)の図書委員会が行った調査結果による母平均$m$に対する信頼度95%の
信頼区間を$D_1 \leqq m \leqq D_2$、校長先生が行った調査結果による母平均$m$に対す
る信頼度95%の信頼区間を(3)の$C_1 \leqq m \leqq C_2$とする。ただし、母集団は同一
であり、1週間の読書時間の母標準偏差は150とする。
このとき、次の⓪~⑤のうち、正しいものは$\boxed{\boxed{\ \ ソ\ \ }}と\boxed{\boxed{\ \ タ\ \ }}$である。
$\boxed{\boxed{\ \ ソ\ \ }}$, $\boxed{\boxed{\ \ タ\ \ }}$の解答群(解答の順序は問わない。)
⓪$C_1=D_1とC_2=D_2$が必ず成り立つ。
①$C_1 \lt D_2$または$D_1 \lt C_2$のどちらか一方のみが成り立つ。
②$D_2 \lt C_1$または$C_2 \lt D_1$となる場合もある。
③$C_2-C_1 \gt D_2-D_1$が必ず成り立つ。
④$C_2-C_1 = D_2-D_1$が必ず成り立つ。
⑤$C_2-C_1 \lt D_2-D_1$が必ず成り立つ。
2021共通テスト過去問
この動画を見る
${\large第3問}$
Q高校の校長先生は、ある日、新聞で高校生の読書に関する記事を読んだ。そこで、
Q高校の生徒全員を対象に、直前の1週間の読書時間に関して、100人の
生徒を無作為に抽出して調査を行った。その結果、100人の生徒のうち、この
1週間に全く読書をしなかった生徒が36人であり、100人の生徒のこの1週間の
読書時間(分)の平均値は204であった。Q高校の生徒全員のこの1週間の読書時間
の母平均を$m$, 母標準偏差を150とする。
(1)全く読書をしなかった生徒の母比率を0.5とする。このとき、100人の無作為標本の
うちで全く読書をしなかった生徒の数を表す確率変数をXとすると、$X$は$\boxed{\boxed{\ \ ア\ \ }}$
に従う。また、Xの平均(期待値)は$\boxed{\ \ イウ\ \ }$、標準偏差は$\boxed{\ \ エ\ \ }$である。
$\boxed{\boxed{\ \ ア\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪正規分布$N(0,1)$
①二項分布$B(0,1)$
②正規分布$N(100,0.5)$
③二項分布$B(100,0.5)$
④正規分布$N(100,36)$
⑤二項分布$B(100,36)$
(2)標本の大きさ100は十分に大きいので、100人のうち全く読書をしなかった生徒
の数は近似的に正規分布に従う。
全く読書をしなかった生徒の母比率を0.5とするとき、全く読書をしなかった生徒
が36人以下となる確率を$p_5$とおく。$p_5$の近似値を求めると、$p_5=\boxed{\boxed{\ \ オ\ \ }}$である。
また、全く読書をしなかった生徒の母比率を0.4とするとき、全く読書をしなかった
生徒が36人以下となる確率を$p_4$とおくと、$\boxed{\boxed{\ \ カ\ \ }}$である。
$\boxed{\boxed{\ \ オ\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪$0.001$
①$0.003$
②$0.026$
③$0.050$
④$0.133$
⑤$0.497$
$\boxed{\boxed{\ \ カ\ \ }}$の解答群
⓪$p_4 \lt p_5$
①$p_4 = p_5$
②$p_4 \gt p_5$
(3)1週間の読書時間の母平均$m$に対する信頼度95%の信頼区間を
$C_1 \leqq m \leqq C_2$とする。標本の大きさ100は十分大きいことと、1週間
の読書時間の標本平均が204、母標準偏差が150であることを用いると、
$C_1+C_2=\boxed{\ \ キクケ\ \ }$、$C_2-C_1=\boxed{\ \ コサ\ \ }.\boxed{\ \ シ\ \ }$であることがわかる。
また、母平均$m$と$C_1,C_2$については$\boxed{\boxed{\ \ ス\ \ }}$。
$\boxed{\boxed{\ \ ス\ \ }}$の解答群
⓪$C_1 \leqq m \leqq C_2$が必ず成り立つ
①$m \leqq C_2$は必ず成り立つが、$C_1 \leqq m$が成り立つとは限らない
②$C_1 \leqq m$は必ず成り立つが、$m \leqq C_2$が成り立つとは限らない
③$C_1 \leqq m$も$m \leqq C_2$も成り立つとは限らない
(4)Q高校の図書委員長も、校長先生と同じ新聞記事を読んだため、校長先生が
調査をしていることを知らずに、図書委員会として校長先生と同様の調査を
独自に行った。ただし、調査期間は校長先生による調査と同じ直前の1週間であり、
対象をQ高校の生徒全員として100人の生徒を無作為に抽出した。その調査における
全く読書をしなかった生徒の数を$n$とする。
校長先生の調査結果によると全く読書をしなかった生徒は36人であり、
$\boxed{\boxed{\ \ セ\ \ }}$。
$\boxed{\boxed{\ \ セ\ \ }}$の解答群
⓪$n$は必ず36に等しい
①$n$は必ず36未満である
②$n$は必ず36より大きい
③$n$と36との大小はわからない
(5)(4)の図書委員会が行った調査結果による母平均$m$に対する信頼度95%の
信頼区間を$D_1 \leqq m \leqq D_2$、校長先生が行った調査結果による母平均$m$に対す
る信頼度95%の信頼区間を(3)の$C_1 \leqq m \leqq C_2$とする。ただし、母集団は同一
であり、1週間の読書時間の母標準偏差は150とする。
このとき、次の⓪~⑤のうち、正しいものは$\boxed{\boxed{\ \ ソ\ \ }}と\boxed{\boxed{\ \ タ\ \ }}$である。
$\boxed{\boxed{\ \ ソ\ \ }}$, $\boxed{\boxed{\ \ タ\ \ }}$の解答群(解答の順序は問わない。)
⓪$C_1=D_1とC_2=D_2$が必ず成り立つ。
①$C_1 \lt D_2$または$D_1 \lt C_2$のどちらか一方のみが成り立つ。
②$D_2 \lt C_1$または$C_2 \lt D_1$となる場合もある。
③$C_2-C_1 \gt D_2-D_1$が必ず成り立つ。
④$C_2-C_1 = D_2-D_1$が必ず成り立つ。
⑤$C_2-C_1 \lt D_2-D_1$が必ず成り立つ。
2021共通テスト過去問
2020年センター試験解説。福田の入試問題解説〜2020年センター試験IIB第5問〜確率分布と統計的な推測
単元:
#大学入試過去問(数学)#確率分布と統計的な推測#確率分布#統計的な推測#センター試験・共通テスト関連#センター試験#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\large第5問}$
ある市の市立図書館の利用状況について調査を行った。
(1)ある高校の生徒720人全員を対象に、ある1週間に市立図書館で借りた本の
冊数について調査を行った。
その結果、1冊も借りなかった生徒が612人、1冊借りた生徒が54人、
2冊借りた生徒が36人であり、3冊借りた生徒が18人であった。
4冊以上借りた生徒はいなかった。
この高校の生徒から1人を無作為に選んだ時、その生徒が借りた本の冊数
を表す確率変数を$X$とする。
このとき、$X$の平均(期待値)は$E(X)=\displaystyle \frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$であり、$X^2$の平均は
$E(X^2)=\displaystyle \frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$である。よって、$X$の標準偏差は
$\sigma(X)=\displaystyle \frac{\sqrt{\boxed{\ \ オ\ \ }}}{\boxed{\ \ カ\ \ }}\displaystyle$ である。
(2)市内の高校生全員を母集団とし、ある1週間に市立図書館を利用した生徒の
割合(母比率)を$p$とする。この母集団から600人を無作為に選んだ時、その
1週間に市立図書館を利用した生徒の数を確率変数$Y$で表す。
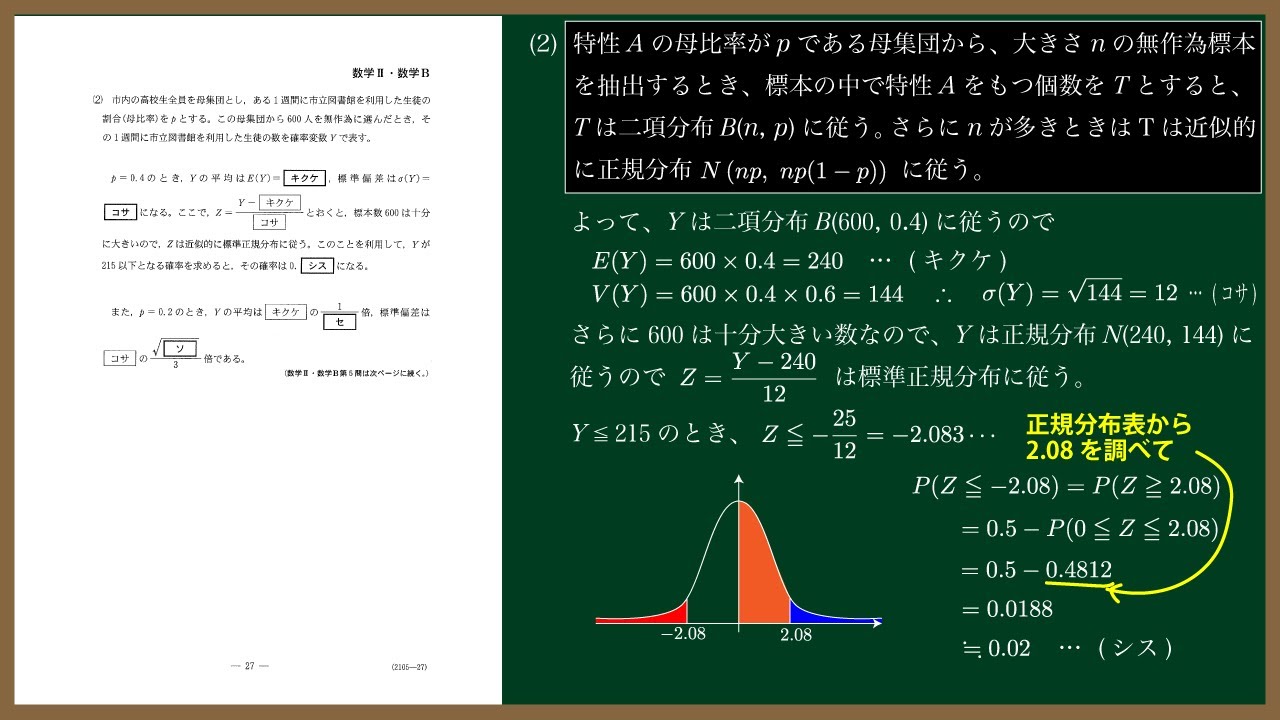
$p=0.4$のとき、$Y$の平均は$E(Y)=\boxed{\ \ キクケ\ \ }$、標準偏差は$\sigma(Y)=\boxed{\ \ コサ\ \ }$
になる。ここで、$Z=\displaystyle \frac{Y-\boxed{\ \ キクケ\ \ }}{\boxed{\ \ コサ\ \ }}\displaystyle$ とおくと、標本数600は
十分に大きいので、$Z$は近似的に標準正規分布に従う。このことを利用して、
$Y$が215以下となる確率を求めると、その確率は$0.\boxed{\ \ シス\ \ }$になる。
また、$p=0.2$のとき、$Y$の平均は$\boxed{\ \ キクケ\ \ }$の$\displaystyle \frac{1}{\boxed{\ \ セ\ \ }}$倍、
標準偏差は$\boxed{\ \ コサ\ \ }$の$\displaystyle \frac{\sqrt{\boxed{\ \ ソ\ \ }}}{3}$倍である。
(3)市立図書館に利用者登録のある高校生全員を母集団とする。1回あたりの
利用時間(分)を表す確率変数を$W$とし、$W$は母平均$m$,母標準偏差30の分布
に従うとする。この母集団から大きさ$n$の標本$W_1,W_2,\ldots,W_n$を無作為に
抽出した。
利用時間が60分をどの程度超えるかについて調査するために
$U_1=W_1-60, U_2=W_2-60, \ldots, U_n=W_n-60$
とおくと、確率変数$U_1,U_2, \cdots, U_n$の平均と標準偏差はそれぞれ
$E(U_1)=E(U_2)=\cdots=E(U_n)$$=m-\boxed{\ \ タチ\ \ }$
$\sigma(U_1)=\sigma(U_2)=\cdots=\sigma(U_n)$$=\boxed{\ \ ツテ\ \ }$
である。
ここで、$t=m-60$として、$t$に対する信頼度95%の信頼区間を求めよう。
この母集団から無作為抽出された100人の生徒に対して$U_1,U_2, \cdots,U_m$の
値を調べたところ、その標本平均の値が50分であった。標本数は十分大きい
ことを利用して、この信頼区間を求めると
$\boxed{\ \ トナ\ \ }.\boxed{\ \ ニ\ \ } \leqq t \leqq \boxed{\ \ ヌネ\ \ }.\boxed{\ \ ノ\ \ }$
になる。
2020センター試験過去問
この動画を見る
${\large第5問}$
ある市の市立図書館の利用状況について調査を行った。
(1)ある高校の生徒720人全員を対象に、ある1週間に市立図書館で借りた本の
冊数について調査を行った。
その結果、1冊も借りなかった生徒が612人、1冊借りた生徒が54人、
2冊借りた生徒が36人であり、3冊借りた生徒が18人であった。
4冊以上借りた生徒はいなかった。
この高校の生徒から1人を無作為に選んだ時、その生徒が借りた本の冊数
を表す確率変数を$X$とする。
このとき、$X$の平均(期待値)は$E(X)=\displaystyle \frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$であり、$X^2$の平均は
$E(X^2)=\displaystyle \frac{\boxed{\ \ ウ\ \ }}{\boxed{\ \ エ\ \ }}$である。よって、$X$の標準偏差は
$\sigma(X)=\displaystyle \frac{\sqrt{\boxed{\ \ オ\ \ }}}{\boxed{\ \ カ\ \ }}\displaystyle$ である。
(2)市内の高校生全員を母集団とし、ある1週間に市立図書館を利用した生徒の
割合(母比率)を$p$とする。この母集団から600人を無作為に選んだ時、その
1週間に市立図書館を利用した生徒の数を確率変数$Y$で表す。
$p=0.4$のとき、$Y$の平均は$E(Y)=\boxed{\ \ キクケ\ \ }$、標準偏差は$\sigma(Y)=\boxed{\ \ コサ\ \ }$
になる。ここで、$Z=\displaystyle \frac{Y-\boxed{\ \ キクケ\ \ }}{\boxed{\ \ コサ\ \ }}\displaystyle$ とおくと、標本数600は
十分に大きいので、$Z$は近似的に標準正規分布に従う。このことを利用して、
$Y$が215以下となる確率を求めると、その確率は$0.\boxed{\ \ シス\ \ }$になる。
また、$p=0.2$のとき、$Y$の平均は$\boxed{\ \ キクケ\ \ }$の$\displaystyle \frac{1}{\boxed{\ \ セ\ \ }}$倍、
標準偏差は$\boxed{\ \ コサ\ \ }$の$\displaystyle \frac{\sqrt{\boxed{\ \ ソ\ \ }}}{3}$倍である。
(3)市立図書館に利用者登録のある高校生全員を母集団とする。1回あたりの
利用時間(分)を表す確率変数を$W$とし、$W$は母平均$m$,母標準偏差30の分布
に従うとする。この母集団から大きさ$n$の標本$W_1,W_2,\ldots,W_n$を無作為に
抽出した。
利用時間が60分をどの程度超えるかについて調査するために
$U_1=W_1-60, U_2=W_2-60, \ldots, U_n=W_n-60$
とおくと、確率変数$U_1,U_2, \cdots, U_n$の平均と標準偏差はそれぞれ
$E(U_1)=E(U_2)=\cdots=E(U_n)$$=m-\boxed{\ \ タチ\ \ }$
$\sigma(U_1)=\sigma(U_2)=\cdots=\sigma(U_n)$$=\boxed{\ \ ツテ\ \ }$
である。
ここで、$t=m-60$として、$t$に対する信頼度95%の信頼区間を求めよう。
この母集団から無作為抽出された100人の生徒に対して$U_1,U_2, \cdots,U_m$の
値を調べたところ、その標本平均の値が50分であった。標本数は十分大きい
ことを利用して、この信頼区間を求めると
$\boxed{\ \ トナ\ \ }.\boxed{\ \ ニ\ \ } \leqq t \leqq \boxed{\ \ ヌネ\ \ }.\boxed{\ \ ノ\ \ }$
になる。
2020センター試験過去問
【高校数学】 数B-117(最終回) 推定

単元:
#確率分布と統計的な推測#確率分布#標本調査#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①大きさ100の標本の平均値は56.3で,標本標準偏差は10.2である.
このとき,母平均$m$に対して,信頼度95%の信頼区間を求めよう.
②ある工場で生産される製品の不良率を信頼度95%で推定したい.
この不良率がほぼ5%であると予想できるとき,
信頼区間の幅を0.02以下にするには標本の大きさをいくらにすればよいか求めよう.
この動画を見る
①大きさ100の標本の平均値は56.3で,標本標準偏差は10.2である.
このとき,母平均$m$に対して,信頼度95%の信頼区間を求めよう.
②ある工場で生産される製品の不良率を信頼度95%で推定したい.
この不良率がほぼ5%であると予想できるとき,
信頼区間の幅を0.02以下にするには標本の大きさをいくらにすればよいか求めよう.
【高校数学】 数B-116 母集団と標本②

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$P(1)=0.3413,P(2)=0.4772$として,次の確率を求めよう.
①母平均120,母標準偏差30をもつ母集団から,
大きさ100の無作為標本を抽出するとき,
その標本平均$\overline{X}$が123より大きい値をとる確率
②ある学校の生徒を母集団とするとき,
その身長は平均165cm,標準偏差4cmの正規分布をなしていた.
この母集団から無作為に64人の標本を抽出したとき,
その標本平均が164cm以上166cm以下である確率
この動画を見る
$P(1)=0.3413,P(2)=0.4772$として,次の確率を求めよう.
①母平均120,母標準偏差30をもつ母集団から,
大きさ100の無作為標本を抽出するとき,
その標本平均$\overline{X}$が123より大きい値をとる確率
②ある学校の生徒を母集団とするとき,
その身長は平均165cm,標準偏差4cmの正規分布をなしていた.
この母集団から無作為に64人の標本を抽出したとき,
その標本平均が164cm以上166cm以下である確率
【高校数学】 数B-115 母集団と標本①

単元:
#確率分布と統計的な推測#確率分布#標本調査#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
1,2,3の数字を記入した玉が,それぞれ2個,3個,5個袋の中に入っている.
これを母集団として,次の問いに答えよう.
①玉に書かれている数字の母集団分布を求めよう.
②母平均$m$,母分散$\sigma^2$,母標準偏差$\sigma$を求めよう。
この動画を見る
1,2,3の数字を記入した玉が,それぞれ2個,3個,5個袋の中に入っている.
これを母集団として,次の問いに答えよう.
①玉に書かれている数字の母集団分布を求めよう.
②母平均$m$,母分散$\sigma^2$,母標準偏差$\sigma$を求めよう。
【高校数学】 数B-114 正規分布③

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
確率変数$X$は正規分布$N(2,5^2)$に従うとき,
次の確率を求めよう.
ただし,$P(0.4)=0.1554,P(1)=0.3413,P(2)=0.4772$とする.
①$P(2\leqq X \leqq 12)$
②$P(0\leqq X \leqq 7)$
この動画を見る
確率変数$X$は正規分布$N(2,5^2)$に従うとき,
次の確率を求めよう.
ただし,$P(0.4)=0.1554,P(1)=0.3413,P(2)=0.4772$とする.
①$P(2\leqq X \leqq 12)$
②$P(0\leqq X \leqq 7)$
【高校数学】 数B-113 正規分布②

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
確率変数$Z$が標準正規分布$N(0,1)$に従うとき,
次の確率を求めよう.
ただし,$P(1)=0.3413,P(2)=0.4772$とする.
①$P(-1\leqq Z \leqq 2)$
②$P(1\leqq Z \leqq 2)$
③$P(Z\geqq 1)$
この動画を見る
確率変数$Z$が標準正規分布$N(0,1)$に従うとき,
次の確率を求めよう.
ただし,$P(1)=0.3413,P(2)=0.4772$とする.
①$P(-1\leqq Z \leqq 2)$
②$P(1\leqq Z \leqq 2)$
③$P(Z\geqq 1)$
【高校数学】 数B-112 正規分布①

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
確率変数$X$の確率密度関数$f(x)$が次の式で与えられたとき,
指定された確率をそれぞれ求めよう.
①$f(x)=2x(0\leqq x \leqq 1) \quad 0.3\leqq X \leqq 0.5$である確率
②$f(x)=1-\dfrac{1}{2}x(0\leqq x\leqq 2) \quad 0.4\leqq X \leqq 1.2$である確率
この動画を見る
確率変数$X$の確率密度関数$f(x)$が次の式で与えられたとき,
指定された確率をそれぞれ求めよう.
①$f(x)=2x(0\leqq x \leqq 1) \quad 0.3\leqq X \leqq 0.5$である確率
②$f(x)=1-\dfrac{1}{2}x(0\leqq x\leqq 2) \quad 0.4\leqq X \leqq 1.2$である確率
【高校数学】 数B-111 二項分布③

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①1個のさいころを100回投げて,3の倍数の目が出る回数をXとする.
$X$の期待値, 分散,標準偏差を求めよう.
②赤玉が6個,白玉が4個入った袋から1球を取り出し,色を調べてからもとに戻す.
これを6回繰り返して,赤玉の出た回数を$X$とするとき,
$X$の期待値,分散,標準偏差を求めよう.
この動画を見る
①1個のさいころを100回投げて,3の倍数の目が出る回数をXとする.
$X$の期待値, 分散,標準偏差を求めよう.
②赤玉が6個,白玉が4個入った袋から1球を取り出し,色を調べてからもとに戻す.
これを6回繰り返して,赤玉の出た回数を$X$とするとき,
$X$の期待値,分散,標準偏差を求めよう.
【高校数学】 数B-110 二項分布②

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の二項分布の平均,分散,標準偏差を求めよう.
①$B\left(9,\dfrac{2}{3}\right)$
②$B\left(5,\dfrac{1}{4}\right)$
この動画を見る
次の二項分布の平均,分散,標準偏差を求めよう.
①$B\left(9,\dfrac{2}{3}\right)$
②$B\left(5,\dfrac{1}{4}\right)$
【高校数学】 数B-109 二項分布①

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
1個のさいころを5回投げて,3の倍数の目が出る回数を$X$とする.
$X$はどのような二項分布に従うか.
また,次の確率を求めよう.
①$P(x=2)$
②$P(4\leqq X \leqq 5)$
③$P(X \leqq 2)$
この動画を見る
1個のさいころを5回投げて,3の倍数の目が出る回数を$X$とする.
$X$はどのような二項分布に従うか.
また,次の確率を求めよう.
①$P(x=2)$
②$P(4\leqq X \leqq 5)$
③$P(X \leqq 2)$
【高校数学】 数B-108 確率変数の和と積③

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
大中小3個のさいころを投げるとき,次の値を求めよう.
①出る目の和の期待値
②出る目の積の期待値
③出る目の和の分散
この動画を見る
大中小3個のさいころを投げるとき,次の値を求めよう.
①出る目の和の期待値
②出る目の積の期待値
③出る目の和の分散
【高校数学】 数B-107 確率変数の和と積②

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
袋Aには赤玉3個,白玉2個,袋Bには赤玉2個,白玉3個が入っている.
それぞれの袋から2個の玉を同時に取り出すとき,
取り出した計4個の中の白玉の個数を$X$とする.
①確率変数$X$の期待値を求めよう.
②確率変数$X$の分散を求めよう.
この動画を見る
袋Aには赤玉3個,白玉2個,袋Bには赤玉2個,白玉3個が入っている.
それぞれの袋から2個の玉を同時に取り出すとき,
取り出した計4個の中の白玉の個数を$X$とする.
①確率変数$X$の期待値を求めよう.
②確率変数$X$の分散を求めよう.
【高校数学】 数B-106 確率変数の和と積①

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①2枚の硬貨を同時に投げる試行を2回行う.
1回目の試行で表の出る枚数を$X$, 2回目の試行で表の出る枚数を$Y$とするとき,
$X$と$Y$の同時分布を求めよう.
この動画を見る
①2枚の硬貨を同時に投げる試行を2回行う.
1回目の試行で表の出る枚数を$X$, 2回目の試行で表の出る枚数を$Y$とするとき,
$X$と$Y$の同時分布を求めよう.
【高校数学】 数B-105 分散と標準偏差

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
確率変数$Y$の「確率分布が下の図で与えられるとき,
次の値を求めよう.
①$X$の分散
②$X$の標準偏差
$\begin{array}{c|ccc|c}
X & \ 0 & 1 & 2 & 計 \\
\hline
P & \dfrac{3}{6} & \dfrac{2}{6} & \dfrac{1}{6} & 1 & \\
\end{array}$
この動画を見る
確率変数$Y$の「確率分布が下の図で与えられるとき,
次の値を求めよう.
①$X$の分散
②$X$の標準偏差
$\begin{array}{c|ccc|c}
X & \ 0 & 1 & 2 & 計 \\
\hline
P & \dfrac{3}{6} & \dfrac{2}{6} & \dfrac{1}{6} & 1 & \\
\end{array}$
【高校数学】 数B-104 期待値②

単元:
#数A#場合の数と確率#確率#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①1個のさいころを投げ,「出た目の数×500円」を受け取るゲームをする.
1回さいころを投げるのに2000円かかるとき,
このゲームに参加するのは得か,損か.
②1個のさいころを5回投げて,「3の倍数の目が出る回数×100円」を受け取るゲームをする.
参加料が200円のとき,このゲームに参加することは得か,損か.
この動画を見る
①1個のさいころを投げ,「出た目の数×500円」を受け取るゲームをする.
1回さいころを投げるのに2000円かかるとき,
このゲームに参加するのは得か,損か.
②1個のさいころを5回投げて,「3の倍数の目が出る回数×100円」を受け取るゲームをする.
参加料が200円のとき,このゲームに参加することは得か,損か.
【高校数学】 数B-103 期待値①

単元:
#数A#場合の数と確率#確率#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の確率変数$X$の期待値を求めよう.
①白玉5個と黒玉3個が入った袋から3個の玉を同時に取り出すとき,
その中に含まれる黒玉の個数$X$
②1個のさいころを3回投げるとき,3の倍数の目が出た回数$X$
この動画を見る
次の確率変数$X$の期待値を求めよう.
①白玉5個と黒玉3個が入った袋から3個の玉を同時に取り出すとき,
その中に含まれる黒玉の個数$X$
②1個のさいころを3回投げるとき,3の倍数の目が出た回数$X$
【高校数学】 数B-102 確率分布と確率変数②

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①1個のさいころを3回投げるとき,出た目の最大値$X$の
確率分布を求めよう.
②白玉3個と黒玉4個が入った4個の玉を同時に取り出すとき,
その中に含まれる白玉の個数$Y$の確率分布を求めよう.
この動画を見る
①1個のさいころを3回投げるとき,出た目の最大値$X$の
確率分布を求めよう.
②白玉3個と黒玉4個が入った4個の玉を同時に取り出すとき,
その中に含まれる白玉の個数$Y$の確率分布を求めよう.
【高校数学】 数B-101 確率分布と確率変数①

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
問題1
2個のさいころを同時に投げて,出る目の差を$X$とする.
①$X$の確率分布を求めよう.
②確率$P(3\leqq X \leqq 4)$を求めよう.
問題2
3枚のコインを同時に投げるとき,表の出る枚数を$Y$とする.
③$Y$の確率分布を求めよう.
④確率$P(1\leqq Y \leqq 2)$を求めよう.
この動画を見る
問題1
2個のさいころを同時に投げて,出る目の差を$X$とする.
①$X$の確率分布を求めよう.
②確率$P(3\leqq X \leqq 4)$を求めよう.
問題2
3枚のコインを同時に投げるとき,表の出る枚数を$Y$とする.
③$Y$の確率分布を求めよう.
④確率$P(1\leqq Y \leqq 2)$を求めよう.
