 確率分布と統計的な推測
確率分布と統計的な推測
 確率分布と統計的な推測
確率分布と統計的な推測
確率分布と統計的推測 数B 推定1【ゆう☆たろうがていねいに解説】

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある町で、1つの政策に対する賛否を調べる世論調査を、任意に抽出した有権者400人に対して行ったところ、政策支持者は216人であった。この町の有権者1万人のうち、この政策の支持者は何人ぐらいいると推定されるか。95%の信頼度で推定せよ。
数千枚の答案の採点をした。信頼度95%、信頼区間の幅4点以下でその平均点を推定したいとすると、少なくとも何枚以上の答案を抜き出さなければならないか。また、信頼区間の幅2点以下で推定するとすればどうか。ただし、従来の経験で点数の標準偏差は15点としてよいことはわかっているものとする。
(1) 確率変数Zが標準正規分布に従うとき、P(|Z|≦◻︎)=0.99が成り立つ。◻︎に当てはまる最も適切な値を、次の①〜④のうちから1つ選べ。
①1.75 ②1.96 ③2.33 ④2.58
(2) ある試験を受けた高校生の中から、100人を任意に選んだところ、平均点は58.3点であった。母標準偏差を13.0点として、母平均を信頼度99%で推定せよ。
この動画を見る
ある町で、1つの政策に対する賛否を調べる世論調査を、任意に抽出した有権者400人に対して行ったところ、政策支持者は216人であった。この町の有権者1万人のうち、この政策の支持者は何人ぐらいいると推定されるか。95%の信頼度で推定せよ。
数千枚の答案の採点をした。信頼度95%、信頼区間の幅4点以下でその平均点を推定したいとすると、少なくとも何枚以上の答案を抜き出さなければならないか。また、信頼区間の幅2点以下で推定するとすればどうか。ただし、従来の経験で点数の標準偏差は15点としてよいことはわかっているものとする。
(1) 確率変数Zが標準正規分布に従うとき、P(|Z|≦◻︎)=0.99が成り立つ。◻︎に当てはまる最も適切な値を、次の①〜④のうちから1つ選べ。
①1.75 ②1.96 ③2.33 ④2.58
(2) ある試験を受けた高校生の中から、100人を任意に選んだところ、平均点は58.3点であった。母標準偏差を13.0点として、母平均を信頼度99%で推定せよ。
確率分布と統計的推測 数B 母集団分布【ゆう☆たろうがていねいに解説】

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
1,1,2,3,3の数字を記入した5枚のカードが袋の中にある。これを母集団とし、無作為に大きさ2の標本X1,X2を抽出する。
(1) 母集団分布と母平均を求めよ。
(2) 標本平均X(バー)の確率分布を、復元抽出、非復元抽出の各場合について求めよ。
1,2,3,4,5の数字を書いた5枚のカードが袋の中にある。これを母集団とし、書かれた数字が奇数であるという特性をAとするとき、次の問いに答えよ。
(1) 特性Aの母比率を求めよ。
(2) この母集団から、大きさ1の無作為標本を抽出するとき、特性Aの標本比率の確率分布を求めよ。
(3) この母集団から、大きさ2の無作為標本を抽出するとき、復元抽出、非復元抽出の各場合について、特性Aの標本比率の確率分布を求めよ。
1枚の硬貨をn回投げて、表の出る回数をXとするとき、|X/n-1/2|≦0.01となる確率が0.95以上になるためには、nをどのくらい大きくすればよいか。100未満を切り上げて答えよ。
この動画を見る
1,1,2,3,3の数字を記入した5枚のカードが袋の中にある。これを母集団とし、無作為に大きさ2の標本X1,X2を抽出する。
(1) 母集団分布と母平均を求めよ。
(2) 標本平均X(バー)の確率分布を、復元抽出、非復元抽出の各場合について求めよ。
1,2,3,4,5の数字を書いた5枚のカードが袋の中にある。これを母集団とし、書かれた数字が奇数であるという特性をAとするとき、次の問いに答えよ。
(1) 特性Aの母比率を求めよ。
(2) この母集団から、大きさ1の無作為標本を抽出するとき、特性Aの標本比率の確率分布を求めよ。
(3) この母集団から、大きさ2の無作為標本を抽出するとき、復元抽出、非復元抽出の各場合について、特性Aの標本比率の確率分布を求めよ。
1枚の硬貨をn回投げて、表の出る回数をXとするとき、|X/n-1/2|≦0.01となる確率が0.95以上になるためには、nをどのくらい大きくすればよいか。100未満を切り上げて答えよ。
確率分布と統計的推測 数B 二項分布【ユースケ・マセマティックがていねいに解説】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある植物の種子の発芽率は80%であるという。
この植物の種子を900個まいたとき、次の問いに答えよ。
(1) 750個以上の種子が発芽する確率を求めよ。
(2) 900 個のうちn個以上の種子が発芽する確率が 80%以上となるようなnの最大値を求めよ。
この動画を見る
ある植物の種子の発芽率は80%であるという。
この植物の種子を900個まいたとき、次の問いに答えよ。
(1) 750個以上の種子が発芽する確率を求めよ。
(2) 900 個のうちn個以上の種子が発芽する確率が 80%以上となるようなnの最大値を求めよ。
確率分布と統計的推測 数B 正規分布6【ユースケ・マセマティックがていねいに解説】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある2つの試験の結果は、平均点がそれぞれ57.6点、81.8点、標準偏差がそれぞれ10.3点、 5.7点であった。
Aは前者の試験を受けて75点、Bは後者の試験を受けて88点であった。
どちらの試験を受けても、受験者全体としては優劣がないものとすると、 AとBはどちらが優れていると考えられるか。
ただし、得点は正規分布に従うものとする。
この動画を見る
ある2つの試験の結果は、平均点がそれぞれ57.6点、81.8点、標準偏差がそれぞれ10.3点、 5.7点であった。
Aは前者の試験を受けて75点、Bは後者の試験を受けて88点であった。
どちらの試験を受けても、受験者全体としては優劣がないものとすると、 AとBはどちらが優れていると考えられるか。
ただし、得点は正規分布に従うものとする。
確率分布と統計的推測 数B 正規分布5【ユースケ・マセマティックがていねいに解説】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある試験での成績の結果は、平均71点,標準偏差8点であった。 得点の分布は正規分布に従うものとするとき、次の問いに答えよ。
(1)63点から87点のものが450人いた。受験者の総数は約何人か。
(2) (1) のとき、合格点を55点とすると、約何人が合格することになるか。
この動画を見る
ある試験での成績の結果は、平均71点,標準偏差8点であった。 得点の分布は正規分布に従うものとするとき、次の問いに答えよ。
(1)63点から87点のものが450人いた。受験者の総数は約何人か。
(2) (1) のとき、合格点を55点とすると、約何人が合格することになるか。
確率分布と統計的推測 数B 仮説検定【ゆう☆たろうがていねいに解説】

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
テニス選手A, Bの年間の対戦成績は、Aの23勝13敗であった。両選手の力に差があると判断してよいか。有意水準5%で検定せよ。
ある政党の5年前の支持率は20%であった。無作為に900人を選んで調査したところ、151人が支持しているという結果であった。支持率は5年前から下がったと判断してよいか。有意水準1%で検定せよ。
ある政党の5年前の支持率は20%であった。無作為に900人を選んで調査したところ、151人が支持しているという結果であった。支持率は5年前から下 がったと判断してよいか。有意水準1%で検定せよ。
この動画を見る
テニス選手A, Bの年間の対戦成績は、Aの23勝13敗であった。両選手の力に差があると判断してよいか。有意水準5%で検定せよ。
ある政党の5年前の支持率は20%であった。無作為に900人を選んで調査したところ、151人が支持しているという結果であった。支持率は5年前から下がったと判断してよいか。有意水準1%で検定せよ。
ある政党の5年前の支持率は20%であった。無作為に900人を選んで調査したところ、151人が支持しているという結果であった。支持率は5年前から下 がったと判断してよいか。有意水準1%で検定せよ。
確率分布と統計的推測 数B 正規分布4【ユースケ・マセマティックがていねいに解説】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
1000人の生徒に数学のテストをおこなったところ、その成績は平均48点、標準偏差15点であった。 成績が正規分布に従うものとするとき、次の問いに答えよ。
(1) ある生徒の得点が78点以上である確率はいくらか?
(2)78点以上の生徒は約何人いると考えられるか。
(3)30点以下の生徒は約何人いると考えられるか。
この動画を見る
1000人の生徒に数学のテストをおこなったところ、その成績は平均48点、標準偏差15点であった。 成績が正規分布に従うものとするとき、次の問いに答えよ。
(1) ある生徒の得点が78点以上である確率はいくらか?
(2)78点以上の生徒は約何人いると考えられるか。
(3)30点以下の生徒は約何人いると考えられるか。
確率分布と統計的推測 数B 正規分布3【ユースケ・マセマティックがていねいに解説】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある県における高校2年生の男子の身長が、平均170.0cm、標準偏差値5.2cmの正規分布に従うものとする。
(1) 身長が 165 cm 以上の生徒は、約何%いるか。整数値で答えよ
(2) 身長の高い方から10%の中に入るのは、何cm以上の生徒か。最も小さい整数値で答えよ。
この動画を見る
ある県における高校2年生の男子の身長が、平均170.0cm、標準偏差値5.2cmの正規分布に従うものとする。
(1) 身長が 165 cm 以上の生徒は、約何%いるか。整数値で答えよ
(2) 身長の高い方から10%の中に入るのは、何cm以上の生徒か。最も小さい整数値で答えよ。
確率分布と統計的推測 数B 正規分布2【ユースケ・マセマティックがていねいに解説】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
正規分布N(m. σ²) に従う確率変数Xについて、Xの取る値を
m-1.5σ, m-0.5σ, m+0.5σ, m+1.5σ
によって、5つの階級に分けると、 各階級に何%ずつ含まれるか。
この動画を見る
正規分布N(m. σ²) に従う確率変数Xについて、Xの取る値を
m-1.5σ, m-0.5σ, m+0.5σ, m+1.5σ
によって、5つの階級に分けると、 各階級に何%ずつ含まれるか。
確率分布と統計的推測 数B 正規分布1【ユースケ・マセマティックがていねいに解説】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
正規分布 N(10,5²)に従う確率変数Xについて、次の等式が成り立つように、
定数の値を定めよ。
(1) P(10≤ X ≤a)=0.4772
(2) P(X≥a)=0.0082
(3) P(|X-10|≤a)=0.8664
(4) P(|X-10|/≥a)=0.0278
正規分布N(m、σ²)において、変数Xが|X-m|≥kσの範囲に入る確率が、
次の値になるように、正の定数の値を定めよ。
(1) 0.006
(2) 0.016
(3) 0.242
この動画を見る
正規分布 N(10,5²)に従う確率変数Xについて、次の等式が成り立つように、
定数の値を定めよ。
(1) P(10≤ X ≤a)=0.4772
(2) P(X≥a)=0.0082
(3) P(|X-10|≤a)=0.8664
(4) P(|X-10|/≥a)=0.0278
正規分布N(m、σ²)において、変数Xが|X-m|≥kσの範囲に入る確率が、
次の値になるように、正の定数の値を定めよ。
(1) 0.006
(2) 0.016
(3) 0.242
確率分布と統計的推測 数B 確率密度関数【ユースケ・マセマティックがていねいに解説】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
確率変数Xのとる値の範囲が-1≤X≤1で、その確率密度関数(x)が f(x)=1-|x| (-1≤x≤1)で与えられるとき、次の確率を求めよ。
(1) P(0≤ X ≤0.25)
(2) P(|X| ≤0.25)
(3) P(-0.5≤ X ≤0.3)
確率変数Xのとる値の範囲が0≤x≤10で、その確率密度関数がkを定数として
f(x)=kx(10-x) (0≤x≤10)で与えられているとする。
このとき、kの値は□であり、確率 P(3≤x≤7) は□となる。
この動画を見る
確率変数Xのとる値の範囲が-1≤X≤1で、その確率密度関数(x)が f(x)=1-|x| (-1≤x≤1)で与えられるとき、次の確率を求めよ。
(1) P(0≤ X ≤0.25)
(2) P(|X| ≤0.25)
(3) P(-0.5≤ X ≤0.3)
確率変数Xのとる値の範囲が0≤x≤10で、その確率密度関数がkを定数として
f(x)=kx(10-x) (0≤x≤10)で与えられているとする。
このとき、kの値は□であり、確率 P(3≤x≤7) は□となる。
【高校数学】統計的な推測 2週間完成【⑦仮説検定】

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
・ある硬貨を484回投げたところ、おもてが222回出た。この硬貨は、表と裏の出方に偏りがあると判断してよいか。有意水準5%で検定せよ。
・あるテレビ番組の視聴率は従来10%であった。無作為に400世帯を選んで調査したところ、48世帯が視聴していることがわかった。視聴率は従来よりも上がったと判断してよいか。有意水準5%で検定せよ。
この動画を見る
・ある硬貨を484回投げたところ、おもてが222回出た。この硬貨は、表と裏の出方に偏りがあると判断してよいか。有意水準5%で検定せよ。
・あるテレビ番組の視聴率は従来10%であった。無作為に400世帯を選んで調査したところ、48世帯が視聴していることがわかった。視聴率は従来よりも上がったと判断してよいか。有意水準5%で検定せよ。
【高校数学】ここは大事!統計的な推測 2週間完成【⑥推定】

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
・ある試験を受けた高校生の中から、100人を任意に選んだところ、平均点は58.3点であった。母標準偏差を13.0点として、母平均を信頼度95%で推定せよ。
・ある町の有権者2500人を無作為に抽出して、A政党の支持者を調べたところ、625人であった。この町のA政党支持率を信頼度95%で推定せよ。
この動画を見る
・ある試験を受けた高校生の中から、100人を任意に選んだところ、平均点は58.3点であった。母標準偏差を13.0点として、母平均を信頼度95%で推定せよ。
・ある町の有権者2500人を無作為に抽出して、A政党の支持者を調べたところ、625人であった。この町のA政党支持率を信頼度95%で推定せよ。
【高校数学】模試までに整理すればまだ間に合う!統計的な推測 2週間完成【⑤母集団と標本】

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
・母平均120、母標準偏差30をもつ母集団から大きさ100の無作為標本を抽出するとき、その標本平均$\bar{X}$が123より大きい値をとる確率を求めよ。
・ある国の有権者の内閣支持率が50%であるとき、無作為に抽出した400人の有権者の内閣支持率をRとする。Rが48%以上、52%以下である確率を求めよ。
この動画を見る
・母平均120、母標準偏差30をもつ母集団から大きさ100の無作為標本を抽出するとき、その標本平均$\bar{X}$が123より大きい値をとる確率を求めよ。
・ある国の有権者の内閣支持率が50%であるとき、無作為に抽出した400人の有権者の内閣支持率をRとする。Rが48%以上、52%以下である確率を求めよ。
【高校数学】正規分布はこれ1本でマスター!統計的な推測 2週間完成【④正規分布】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
・1000人の生徒に数学のテストを行ったところ、その成績は平均48点、標準偏差15点であった。成績が正規分布に従うものとするとき、次の問いに答えよ。
(1) ある生徒の点数が78点以上である確率を求めよ。
(2) 78点以上の生徒は約何人いると考えられるか。
(3) 30点以下の生徒は約何人いると考えられるか。
・ある植物の種子の発芽率は80%であるという。この植物の種子を900個まいたとき、次の問いに答えよ。
(1) 750個以上の種子が発芽する確率を求めよ。
(2) 900個のうちn個以上の種子が発芽する確率が80%以上となるようなnの最大値を求めよ。
この動画を見る
・1000人の生徒に数学のテストを行ったところ、その成績は平均48点、標準偏差15点であった。成績が正規分布に従うものとするとき、次の問いに答えよ。
(1) ある生徒の点数が78点以上である確率を求めよ。
(2) 78点以上の生徒は約何人いると考えられるか。
(3) 30点以下の生徒は約何人いると考えられるか。
・ある植物の種子の発芽率は80%であるという。この植物の種子を900個まいたとき、次の問いに答えよ。
(1) 750個以上の種子が発芽する確率を求めよ。
(2) 900個のうちn個以上の種子が発芽する確率が80%以上となるようなnの最大値を求めよ。
【高校数学】模試に向けて今からでも間に合う!統計的な推測 2週間完成【③二項分布】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
・次の二項分布の平均、分散と標準偏差を求めよ。
$\displaystyle B(5,\frac{1}{6})$
・1個のさいころを8回投げるとき、4以上の目が出る回数をXとする。
(1) 4以上の目が3回以上出る確率を求めよ。
(2) 確率変数Xの期待値と標準偏差を求めよ。
この動画を見る
・次の二項分布の平均、分散と標準偏差を求めよ。
$\displaystyle B(5,\frac{1}{6})$
・1個のさいころを8回投げるとき、4以上の目が出る回数をXとする。
(1) 4以上の目が3回以上出る確率を求めよ。
(2) 確率変数Xの期待値と標準偏差を求めよ。
【高校数学】統計的な推測 2週間完成【②同時分布、確率変数の和の期待値、独立な確率変数】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
・500円硬貨2枚と100円硬貨1枚を同時に投げる。表の出た硬貨の金額の和の期待値を求めよ。
・Aは2枚、Bは3枚の硬貨を同時に投げ、表の出た枚数をそれぞれX,Yとするとき、積XYの期待値を求めよ。
この動画を見る
・500円硬貨2枚と100円硬貨1枚を同時に投げる。表の出た硬貨の金額の和の期待値を求めよ。
・Aは2枚、Bは3枚の硬貨を同時に投げ、表の出た枚数をそれぞれX,Yとするとき、積XYの期待値を求めよ。
【高校数学】模試に向けて今からでも間に合う!統計的な推測 2週間完成【①確率変数と確率分布、期待値、分散、標準偏差、確率変数の変換】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
・3枚の硬貨を同時に投げるとき、表の出る枚数をXとする。確率変数Xの確率分布を求めよ。
・1個のサイコロを1回投げるとき、出る目の数をXとする。Xの期待値、分散、標準偏差を求めよ。
この動画を見る
・3枚の硬貨を同時に投げるとき、表の出る枚数をXとする。確率変数Xの確率分布を求めよ。
・1個のサイコロを1回投げるとき、出る目の数をXとする。Xの期待値、分散、標準偏差を求めよ。
【FULL】定期テスト直前対策!確率、確率分布と統計的な推測解説動画フルパック流し【数A,数B】

単元:
#数A#場合の数と確率#確率#確率分布と統計的な推測#確率分布#統計的な推測#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
確率、確率分布と統計的な推測のまとめ動画です。
確率の基本から信頼度区間の問題まで
見たい内容のシーンをチャプターから選んで下さい!!
この動画を見る
確率、確率分布と統計的な推測のまとめ動画です。
確率の基本から信頼度区間の問題まで
見たい内容のシーンをチャプターから選んで下さい!!
確率分布と統計的推測 数B 確率分布の問題3【ユースケ・マセマティックがていねいに解説】
単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
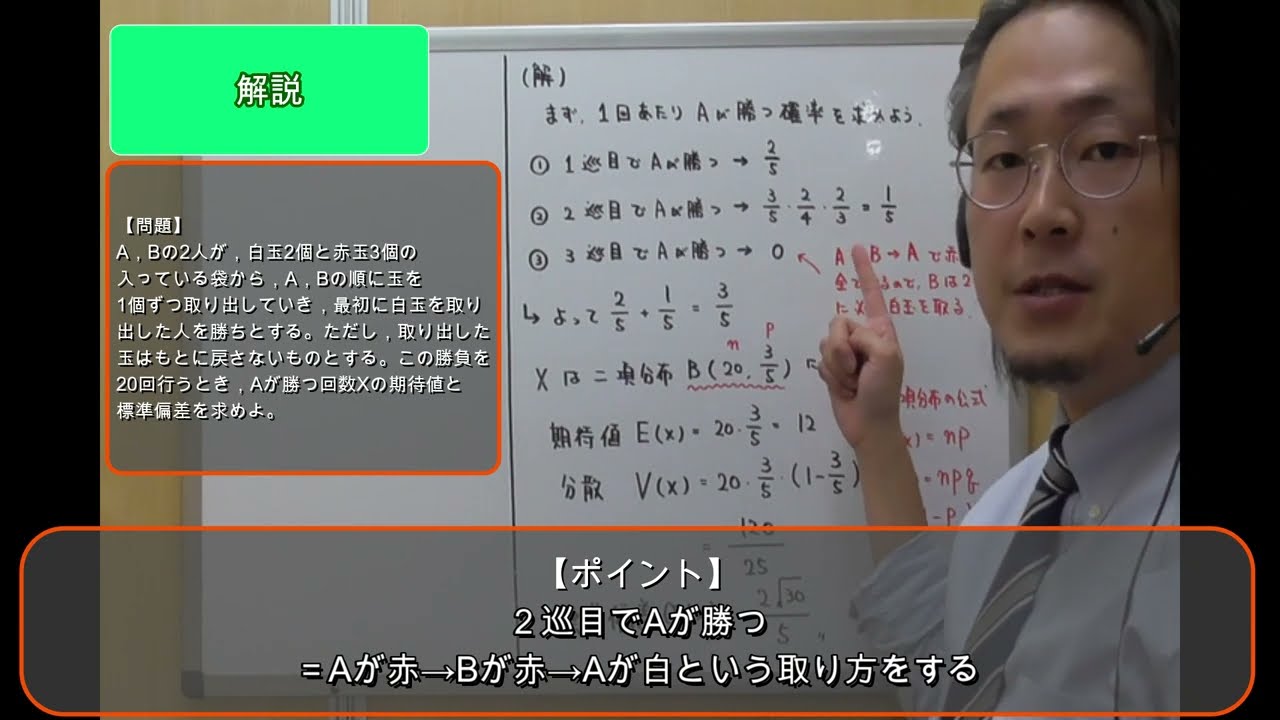
【問題】
A,Bの2人が,白玉2個と赤玉3個の入っている袋から,A,Bの順に玉を1個ずつ取り出していき,最初に白玉を取り出した人を勝ちとする。ただし,取り出した玉はもとに戻さないものとする。この勝負を20回行うとき,Aが勝つ回数Xの期待値と標準偏差を求めよ。
この動画を見る
【問題】
A,Bの2人が,白玉2個と赤玉3個の入っている袋から,A,Bの順に玉を1個ずつ取り出していき,最初に白玉を取り出した人を勝ちとする。ただし,取り出した玉はもとに戻さないものとする。この勝負を20回行うとき,Aが勝つ回数Xの期待値と標準偏差を求めよ。
確率分布と統計的推測 数B 確率分布の問題2【ユースケ・マセマティックがていねいに解説】
単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
【問題1】
2つの事象A,Bが独立であって,$P(A)=\frac{1}{2}$,$P(B)=\frac{1}{3}$であるとき,次の問いに答えよ。
(1)A,Bのうち少なくとも一方が起こる確率を求めよ。
(2) A,Bのうちどちらか一方のみが起こる確率を求めよ。
【問題2】
2,4,6の目が2面ずつ書かれた3個のさいころを同時に投げるとき,出る目の積の期待値を求めよ。
【問題3】
1つの面には1,2つの面には2,3つの面には3が書かれているさいころを2回投げて,1回目に出た目の数を十の位,2回目に出た目の数を一の位として得られる2桁の数をXとする。
(1)Xの確率分布を求めよ。
(2)Xの期待値と分散を求めよ。
この動画を見る
【問題1】
2つの事象A,Bが独立であって,$P(A)=\frac{1}{2}$,$P(B)=\frac{1}{3}$であるとき,次の問いに答えよ。
(1)A,Bのうち少なくとも一方が起こる確率を求めよ。
(2) A,Bのうちどちらか一方のみが起こる確率を求めよ。
【問題2】
2,4,6の目が2面ずつ書かれた3個のさいころを同時に投げるとき,出る目の積の期待値を求めよ。
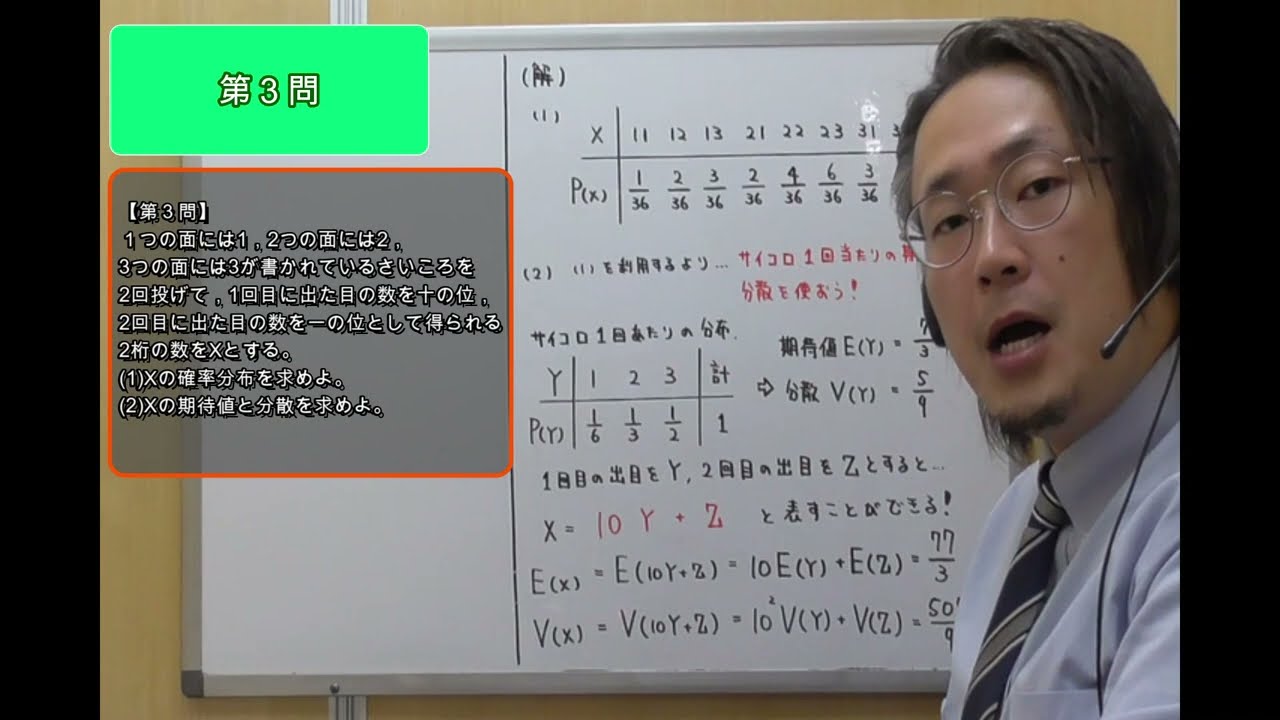
【問題3】
1つの面には1,2つの面には2,3つの面には3が書かれているさいころを2回投げて,1回目に出た目の数を十の位,2回目に出た目の数を一の位として得られる2桁の数をXとする。
(1)Xの確率分布を求めよ。
(2)Xの期待値と分散を求めよ。
確率分布と統計的推測 数B 確率分布の問題1【ユースケ・マセマティックがていねいに解説】
単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
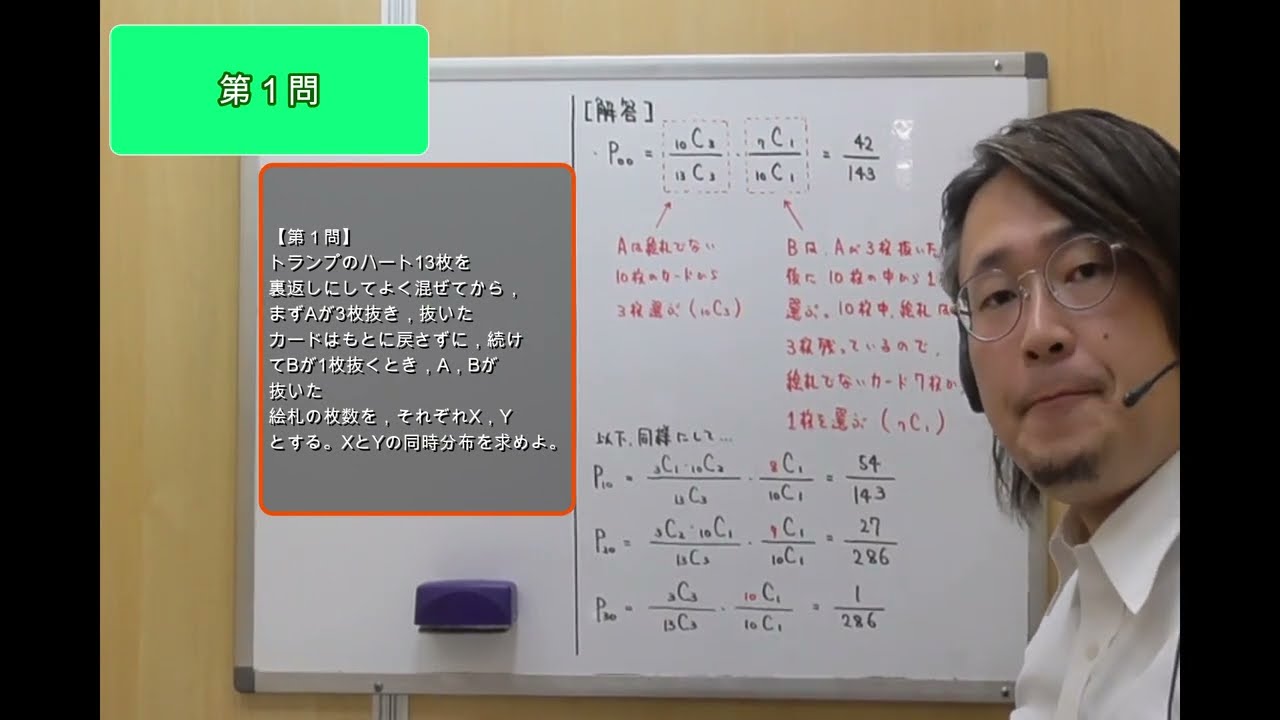
第1問
トランプのハート13枚を裏返しにしてよく混ぜてから,まずAが3枚抜き,抜いたカードはもとに戻さずに,続けてBが1枚抜くとき,A,Bが抜いた絵札の枚数を,それぞれX,Yとする。XとYの同時分布を求めよ。
第2問
100本のくじの中に30本の当たりくじがある。このくじから10本のくじを続けて引くとき,その中の当たりくじの本数をYとする。確率変数Yの期待値を求めよ。ただし,引いたくじはもとに戻さないとする。
この動画を見る
第1問
トランプのハート13枚を裏返しにしてよく混ぜてから,まずAが3枚抜き,抜いたカードはもとに戻さずに,続けてBが1枚抜くとき,A,Bが抜いた絵札の枚数を,それぞれX,Yとする。XとYの同時分布を求めよ。
第2問
100本のくじの中に30本の当たりくじがある。このくじから10本のくじを続けて引くとき,その中の当たりくじの本数をYとする。確率変数Yの期待値を求めよ。ただし,引いたくじはもとに戻さないとする。
確率分布と統計的推測 数B 確率変数の期待値と分散4【ユースケ・マセマティックがていねいに解説】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
Nは2以上の自然数とする。1からnまでの自然数1, 2,………, nの各数を1つずつ書いたn枚のカードが入った箱がある。この箱から同時に2枚のカードを取り出して,そのうち大きい方の数をXとする。
(1)1≦k≦nである自然数kに対してX=kとなる確率を求めよ。
(2)Xの期待値と分散を求めよ。
この動画を見る
Nは2以上の自然数とする。1からnまでの自然数1, 2,………, nの各数を1つずつ書いたn枚のカードが入った箱がある。この箱から同時に2枚のカードを取り出して,そのうち大きい方の数をXとする。
(1)1≦k≦nである自然数kに対してX=kとなる確率を求めよ。
(2)Xの期待値と分散を求めよ。
確率分布と統計的推測 数B 確率変数の期待値と分散3【ユースケ・マセマティックがていねいに解説】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
1と書かれたカードが2枚,2と書かれたカードが2枚,4と書かれたカードが1枚,計5枚のカードがある。この中から2枚のカードを取り出し,それらに書かれている数の和をXとするとき,確率変数Xの期待値と分散を求めよ。
この動画を見る
1と書かれたカードが2枚,2と書かれたカードが2枚,4と書かれたカードが1枚,計5枚のカードがある。この中から2枚のカードを取り出し,それらに書かれている数の和をXとするとき,確率変数Xの期待値と分散を求めよ。
確率分布と統計的推測 数B 確率変数の期待値と分散2【ユースケ・マセマティックがていねいに解説】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
白玉6個と赤玉4個が入っている袋から玉を次の方法で取り出す。白玉の出た回数をXとするとき,Xの期待値と分散をそれぞれ求めよ。
(1)1個ずつ,もとに戻さず2回続けて取り出す。
(2)1個ずつ,2回取り出す。ただし,取り出した玉は毎回もとに戻す。
この動画を見る
白玉6個と赤玉4個が入っている袋から玉を次の方法で取り出す。白玉の出た回数をXとするとき,Xの期待値と分散をそれぞれ求めよ。
(1)1個ずつ,もとに戻さず2回続けて取り出す。
(2)1個ずつ,2回取り出す。ただし,取り出した玉は毎回もとに戻す。
確率分布と統計的推測 数B 確率変数の期待値と分散1【ユースケ・マセマティックがていねいに解説】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある確率変数Xの確率分布が下の表で与えられている。Xの期待値が3.2であるとき,p, qの値を求めよ。
X 1 2 3 4 5
P p q p p q
この動画を見る
ある確率変数Xの確率分布が下の表で与えられている。Xの期待値が3.2であるとき,p, qの値を求めよ。
X 1 2 3 4 5
P p q p p q
確率分布と統計的推測 数B 確率変数と確率分布【ユースケ・マセマティックがていねいに解説】

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
【問題1】
4枚の硬貨を同時に投げる試行を4回繰り返すとき,2枚が表で2枚が裏となる回数をXとする。P(X=k)(k=0,1,2,3,4)の式を求めよ。
【問題2】
4つの箱があり、その箱に,それぞれ1,2,3,4の番号がつけられている。1,2,3,4の番号がつけられている4枚のカードを1つの箱に1枚ずつ入れるとき,カードの番号と箱の番号が一致したものの個数をXとする。このとき,Xの確率分布と,P(X>2), P(X≦2)を求めよ。
この動画を見る
【問題1】
4枚の硬貨を同時に投げる試行を4回繰り返すとき,2枚が表で2枚が裏となる回数をXとする。P(X=k)(k=0,1,2,3,4)の式を求めよ。
【問題2】
4つの箱があり、その箱に,それぞれ1,2,3,4の番号がつけられている。1,2,3,4の番号がつけられている4枚のカードを1つの箱に1枚ずつ入れるとき,カードの番号と箱の番号が一致したものの個数をXとする。このとき,Xの確率分布と,P(X>2), P(X≦2)を求めよ。
仮説検定を分かりやすく!頻度確率を用いて計算しよう!

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ダーツの矢を投げて、統計を取ると20に入る頻度が1000回中800回のプレイヤーが、10回投げたところ9回、20に入った。このプレイヤーは調子が良いか?
この動画を見る
ダーツの矢を投げて、統計を取ると20に入る頻度が1000回中800回のプレイヤーが、10回投げたところ9回、20に入った。このプレイヤーは調子が良いか?
仮説検定を分かりやすく!概念から計算まで

はじめしゃちょーの宝くじ710万円購入210万円当選を数学的に考える

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
はじめしゃちょーの宝くじ710万円購入210万円当選を数学的に考えていきます.
この動画を見る
はじめしゃちょーの宝くじ710万円購入210万円当選を数学的に考えていきます.
