 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
【数Ⅲ】極限:次の無限級数の和を求めよう。Σ[n=1~∞](-1/3)^n sin(nπ/2)

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の無限級数の和を求めよう。
$\displaystyle \sum_{n=1}^{\infty}\left(-\dfrac{1}{3}\right)^n \sin\dfrac{n\pi}{2}$
この動画を見る
次の無限級数の和を求めよう。
$\displaystyle \sum_{n=1}^{\infty}\left(-\dfrac{1}{3}\right)^n \sin\dfrac{n\pi}{2}$
【数Ⅲ】極限:次の無限級数の和を求めよう。Σ[n=1~∞](1/3)^n cosnπ

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の無限級数の和を求めよう。
$\displaystyle \sum_{n=1}^{\infty}\left(\dfrac{1}{3}\right)^n \cos n\pi$
この動画を見る
次の無限級数の和を求めよう。
$\displaystyle \sum_{n=1}^{\infty}\left(\dfrac{1}{3}\right)^n \cos n\pi$
07愛知県教員採用試験(数学:7番 複素数)

単元:
#数Ⅱ#複素数と方程式#複素数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{7}$ $\vert Z \vert=1,Z^5=1$
$Z\leftarrow \in $を求めよ.
この動画を見る
$\boxed{7}$ $\vert Z \vert=1,Z^5=1$
$Z\leftarrow \in $を求めよ.
ガウス記号・漸化式・合同式

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$[(7+\sqrt{41}^{2021}]$を$2^{2021}$で割った余りを求めよ.
この動画を見る
$[(7+\sqrt{41}^{2021}]$を$2^{2021}$で割った余りを求めよ.
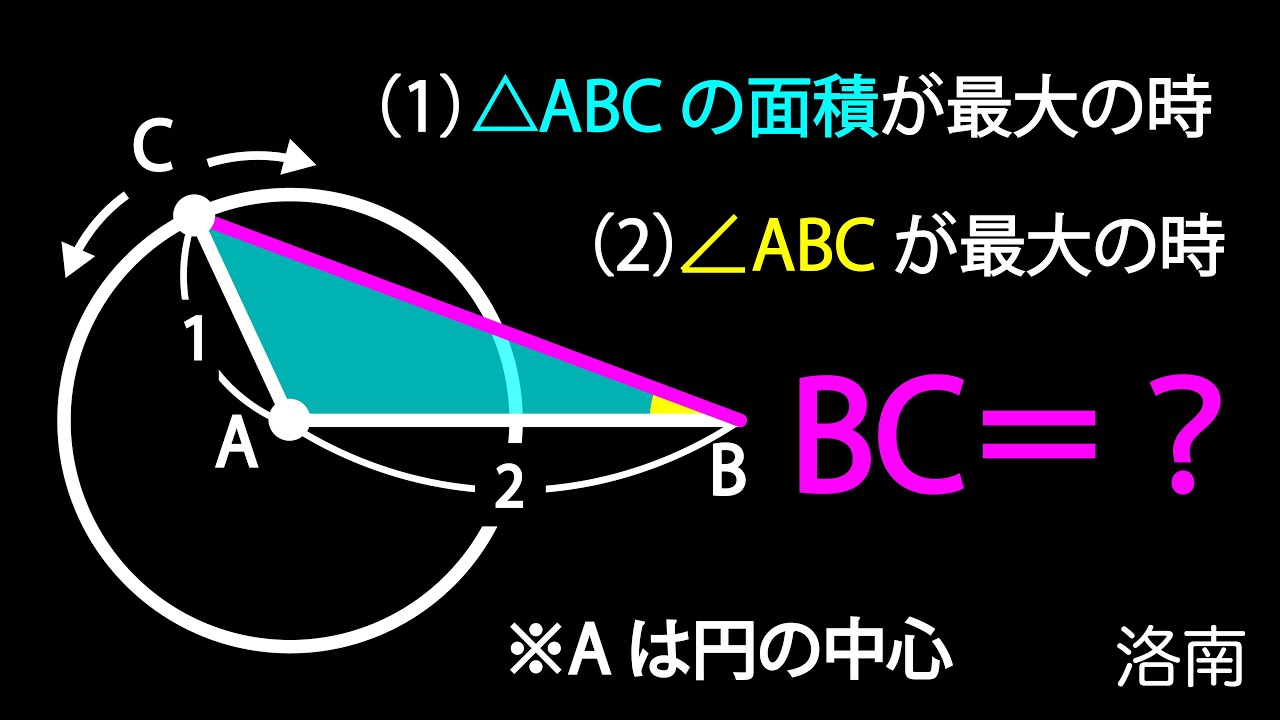
円 面積最大 角度最大 A
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
(1)△ABCの面積が最大の時
(2)$\angle ABC$が最大の時
BC=?
*図は動画内参照
洛南高等学校
この動画を見る
(1)△ABCの面積が最大の時
(2)$\angle ABC$が最大の時
BC=?
*図は動画内参照
洛南高等学校
特殊なBBB部分分数分解

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\dfrac{1^2}{1・3}+\dfrac{2^2}{3・5}+\dfrac{3^2}{5・7}+・・・・+\dfrac{50^2}{99・101}$
この動画を見る
これを解け.
$\dfrac{1^2}{1・3}+\dfrac{2^2}{3・5}+\dfrac{3^2}{5・7}+・・・・+\dfrac{50^2}{99・101}$
04愛知県教員採用試験(数学:10番 重積分)

単元:
#積分とその応用#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\iint_D f \ x \ dx\ dy$
$ D:\sqrt{\dfrac{x}{4}}+\sqrt{\dfrac{y}{3}}\leqq 1 $
これを解け.
図は動画内参照
この動画を見る
$\iint_D f \ x \ dx\ dy$
$ D:\sqrt{\dfrac{x}{4}}+\sqrt{\dfrac{y}{3}}\leqq 1 $
これを解け.
図は動画内参照
04愛知県教員採用試験(数学:14番 楕円、接線、相加相乗平均)

単元:
#微分とその応用#接線と法線・平均値の定理#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{14}$ $a\gt 0,b\gt 0$
楕円$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$
の接線がx軸,y軸と交わる点を$P.Q$とする.
$PQ$の最小値を求めよ.
この動画を見る
$\boxed{14}$ $a\gt 0,b\gt 0$
楕円$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$
の接線がx軸,y軸と交わる点を$P.Q$とする.
$PQ$の最小値を求めよ.
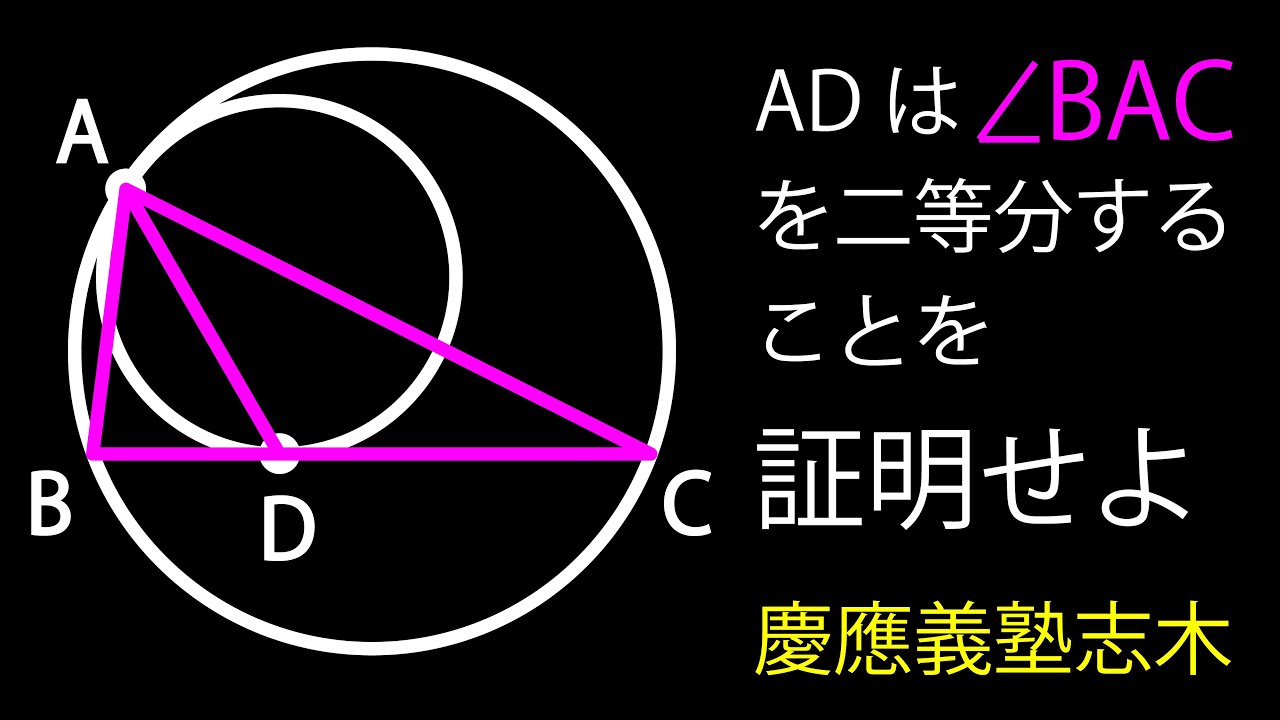
二つの円 角の二等分線 C
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
ADは$\angle BAC$を二等分することを示せ
*図は動画内参照
慶應義塾志木高等学校
この動画を見る
ADは$\angle BAC$を二等分することを示せ
*図は動画内参照
慶應義塾志木高等学校
【高校数学】互いに素~基本事項と使い方~ 5-4 【数学A】

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
nは整数とする。
n,n+1は互いに素であることを示せ
この動画を見る
nは整数とする。
n,n+1は互いに素であることを示せ
【共テ】数学IIB 第5問_直前のベクトル攻略法【空間ベクトル】

バーゼル問題 出題されてから91年後にオイラーが解決

単元:
#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$n\to \infty$とする.
$\dfrac{1}{1^2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+・・・・+\dfrac{1}{n^2}=\dfrac{\boxed{?}}{6}$
この動画を見る
これを解け.$n\to \infty$とする.
$\dfrac{1}{1^2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+・・・・+\dfrac{1}{n^2}=\dfrac{\boxed{?}}{6}$
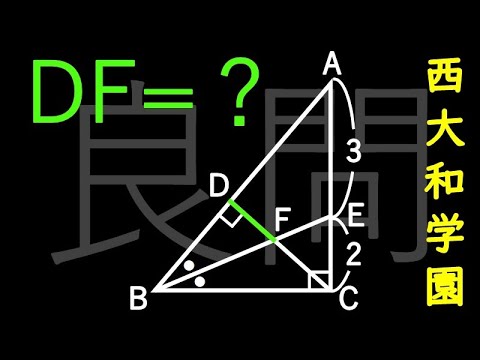
三平方の定理不要! 西大和学園 B
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
DF=?
*図は動画内参照
西大和学園高等学校
この動画を見る
DF=?
*図は動画内参照
西大和学園高等学校
「正弦定理・余弦定理・面積公式」【高校数学ⅠA】を宇宙一わかりやすく

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
正弦定理・余弦定理・面積公式の解説動画です
この動画を見る
正弦定理・余弦定理・面積公式の解説動画です
【数Ⅱ】複素数と方程式:2x²-6x-3=0の解がα、βのとき、①β²/α+α²/β②(2α²-6α-5)(2β²-6β-1)の値を求めよ。

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$2x^2-6x-3=0$の解が$\alpha,\beta$のとき、
①$\dfrac{\beta^2}{\alpha}+\dfrac{\alpha^2}{\beta}
②$(2\alpha^2-6\alpha-5)(2\beta^2-6\beta-1)$の値を求めよ。
この動画を見る
$2x^2-6x-3=0$の解が$\alpha,\beta$のとき、
①$\dfrac{\beta^2}{\alpha}+\dfrac{\alpha^2}{\beta}
②$(2\alpha^2-6\alpha-5)(2\beta^2-6\beta-1)$の値を求めよ。
微分方程式⑨【連立微分方程式】(高専数学、数検1級)

単元:
#数学検定・数学甲子園・数学オリンピック等#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{dx}{dt}=4y-\cos t \\
\dfrac{dy}{dt}=-x+\sin t
\end{array}
\right.
\end{eqnarray}$
これを解け.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{dx}{dt}=4y-\cos t \\
\dfrac{dy}{dt}=-x+\sin t
\end{array}
\right.
\end{eqnarray}$
これを解け.
sin10 vs sin11(弧度法)どっちがでかい?

単元:
#数Ⅱ#三角関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?$3\lt \pi \lt 4$である.
$\sin 10$ VS $\sin 11$
この動画を見る
どちらが大きいか?$3\lt \pi \lt 4$である.
$\sin 10$ VS $\sin 11$
平方根の計算 A コメント欄に良い解説あり!

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\frac{1}{\sqrt 2} - \frac{1}{\sqrt 3})(\frac{1}{\sqrt 6} + \frac{1}{3})=$
日比谷高等学校
この動画を見る
$(\frac{1}{\sqrt 2} - \frac{1}{\sqrt 3})(\frac{1}{\sqrt 6} + \frac{1}{3})=$
日比谷高等学校
【共通テスト】数学IIB第4問_数列 25分で安定させる!!

07神奈川県教員採用試験(数学:9番 領域と最小値)

単元:
#数Ⅱ#図形と方程式#微分法と積分法#軌跡と領域#接線と増減表・最大値・最小値#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{9}$
$x^2+xy-2y^2+6y-4\geqq 0$
$x^2+y^2$の最小値を求めよ.
この動画を見る
$\boxed{9}$
$x^2+xy-2y^2+6y-4\geqq 0$
$x^2+y^2$の最小値を求めよ.
剰余

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$111^{2021}$を$1111$で割った余りを求めよ.
この動画を見る
$111^{2021}$を$1111$で割った余りを求めよ.
整数問題 京都女子
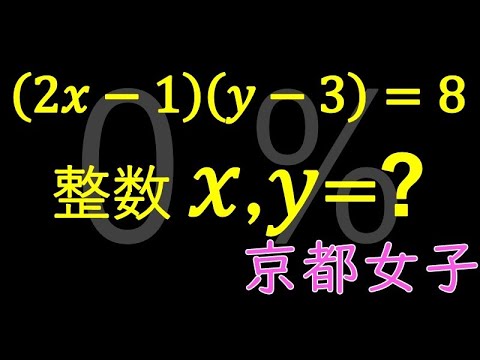
単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(2x-1)(y-3) =8$となる整数x、yの値を求めよ。
京都女子高等学校
この動画を見る
$(2x-1)(y-3) =8$となる整数x、yの値を求めよ。
京都女子高等学校
練習問題9(数検準1級 教員採用試験 極限値からの区分求積法)【難】
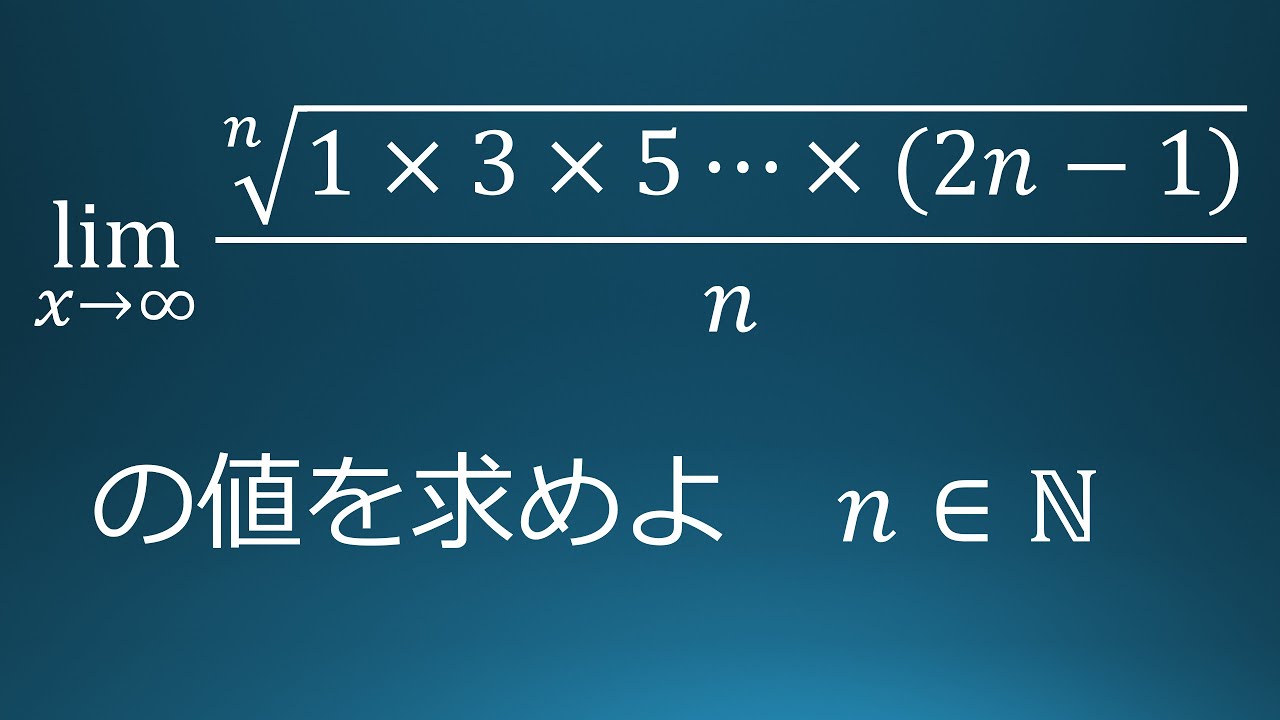
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#その他#数学検定#数学検定準1級#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
限値からの区分求積法を解説していきます.
この動画を見る
限値からの区分求積法を解説していきます.
数理クイズ

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
数理クイズ.これを解け.
$5\times 5=23$
$6\times 6=33$
$7\times 7=45$
$8\times 8=59$
$ 9\times 9=?$
$ 10\times 10=100$
この動画を見る
数理クイズ.これを解け.
$5\times 5=23$
$6\times 6=33$
$7\times 7=45$
$8\times 8=59$
$ 9\times 9=?$
$ 10\times 10=100$
良問!広島県!
練習問題8(数検準1級 教員採用試験 極限値からの区分求積法)
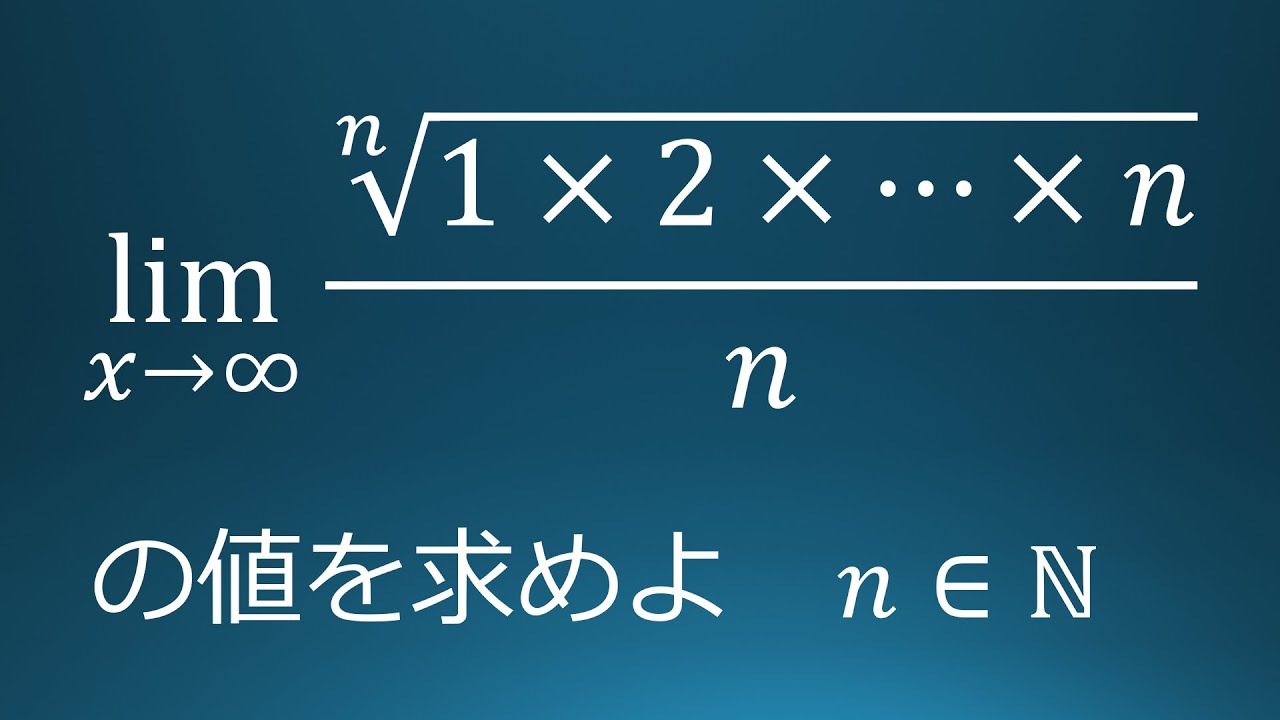
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#その他#数学検定#数学検定準1級#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{n\to\infty} \dfrac{\sqrt[n]{1\times 3\times 5\times ・・・ \times(2n-1)}}{n}$
これを解け.
この動画を見る
$\displaystyle \lim_{n\to\infty} \dfrac{\sqrt[n]{1\times 3\times 5\times ・・・ \times(2n-1)}}{n}$
これを解け.
n人でジャンケン あいこの確率

練習問題7(数検準1級 教員採用試験 極限値)
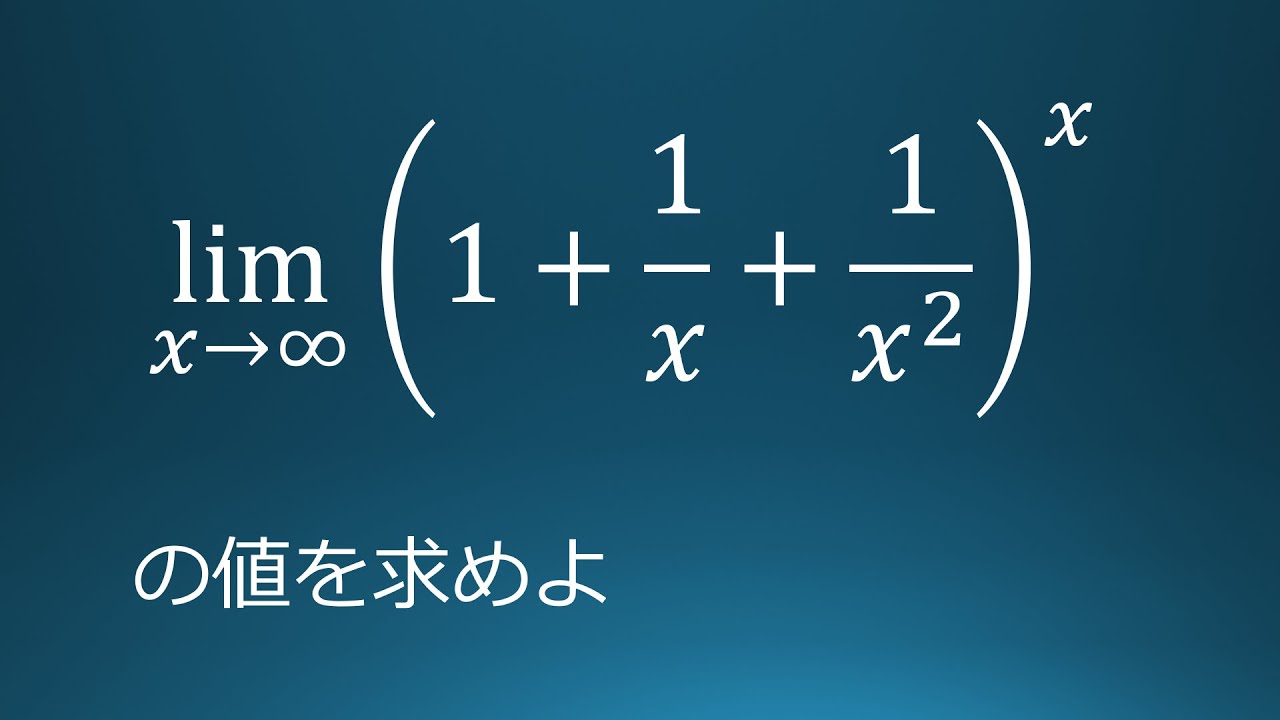
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#その他#数学検定#数学検定準1級#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{x\to\infty} \left(1+\dfrac{1}{x}+\dfrac{1}{x^2}\right)^x$
これを解け.
この動画を見る
$\displaystyle \lim_{x\to\infty} \left(1+\dfrac{1}{x}+\dfrac{1}{x^2}\right)^x$
これを解け.
ネイピア数の分数式がスッキリきれいな数字に

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\dfrac{e}{\sqrt e}・\dfrac{\sqrt[3]{e}}{\sqrt[4]{e}}・\dfrac{\sqrt[5]{e}}{\sqrt[6]{e}}・・・・・・=?$
この動画を見る
これを解け.
$\dfrac{e}{\sqrt e}・\dfrac{\sqrt[3]{e}}{\sqrt[4]{e}}・\dfrac{\sqrt[5]{e}}{\sqrt[6]{e}}・・・・・・=?$
練習問題6(数検準1級 教員採用試験 極限値【やや難】)
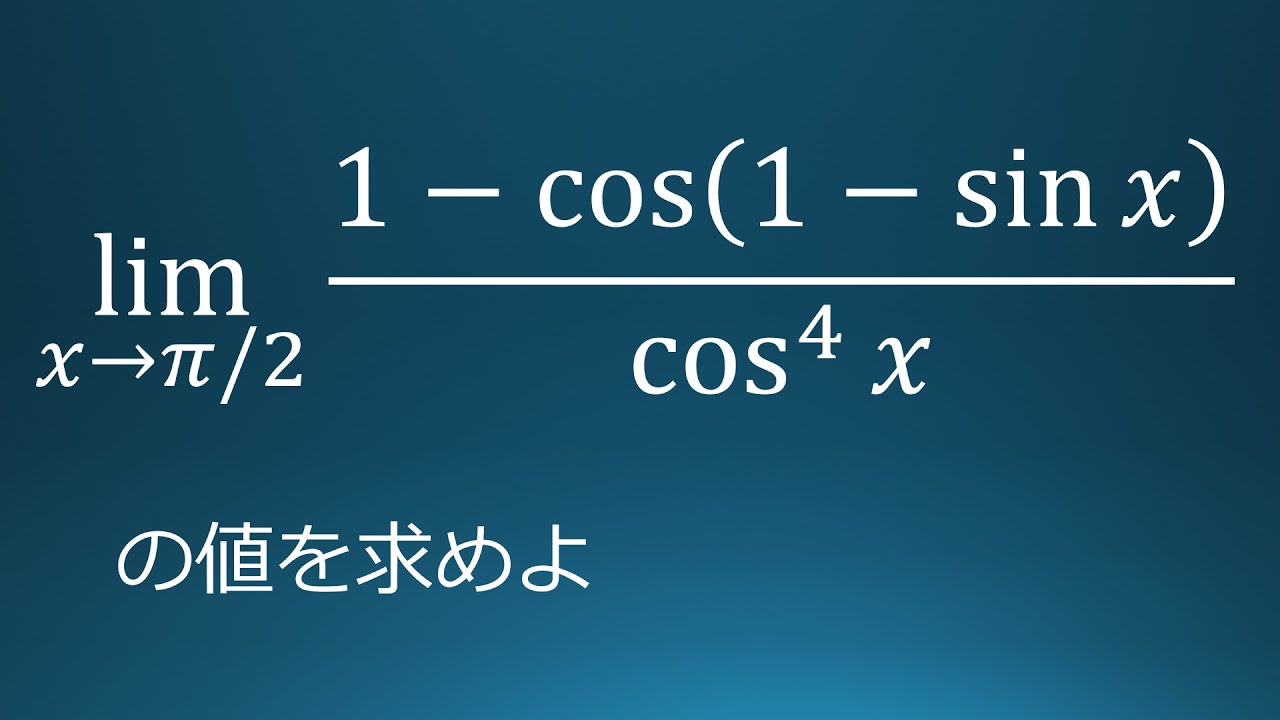
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{x\to\frac{\pi}{2}} \dfrac{1-\cos(1-\sin x)}{\cos^4x}$
これを解け.
この動画を見る
$\displaystyle \lim_{x\to\frac{\pi}{2}} \dfrac{1-\cos(1-\sin x)}{\cos^4x}$
これを解け.
