 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
高知大(医)整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数$(p,q)$の組は何個あるか.
①$p^2-q^2=250$
②$p^2-q^2=210000$
2020高知大(医)過去問
この動画を見る
整数$(p,q)$の組は何個あるか.
①$p^2-q^2=250$
②$p^2-q^2=210000$
2020高知大(医)過去問
17兵庫県教員採用試験(数学:1-1 場合の下図)

単元:
#数A#場合の数と確率#場合の数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(1)
3つの頂点で△を作る。
(1)△は全部で何個
(2)3つの辺が全て異なる△の個数
*図は動画内参照
この動画を見る
1⃣-(1)
3つの頂点で△を作る。
(1)△は全部で何個
(2)3つの辺が全て異なる△の個数
*図は動画内参照
17兵庫県教員採用試験(数学:1-2番 不等式)

単元:
#2次関数#2次方程式と2次不等式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(2)
$x^2-(2a+3)x+6a<0$を満たす整数解が3つとなるaの範囲
この動画を見る
1⃣-(2)
$x^2-(2a+3)x+6a<0$を満たす整数解が3つとなるaの範囲
17兵庫県教員採用試験(数学:1-3番 剰余の定理)
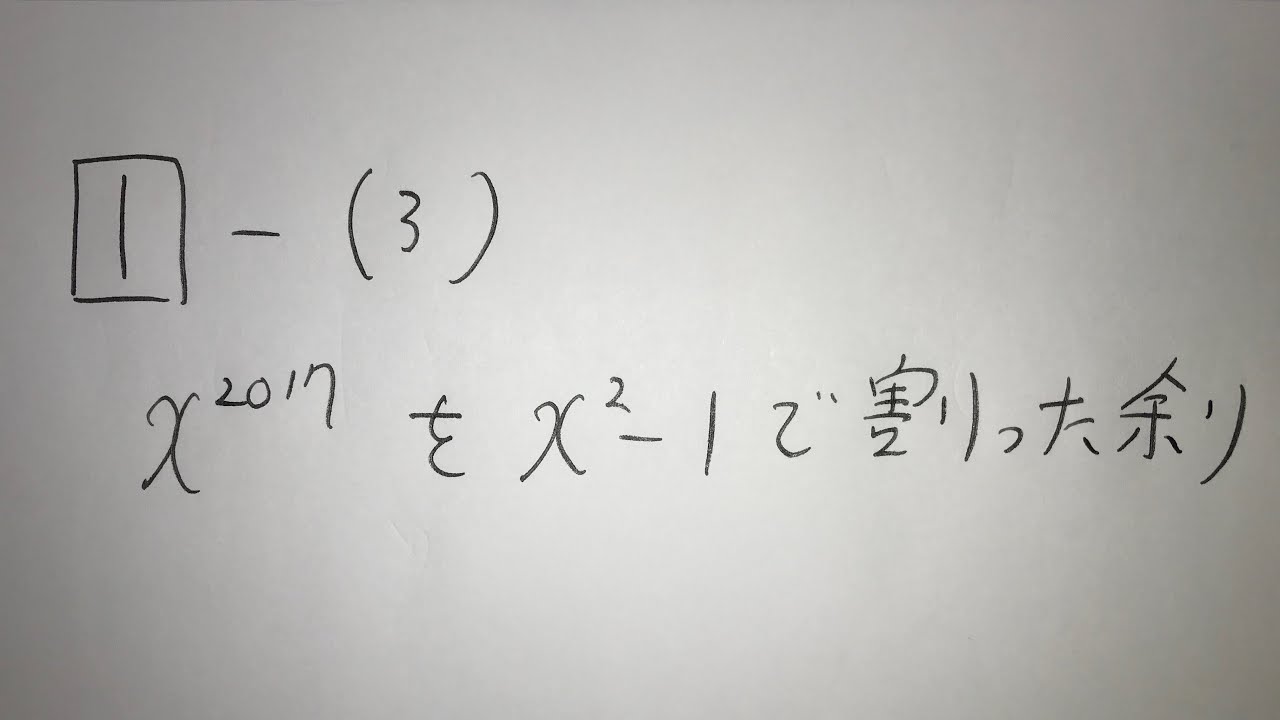
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(3)
$x^{2017}$を$x^2-1$で割った余り
この動画を見る
1⃣-(3)
$x^{2017}$を$x^2-1$で割った余り
19兵庫県教員採用試験(数学:1-3番 命題)
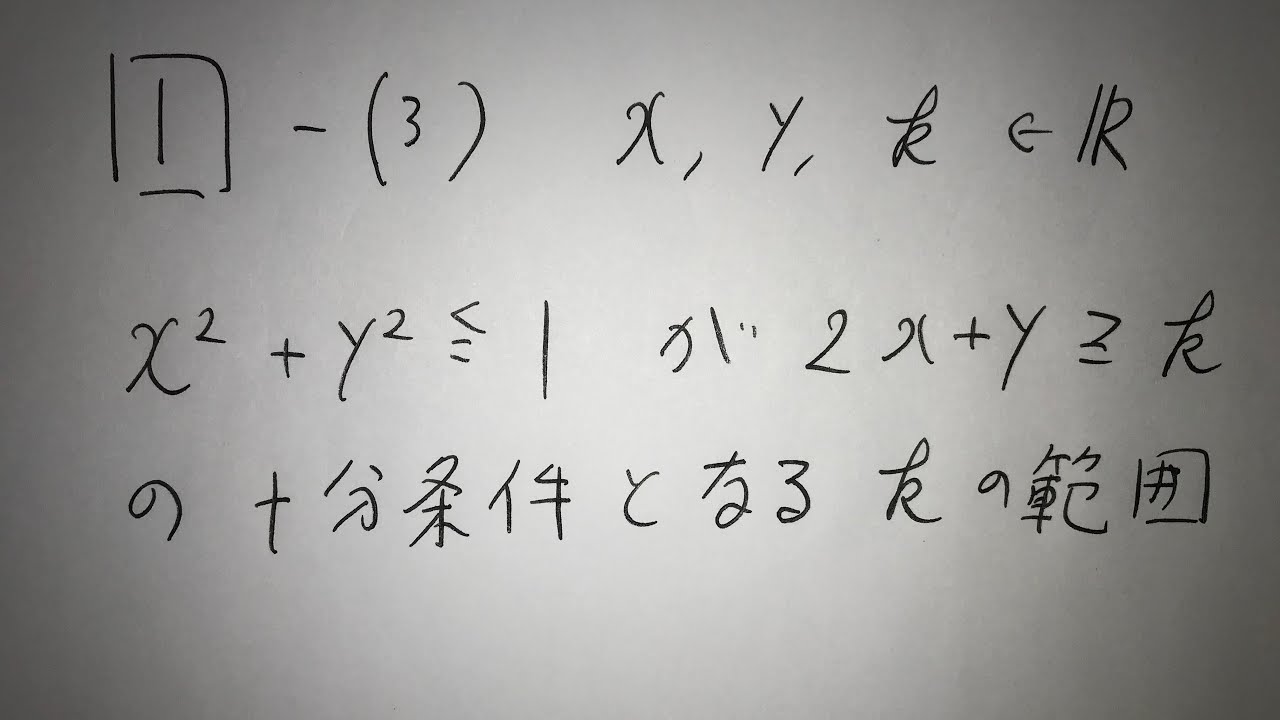
単元:
#数Ⅰ#数Ⅱ#数と式#集合と命題(集合・命題と条件・背理法)#図形と方程式#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
1⃣-(3)
$x,y,k \in \mathbb{ R }$
$x^2+y^2 \leqq 1$が$2x+y \geqq k$の十分条件となるkの範囲
この動画を見る
1⃣-(3)
$x,y,k \in \mathbb{ R }$
$x^2+y^2 \leqq 1$が$2x+y \geqq k$の十分条件となるkの範囲
慶應(医)三次方程式の解とΣ
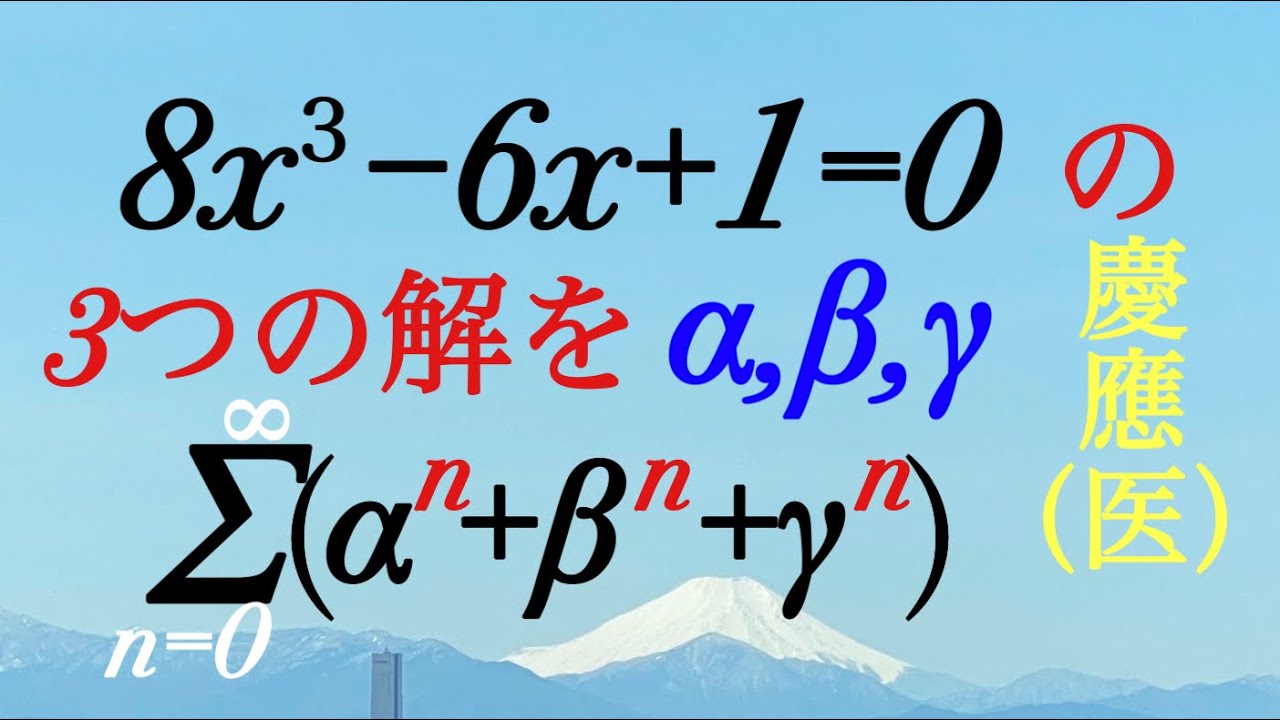
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$8x^3-6x+1=0$の3つの解を$\alpha,\beta,\delta$とする.これを解け.
$\displaystyle \sum_{n=0}^{\infty}(\alpha^n+\beta^n+\delta^n)$
1993慶應(医)
この動画を見る
$8x^3-6x+1=0$の3つの解を$\alpha,\beta,\delta$とする.これを解け.
$\displaystyle \sum_{n=0}^{\infty}(\alpha^n+\beta^n+\delta^n)$
1993慶應(医)
【高校数学】独立な試行の確率~イメージでいけんじゃね?~ 2-5【数学A】

お茶の水女子大 不定方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2x+25y=1993$を満たす整数$x,y$のうち,$x$と$y$の差の絶対値が最小となる$x,y$を求めよ.
お茶の水女子大過去問
この動画を見る
$2x+25y=1993$を満たす整数$x,y$のうち,$x$と$y$の差の絶対値が最小となる$x,y$を求めよ.
お茶の水女子大過去問
ムダが無い英語学習プロセス~いつ単語、文法、長文、リスニング、和訳、英作をするか?【篠原好】

単元:
#その他#英語(高校生)#会話文・イディオム・構文・英単語#英作文#長文読解#英単語#英語リスニング・スピーキング#勉強法#リスニング#数学(高校生)
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
いつ単語、文法、長文、リスニング、和訳、英作をするか?
「ムダが無い英語学習プロセス」についてお話しています。
この動画を見る
いつ単語、文法、長文、リスニング、和訳、英作をするか?
「ムダが無い英語学習プロセス」についてお話しています。
京都府立医大 二次関数の最大値

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m$は自然数の定数である.
$f(x)=-(m+1)x^2+(m^2+3)x$
変数$x$が整数値のみとるときの$f(x)$の最大値を求めよ.
1993京都府立医大過去問
この動画を見る
$m$は自然数の定数である.
$f(x)=-(m+1)x^2+(m^2+3)x$
変数$x$が整数値のみとるときの$f(x)$の最大値を求めよ.
1993京都府立医大過去問
【高校数学】確率の基本性質~余事象の確率~ 2-4【数学A】

単元:
#数A#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
15本のくじの中に当たりくじが5本ある。
この中から2本のくじを同時に引くとき、少なくとも1本は当たる確率を求めよ。
この動画を見る
15本のくじの中に当たりくじが5本ある。
この中から2本のくじを同時に引くとき、少なくとも1本は当たる確率を求めよ。
上智大 住宅ローンは月々いくら?

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
年利$5$%で毎年1万円積立預金20万円を超えるのは何年後か.
$\log_{10}2=0.3010$
$\log_{10}3=0.4771$
$\log_{10}7=0.8450$
2018上智大過去問
この動画を見る
年利$5$%で毎年1万円積立預金20万円を超えるのは何年後か.
$\log_{10}2=0.3010$
$\log_{10}3=0.4771$
$\log_{10}7=0.8450$
2018上智大過去問
【数Ⅲ-155】定積分の部分積分法①

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数Ⅲ(定積分の部分積分法①)
Q次の定積分の値を求めよ。
①$\int_0^{\pi}x \sin x\ dx$
➁$\int_0^{1}xe^{-2x}\ dx$
③$\int_1^e\log x\ dx$
この動画を見る
数Ⅲ(定積分の部分積分法①)
Q次の定積分の値を求めよ。
①$\int_0^{\pi}x \sin x\ dx$
➁$\int_0^{1}xe^{-2x}\ dx$
③$\int_1^e\log x\ dx$
早稲田(教)極限

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
①$\displaystyle \lim_{n\to\infty} \vert 1+\dfrac{i}{n} \vert^n$
②$\left(1+\dfrac{i}{n}\right)^n$の実部を$a_n$,虚部を$b_n$でとする.
$\displaystyle \lim_{n\to \infty}a_n,\displaystyle \lim_{n\to \infty}b_n$を求めよ.
2018早稲田(教)過去問
この動画を見る
①$\displaystyle \lim_{n\to\infty} \vert 1+\dfrac{i}{n} \vert^n$
②$\left(1+\dfrac{i}{n}\right)^n$の実部を$a_n$,虚部を$b_n$でとする.
$\displaystyle \lim_{n\to \infty}a_n,\displaystyle \lim_{n\to \infty}b_n$を求めよ.
2018早稲田(教)過去問
17東京都教員採用試験(数学 1-2 方程式)

単元:
#数Ⅰ#数Ⅱ#数と式#式と証明#式の計算(整式・展開・因数分解)#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
1⃣-(2)
$x^3+\frac{1}{x^3}=0$のとき、$x+\frac{1}{x}$の値を求めよ。
この動画を見る
1⃣-(2)
$x^3+\frac{1}{x^3}=0$のとき、$x+\frac{1}{x}$の値を求めよ。
17東京都教員採用試験(数学1-1番 整数問題)
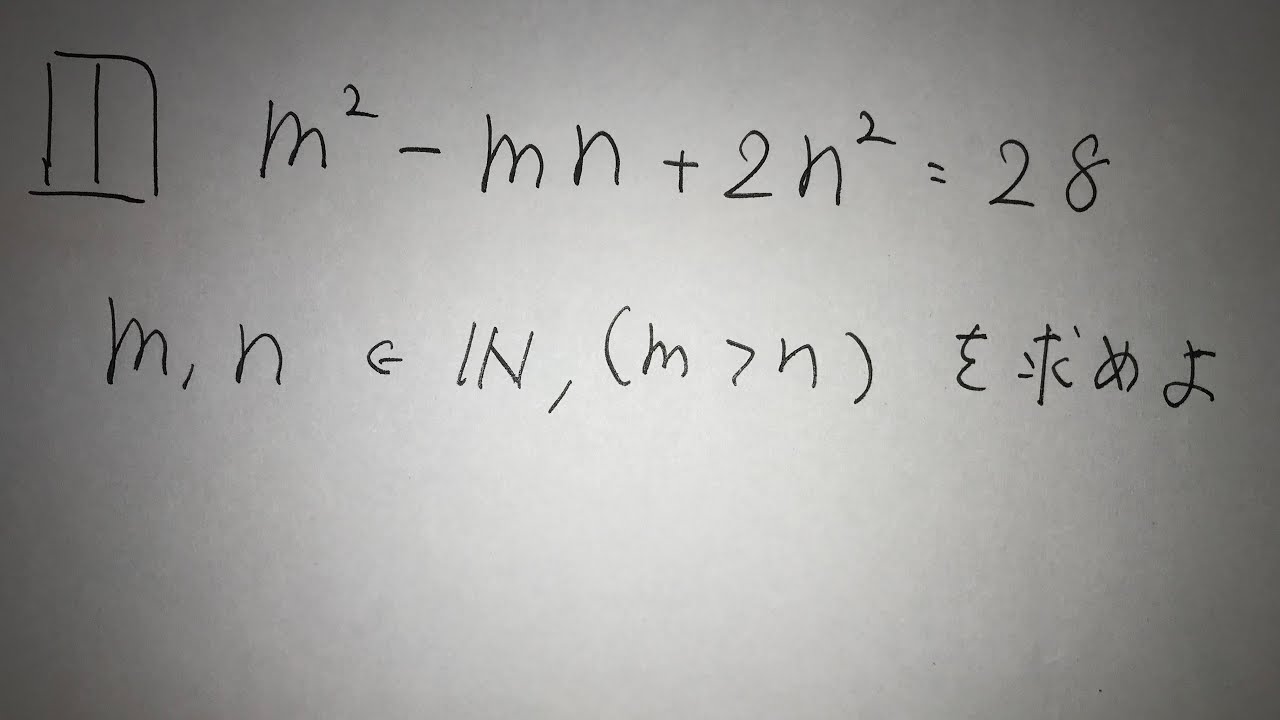
単元:
#数Ⅰ#数A#数Ⅱ#2次関数#式と証明#2次方程式と2次不等式#整数の性質#約数・倍数・整数の割り算と余り・合同式#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
1⃣$m^2-mn+2n^2=28$
$m,n \in \mathbb{ N } (m>n)$を求めよ。
この動画を見る
1⃣$m^2-mn+2n^2=28$
$m,n \in \mathbb{ N } (m>n)$を求めよ。
整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \sum_{k=1}^n k!=m^2$を満たす自然数$(m,n)$をすべて求めよ.
この動画を見る
$\displaystyle \sum_{k=1}^n k!=m^2$を満たす自然数$(m,n)$をすべて求めよ.
【高校数学】確率の基本性質~和事象の確率~ 2-3【数学A】

単元:
#数A#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1から9までの番号をつけたカードが各数字3枚ずつ計27枚ある。
このカードから2枚を取り出すとき、2枚が同じ数字か2枚の数字の和が5以下である確率を求めよ。
この動画を見る
1から9までの番号をつけたカードが各数字3枚ずつ計27枚ある。
このカードから2枚を取り出すとき、2枚が同じ数字か2枚の数字の和が5以下である確率を求めよ。
19東京都教員採用試験(数学:3番x軸回転の体積)

単元:
#数Ⅱ#微分法と積分法#面積、体積#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
3⃣$f(x)=x \sqrt{4-x^2} \quad (0 \leqq x \leqq 2)$とy=xで囲まれた領域Sの回転体の体積Vを求めよ。
(1)y=f(x)の最大値
(2)y=xと$y=x \sqrt{4-x^2}$ $(0 \leqq x \leqq 2)$で囲まれたSの値を求めよ。
(3)Sの回転体の体積V
この動画を見る
3⃣$f(x)=x \sqrt{4-x^2} \quad (0 \leqq x \leqq 2)$とy=xで囲まれた領域Sの回転体の体積Vを求めよ。
(1)y=f(x)の最大値
(2)y=xと$y=x \sqrt{4-x^2}$ $(0 \leqq x \leqq 2)$で囲まれたSの値を求めよ。
(3)Sの回転体の体積V
ガウス記号

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$[(6+3\sqrt3)^{2020}]$を$3^{2020}$で割った余りを求めよ.
この動画を見る
$[(6+3\sqrt3)^{2020}]$を$3^{2020}$で割った余りを求めよ.
【高校数学】確率の基本性質~排反~ 2-2 【数学A】

【数Ⅰ】数と式: √(6-√32)の2重根号を外す!

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\sqrt{(6-\sqrt{32})}$の2重根号を外しなさい
この動画を見る
$\sqrt{(6-\sqrt{32})}$の2重根号を外しなさい
整数問題
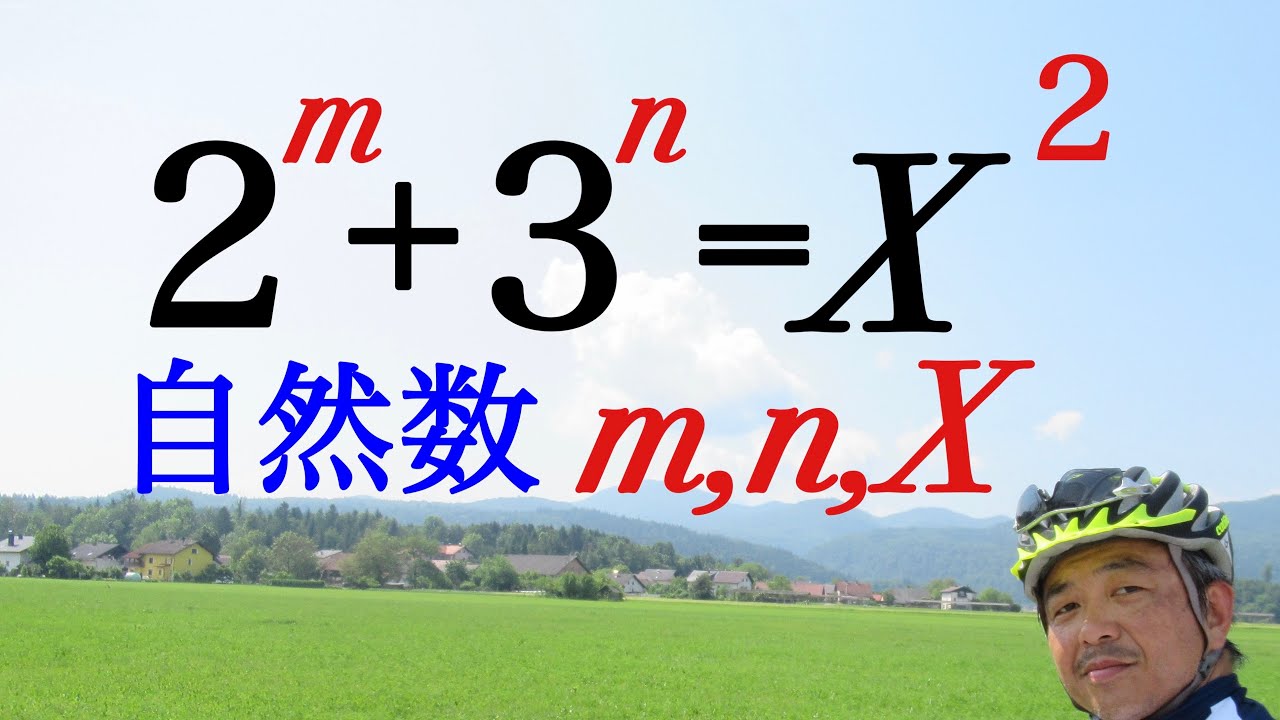
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m,n,X$は自然数である.これを解け.
$2^m+3^n=X^2$
この動画を見る
$m,n,X$は自然数である.これを解け.
$2^m+3^n=X^2$
【高校数学】確率の例題~少し難しいやつ~ 2-1.5 【数学A】

単元:
#数A#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
5人がじゃんけんを1回するとき、次の確率を求めよ。
(a) 1人だけが勝つ確率
(b) 3人が勝つ確率
(c) あいこになる確率
-----------------
2⃣
赤玉と白玉が合わせて8個入った袋がある。
この袋の中から玉を2個同時に取り出すとき、赤玉の出ない確率が$\displaystyle \frac{5}{14}$こであるという。
袋の中には白玉は何個入っているか。
この動画を見る
1⃣
5人がじゃんけんを1回するとき、次の確率を求めよ。
(a) 1人だけが勝つ確率
(b) 3人が勝つ確率
(c) あいこになる確率
-----------------
2⃣
赤玉と白玉が合わせて8個入った袋がある。
この袋の中から玉を2個同時に取り出すとき、赤玉の出ない確率が$\displaystyle \frac{5}{14}$こであるという。
袋の中には白玉は何個入っているか。
整数問題 分数式
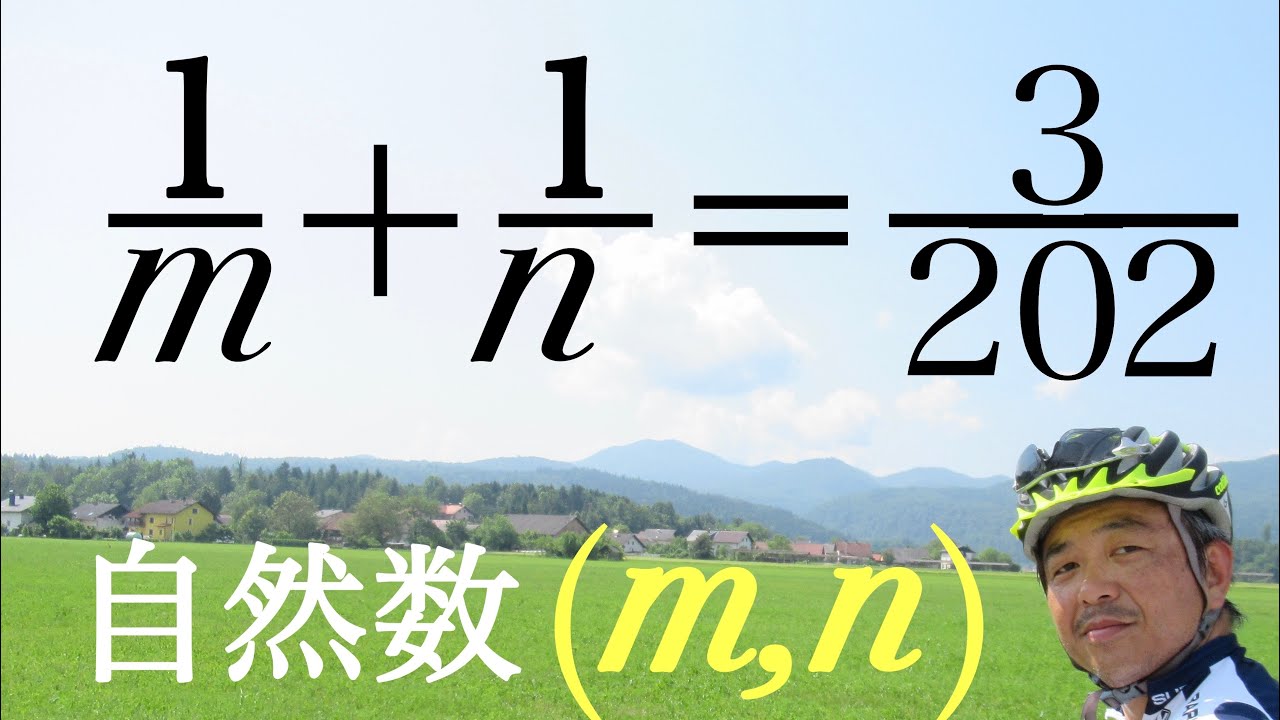
単元:
#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m,n$は自然数である.
$\dfrac{1}{m}+\dfrac{1}{n}=\dfrac{3}{202}$
$(m,n)$をすべて求めよ.
この動画を見る
$m,n$は自然数である.
$\dfrac{1}{m}+\dfrac{1}{n}=\dfrac{3}{202}$
$(m,n)$をすべて求めよ.
京大卒しか入手できないゴリゴリの内部資料を公開【篠原好】

整数問題 ピタゴラス数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b,c$は自然数である.
$a,b,c$の最大公約数は1であり,$a^2+b^2=c^2$とする.
(1)$a,b$はどちらかは3の倍数であることを示せ.
(2)$a,b$はどちらかは4の倍数であることを示せ.
(3)$a,b,c$のどれかは5の倍数であることを示せ.
この動画を見る
$a,b,c$は自然数である.
$a,b,c$の最大公約数は1であり,$a^2+b^2=c^2$とする.
(1)$a,b$はどちらかは3の倍数であることを示せ.
(2)$a,b$はどちらかは4の倍数であることを示せ.
(3)$a,b,c$のどれかは5の倍数であることを示せ.
首都大学東京 漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \sum_{k=1}^n a_k=n^4+6n^3+11n^2+6n$
①$a_n$を$n$の式で表せ.
②$\displaystyle \sum_{k=1}^{\infty}\dfrac{1}{a_k}$
2018首都大学東京過去問
この動画を見る
$\displaystyle \sum_{k=1}^n a_k=n^4+6n^3+11n^2+6n$
①$a_n$を$n$の式で表せ.
②$\displaystyle \sum_{k=1}^{\infty}\dfrac{1}{a_k}$
2018首都大学東京過去問
息抜き整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
次の数はすべて整数であるとき,これを解け.
$\sqrt[3]{4913}$
$\sqrt[3]{79507}$
$\sqrt[3]{314432}$
この動画を見る
次の数はすべて整数であるとき,これを解け.
$\sqrt[3]{4913}$
$\sqrt[3]{79507}$
$\sqrt[3]{314432}$
【数Ⅰ】2次関数:放物線y=x²-6x+10をx軸、y軸、原点に関してそれぞれ対称移動して得られる放物線の方程式を求めましょう。

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
放物線$y=x²-6x+10$をx軸、y軸、原点に関してそれぞれ対称移動して得られる放物線の方程式を求めなさい
この動画を見る
放物線$y=x²-6x+10$をx軸、y軸、原点に関してそれぞれ対称移動して得られる放物線の方程式を求めなさい
