 神奈川県公立高校入試
神奈川県公立高校入試
 神奈川県公立高校入試
神奈川県公立高校入試
食塩水 2024神奈川県

単元:
#数学(中学生)#中1数学#方程式#高校入試過去問(数学)#神奈川県公立高校入試#神奈川県公立高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
4%の食塩水300gが入ったビーカーから食塩水$a$gを取り出した。
その後ビーカーに残っている食塩水に食塩$a$gを加えてよくかき混ぜたところ12%の食塩水になった。
$a$を求めよ。
この動画を見る
4%の食塩水300gが入ったビーカーから食塩水$a$gを取り出した。
その後ビーカーに残っている食塩水に食塩$a$gを加えてよくかき混ぜたところ12%の食塩水になった。
$a$を求めよ。
【中学数学】高校入試:2022年度神奈川県立高校入試数学大問2

単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
(ア)0.2x+0.8y=1 , (1/2)x+(7/8)y=-2
(イ)4x²-x-2=0
(ウ)y=(-1/4)x² , xの変域が-2≦x≦4のとき,yの変域は?
(エ)A班の生徒と,A班よりも5人少ないB班の生徒で,体育館にイスを並べた。A班の生徒はそれぞれ3脚ずつ並べ、B班の生徒はそれぞれ4脚ずつ並べたところ,A班の生徒が並べたイスの総数はB班の生徒が並べたイスの総数より3脚多かった。A班の生徒の人数を求めなさい。
(オ)x=√6+√3,y=√6-√3 のとき、x²y+xy²の値は?
この動画を見る
(ア)0.2x+0.8y=1 , (1/2)x+(7/8)y=-2
(イ)4x²-x-2=0
(ウ)y=(-1/4)x² , xの変域が-2≦x≦4のとき,yの変域は?
(エ)A班の生徒と,A班よりも5人少ないB班の生徒で,体育館にイスを並べた。A班の生徒はそれぞれ3脚ずつ並べ、B班の生徒はそれぞれ4脚ずつ並べたところ,A班の生徒が並べたイスの総数はB班の生徒が並べたイスの総数より3脚多かった。A班の生徒の人数を求めなさい。
(オ)x=√6+√3,y=√6-√3 のとき、x²y+xy²の値は?
【中学数学】高校入試:2022年度神奈川県立高校入試数学大問5イ別解

単元:
#数学(中学生)#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#高校入試過去問(数学)#神奈川県公立高校入試#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
大,小2つのさいころを同時に1回投げ,大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとする。出た目の数によって,線分PQ上に点Rを,PR:RQ=a:bとなるようにとり,線分PRを1辺とする正方形をX,線分RQを1辺とする正方形をYとし,この2つの正方形の面積を比較する。
(イ) Xの面積がYの面積より25cm²以上大きくなる確率は□である。
この動画を見る
大,小2つのさいころを同時に1回投げ,大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとする。出た目の数によって,線分PQ上に点Rを,PR:RQ=a:bとなるようにとり,線分PRを1辺とする正方形をX,線分RQを1辺とする正方形をYとし,この2つの正方形の面積を比較する。
(イ) Xの面積がYの面積より25cm²以上大きくなる確率は□である。
【中学数学】高校入試:2022年度神奈川県立高校入試数学大問5アイ
単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
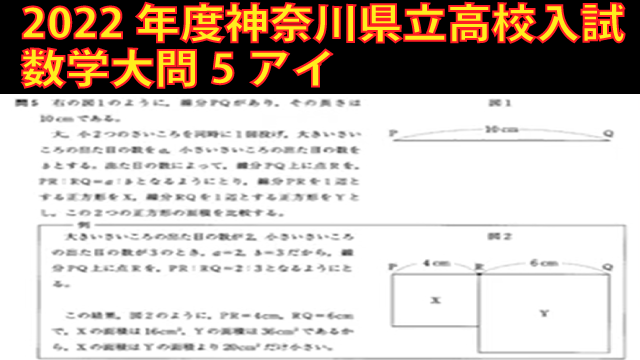
大,小2つのさいころを同時に1回投げ,大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとする。出た目の数によって,線分PQ上に点Rを,PR:RQ=a:bとなるようにとり,線分PRを1辺とする正方形をX,線分RQを1辺とする正方形をYとし,この2つの正方形の面積を比較する。
(ア) Xの面積とYの面積が等しくなる確率は□である。
(イ) Xの面積がYの面積より25cm²以上大きくなる確率は□である。
この動画を見る
大,小2つのさいころを同時に1回投げ,大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとする。出た目の数によって,線分PQ上に点Rを,PR:RQ=a:bとなるようにとり,線分PRを1辺とする正方形をX,線分RQを1辺とする正方形をYとし,この2つの正方形の面積を比較する。
(ア) Xの面積とYの面積が等しくなる確率は□である。
(イ) Xの面積がYの面積より25cm²以上大きくなる確率は□である。
【中学数学】高校入試:2022年度神奈川県立高校入試数学大問4(ウ)

単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
2022年度神奈川県立高校入試数学大問4(ウ)解説していきます.
この動画を見る
2022年度神奈川県立高校入試数学大問4(ウ)解説していきます.
【数学】高校入試:2022年度神奈川県立高校入試数学大問3エ

単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
右の図3において,線分ABは円Oの直径であり,2点C,Dは円Oの周上の点である。
また,点Eは線分AC上の点で,BC//DEであり,点Fは線分ABと線分DEとの交点である。
AE=2cm,CE=1cm,DE=3cmのとき,三角形BDFの面積は□cm²である。
この動画を見る
右の図3において,線分ABは円Oの直径であり,2点C,Dは円Oの周上の点である。
また,点Eは線分AC上の点で,BC//DEであり,点Fは線分ABと線分DEとの交点である。
AE=2cm,CE=1cm,DE=3cmのとき,三角形BDFの面積は□cm²である。
【数学】高校入試:2022年度神奈川県立高校入試数学大問3イ

単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
(イ) ある中学校の,1年生38人,2年生40人,3年生40人が上体起こしを行った。
右の表は,1年生の上体起こしの記録を,度数分布表にまとめたものである。
次の1年生,2年生,3年生の上体起こしの記録に関する説明から,(ⅰ)2年生の上体起こしの記録と,(ⅱ)3年生の上体起こしの記録を,それぞれヒストグラムに表したものとして最も適するものをあとの1~6の中から1つずつ選び、その番号を答えなさい。
この動画を見る
(イ) ある中学校の,1年生38人,2年生40人,3年生40人が上体起こしを行った。
右の表は,1年生の上体起こしの記録を,度数分布表にまとめたものである。
次の1年生,2年生,3年生の上体起こしの記録に関する説明から,(ⅰ)2年生の上体起こしの記録と,(ⅱ)3年生の上体起こしの記録を,それぞれヒストグラムに表したものとして最も適するものをあとの1~6の中から1つずつ選び、その番号を答えなさい。
【数学】高校入試:2022年度神奈川県立高校入試数学大問3ア(ⅱ)

単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
(ア) 右の図1のように,AB<AC,∠ABCが鋭角の平行四辺形ABCDがあり,∠BCDの二等分線と辺ADとの交点をEとする。
また,辺BCの延長上に点Fを,CF=DFとなるようにとる。
さらに,辺CD上に点Gを,CG>GDとなるようにとり,線分DF上に点Hを,DG=DHとなるようにとる。
このとき,四角形CFDEが平行四辺形になるときの,∠ABCの大きさとして正しいものを次の1~4の中から1つ選び,その番号を答えなさい。
1.45° 2.50° 3.55° 4.60°
この動画を見る
(ア) 右の図1のように,AB<AC,∠ABCが鋭角の平行四辺形ABCDがあり,∠BCDの二等分線と辺ADとの交点をEとする。
また,辺BCの延長上に点Fを,CF=DFとなるようにとる。
さらに,辺CD上に点Gを,CG>GDとなるようにとり,線分DF上に点Hを,DG=DHとなるようにとる。
このとき,四角形CFDEが平行四辺形になるときの,∠ABCの大きさとして正しいものを次の1~4の中から1つ選び,その番号を答えなさい。
1.45° 2.50° 3.55° 4.60°
【数学】高校入試:2022年度神奈川県立高校入試数学大問3ア(ⅰ)

単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
(ア) 右の図1のように,AB<AC,∠ABCが鋭角の平行四辺形ABCDがあり,∠BCDの二等分線と辺ADとの交点をEとする。
また,辺BCの延長上に点Fを,CF=DFとなるようにとる。
さらに,辺CD上に点Gを,CG>GDとなるようにとり,線分DF上に点Hを,DG=DHとなるようにとる。
このとき,三角形DEGと三角形DCHが合同であることを証明しなさい。
この動画を見る
(ア) 右の図1のように,AB<AC,∠ABCが鋭角の平行四辺形ABCDがあり,∠BCDの二等分線と辺ADとの交点をEとする。
また,辺BCの延長上に点Fを,CF=DFとなるようにとる。
さらに,辺CD上に点Gを,CG>GDとなるようにとり,線分DF上に点Hを,DG=DHとなるようにとる。
このとき,三角形DEGと三角形DCHが合同であることを証明しなさい。
【数学】高校入試:2022年度神奈川県立高校入試数学大問4(ア)(イ)

単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
問4 右の図において、直線①は関数$y=x+3$のグラフであり、曲線②は関数$y=ax^2$のグラフである。 点Aは直線①と曲線②との交点で、そのx座標は6である。点Bは曲線②状の点で、線分ABはx軸に平行である。点Cは直線①上の点で、線分BCはy軸に平行である。
また、点Dは線分BCとx軸との交点である。
さらに、減点をOとするとき、点Eはx軸上の点で、$DO:OE=6:5$であり、そのx座標は正である。このとき、次の問いに答えなさい。
(ア)曲線②の式y=ax²のaの値として正しいものを次の1~6の中から1つ選び、その番号を答えなさい。
1.$a=\dfrac{1}{6}$ 2.$a=\dfrac{1}{4}$ 3.$a=\dfrac{1}{3}$ 4.$a=\dfrac{1}{2}$ 5.$a=\dfrac{3}{4}$ 6.$a=\dfrac{3}{2}$
(イ)直線CEの式をy=mx+nとするとき、(ⅰ)mの値と、(ⅱ)nの値として正しいものを、それぞれ次の1~6の中から1つずつ選び、その番号を答えなさい。
(ⅰ)mの値
1.$m=\dfrac{3}{13}$ 2.$m=\dfrac{1}{4}$ 3.$m=\dfrac{3}{11}$ 4.$m=\dfrac{3}{10}$ 5.$m=\dfrac{1}{3}$ 6.$m=\dfrac{3}{8}$
(ⅱ)nの値
1.$n=\dfrac{-17}{11}$ 2.$n=\dfrac{-20}{13}$ 3.$n=\dfrac{-3}{2}$
4.$n=\dfrac{-18}{13}$ 5.$n=\dfrac{-15}{11}$ 6.$n=\dfrac{-11}{10}$
この動画を見る
問4 右の図において、直線①は関数$y=x+3$のグラフであり、曲線②は関数$y=ax^2$のグラフである。 点Aは直線①と曲線②との交点で、そのx座標は6である。点Bは曲線②状の点で、線分ABはx軸に平行である。点Cは直線①上の点で、線分BCはy軸に平行である。
また、点Dは線分BCとx軸との交点である。
さらに、減点をOとするとき、点Eはx軸上の点で、$DO:OE=6:5$であり、そのx座標は正である。このとき、次の問いに答えなさい。
(ア)曲線②の式y=ax²のaの値として正しいものを次の1~6の中から1つ選び、その番号を答えなさい。
1.$a=\dfrac{1}{6}$ 2.$a=\dfrac{1}{4}$ 3.$a=\dfrac{1}{3}$ 4.$a=\dfrac{1}{2}$ 5.$a=\dfrac{3}{4}$ 6.$a=\dfrac{3}{2}$
(イ)直線CEの式をy=mx+nとするとき、(ⅰ)mの値と、(ⅱ)nの値として正しいものを、それぞれ次の1~6の中から1つずつ選び、その番号を答えなさい。
(ⅰ)mの値
1.$m=\dfrac{3}{13}$ 2.$m=\dfrac{1}{4}$ 3.$m=\dfrac{3}{11}$ 4.$m=\dfrac{3}{10}$ 5.$m=\dfrac{1}{3}$ 6.$m=\dfrac{3}{8}$
(ⅱ)nの値
1.$n=\dfrac{-17}{11}$ 2.$n=\dfrac{-20}{13}$ 3.$n=\dfrac{-3}{2}$
4.$n=\dfrac{-18}{13}$ 5.$n=\dfrac{-15}{11}$ 6.$n=\dfrac{-11}{10}$
【中学数学】高校入試:2022年度神奈川県立高校入試数学大問6(ウ)

単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
AB=5cm,BC=1cm,AD=4m,∠ADC=∠BCD=90°の台形ABCDを底面とし,AE=BF=CG=DH=1cmを高さとする四角柱である。
点Iが辺CD上の点で,CI:ID=7:3であるとき,この四角柱の表面上に,図2のように点Aから辺EF,辺GHと交わるように,点Iまで線を引く。このような線のうち,長さが最も短くなるように引いた線の長さは√□cmである。
この動画を見る
AB=5cm,BC=1cm,AD=4m,∠ADC=∠BCD=90°の台形ABCDを底面とし,AE=BF=CG=DH=1cmを高さとする四角柱である。
点Iが辺CD上の点で,CI:ID=7:3であるとき,この四角柱の表面上に,図2のように点Aから辺EF,辺GHと交わるように,点Iまで線を引く。このような線のうち,長さが最も短くなるように引いた線の長さは√□cmである。
【数学】高校入試:2022年度神奈川県立高校入試数学大問6(イ)

単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
AB=5cm,BC=1cm,AD=4m,∠ADC=∠BCD=90°の台形ABCDを底面とし,AE=BF=CG=DH=1cmを高さとする四角柱である。
(イ)この四角柱において,3点B,D,Gを結んでできる三角形の面積として正しいものを答えなさい。
この動画を見る
AB=5cm,BC=1cm,AD=4m,∠ADC=∠BCD=90°の台形ABCDを底面とし,AE=BF=CG=DH=1cmを高さとする四角柱である。
(イ)この四角柱において,3点B,D,Gを結んでできる三角形の面積として正しいものを答えなさい。
【数学】高校入試:2022年度神奈川県立高校入試数学大問6(ア)

単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
AB=5cm,BC=1cm,AD=4m,∠ADC=∠BCD=90°の台形ABCDを底面とし,AE=BF=CG=DH=1cmを高さとする四角柱である。
(ア) この四角柱の体積として正しいものを選びなさい
この動画を見る
AB=5cm,BC=1cm,AD=4m,∠ADC=∠BCD=90°の台形ABCDを底面とし,AE=BF=CG=DH=1cmを高さとする四角柱である。
(ア) この四角柱の体積として正しいものを選びなさい
【中学数学】円周上の角度を求める問題~神奈川県公立高校入試2021~【高校受験】
【数学力!複雑なだけが応用じゃない!】図形:神奈川県公立高校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
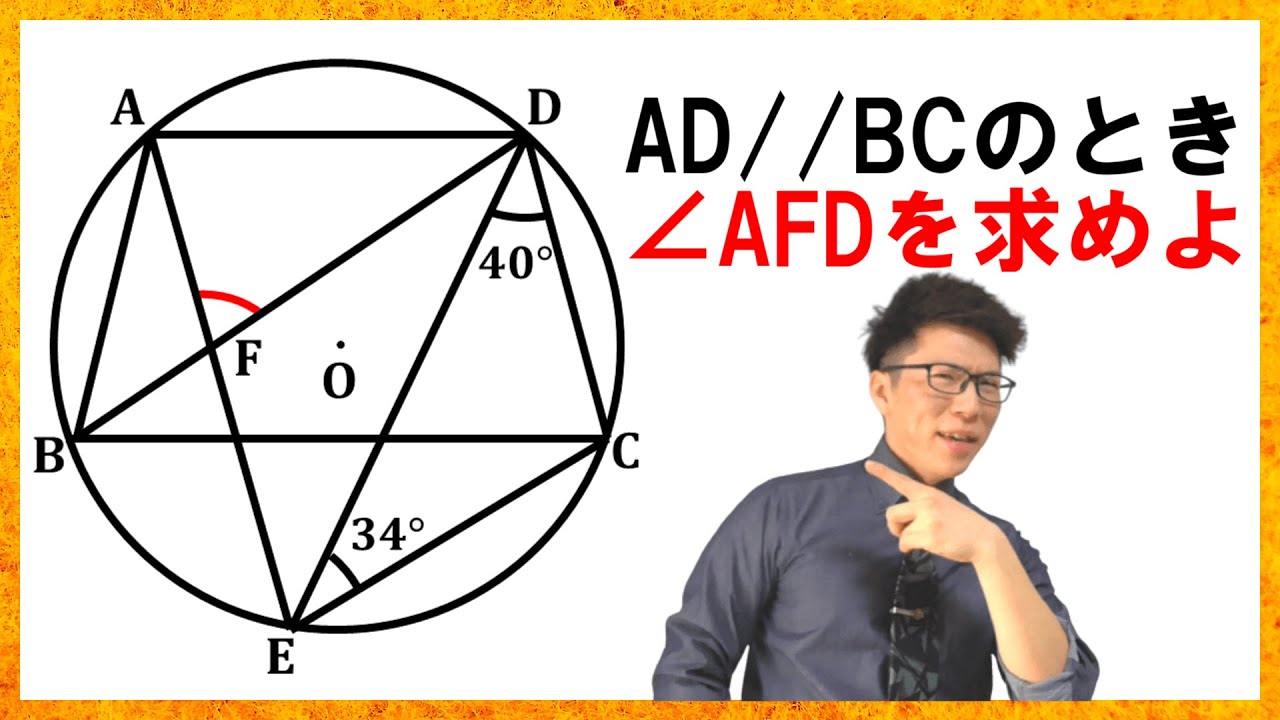
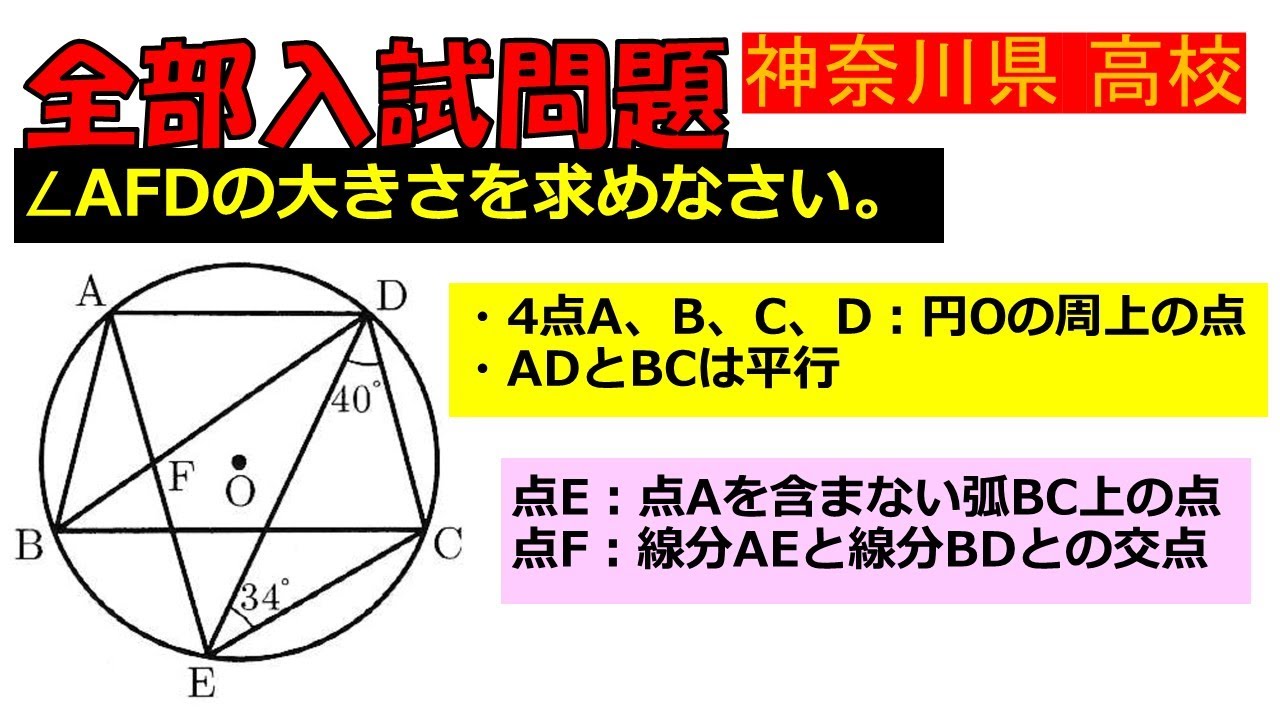
入試問題 神奈川県の公立高等学校
$\angle AFDの大きさを求めなさい。
・4点A、B、C、D:円○の周上の点
・ADとBCは平行
点E:点Aを含まない弧BC上の点
点F:線分AEと線分BDとの交点
※図は動画内参照
この動画を見る
入試問題 神奈川県の公立高等学校
$\angle AFDの大きさを求めなさい。
・4点A、B、C、D:円○の周上の点
・ADとBCは平行
点E:点Aを含まない弧BC上の点
点F:線分AEと線分BDとの交点
※図は動画内参照
【問題との付き合い方】因数分解・二次方程式:神奈川県公立高等学校~全国入試問題解法【選択式】

単元:
#数学(中学生)#式の計算(展開、因数分解)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 神奈川県の公立高等学校
$(x+6)^2-5(x+6)-24$
を因数分解しなさい。
【2次方程式】
$x^2-3x+1=0$
を解きなさい。
この動画を見る
入試問題 神奈川県の公立高等学校
$(x+6)^2-5(x+6)-24$
を因数分解しなさい。
【2次方程式】
$x^2-3x+1=0$
を解きなさい。
【中学数学】確率の演習~神奈川県公立高校入試標準問題2020~【高校受験】

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
【神奈川県公立高校入試標準問題2020】確率の演習
この動画を見る
【神奈川県公立高校入試標準問題2020】確率の演習
