 明治大学付属明治高等学校
明治大学付属明治高等学校
 明治大学付属明治高等学校
明治大学付属明治高等学校
三角形に内接する正方形 明大明治
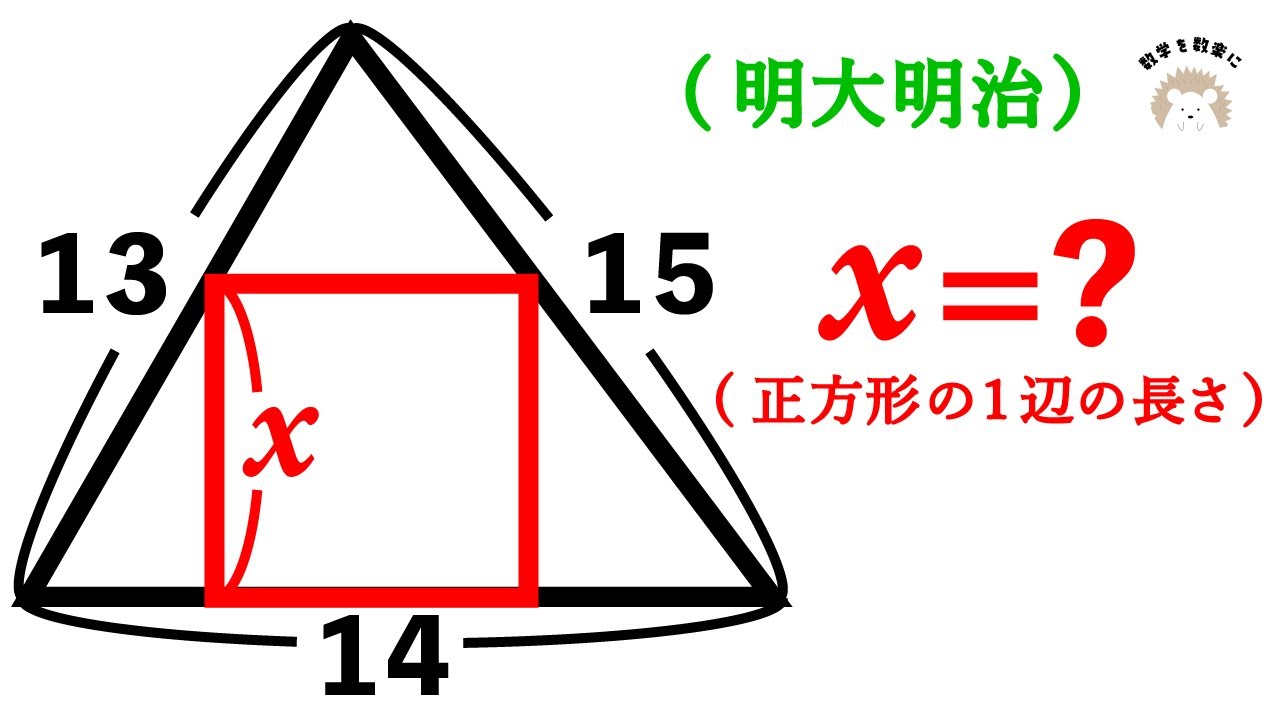
三角形に内接する正方形 明大明治

単元:
#数学(中学生)#中1数学#中2数学#中3数学#相似な図形#平面図形#三角形と四角形#高校入試過去問(数学)#明治大学付属明治高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
x=?(正方形の1辺の長さ)
この動画を見る
x=?(正方形の1辺の長さ)
【アナタならどうする…!?】連立方程式:明治大学付属明治高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#明治大学付属明治高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x^2-4y^2-10x+25=0 ・・・① \\
x^2+x-6-2xy+4y=0・・・②
\end{array}
\right.
\end{eqnarray}$
上式が成り立つ$ x,y $の組をすべて求めよ.
明治大学付属明治高等学校過去問
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x^2-4y^2-10x+25=0 ・・・① \\
x^2+x-6-2xy+4y=0・・・②
\end{array}
\right.
\end{eqnarray}$
上式が成り立つ$ x,y $の組をすべて求めよ.
明治大学付属明治高等学校過去問
【まずは解くこと…!】文字式:明治大学付属明治高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#平方根#高校入試過去問(数学)#明治大学付属明治高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
\sqrt2x+\sqrt7y=3 \\
\sqrt7x-\sqrt2y=-6
\end{array}
\right.
\end{eqnarray}$
のとき,$ y-x=\Box $
明治大学付属明治高等学校過去問
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
\sqrt2x+\sqrt7y=3 \\
\sqrt7x-\sqrt2y=-6
\end{array}
\right.
\end{eqnarray}$
のとき,$ y-x=\Box $
明治大学付属明治高等学校過去問
【数学】2次関数:明大明治2020年度大問5 解説

単元:
#数学(中学生)#高校入試過去問(数学)#明治大学付属明治高等学校
指導講師:
理数個別チャンネル
問題文全文(内容文):
2次関数$y=-ⅹ^2$上に点A,Bがあり、点Aのⅹ座標をaとすると直線ℓはー2a+1となった。この時の点Bの座標をa,を用いて表せ。【明大明治 過去問 2020】【二次関数】
この動画を見る
2次関数$y=-ⅹ^2$上に点A,Bがあり、点Aのⅹ座標をaとすると直線ℓはー2a+1となった。この時の点Bの座標をa,を用いて表せ。【明大明治 過去問 2020】【二次関数】
【5分で知る!証明問題のストーリー!】整数:明治大学付属中野高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#高校入試過去問(数学)#明治大学付属明治高等学校#明治大学付属中野高等学校#明治大学付属中野高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 明治大学付属中野高等学校
3けたの正の整数において、上2けたの数から一の位の数を
引いた数が11の倍数
もとの3けたの 整数は、11の倍数 である。
この性質が成り立つわけを説明しなさい。
※3けたの正の整数の百の位の数をx、十の位の数をy、一の位の数をzとする
この動画を見る
入試問題 明治大学付属中野高等学校
3けたの正の整数において、上2けたの数から一の位の数を
引いた数が11の倍数
もとの3けたの 整数は、11の倍数 である。
この性質が成り立つわけを説明しなさい。
※3けたの正の整数の百の位の数をx、十の位の数をy、一の位の数をzとする
【みんな大好き】因数分解:明治大学付属明治高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#明治大学付属明治高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 明治大学付属明治高等学校
$(x-6y+3z)(x+2y-z)+5z(4y-z)-20y^2$
を因数分解すると▭である。
この動画を見る
入試問題 明治大学付属明治高等学校
$(x-6y+3z)(x+2y-z)+5z(4y-z)-20y^2$
を因数分解すると▭である。
二次方程式:明治大学付属明治高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#明治大学付属明治高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 明治大学付属明治高等学校
$x$についての$2$次方程式
$x^2 - (a^2 - 4a + 5) x + 5a(a – 4) = 0$
($a$が正の整数)
解が1つ になる。→ $a$の値を求めよ。
この動画を見る
入試問題 明治大学付属明治高等学校
$x$についての$2$次方程式
$x^2 - (a^2 - 4a + 5) x + 5a(a – 4) = 0$
($a$が正の整数)
解が1つ になる。→ $a$の値を求めよ。
2012明大明治の問題!
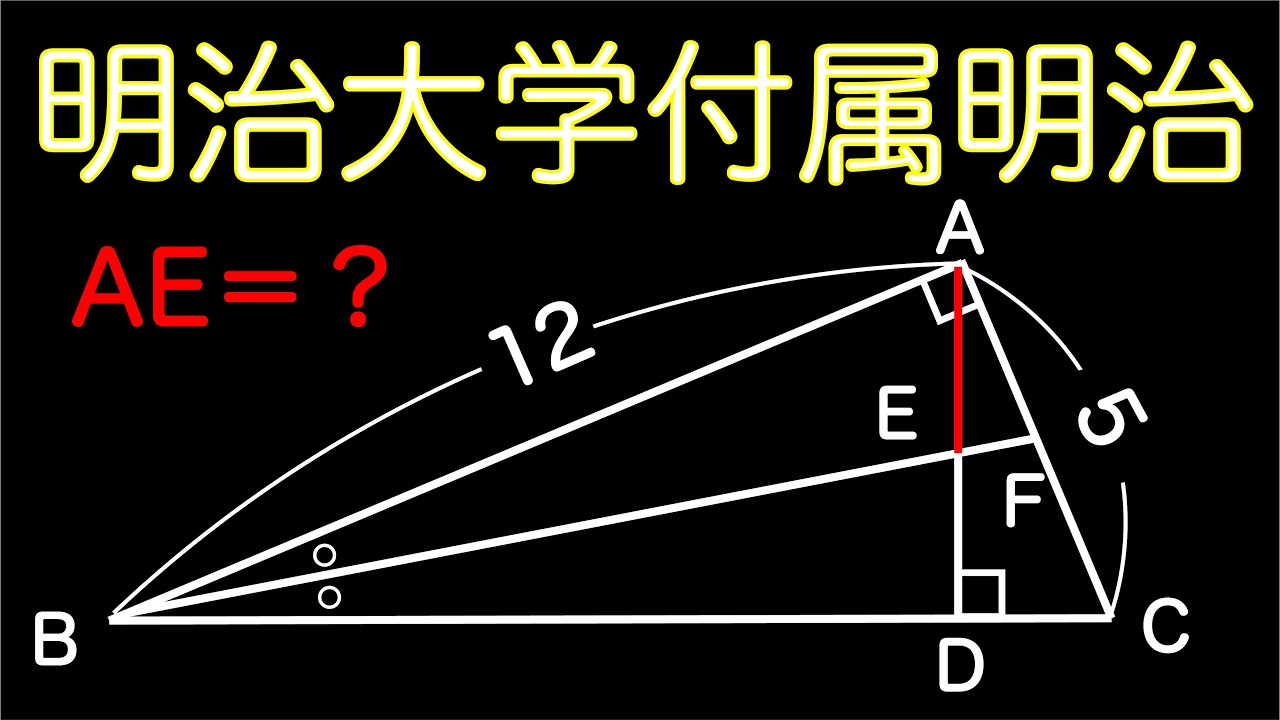
単元:
#数学(中学生)#高校入試過去問(数学)#明治大学付属明治高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
動画内の図を参照し、AEの長さを求めよ。
出典:2012年明治大学付属明治高等学校
この動画を見る
動画内の図を参照し、AEの長さを求めよ。
出典:2012年明治大学付属明治高等学校
