大阪星光学院高等学校
大阪星光学院高等学校
equation : Shirotan's cute kawaii math show #数学 #小学生テスト #高校入試 #高校受験
単元：
#数学(中学生)#中２数学#連立方程式#高校入試過去問(数学)#大阪星光学院高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
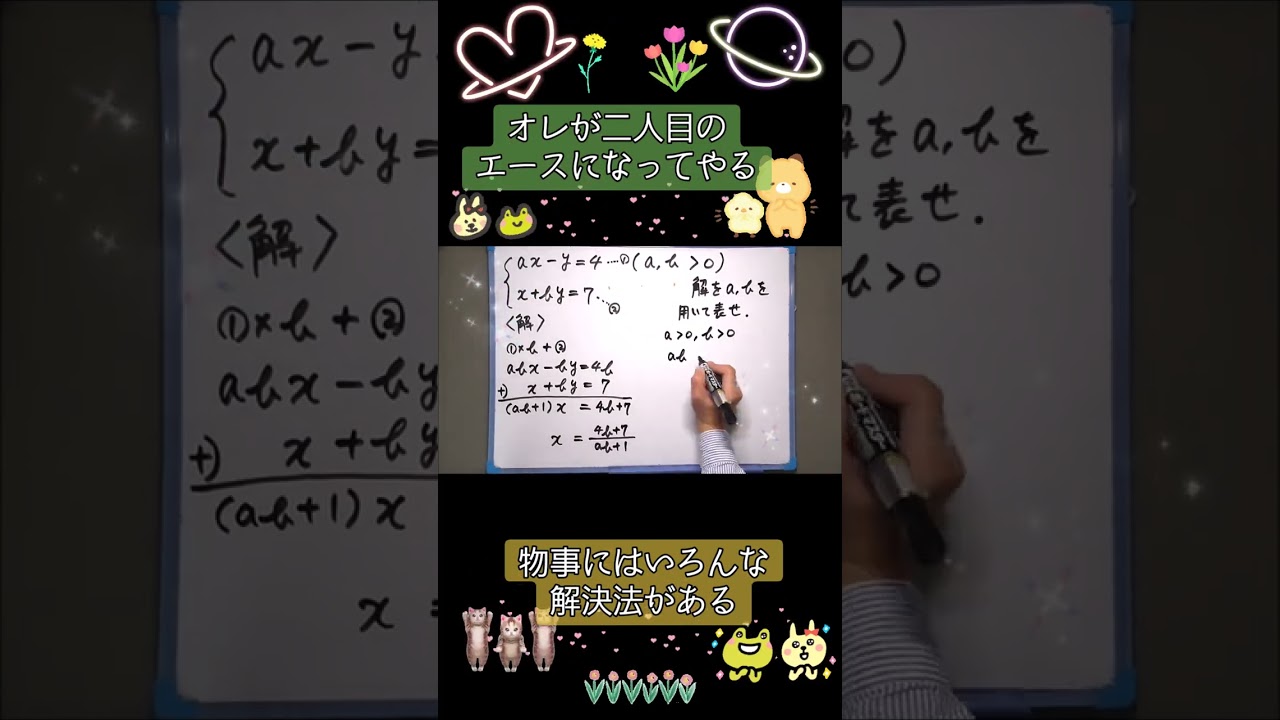
ax-y=4 (a,b,>0)
x+by=7
解をa,bを用いて表せ
この動画を見る
ax-y=4 (a,b,>0)
x+by=7
解をa,bを用いて表せ
【やることは分かるが…！】文字式：大阪星光学院高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)#大阪星光学院高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$x=1+\sqrt{2}+\sqrt{3}+\sqrt{5}$のとき、
$x^2-2x+5$の値を求めよ。
この動画を見る
$x=1+\sqrt{2}+\sqrt{3}+\sqrt{5}$のとき、
$x^2-2x+5$の値を求めよ。
【考えてみれば…！】整数：大阪星光学院高等学校～全国入試問題解法
単元：
#数学(中学生)#高校入試過去問(数学)#大阪星光学院高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ f(x):x $を3で割った余り(xは0以上の整数である)
$ f(1)+f(2)+f(3)+･･･+f(2023)=\Box $である.
大阪星光学院高等学校過去問
この動画を見る
$ f(x):x $を3で割った余り(xは0以上の整数である)
$ f(1)+f(2)+f(3)+･･･+f(2023)=\Box $である.
大阪星光学院高等学校過去問
【カッコの中には3つのルート！】平方根：大阪星光学院高等学校～全国入試問題解法
単元：
#数学(中学生)#中３数学#平方根#高校入試過去問(数学)#大阪星光学院高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
次の$ \Box $の中に$ \color{green}{正しい答え}$を入れなさい.
$ (\sqrt2+\sqrt3+\sqrt5)(\sqrt2+\sqrt3-\sqrt5)\times(\sqrt2-\sqrt3+\sqrt5)(-\sqrt2+\sqrt3+\sqrt5)=\Box $
大阪星光高校過去問
この動画を見る
次の$ \Box $の中に$ \color{green}{正しい答え}$を入れなさい.
$ (\sqrt2+\sqrt3+\sqrt5)(\sqrt2+\sqrt3-\sqrt5)\times(\sqrt2-\sqrt3+\sqrt5)(-\sqrt2+\sqrt3+\sqrt5)=\Box $
大阪星光高校過去問