 佐賀県立高校
佐賀県立高校
 佐賀県立高校
佐賀県立高校
佐賀県立高校入試2021年5⃣(4)「相似」
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2021年5⃣(4)「相似」
-----------------
動画内の図のように、ABを斜辺とする2つの直角三角形ABCとABDがあり、辺BCとADの交点をEとする。
また、AC=2cm、BC=3cm、CE=1cmとする。
点Eから辺ABに重線をひき、その交点をFとする。 このとき、(ア)、(イ)の問いに答えなさい。
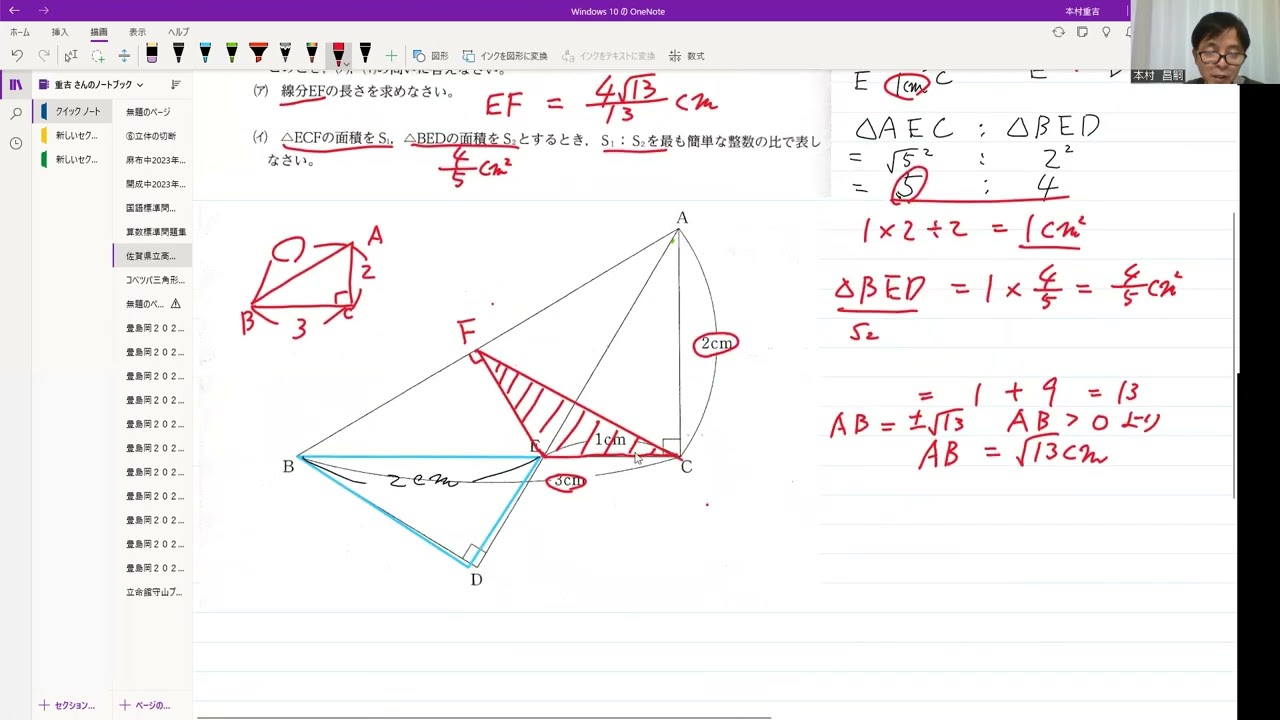
(ア)線分EFの長さを求めなさい。
(イ)△BCFの面積をS$_{1}$、△BEDの面積をS$_{2}$とするとき、S$_{1}$:S$_{2}$を
最も簡単な整数の比で表しなさい。
この動画を見る
佐賀県立高校入試2021年5⃣(4)「相似」
-----------------
動画内の図のように、ABを斜辺とする2つの直角三角形ABCとABDがあり、辺BCとADの交点をEとする。
また、AC=2cm、BC=3cm、CE=1cmとする。
点Eから辺ABに重線をひき、その交点をFとする。 このとき、(ア)、(イ)の問いに答えなさい。
(ア)線分EFの長さを求めなさい。
(イ)△BCFの面積をS$_{1}$、△BEDの面積をS$_{2}$とするとき、S$_{1}$:S$_{2}$を
最も簡単な整数の比で表しなさい。
佐賀県立高校入試2021年5⃣(1)~(3)「相似」
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2021年5⃣(1)~(3)「相似」
-----------------
動画内の図のように、ABを斜辺とする2つの直角三角形ABCとABDがあり、辺BCとADの交点をEとする。
また、AC=2cm、BC=3cm、CE=1cmとする。
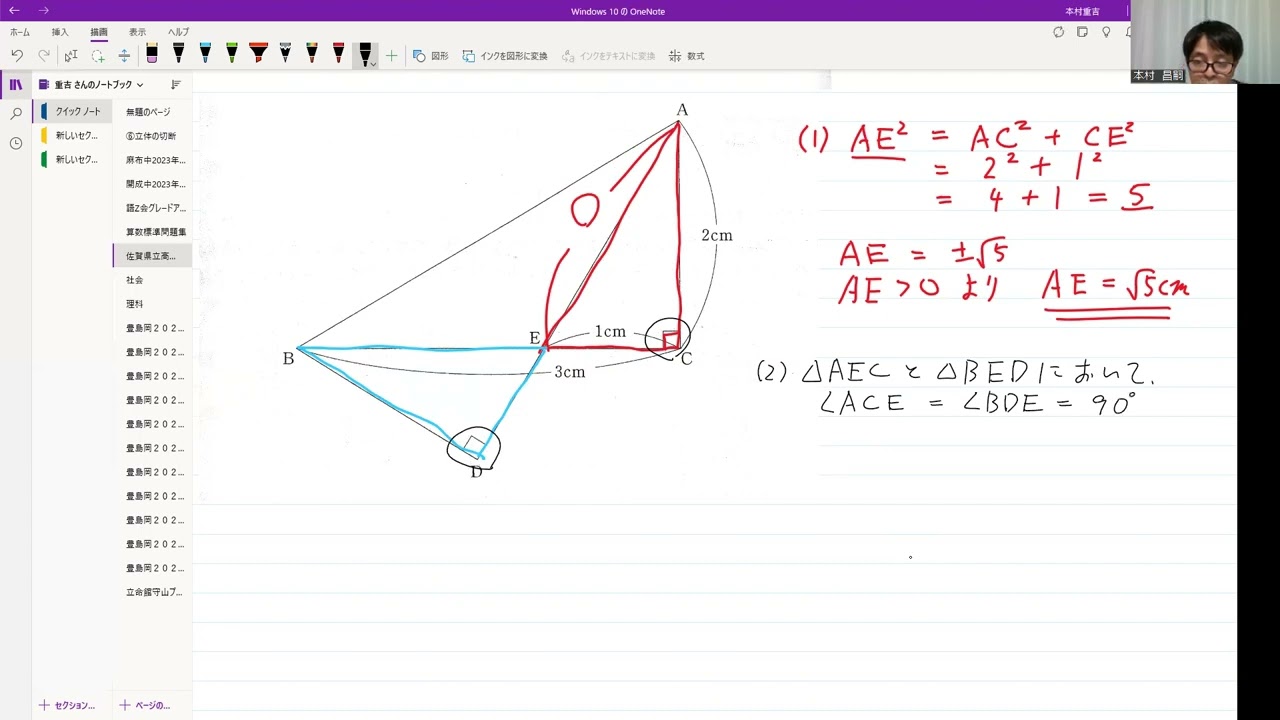
(1)線分AEの長さを求めなさい。
(2)△ABC$\sim$△BEDであることを証明しなさい。
(3)△ABEの面積を求めなさい。
この動画を見る
佐賀県立高校入試2021年5⃣(1)~(3)「相似」
-----------------
動画内の図のように、ABを斜辺とする2つの直角三角形ABCとABDがあり、辺BCとADの交点をEとする。
また、AC=2cm、BC=3cm、CE=1cmとする。
(1)線分AEの長さを求めなさい。
(2)△ABC$\sim$△BEDであることを証明しなさい。
(3)△ABEの面積を求めなさい。
佐賀県立高校入試2021年4⃣(5)「二次関数、一次関数」
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2021年4⃣(5)「二次関数、一次関数」
-----------------
動画内の図のように、関数 $y = ax^2$のグラフ上に3点A、B、Cがある。
点の座標は A(2, 2) 、点Bのx座標は-6、点Cのx座標は4である。
点Aを通りy軸に平行な直線と、2点B、Cを通る直線との交点をPとする。
また、点Pを通り△ABCの面積を2等分する直線と、2点A、Bを通る直線との交点をQとする。
このとき(ア)、(イ)の問いに答えなさい。
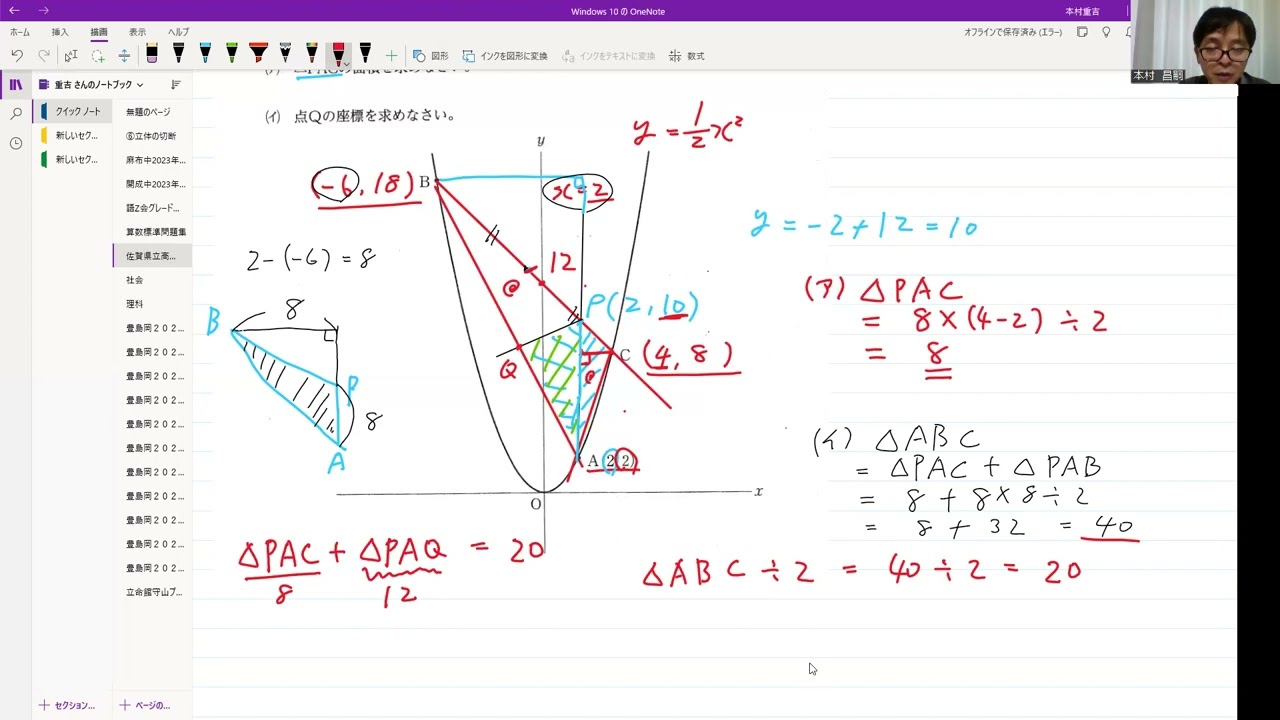
(ア) △PACの面積を求めなさい。
(イ) 点Qの座標を求めなさい。
この動画を見る
佐賀県立高校入試2021年4⃣(5)「二次関数、一次関数」
-----------------
動画内の図のように、関数 $y = ax^2$のグラフ上に3点A、B、Cがある。
点の座標は A(2, 2) 、点Bのx座標は-6、点Cのx座標は4である。
点Aを通りy軸に平行な直線と、2点B、Cを通る直線との交点をPとする。
また、点Pを通り△ABCの面積を2等分する直線と、2点A、Bを通る直線との交点をQとする。
このとき(ア)、(イ)の問いに答えなさい。
(ア) △PACの面積を求めなさい。
(イ) 点Qの座標を求めなさい。
賀県立高校入試2021年4⃣(1)~(4)「二次関数、一次関数」
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
賀県立高校入試2021年4⃣(1)~(4)「二次関数、一次関数」
-----------------
動画内の図のように、関数$y=ax^2$のグラフ上に3点A、B、Cがある。
点Aの座標はA(2.2)、点Bの$x$座標は-6、点Cの$x$座標は4である。
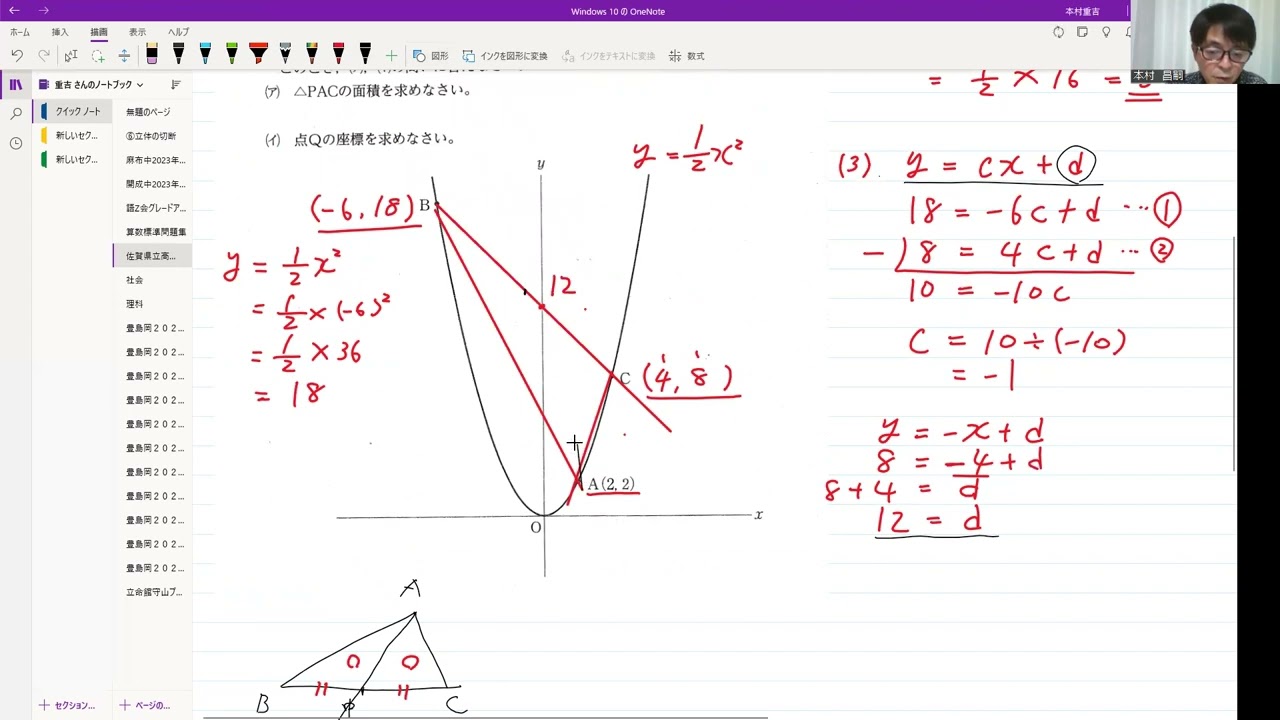
(1)aの値を求めなさい。
(2)点Cの$y$座標を求めなさい。
(3)2点B、Cを通る直線の切片を求めなさい。
(4)点Aを通り△ABCの面積を2等分する直線と、2点B、Cを通る直線との交点の座標を求めなさい。
この動画を見る
賀県立高校入試2021年4⃣(1)~(4)「二次関数、一次関数」
-----------------
動画内の図のように、関数$y=ax^2$のグラフ上に3点A、B、Cがある。
点Aの座標はA(2.2)、点Bの$x$座標は-6、点Cの$x$座標は4である。
(1)aの値を求めなさい。
(2)点Cの$y$座標を求めなさい。
(3)2点B、Cを通る直線の切片を求めなさい。
(4)点Aを通り△ABCの面積を2等分する直線と、2点B、Cを通る直線との交点の座標を求めなさい。
佐賀県立高校入試2021年「確率」
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2021年「確率」
-----------------
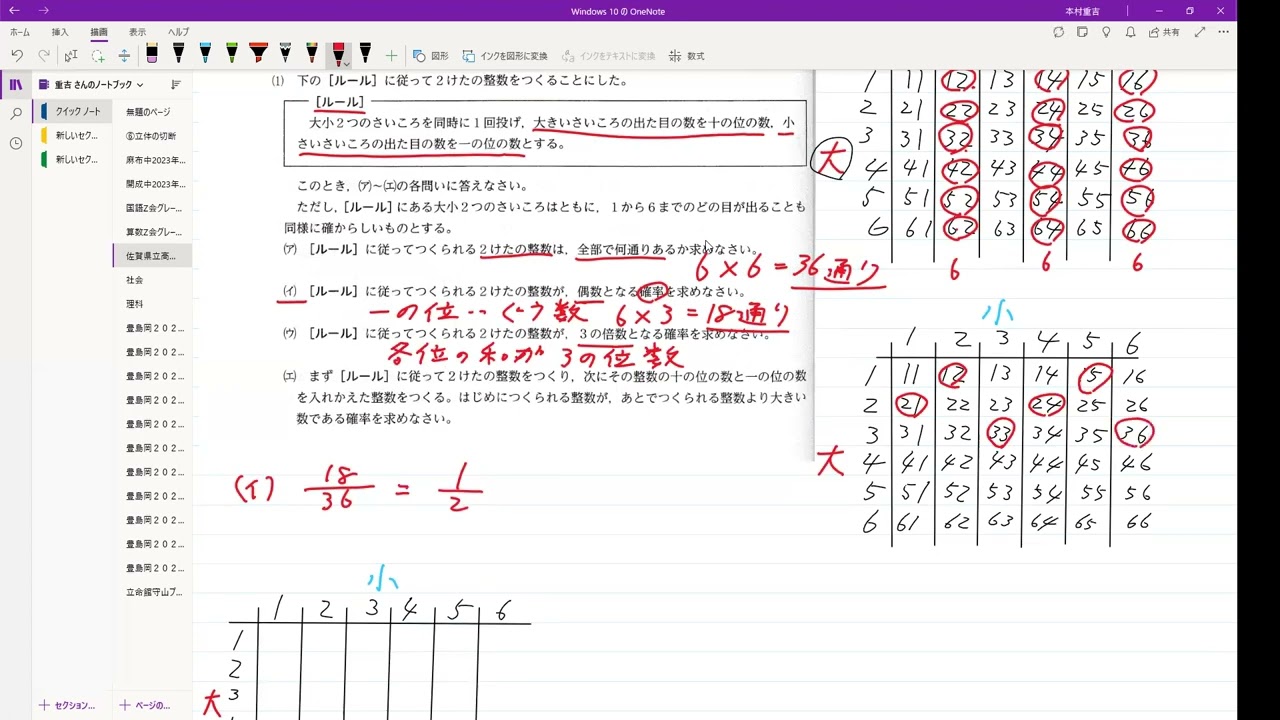
【ルール】
大小2つのさいころを同時に1回投げ、大きいさいころの出た目の数を十の位の数、小さいさいころの出た目の数を一の位の数としてけたの整数をつくる
このとき、下記の各問いに答えなさい。
ただし、(ルール)にある大小2つのさいころはともに、1から6までのどの目が出ることも同様に確からしいものとする。
(ア)【ルール】に従ってつくられる2けたの整数は、全部で何通りあるか求めなさい。
(イ)【ルール】に従ってつくられる2けたの整数が、偶数となる確率を求めなさい。
(ウ)【ルール】に従ってつくられる2けたの整数が、3の倍数となる確率を求めなさい。
(エ)まず【ルール】に従ってだけたの整数をつくり、次にその整数の十の位の数と一の位の数を入れかえた整数をつくる。
はじめにつくられる整数が、あとでつくられる整数より大きい数である確率を求めなさい。
この動画を見る
佐賀県立高校入試2021年「確率」
-----------------
【ルール】
大小2つのさいころを同時に1回投げ、大きいさいころの出た目の数を十の位の数、小さいさいころの出た目の数を一の位の数としてけたの整数をつくる
このとき、下記の各問いに答えなさい。
ただし、(ルール)にある大小2つのさいころはともに、1から6までのどの目が出ることも同様に確からしいものとする。
(ア)【ルール】に従ってつくられる2けたの整数は、全部で何通りあるか求めなさい。
(イ)【ルール】に従ってつくられる2けたの整数が、偶数となる確率を求めなさい。
(ウ)【ルール】に従ってつくられる2けたの整数が、3の倍数となる確率を求めなさい。
(エ)まず【ルール】に従ってだけたの整数をつくり、次にその整数の十の位の数と一の位の数を入れかえた整数をつくる。
はじめにつくられる整数が、あとでつくられる整数より大きい数である確率を求めなさい。
佐賀県立高校入試2021年「二次方程式」
単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2021年「二次方程式」
-----------------
三角形と長方形がある。
三角形は高さが底辺の長さの3倍であり、長方形は横の長さが縦の長さよりも2cm長い。
このとき、(ア)~(ウ)の各問いに答えなさい。
(ア)
長方形の縦の長さが$3cm$のとき、長方形の面積を求めなさい。
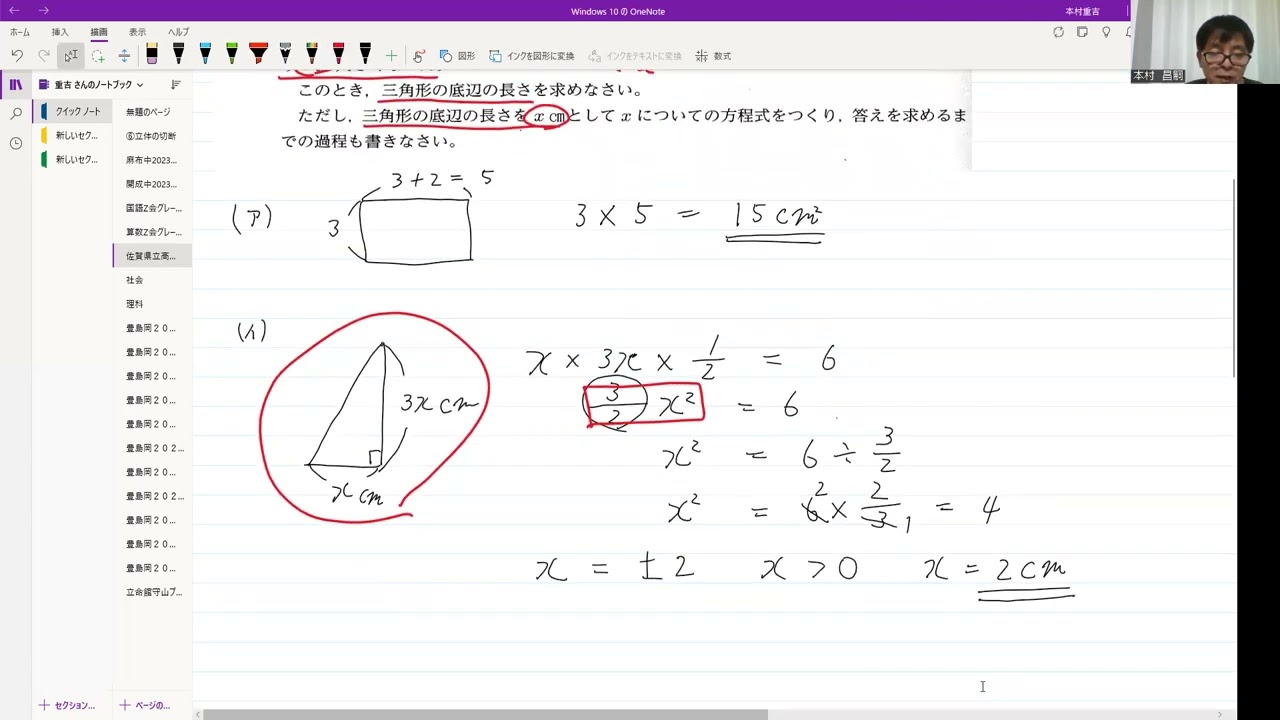
(イ)
三角形の面積が$6cm^2$とき、三角形の底辺の長さを求めなさい。
(ウ)
三角形の底辺の長さと、長方形の縦の長さが等しいとき、三角形の面積が長方形の面積より$6cm^2$回大きくなった。
このとき、三角形の底辺の長さを求めなさい。
ただし、三角形の底辺の長さを$xcm$として$x$についての方程式をつくり、答えを求めるまでの過程も書きなさい。
この動画を見る
佐賀県立高校入試2021年「二次方程式」
-----------------
三角形と長方形がある。
三角形は高さが底辺の長さの3倍であり、長方形は横の長さが縦の長さよりも2cm長い。
このとき、(ア)~(ウ)の各問いに答えなさい。
(ア)
長方形の縦の長さが$3cm$のとき、長方形の面積を求めなさい。
(イ)
三角形の面積が$6cm^2$とき、三角形の底辺の長さを求めなさい。
(ウ)
三角形の底辺の長さと、長方形の縦の長さが等しいとき、三角形の面積が長方形の面積より$6cm^2$回大きくなった。
このとき、三角形の底辺の長さを求めなさい。
ただし、三角形の底辺の長さを$xcm$として$x$についての方程式をつくり、答えを求めるまでの過程も書きなさい。
佐賀県立高校入試2021年2⃣連立方程式
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2021年2⃣連立方程式
-----------------
A中学校とB中学校の合計45人のバレーボール部員が、3日間の合同練習をすることになった。
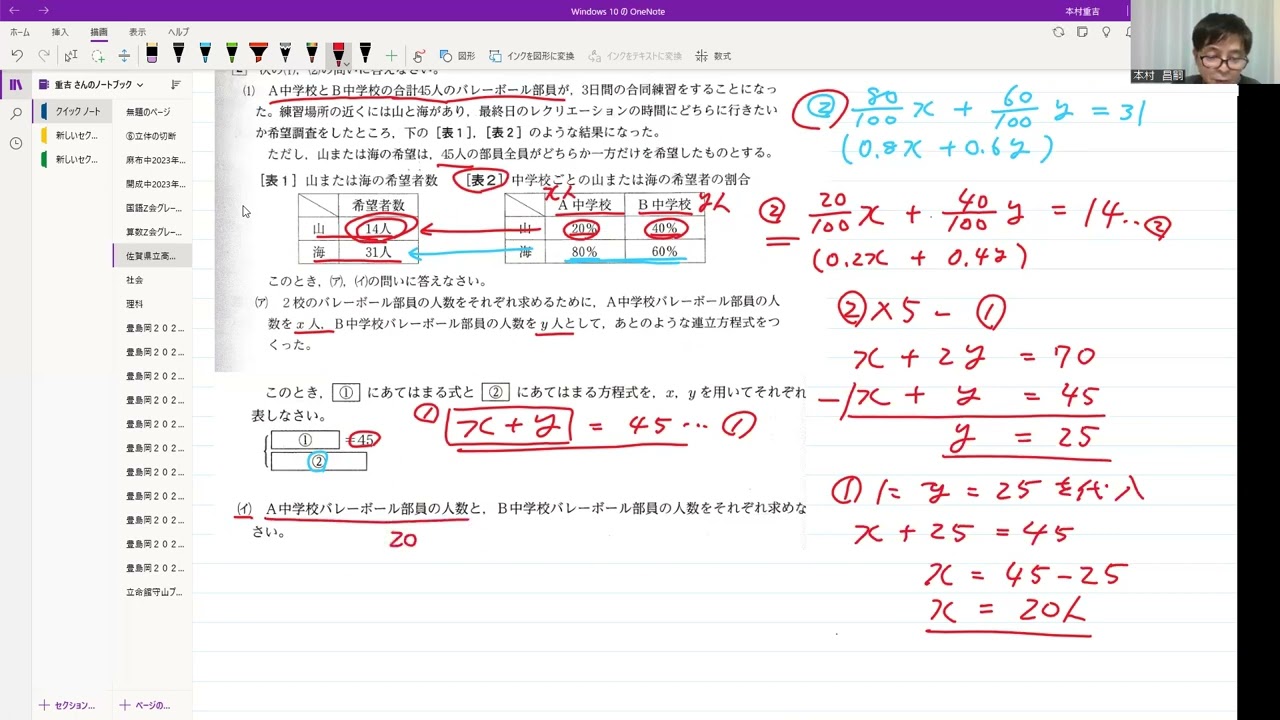
練習場所の近くには山と海があり、最終日のレクリエーションの時間にどちらに行きたいか希望調査をしたところ、動画内の表のような結果になった。
ただし、山または海の希望は、45人の部員全員がどちらか一方だけを希望したものとする。
(ア)
2校のバレーボール部員の人数をそれぞれ求めるために、A中学校バレーボール部員の人数を$x$人、B中学校バレーボール部員の人数を$y$人として、あとのような連立方程式をつくった。
このとき、①にあてはまる式と②にあてはまる方程式を、$x,y$を用いてそれぞれ表しなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
① = 45 \\
②
\end{array}
\right.
\end{eqnarray}$
(イ)
A中学校バレーボール部員の人数と、B中学校バレーボール部員の人数をそれぞれ求めなさい。
この動画を見る
佐賀県立高校入試2021年2⃣連立方程式
-----------------
A中学校とB中学校の合計45人のバレーボール部員が、3日間の合同練習をすることになった。
練習場所の近くには山と海があり、最終日のレクリエーションの時間にどちらに行きたいか希望調査をしたところ、動画内の表のような結果になった。
ただし、山または海の希望は、45人の部員全員がどちらか一方だけを希望したものとする。
(ア)
2校のバレーボール部員の人数をそれぞれ求めるために、A中学校バレーボール部員の人数を$x$人、B中学校バレーボール部員の人数を$y$人として、あとのような連立方程式をつくった。
このとき、①にあてはまる式と②にあてはまる方程式を、$x,y$を用いてそれぞれ表しなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
① = 45 \\
②
\end{array}
\right.
\end{eqnarray}$
(イ)
A中学校バレーボール部員の人数と、B中学校バレーボール部員の人数をそれぞれ求めなさい。
佐賀県立高校入試2022年5⃣相似(4)~(6)
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2022年5⃣相似(4)~(6)
-----------------
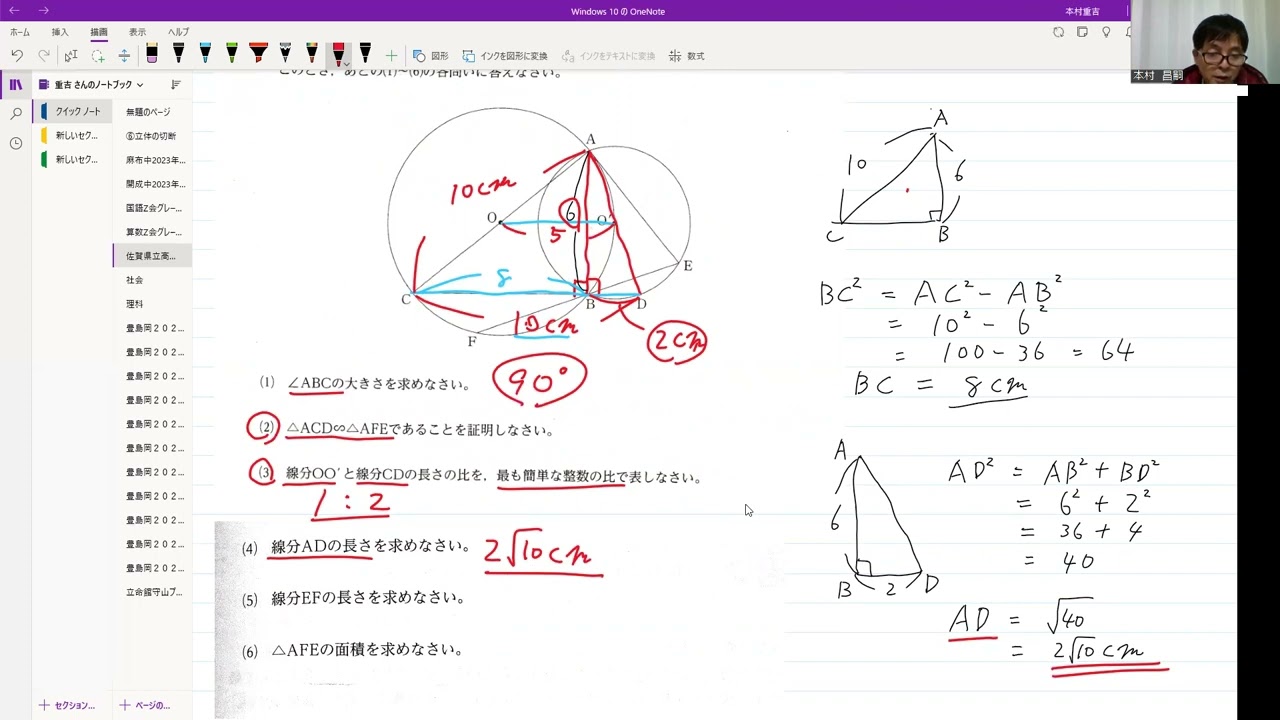
動画内の図のように、半径が5cmの円Oと、半径が円Oの半径よりも短い円O'があり、円O'の中心は円Oの周上にある。
2つの円の交点をA、Bとし、AB=6cmとする。
円Oの周上に線分ACが円Oの直径となるように点Cをとり、直線CBと円O'との交点のうち点Bと異なる点をDとする。
また、円O'の周上にAE=6cmとなるように点Eをとり、直線EBと円Oとの交点のうち点Bと異なる点をFとする。ただし、点Eは点Bと異なる点とする。
(4) 線分ADの長さを求めなさい。
(5) 線分EFの長さを求めなさい。
(6) △AFEの面積を求めなさい。
この動画を見る
佐賀県立高校入試2022年5⃣相似(4)~(6)
-----------------
動画内の図のように、半径が5cmの円Oと、半径が円Oの半径よりも短い円O'があり、円O'の中心は円Oの周上にある。
2つの円の交点をA、Bとし、AB=6cmとする。
円Oの周上に線分ACが円Oの直径となるように点Cをとり、直線CBと円O'との交点のうち点Bと異なる点をDとする。
また、円O'の周上にAE=6cmとなるように点Eをとり、直線EBと円Oとの交点のうち点Bと異なる点をFとする。ただし、点Eは点Bと異なる点とする。
(4) 線分ADの長さを求めなさい。
(5) 線分EFの長さを求めなさい。
(6) △AFEの面積を求めなさい。
佐賀県立高校入試2022年5⃣相似(1)~(3)
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2022年5⃣相似(1)~(3)
-----------------
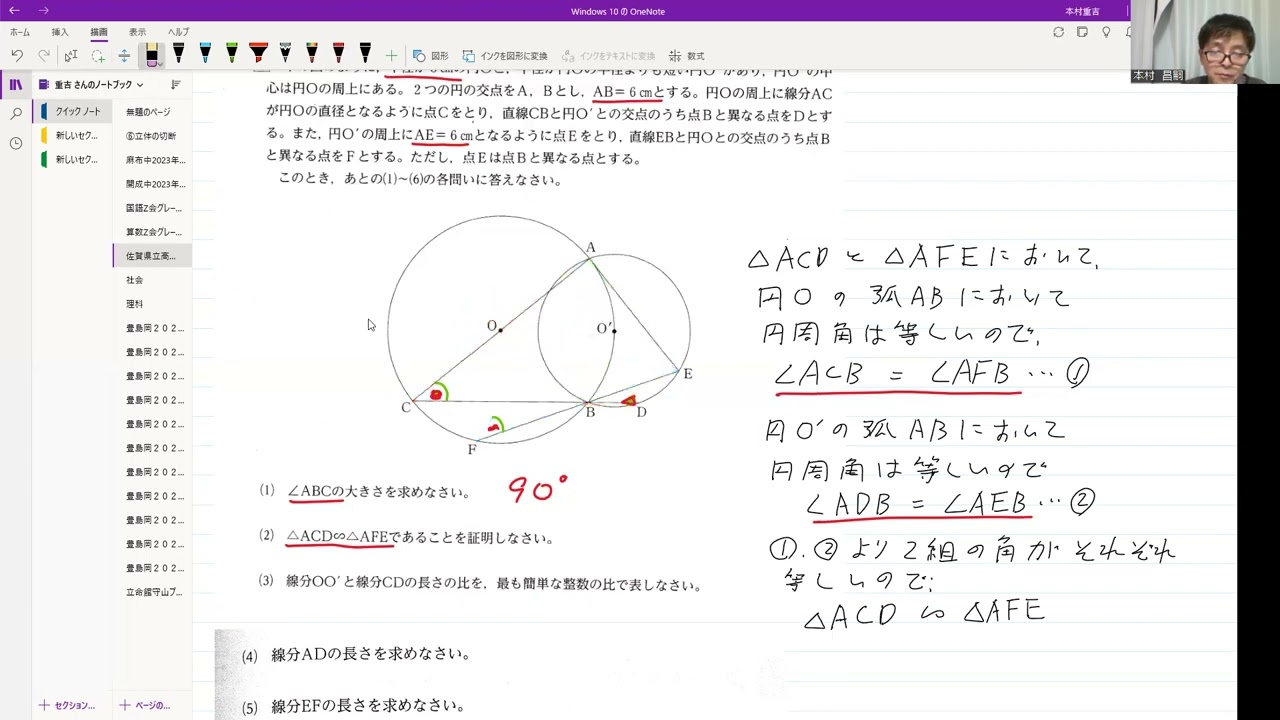
動画内の図のように、半径が5cmの円Oと、半径が円Oの半径よりも短い円O'があり、円O'の中心は円Oの周上にある。
2つの円の交点をA、Bとし、AB=6cmとする。
円Oの周上に線分ACが円Oの直径となるように点Cをとり、直線CBと円O'との交点のうち点Bと異なる点をDとする。
また、円O'の周上にAE=6cmとなるように点Eをとり、直線EBと円Oとの交点のうち点Bと異なる点をFとする。ただし、点Eは点Bと異なる点とする。
(1) ∠ABCの大きさを求めなさい。
(2) △ACD$\backsim$△AFEであることを証明しなさい。
(3) 線分OO'と線分CDの長さの比を、最も簡単な整数の比で表しなさい。
この動画を見る
佐賀県立高校入試2022年5⃣相似(1)~(3)
-----------------
動画内の図のように、半径が5cmの円Oと、半径が円Oの半径よりも短い円O'があり、円O'の中心は円Oの周上にある。
2つの円の交点をA、Bとし、AB=6cmとする。
円Oの周上に線分ACが円Oの直径となるように点Cをとり、直線CBと円O'との交点のうち点Bと異なる点をDとする。
また、円O'の周上にAE=6cmとなるように点Eをとり、直線EBと円Oとの交点のうち点Bと異なる点をFとする。ただし、点Eは点Bと異なる点とする。
(1) ∠ABCの大きさを求めなさい。
(2) △ACD$\backsim$△AFEであることを証明しなさい。
(3) 線分OO'と線分CDの長さの比を、最も簡単な整数の比で表しなさい。
佐賀県立高校入試2022年4⃣関数(5)
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2022年4⃣関数(5)
-----------------
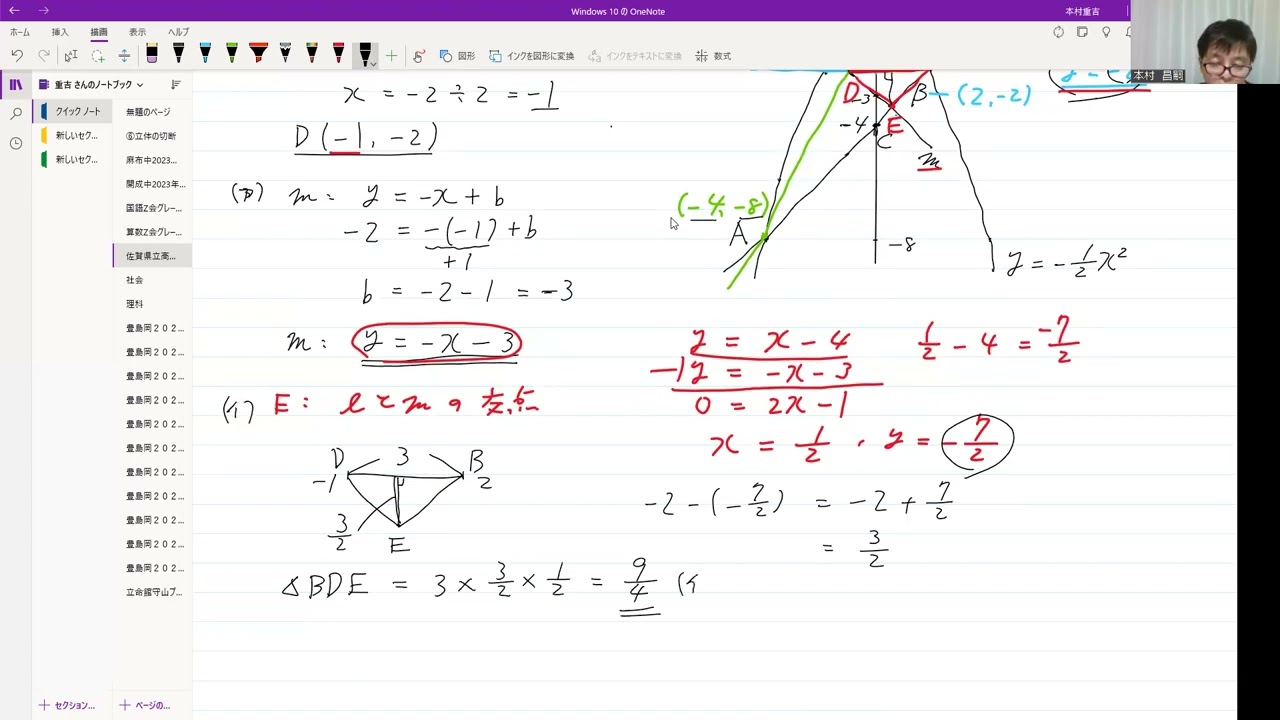
点Bを通り$x$軸に平行な直線と、原点と点Aを通る直線との交点をDとする。
また、点Dを通り、傾き-1の直線を$m$とし、直線$l$と直線$m$との交点をEとする。
このとき、(ア)~(ウ)の各問いに答えなさい。
(ア)直線$m$の式を求めなさい。
(イ)△BDEの面積を求めなさい。
(ウ)△ACDの面積を$S$.△BDEの面積を$T$とするとき、$S:T$を最も簡単な整数の比で表しなさい。
この動画を見る
佐賀県立高校入試2022年4⃣関数(5)
-----------------
点Bを通り$x$軸に平行な直線と、原点と点Aを通る直線との交点をDとする。
また、点Dを通り、傾き-1の直線を$m$とし、直線$l$と直線$m$との交点をEとする。
このとき、(ア)~(ウ)の各問いに答えなさい。
(ア)直線$m$の式を求めなさい。
(イ)△BDEの面積を求めなさい。
(ウ)△ACDの面積を$S$.△BDEの面積を$T$とするとき、$S:T$を最も簡単な整数の比で表しなさい。
佐賀県立高校入試2022年④関数(1)~(4)
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2022年④関数(1)~(4)
-----------------
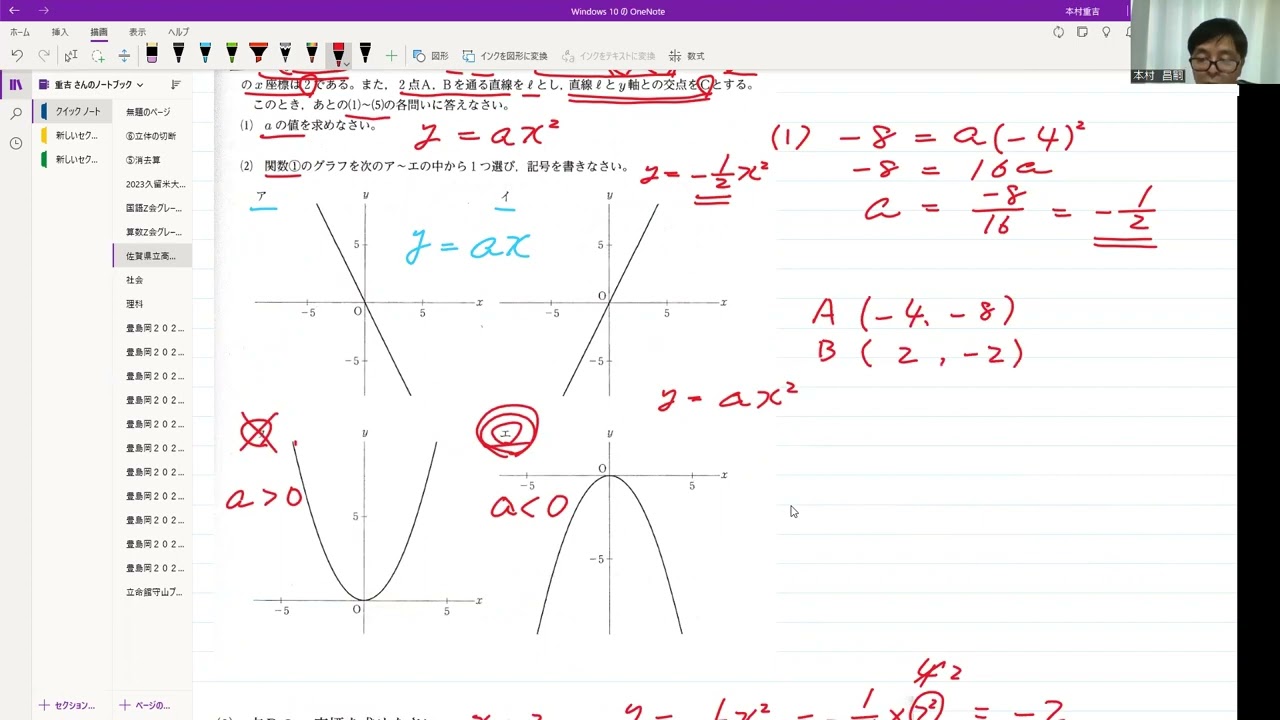
関数$y=ax^2$・・・①のグラフ上に2点A、Bがある。
点Aの座標は(-4.-8)であり、点Bの$x$座標は2である。
また、2点A、Bを通る直線を$l$とし、直線$l$と$y$軸との交点をCとする。
(1)aの値を求めなさい。
(2)関数①のグラフを動画内のア~エの中から1つ選び、記号を書きなさい。
(3) 点Bの$y$座標を求めなさい。
(4) 点Cの座標を求めなさい。
この動画を見る
佐賀県立高校入試2022年④関数(1)~(4)
-----------------
関数$y=ax^2$・・・①のグラフ上に2点A、Bがある。
点Aの座標は(-4.-8)であり、点Bの$x$座標は2である。
また、2点A、Bを通る直線を$l$とし、直線$l$と$y$軸との交点をCとする。
(1)aの値を求めなさい。
(2)関数①のグラフを動画内のア~エの中から1つ選び、記号を書きなさい。
(3) 点Bの$y$座標を求めなさい。
(4) 点Cの座標を求めなさい。
佐賀県立高校入試3⃣公約数
単元:
#数学(中学生)#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試3⃣公約数
-----------------
(ア)
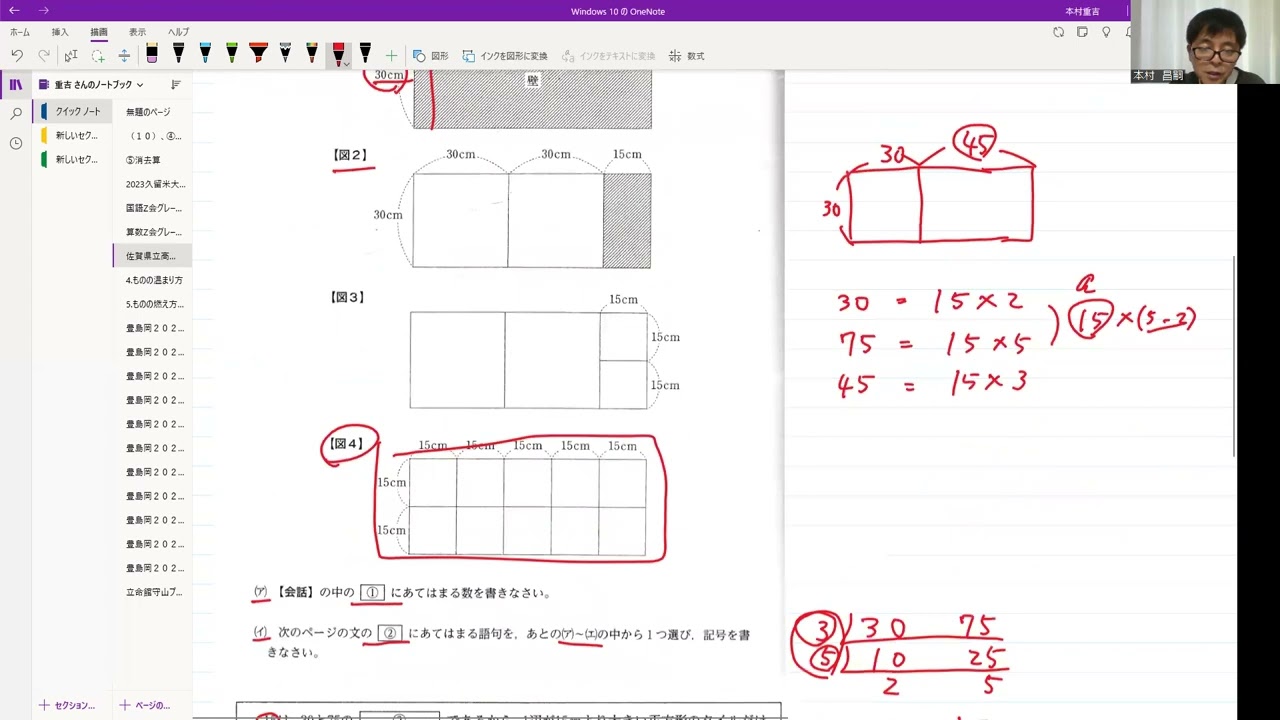
【会話】の中の① にあてはまる数を書きなさい。
(イ)
次のページの文の②にあてはまる語句を、あとの㋐~㋓の中から1つ選び、記号を書きなさい。
-----------------
15は、30と75の②であるから、1辺が15cmより大きい正方形のタイルだけを使って、縦の長さが30cm、横の長さが75cmの長方形の壁にタイルをすき間なく貼ることはできない。
-----------------
㋐最小公倍数
㋑自然数
㋒最大公約数
㋓素数
(ウ)
縦の長さ319g、横の長さが377cmの長方形の壁に、同じ大きさの正方形のタイルを、最も少ない枚数ですき間なく貼りたい。
このとき、使用するタイルの1辺の長さを求めなさい。
この動画を見る
佐賀県立高校入試3⃣公約数
-----------------
(ア)
【会話】の中の① にあてはまる数を書きなさい。
(イ)
次のページの文の②にあてはまる語句を、あとの㋐~㋓の中から1つ選び、記号を書きなさい。
-----------------
15は、30と75の②であるから、1辺が15cmより大きい正方形のタイルだけを使って、縦の長さが30cm、横の長さが75cmの長方形の壁にタイルをすき間なく貼ることはできない。
-----------------
㋐最小公倍数
㋑自然数
㋒最大公約数
㋓素数
(ウ)
縦の長さ319g、横の長さが377cmの長方形の壁に、同じ大きさの正方形のタイルを、最も少ない枚数ですき間なく貼りたい。
このとき、使用するタイルの1辺の長さを求めなさい。
佐賀県立高校入試2022年数学2⃣連立方程式
単元:
#数学(中学生)#中2数学#連立方程式#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2022年数学2⃣連立方程式
-----------------
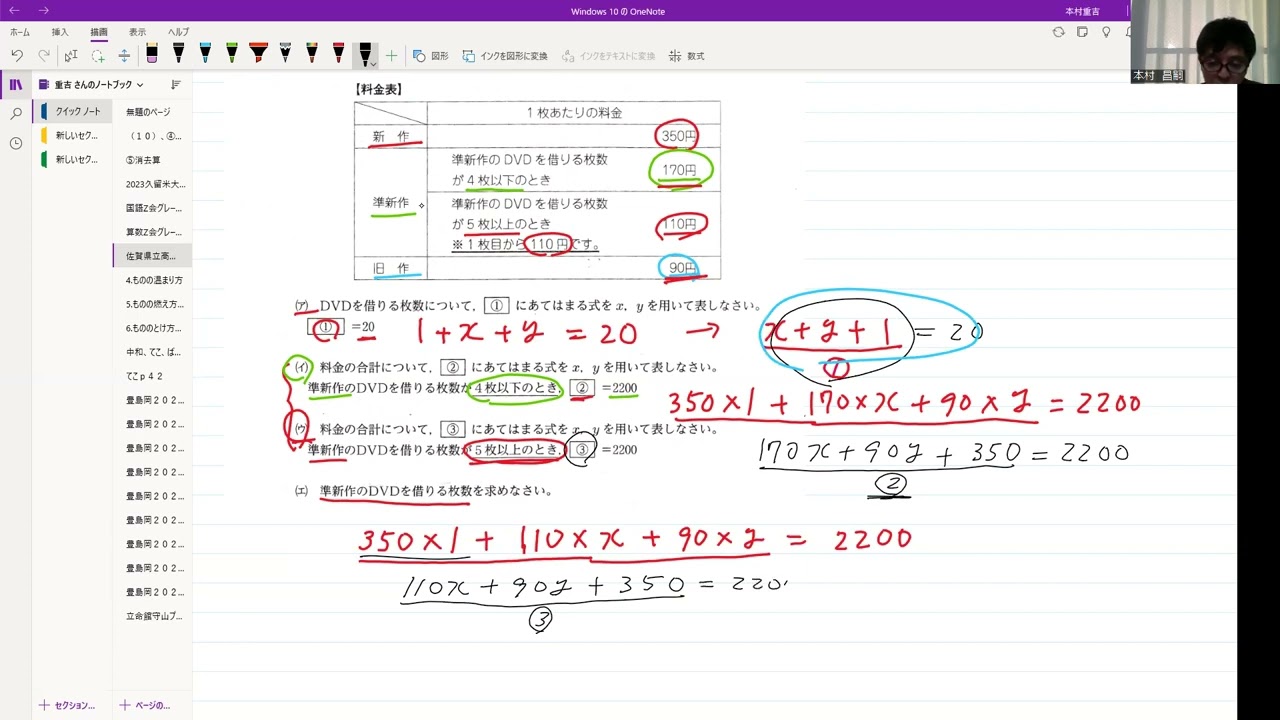
(ア)
DVDを借りる枚数について、①にあてはまる式を$x$、$y$を用いて表しなさい。
①=20
(イ)
料金の合計について、②にあてはまる式を$x$、$y$を用いて表しなさい。
準新作のDVDを借りる枚数が4枚以下のとき、②=2200
(ウ)
料金の合計について、③にあてはまる式を$x$、$y$を用いて表しなさい。
準新作のDVDを借りる枚数が5枚以上のとき。③=2200
(エ)
準新作のDVDを借りる枚数を求めなさい。
この動画を見る
佐賀県立高校入試2022年数学2⃣連立方程式
-----------------
(ア)
DVDを借りる枚数について、①にあてはまる式を$x$、$y$を用いて表しなさい。
①=20
(イ)
料金の合計について、②にあてはまる式を$x$、$y$を用いて表しなさい。
準新作のDVDを借りる枚数が4枚以下のとき、②=2200
(ウ)
料金の合計について、③にあてはまる式を$x$、$y$を用いて表しなさい。
準新作のDVDを借りる枚数が5枚以上のとき。③=2200
(エ)
準新作のDVDを借りる枚数を求めなさい。
佐賀県立高校入試2022年数学2⃣二次方程式
単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2022年数学2⃣二次方程式
-----------------
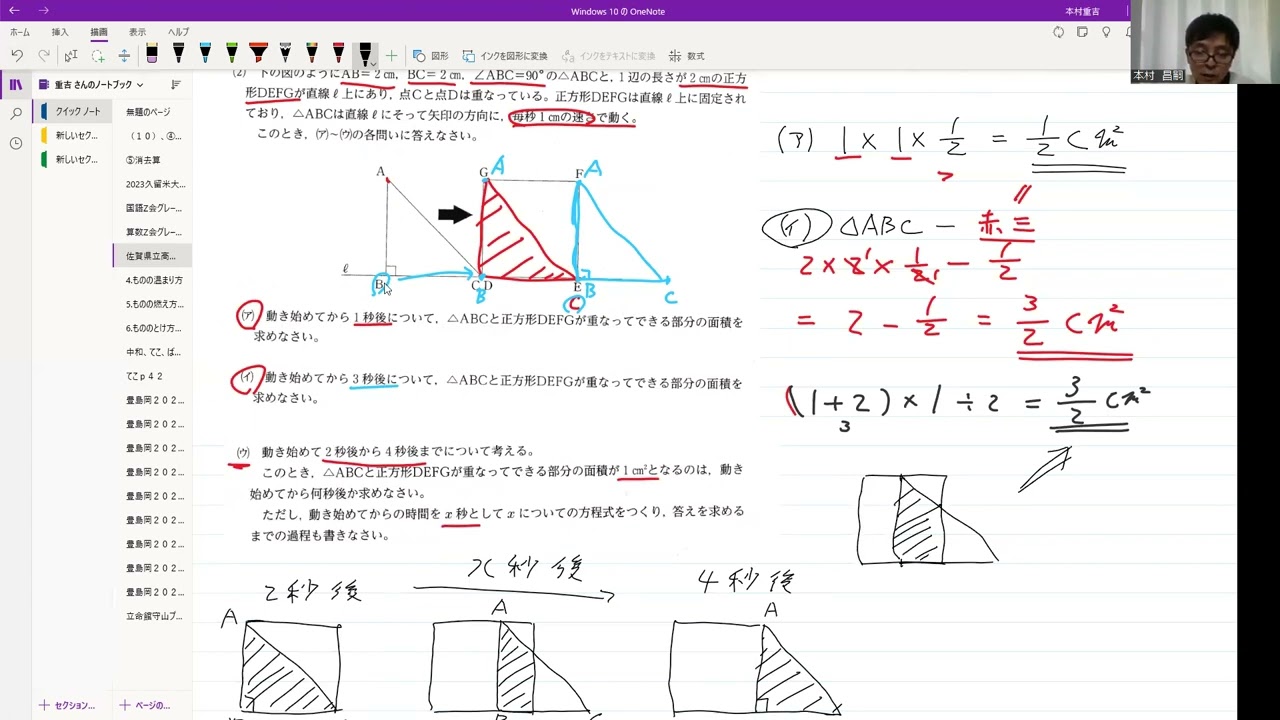
(ア)
動き始めてから1秒後について、△ABCと正方形DEFGが重なってできる部分の面積を求めなさい。
(イ)
動き始めてから3秒後について、△ABCと正方形DEFGが重なってできる部分の面積を求めなさい。
(ウ)
動き始めて2秒後から4秒後までについて考える。
このとき、△ABCと正方形DEFGが重なってできる部分の面積が1cm²となるのは、動き始めてから何秒後か求めなさい。
ただし、動き始めてからの時間を$x$秒として$x$についての方程式をつくり、答えを求めるまでの過程も書きなさい。
この動画を見る
佐賀県立高校入試2022年数学2⃣二次方程式
-----------------
(ア)
動き始めてから1秒後について、△ABCと正方形DEFGが重なってできる部分の面積を求めなさい。
(イ)
動き始めてから3秒後について、△ABCと正方形DEFGが重なってできる部分の面積を求めなさい。
(ウ)
動き始めて2秒後から4秒後までについて考える。
このとき、△ABCと正方形DEFGが重なってできる部分の面積が1cm²となるのは、動き始めてから何秒後か求めなさい。
ただし、動き始めてからの時間を$x$秒として$x$についての方程式をつくり、答えを求めるまでの過程も書きなさい。
佐賀県立高校入試2022年数学3⃣確率
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2022年数学3⃣確率
-----------------
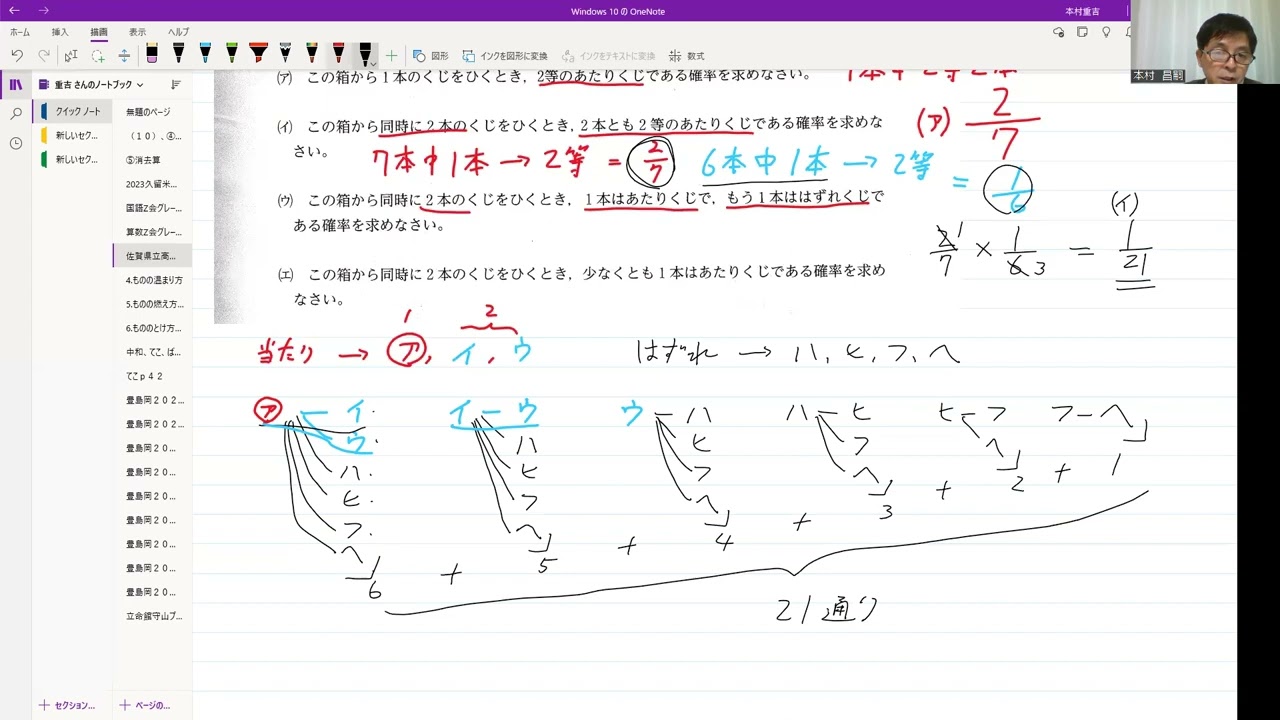
(ア)
この箱から1本のくじをひくとき、2等のあたりくじである確率を求めなさい。
(イ)
この箱から同時に2本のくじをひくとき、2本とも2等のあたりくじである確率を求めなさい。
(ウ)
この箱から同時に2本のくじをひくとき、1本はあたりくじで、もう1本ははずれくじである確率を求めなさい。
(エ)
この箱から同時に2本のくじをひくとき、少なくとも1本はあたりくじである確率を求めなさい。
この動画を見る
佐賀県立高校入試2022年数学3⃣確率
-----------------
(ア)
この箱から1本のくじをひくとき、2等のあたりくじである確率を求めなさい。
(イ)
この箱から同時に2本のくじをひくとき、2本とも2等のあたりくじである確率を求めなさい。
(ウ)
この箱から同時に2本のくじをひくとき、1本はあたりくじで、もう1本ははずれくじである確率を求めなさい。
(エ)
この箱から同時に2本のくじをひくとき、少なくとも1本はあたりくじである確率を求めなさい。
【3分で数学の知識が1 up!】図形:佐賀県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#空間図形#平面図形#高校入試過去問(数学)#佐賀県立高校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
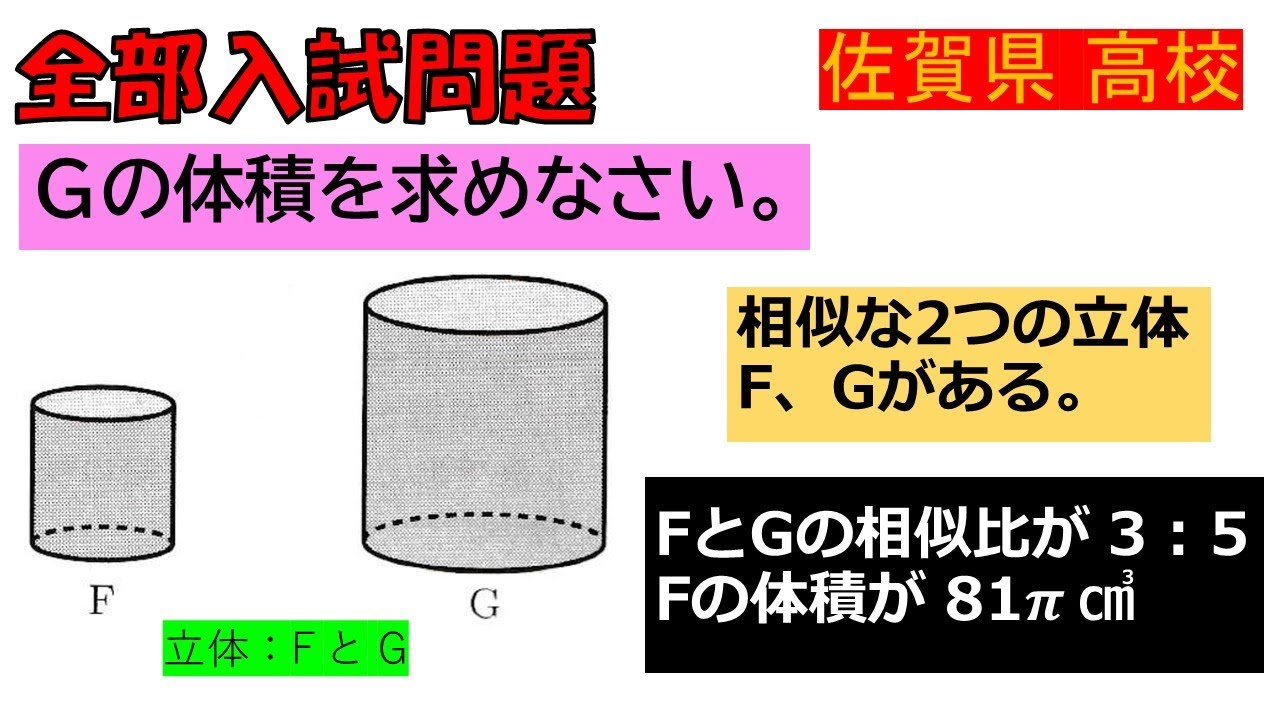
入試問題 佐賀県の公立高校
$G$の体積を求めなさい。
相似な2つの立体 $F$、$G$がある。
$F$と$G$の相似比が$3:5$
Fの体積が $81πcm^3$
※図は動画内参照
この動画を見る
入試問題 佐賀県の公立高校
$G$の体積を求めなさい。
相似な2つの立体 $F$、$G$がある。
$F$と$G$の相似比が$3:5$
Fの体積が $81πcm^3$
※図は動画内参照
【順を追って、理解深まる!】一次関数:佐賀県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#佐賀県立高校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 佐賀県の公立高等学校
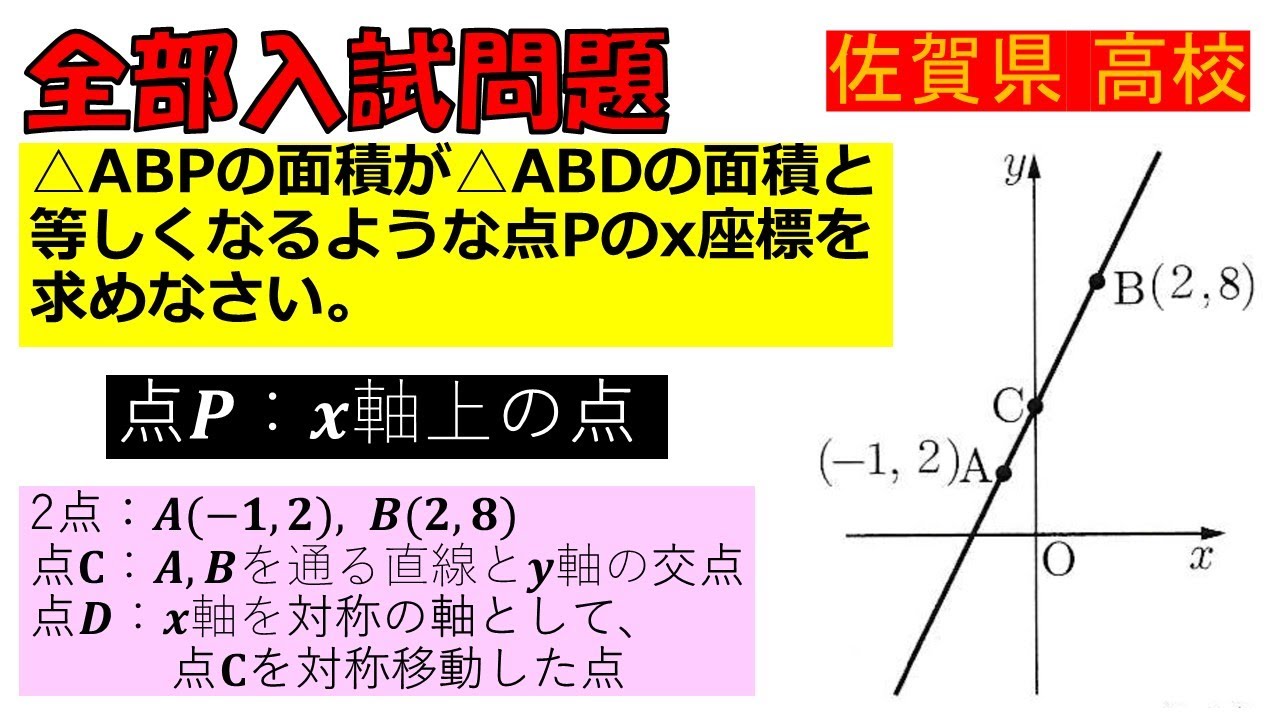
$\triangle ABP$の面積が$\triangle ABD$の面積と
等しくなるような点Pのx座標を 求めなさい。
点P:x軸上の点
2点:A(-1,2), B(2,8)
点C: A, Bを通る直線と軸の交点
点D:x軸を対称の軸として、
点Cを対称移動した点
※図は動画内参照
この動画を見る
入試問題 佐賀県の公立高等学校
$\triangle ABP$の面積が$\triangle ABD$の面積と
等しくなるような点Pのx座標を 求めなさい。
点P:x軸上の点
2点:A(-1,2), B(2,8)
点C: A, Bを通る直線と軸の交点
点D:x軸を対称の軸として、
点Cを対称移動した点
※図は動画内参照
