 東京都立日比谷高等学校
東京都立日比谷高等学校
 東京都立日比谷高等学校
東京都立日比谷高等学校
【解法は一瞬迷うところ…!】二次方程式:東京都立日比谷高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#東京都立日比谷高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$(x-1)^2-4(x-2)^2=0$を解け。
この動画を見る
$(x-1)^2-4(x-2)^2=0$を解け。
【完答するために…!】二次方程式:東京都立日比谷高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#東京都立日比谷高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x^2-5x+6=0 $の2つの解の和が
$ x^2-2ax+a^2-1=0 $の解の1つになっているとき,$ a$の値を全て求めよ.
都立日比谷高校過去問
この動画を見る
$ x^2-5x+6=0 $の2つの解の和が
$ x^2-2ax+a^2-1=0 $の解の1つになっているとき,$ a$の値を全て求めよ.
都立日比谷高校過去問
因数分解:東京都立日比谷高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#東京都立日比谷高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立日比谷高等学校
$\displaystyle \frac{(2x-6)^2}{4}-5x+15$
を因数分解せよ。
この動画を見る
入試問題 東京都立日比谷高等学校
$\displaystyle \frac{(2x-6)^2}{4}-5x+15$
を因数分解せよ。
平方根:日比谷高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#東京都立日比谷高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 日比谷高等学校
次の各問に答えよ。
$(\displaystyle \frac{\sqrt{ 7 }-\sqrt{ 12 }}{2})(\displaystyle \frac{\sqrt{ 7 }}{2}+\sqrt{ 3 })+\sqrt{ 18 }$
を計算せよ。
この動画を見る
入試問題 日比谷高等学校
次の各問に答えよ。
$(\displaystyle \frac{\sqrt{ 7 }-\sqrt{ 12 }}{2})(\displaystyle \frac{\sqrt{ 7 }}{2}+\sqrt{ 3 })+\sqrt{ 18 }$
を計算せよ。
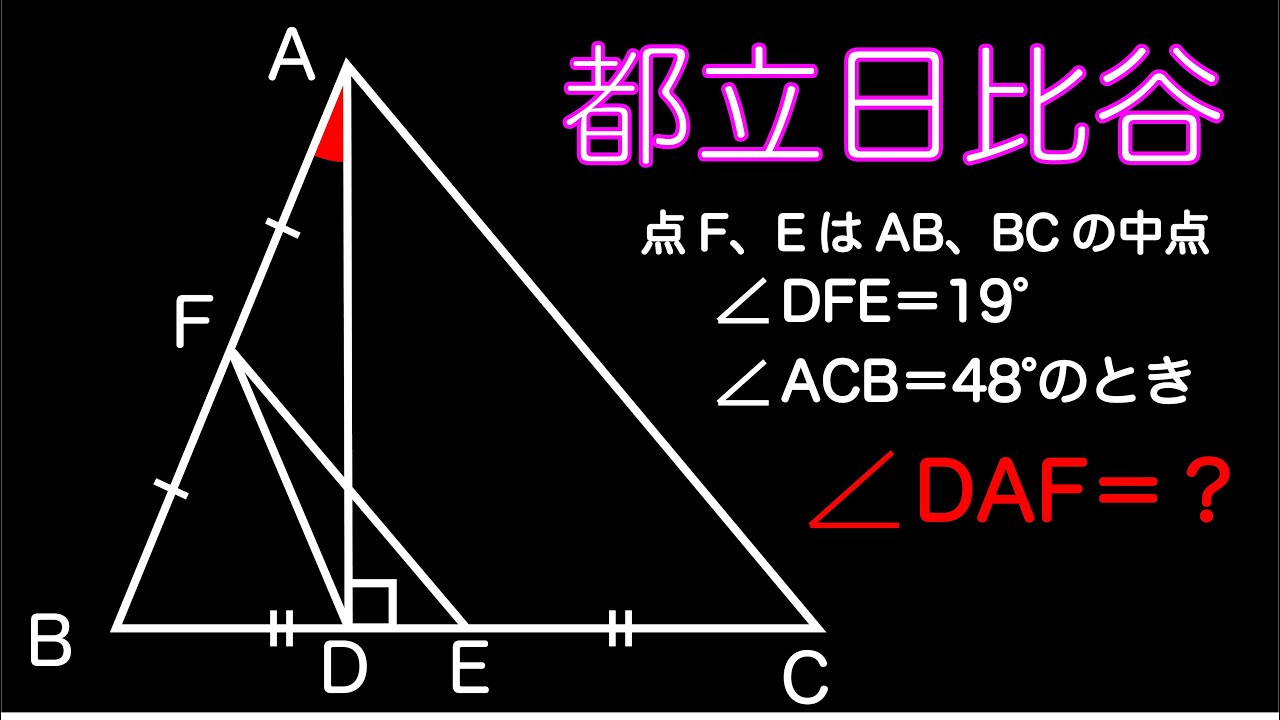
日比谷高校の角度を求める問題!!
単元:
#数学(中学生)#高校入試過去問(数学)#東京都立日比谷高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
点$F,E$は$AB,BC$の中点
$\angle DFE=19^{ \circ }$
$\angle ACB=48^{ \circ }$のとき
$\angle DAF=??$
出典:東京都立日比谷高等学校
この動画を見る
点$F,E$は$AB,BC$の中点
$\angle DFE=19^{ \circ }$
$\angle ACB=48^{ \circ }$のとき
$\angle DAF=??$
出典:東京都立日比谷高等学校
日比谷高校の計算問題(2003)

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#東京都立日比谷高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
$(\displaystyle \frac{\sqrt{ 6 }+\sqrt{ 5 }}{\sqrt{ 2 }})^2-(\sqrt{ 6 }+\sqrt{ 5 })(\sqrt{ 6 }-\sqrt{ 5 })+(\displaystyle \frac{\sqrt{ 6 }-\sqrt{ 5 }}{\sqrt{ 2 }})^2$
出典:2003年東京都立日比谷高等学校
この動画を見る
$(\displaystyle \frac{\sqrt{ 6 }+\sqrt{ 5 }}{\sqrt{ 2 }})^2-(\sqrt{ 6 }+\sqrt{ 5 })(\sqrt{ 6 }-\sqrt{ 5 })+(\displaystyle \frac{\sqrt{ 6 }-\sqrt{ 5 }}{\sqrt{ 2 }})^2$
出典:2003年東京都立日比谷高等学校
2019日比谷高校数学の最初の2問!!(高校入試数学)

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#高校入試過去問(数学)#東京都立日比谷高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
問1
$(3-\displaystyle \frac{1}{\sqrt{ 3 }})^2+\displaystyle \frac{(\sqrt{ 6 }-\sqrt{ 2 })(3+-\sqrt{ 3 })}{\sqrt{ 2 }}$
問2
$(6-x)^2+9(x-6)-90$を因数分解せよ
出典:2019年東京都立日比谷高等学校 高校入試
この動画を見る
問1
$(3-\displaystyle \frac{1}{\sqrt{ 3 }})^2+\displaystyle \frac{(\sqrt{ 6 }-\sqrt{ 2 })(3+-\sqrt{ 3 })}{\sqrt{ 2 }}$
問2
$(6-x)^2+9(x-6)-90$を因数分解せよ
出典:2019年東京都立日比谷高等学校 高校入試
