 空間図形
空間図形
 空間図形
空間図形
【手早く工夫して…!】空間図形:名古屋女子大学高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#空間図形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
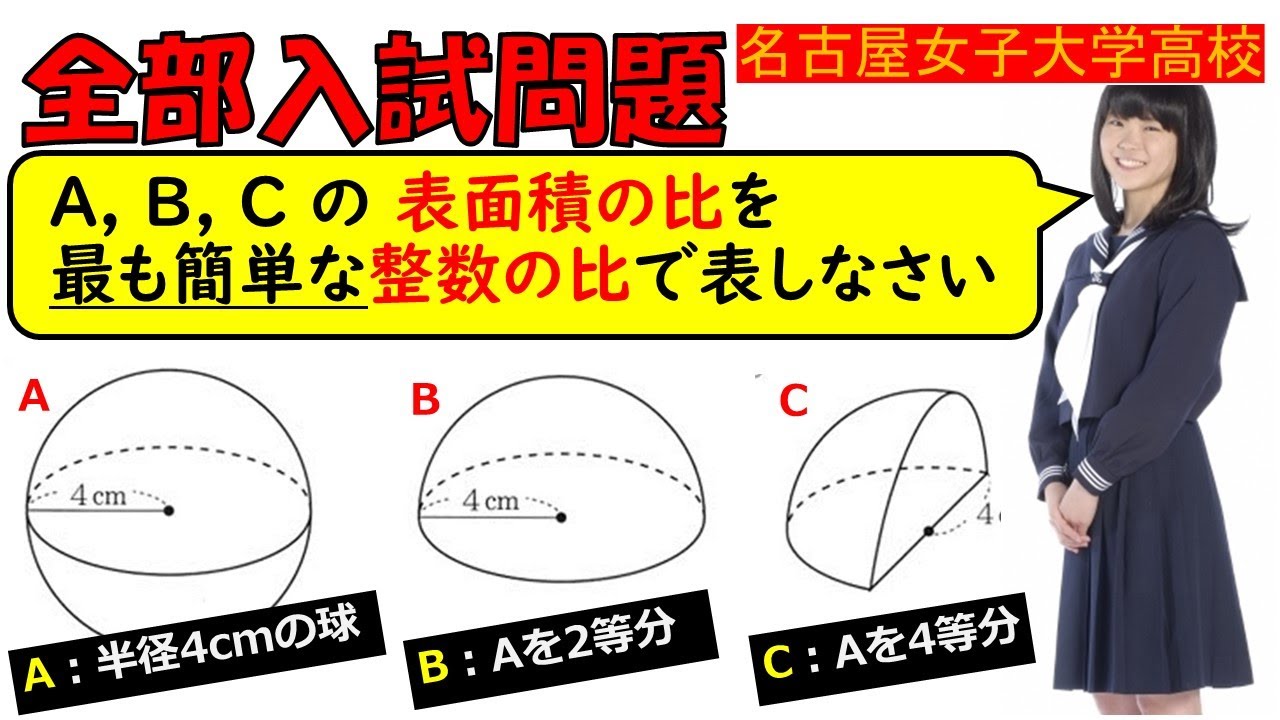
A:半径4㎝の球、B:Aの二等分、C:Aの四等分の表面積の比を最も簡単な整数の比で表しなさい。
この動画を見る
A:半径4㎝の球、B:Aの二等分、C:Aの四等分の表面積の比を最も簡単な整数の比で表しなさい。
【とても大切…!】図形:国立高等専門学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#空間図形#立体図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
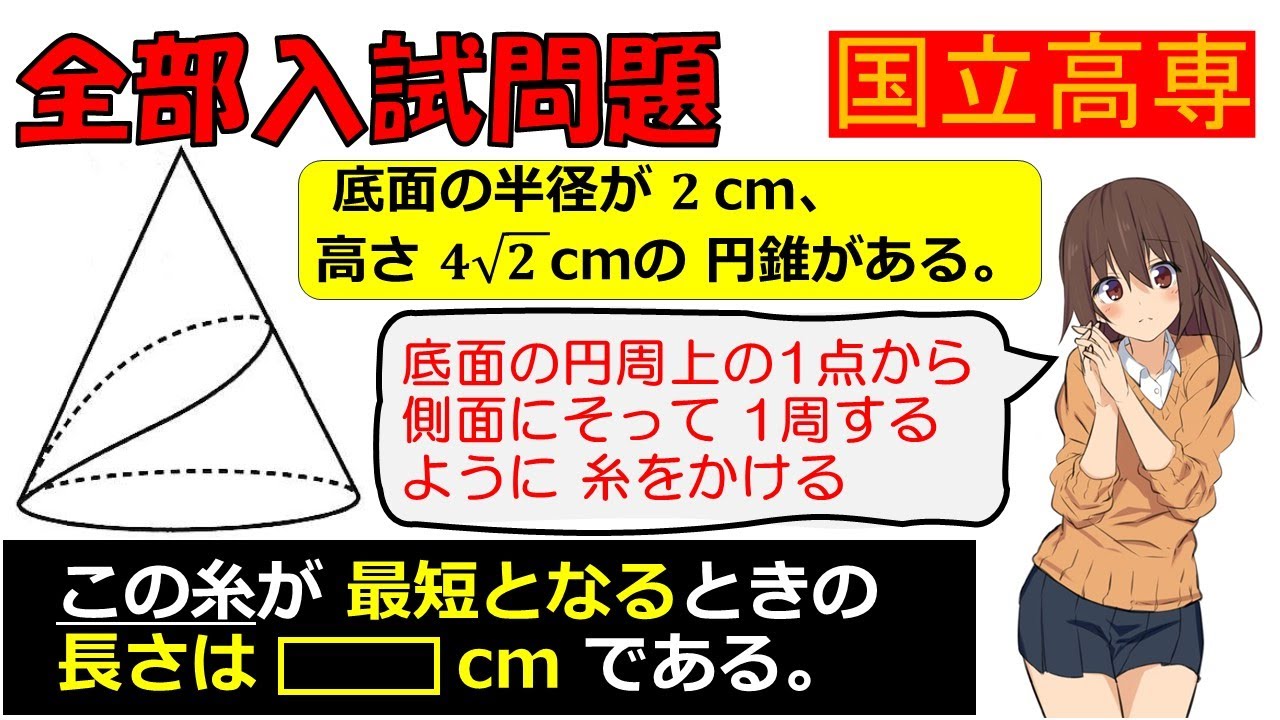
$底面の半径が2cm、高さ4\sqrt{2}cmの円錐がある。$
$底面の円周上の一点から側面に沿って一周するように糸を書ける$
$この糸が最短となるときの長さは\boxed{ }cmである。$
この動画を見る
$底面の半径が2cm、高さ4\sqrt{2}cmの円錐がある。$
$底面の円周上の一点から側面に沿って一周するように糸を書ける$
$この糸が最短となるときの長さは\boxed{ }cmである。$
立方体の中にある四面体の体積
単元:
#数学(中学生)#中1数学#空間図形#高校入試過去問(数学)#早稲田大学系属早稲田佐賀高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
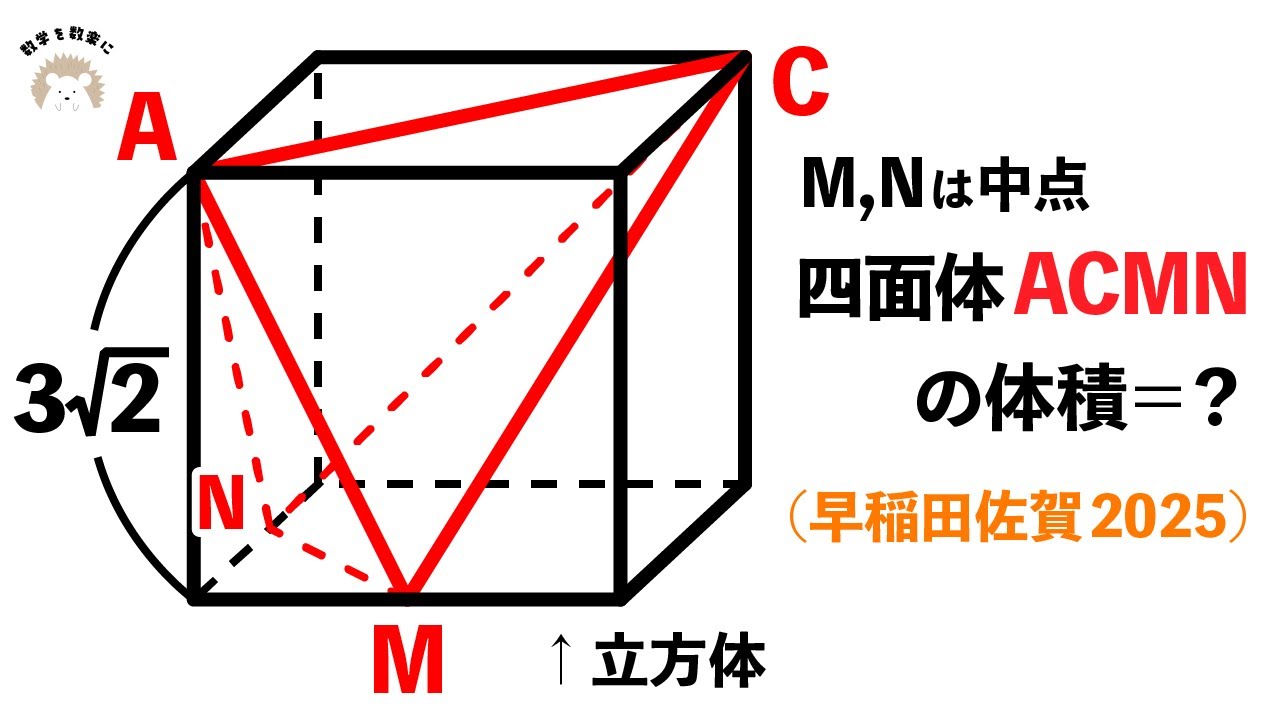
M、Nは中点。四面体ACMNの体積=?
*図は動画内参照
この動画を見る
M、Nは中点。四面体ACMNの体積=?
*図は動画内参照
このヒモの長さ分かるかな?

単元:
#数学(中学生)#中1数学#空間図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
図は、底面の半径が3、母線の長さが12の円錐である。
※図は動画内参照
円錐にかかっているヒモの長さは?
この動画を見る
図は、底面の半径が3、母線の長さが12の円錐である。
※図は動画内参照
円錐にかかっているヒモの長さは?
立方体の対角線の長さ
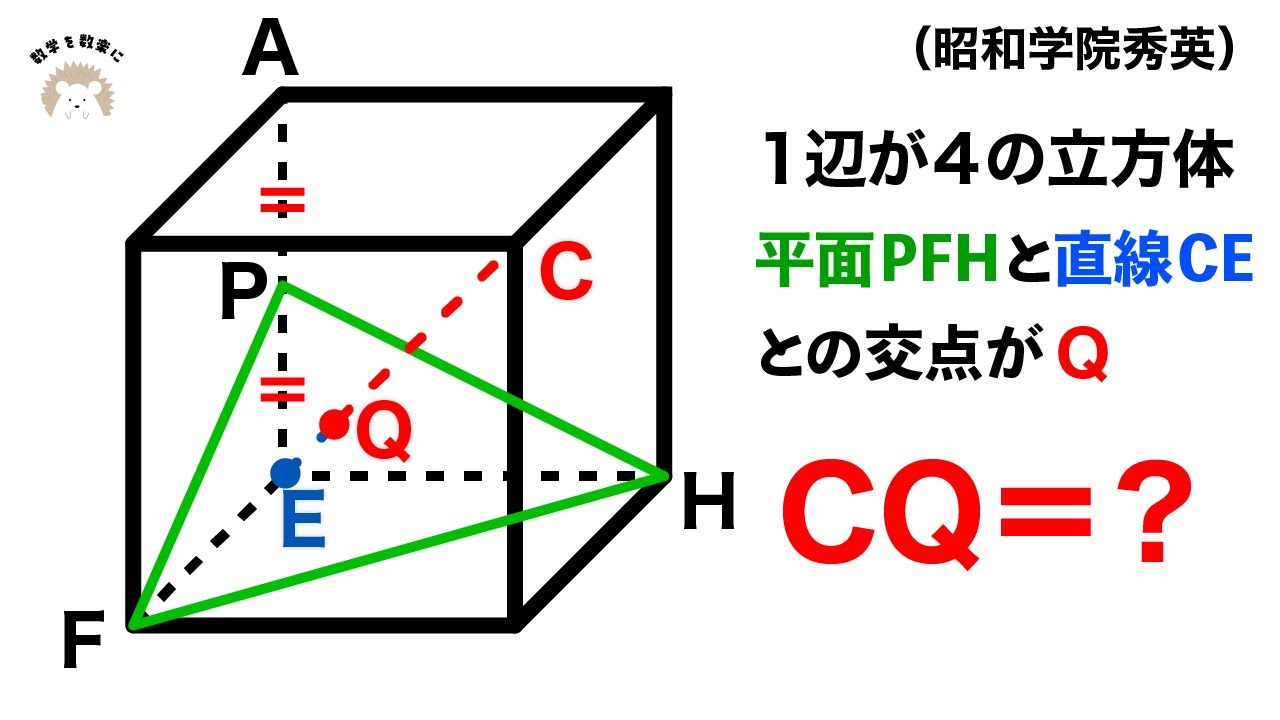
空間上の線分の長さ 昭和学院秀英
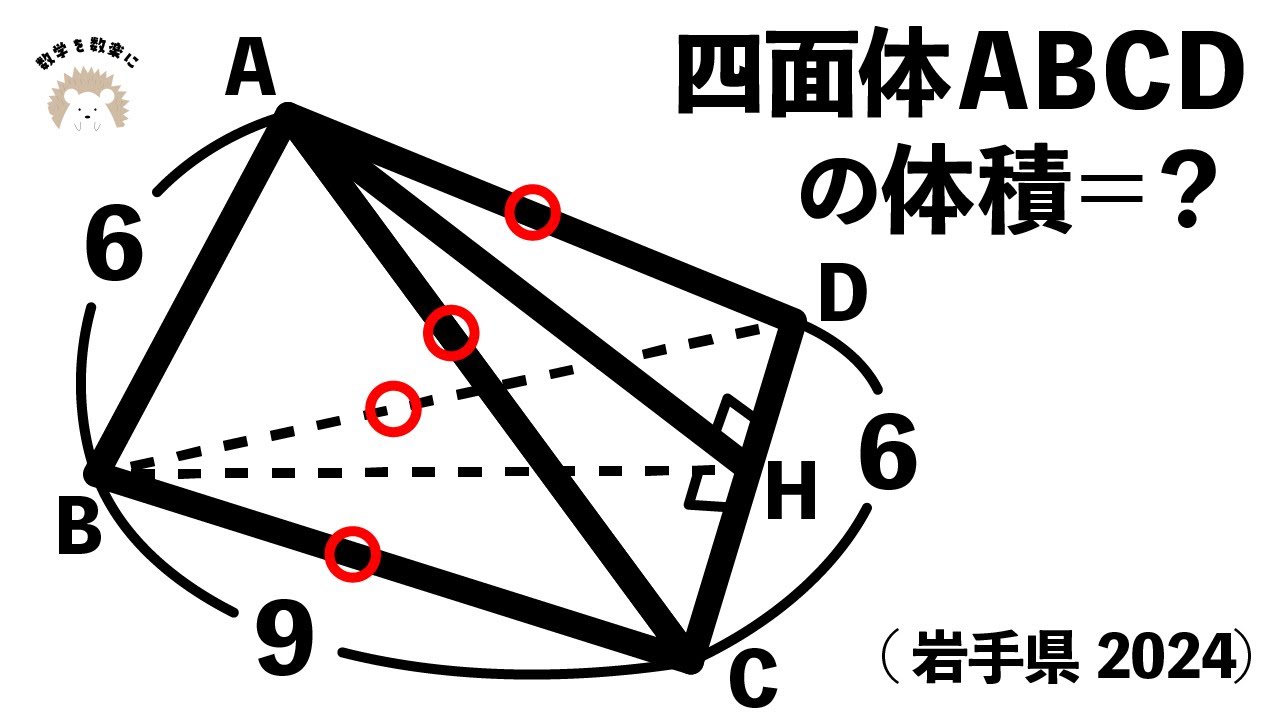
2024年岩手県のラスボス 四面体の体積
【中学数学】立体の体積と表面積の求め方~どこよりも丁寧に~ 6-4【中1数学】

単元:
#数学(中学生)#中1数学#空間図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
【中学数学】~どこよりも丁寧に~ 6-4【中1数学】
「立体の体積と表面積の求め方」について解説しています。
この動画を見る
【中学数学】~どこよりも丁寧に~ 6-4【中1数学】
「立体の体積と表面積の求め方」について解説しています。
【保存版】立体の展開図のイメージ

【中学数学】回転体と投影図~どこよりも丁寧に~【中1数学】

単元:
#算数(中学受験)#数学(中学生)#中1数学#空間図形#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
【中学数学】回転体と投影図解説動画です
この動画を見る
【中学数学】回転体と投影図解説動画です
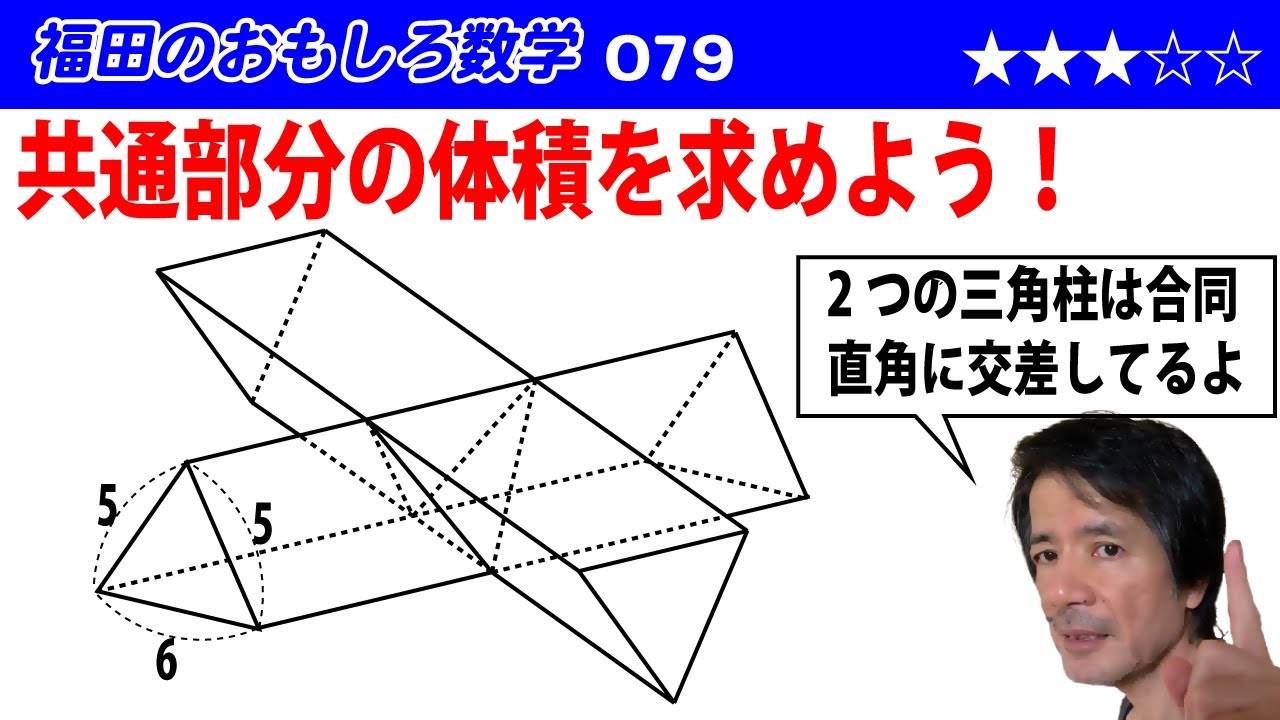
福田のおもしろ数学079〜交差する三角柱の共通部分の体積
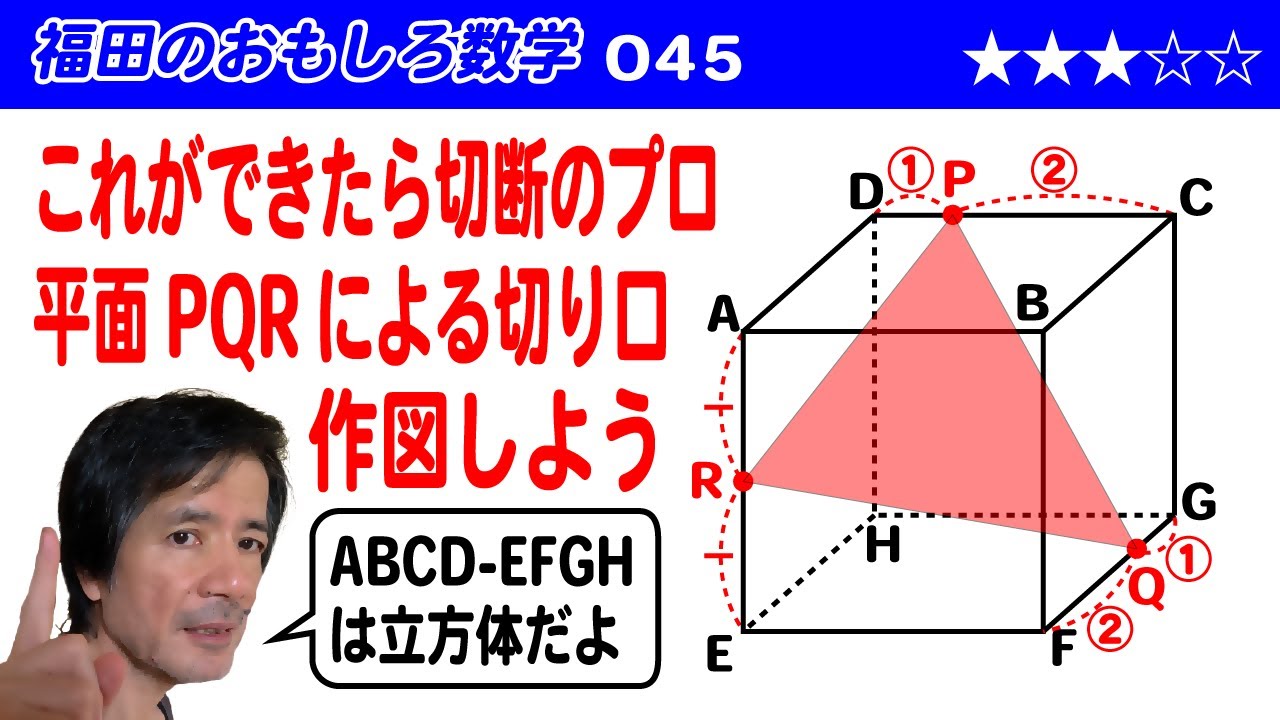
福田のおもしろ数学045〜これができたら切断のプロ〜立方体の切断
単元:
#算数(中学受験)#数学(中学生)#中1数学#空間図形#立体図形#立体切断
指導講師:
福田次郎
問題文全文(内容文):
立方体 ABCD ー EFGH を 3 点 P , Q , R を通る平面で切ったときの切り口を作図せよ。
※図は動画内参照
この動画を見る
立方体 ABCD ー EFGH を 3 点 P , Q , R を通る平面で切ったときの切り口を作図せよ。
※図は動画内参照
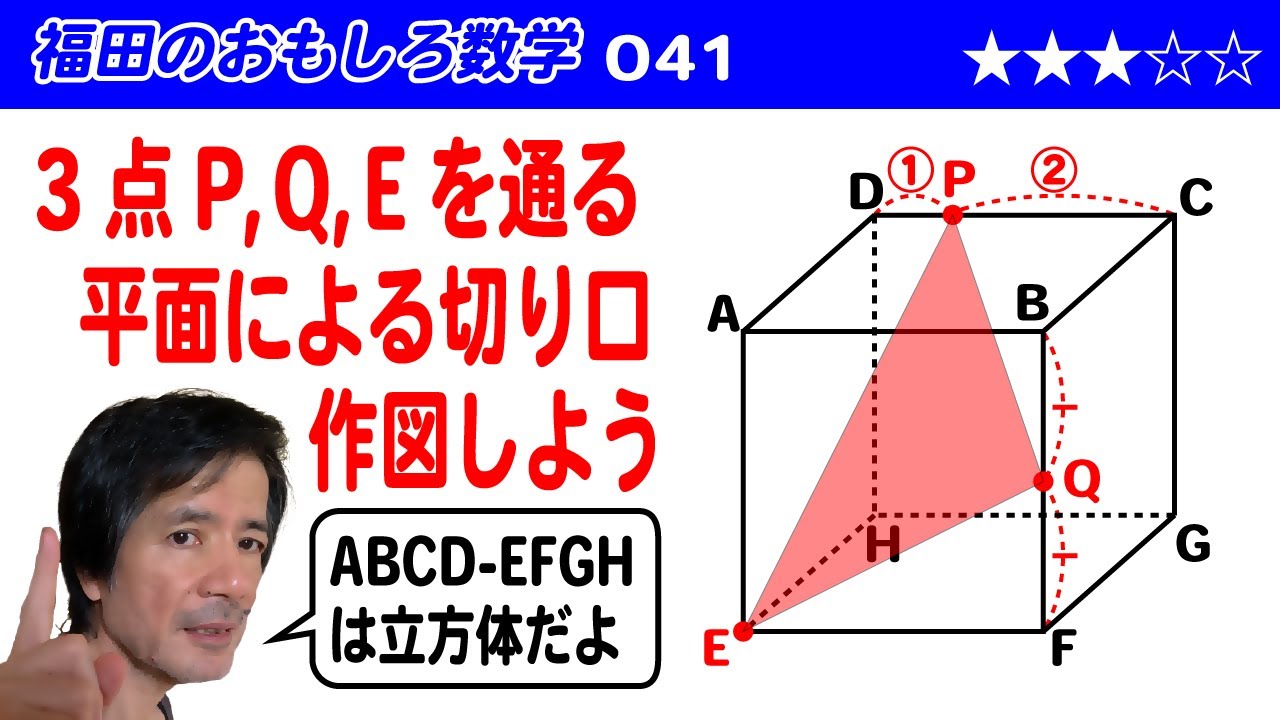
福田のおもしろ数学041〜立体の切断〜立方体を切った切り口
単元:
#算数(中学受験)#数学(中学生)#中1数学#空間図形#立体図形#立体切断
指導講師:
福田次郎
問題文全文(内容文):
立方体 ABCD-EFGH を 3 点 P,Q,E を通る平面で切ったときの切り口を作図せよ。
※図は動画内参照
この動画を見る
立方体 ABCD-EFGH を 3 点 P,Q,E を通る平面で切ったときの切り口を作図せよ。
※図は動画内参照
【中学数学】円柱の表面積の問題~2023年度大阪府B問題~【高校受験】

単元:
#数学(中学生)#中1数学#空間図形#高校入試過去問(数学)#大阪府高等学校
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
底面が半径4cm、高さがaの円柱の表面積が120πのとき、aの値を求めよ
5秒で解けます
この動画を見る
底面が半径4cm、高さがaの円柱の表面積が120πのとき、aの値を求めよ
5秒で解けます
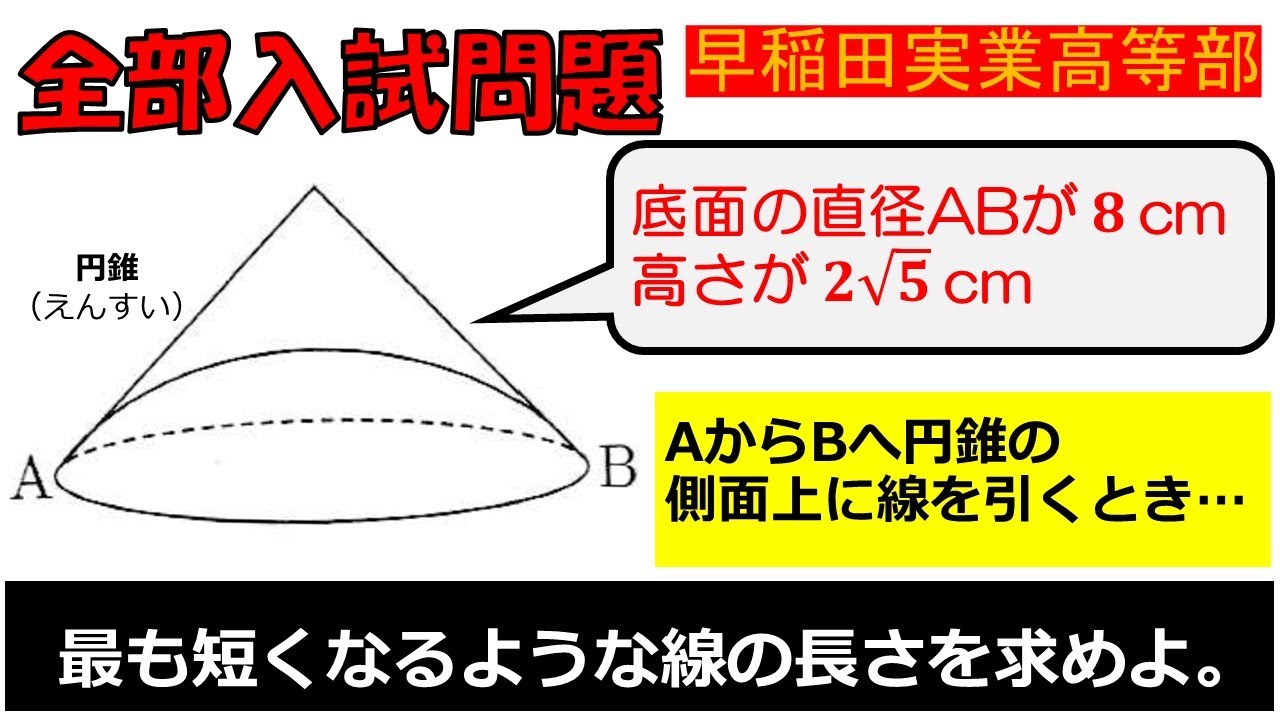
【カギは最初にある!】立体図形:早稲田大学系属早稲田実業学校高等部~全国入試問題解法
単元:
#数学(中学生)#中1数学#空間図形#高校入試過去問(数学)#早稲田大学系属早稲田実業学校高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
底面の直径$ AB $が8cm、高さが$ 2\sqrt5$cmである.
AからBへ円錐の側面上に線を引くとき,
最も短くなるような線の長さを求めよ.
早稲田実業高等部過去問
この動画を見る
底面の直径$ AB $が8cm、高さが$ 2\sqrt5$cmである.
AからBへ円錐の側面上に線を引くとき,
最も短くなるような線の長さを求めよ.
早稲田実業高等部過去問
【中学数学】色々な立体と多面体~分かりやすく丁寧に~【中1数学】

図形問題は補助線が命~全国入試問題解法 #shorts #数学 #mathematics #高校入試 #裏ワザ
単元:
#数学(中学生)#中1数学#空間図形#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
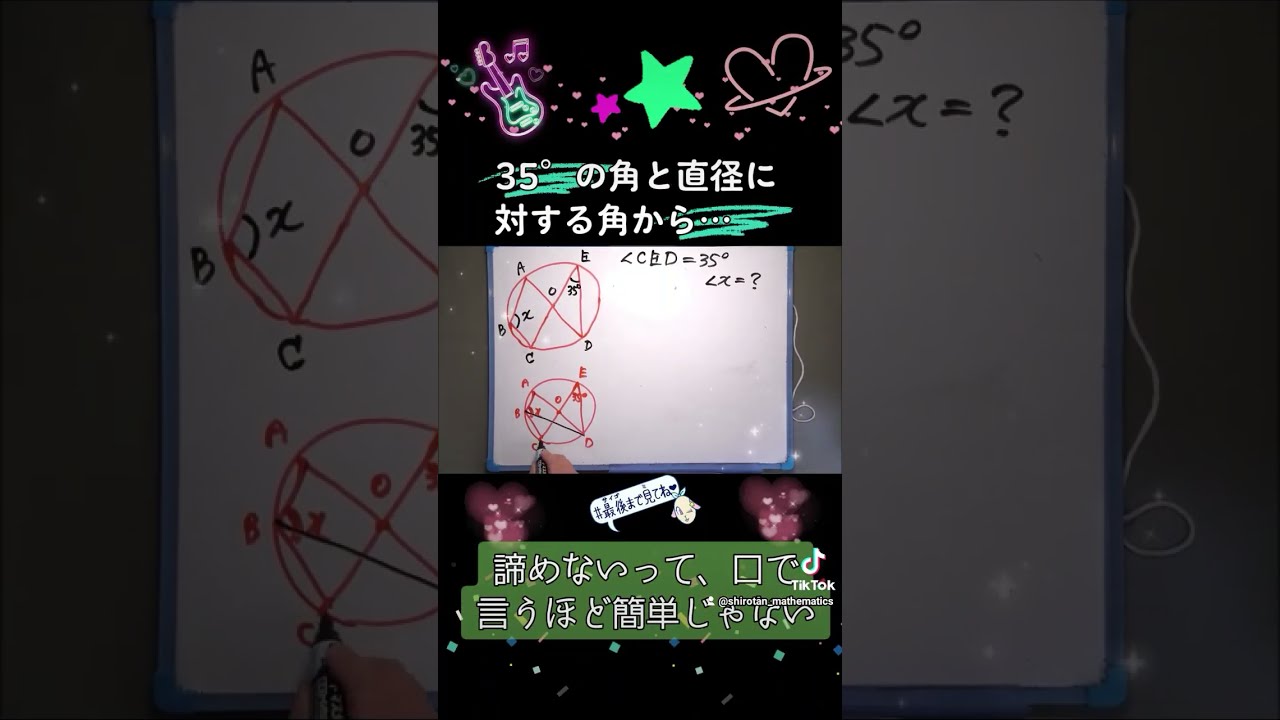
線分AD,CEはともに円Oの中心を通る.
$ \angle x$の大きさを求めなさい.
和歌山県高校過去問
この動画を見る
線分AD,CEはともに円Oの中心を通る.
$ \angle x$の大きさを求めなさい.
和歌山県高校過去問
図で理解する球の体積の公式~古森もぐちなぷぷに数学教えてみた~

2023高校入試数学解説95問目 回転体の体積 茨城県
単元:
#数学(中学生)#中1数学#空間図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
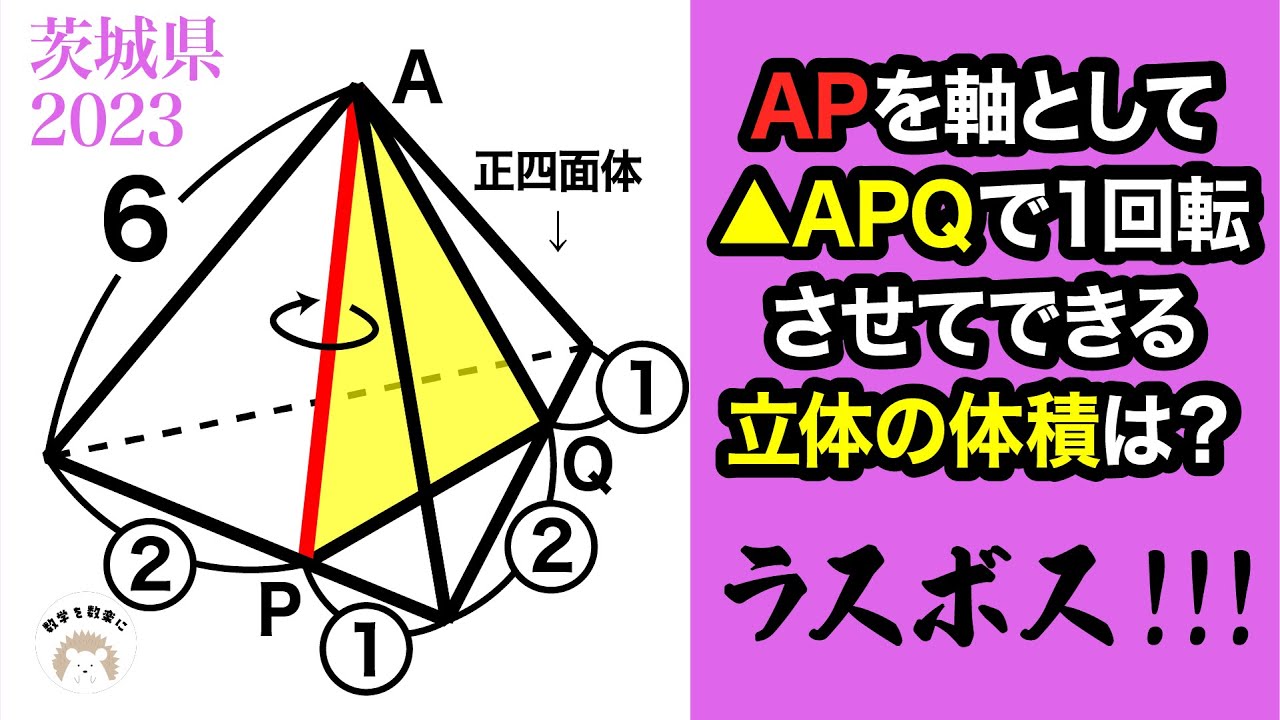
APを軸として△APQで1回転させてできる立体の体積は?
*図は動画内参照
2023茨城県
この動画を見る
APを軸として△APQで1回転させてできる立体の体積は?
*図は動画内参照
2023茨城県
【中学数学】数学用語チェック絵本 中1の用語”せめて”これだけは覚えよう!!

単元:
#数学(中学生)#中1数学#正の数・負の数#方程式#比例・反比例#空間図形#資料の活用#文字と式#平面図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
中1で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ!vol.1~7の方も見てね♪
この動画を見る
中1で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ!vol.1~7の方も見てね♪
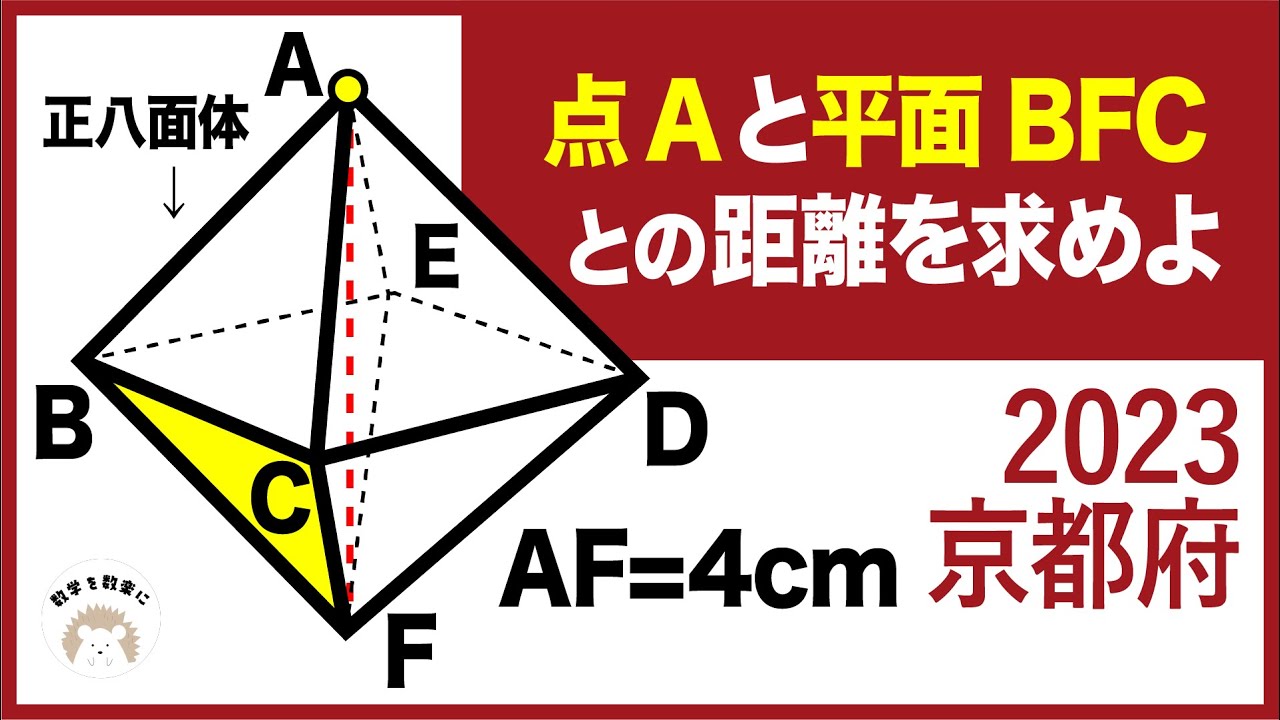
2023高校入試数学解説89問目 正八面体 京都府
単元:
#数学(中学生)#中1数学#空間図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
AF=4㎝
正八面体の1辺の長さは?
*図は動画内参照
2023京都府
この動画を見る
AF=4㎝
正八面体の1辺の長さは?
*図は動画内参照
2023京都府
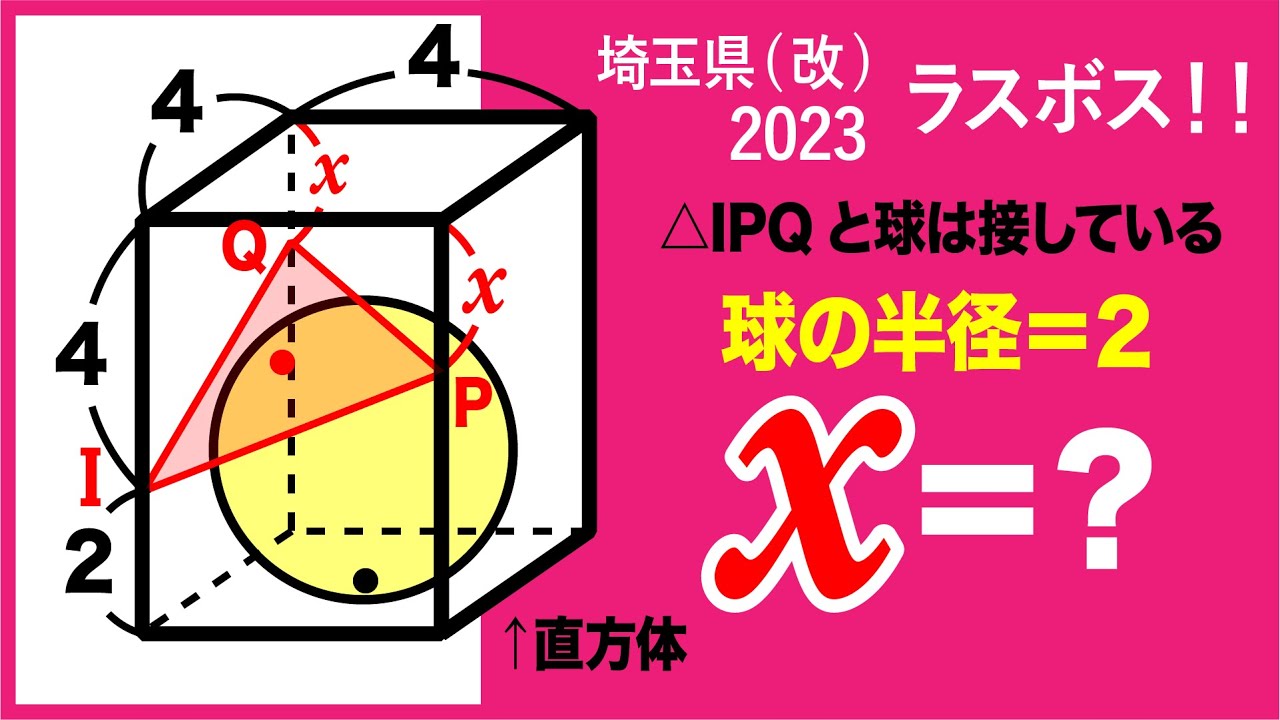
2023高校入試数学解説88問目 直方体と内接球 埼玉県学校選択問題(改)
単元:
#数学(中学生)#中1数学#空間図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
△IPQと球は接している
球の半径=2
x=?
*図は動画内参照
2023埼玉県(改)ラスボス
この動画を見る
△IPQと球は接している
球の半径=2
x=?
*図は動画内参照
2023埼玉県(改)ラスボス
高等学校入学試験予想問題:秋田県公立高等学校~全部入試問題
単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#2次方程式#空間図形#相似な図形#文章題#文章題その他#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$\dfrac{15}{2}\times \left(-\dfrac{4}{5}\right)$
(2)$ 10a-(6a+8)$
(3)$ 27ab^2\div 9ab $
(4)二次方程式$ x^2-3x+1=0$を解け.
$ \boxed{2}$
(1)底面が1辺6cmの正方形,体積$ 96cm^3$の四角錐の高さは?
(2)$ 4 \lt \sqrt a \lt \dfrac{13}{3}$に当てはまるaの値をすべて求めよ.
(3)$ \ell \parallel m $のとき,$ \angle x $は?
$ \boxed{3}$
n番目の白タイルの枚数をnの式で表せ.
この動画を見る
$ \boxed{1}$
(1)$\dfrac{15}{2}\times \left(-\dfrac{4}{5}\right)$
(2)$ 10a-(6a+8)$
(3)$ 27ab^2\div 9ab $
(4)二次方程式$ x^2-3x+1=0$を解け.
$ \boxed{2}$
(1)底面が1辺6cmの正方形,体積$ 96cm^3$の四角錐の高さは?
(2)$ 4 \lt \sqrt a \lt \dfrac{13}{3}$に当てはまるaの値をすべて求めよ.
(3)$ \ell \parallel m $のとき,$ \angle x $は?
$ \boxed{3}$
n番目の白タイルの枚数をnの式で表せ.
2023高校入試数学解説76問目 空間上の平面 愛知県

単元:
#数学(中学生)#中1数学#空間図形#平面図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
空間内の平面について正しく述べたものを全て選べ
ア.異なる2点を含む平面は1つしかない
イ.交わる2直線を含む平面は1つしかない
ウ.平行な2直線を含む平面は1つしかない
エ.同じ直線上にある3点を含む平面は1つしかない
2023愛知県
この動画を見る
空間内の平面について正しく述べたものを全て選べ
ア.異なる2点を含む平面は1つしかない
イ.交わる2直線を含む平面は1つしかない
ウ.平行な2直線を含む平面は1つしかない
エ.同じ直線上にある3点を含む平面は1つしかない
2023愛知県
【裏技】知ってないのヤバいレベル

球の表面積を一瞬で理解

単元:
#数学(中学生)#中1数学#空間図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記質問の解説動画です
球の表面積が$4 \pi r^2$が納得できないです
この動画を見る
下記質問の解説動画です
球の表面積が$4 \pi r^2$が納得できないです
球の表面積を直感で理解させます

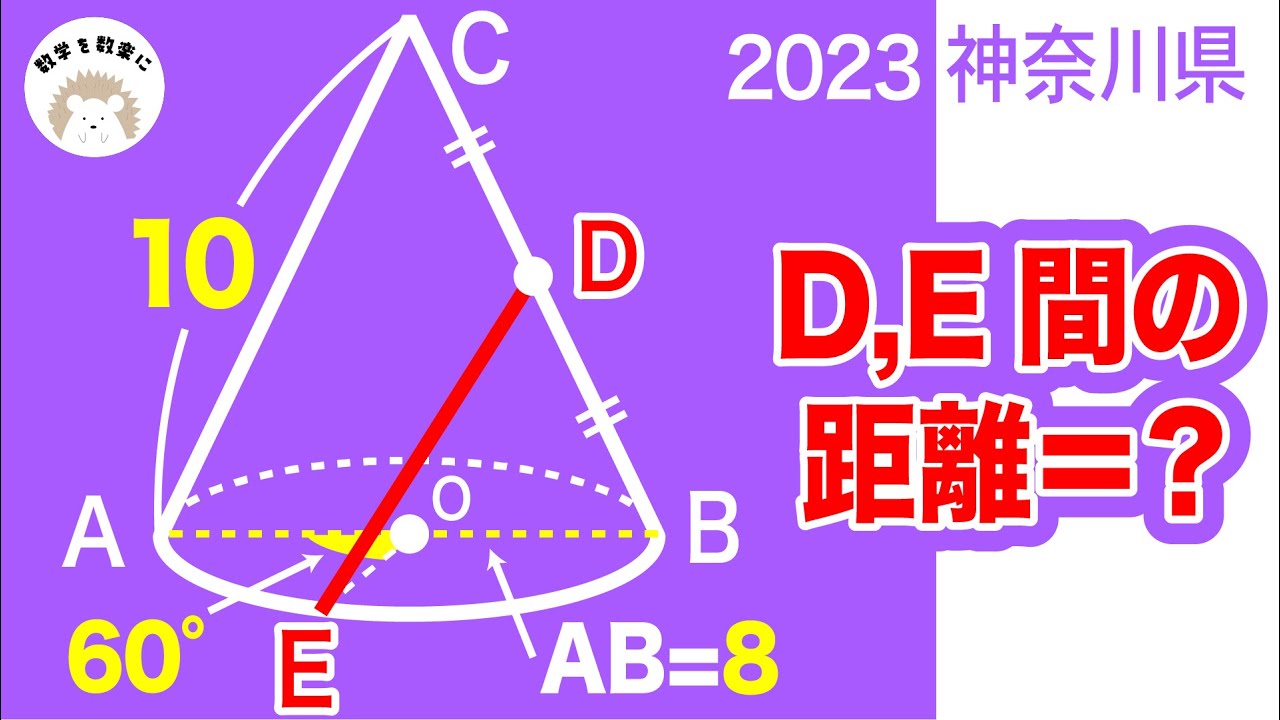
2023高校入試数学解説52問目 空間上の2点間の距離 円錐 神奈川県
コミカルな気分で空間図形をマスターする動画~全国入試問題解法 #shorts #数学 #高校受験 #sound
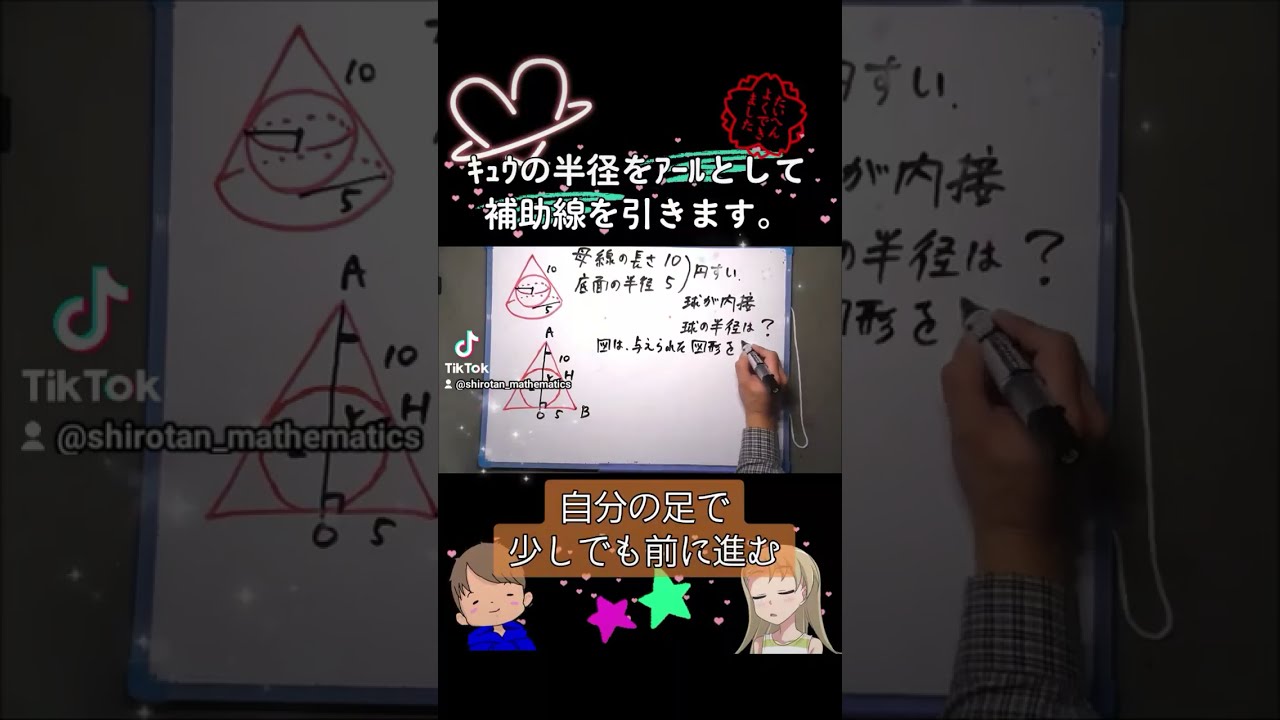
単元:
#数学(中学生)#中1数学#空間図形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
母線の長さが10,底面の円の半径が5の円錐に球が内接している.
球の半径は$ \Box $である.
大阪星光高校過去問
この動画を見る
母線の長さが10,底面の円の半径が5の円錐に球が内接している.
球の半径は$ \Box $である.
大阪星光高校過去問
【裏技】なんで先教えてくれんかったん?

