中１数学
中１数学
正負の足し算引き算できる？
中1の4月に出来て欲しい計算
単元：
#数学(中学生)#中１数学#正の数・負の数
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
①$(+2)+(+5)$
②$(+4)+(-2)$
③$(-7)+(+20)$
④$(+2)-(+1)$
⑤$(+9)-(+10)$
⑥$(-5)-(+5)$
⑦$(+1)-(-3)$
この動画を見る
①$(+2)+(+5)$
②$(+4)+(-2)$
③$(-7)+(+20)$
④$(+2)-(+1)$
⑤$(+9)-(+10)$
⑥$(-5)-(+5)$
⑦$(+1)-(-3)$
偶数
文字式を解くにはパターンがある～全国入試問題解法 #shorts, #数学, #高校入試, #頭の体操
単元：
#数学(中学生)#中１数学#文字と式
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ x+y=-1,xy=-\dfrac{3}{5}$のとき,
$ x^2-3xy+y^2$の値を求めなさい.
法政大第二高校過去問
この動画を見る
$ x+y=-1,xy=-\dfrac{3}{5}$のとき,
$ x^2-3xy+y^2$の値を求めなさい.
法政大第二高校過去問
それぞれの角は出ていないけど和は求まります！
単元：
#数学(中学生)#中１数学#中２数学#平面図形#三角形と四角形
指導講師：
数学を数楽に
問題文全文(内容文)：
$\angle x+\angle y+\angle z=$
＊図は動画内参照
この動画を見る
$\angle x+\angle y+\angle z=$
＊図は動画内参照
正負の数の計算です。
中1の計算
これなんで？
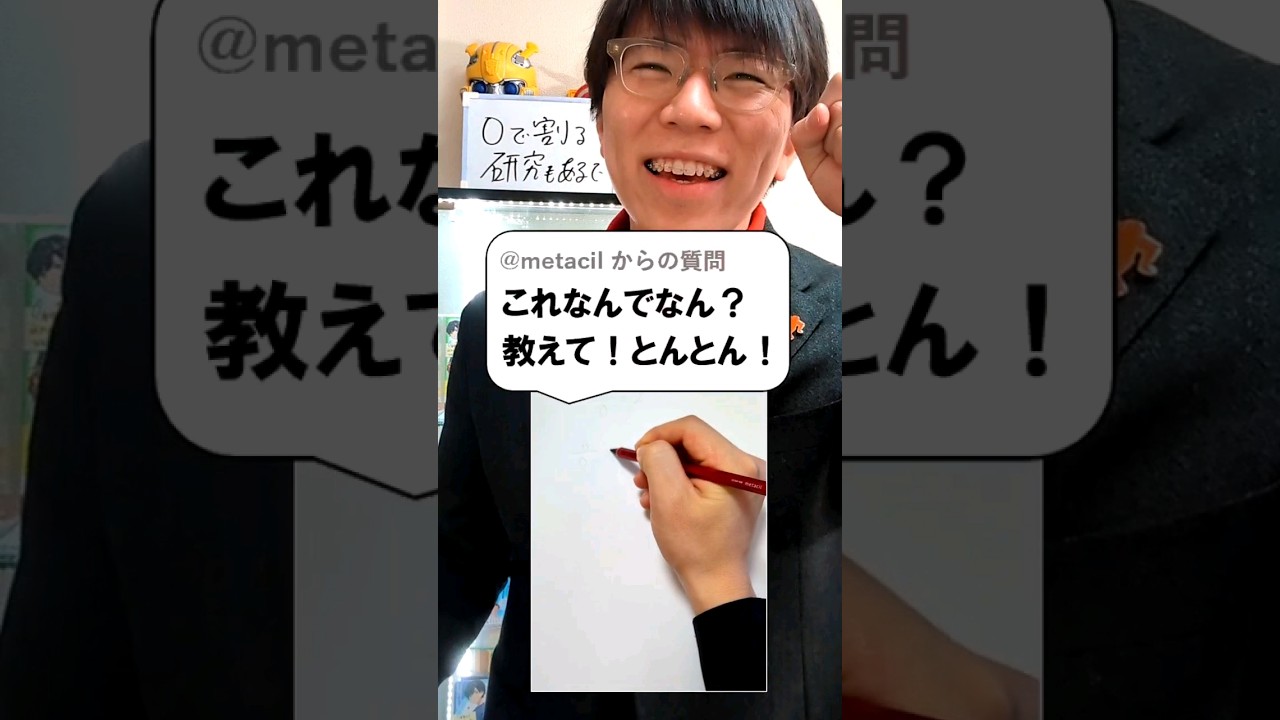
福田のおもしろ数学086〜1分チャレンジ〜正三角形2個で作る核を求めよう
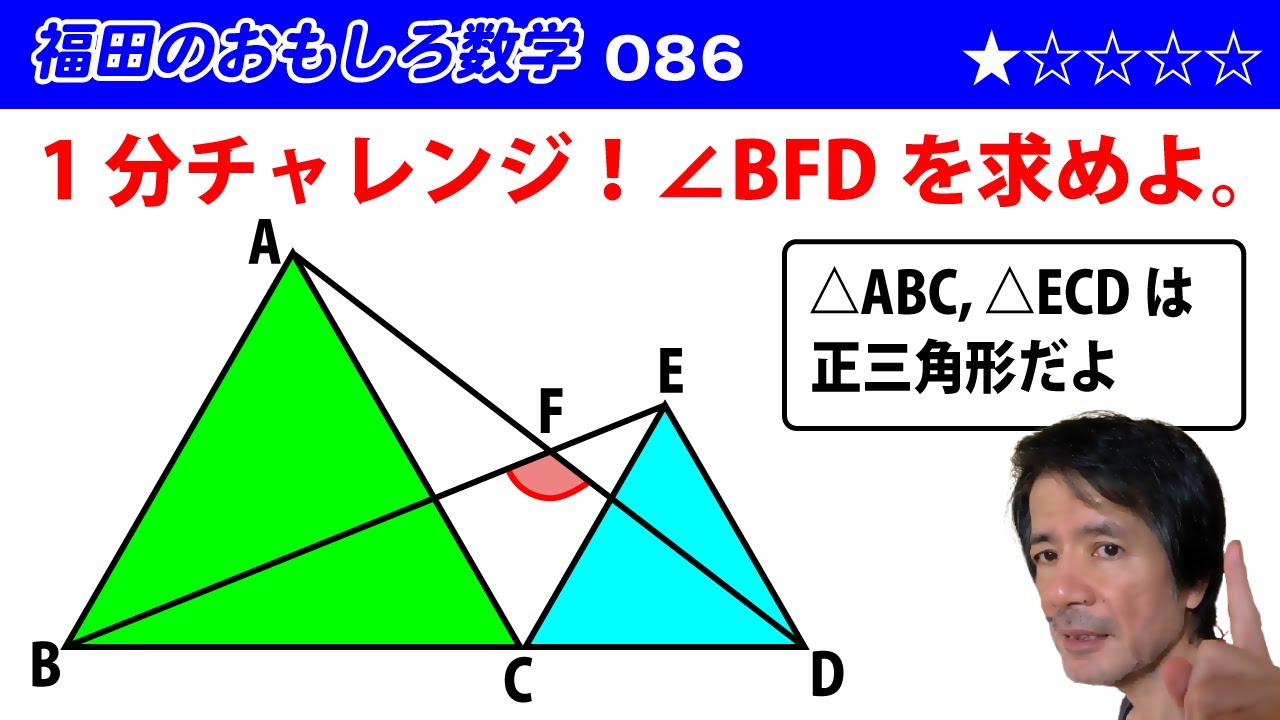
福田のおもしろ数学079〜交差する三角柱の共通部分の体積
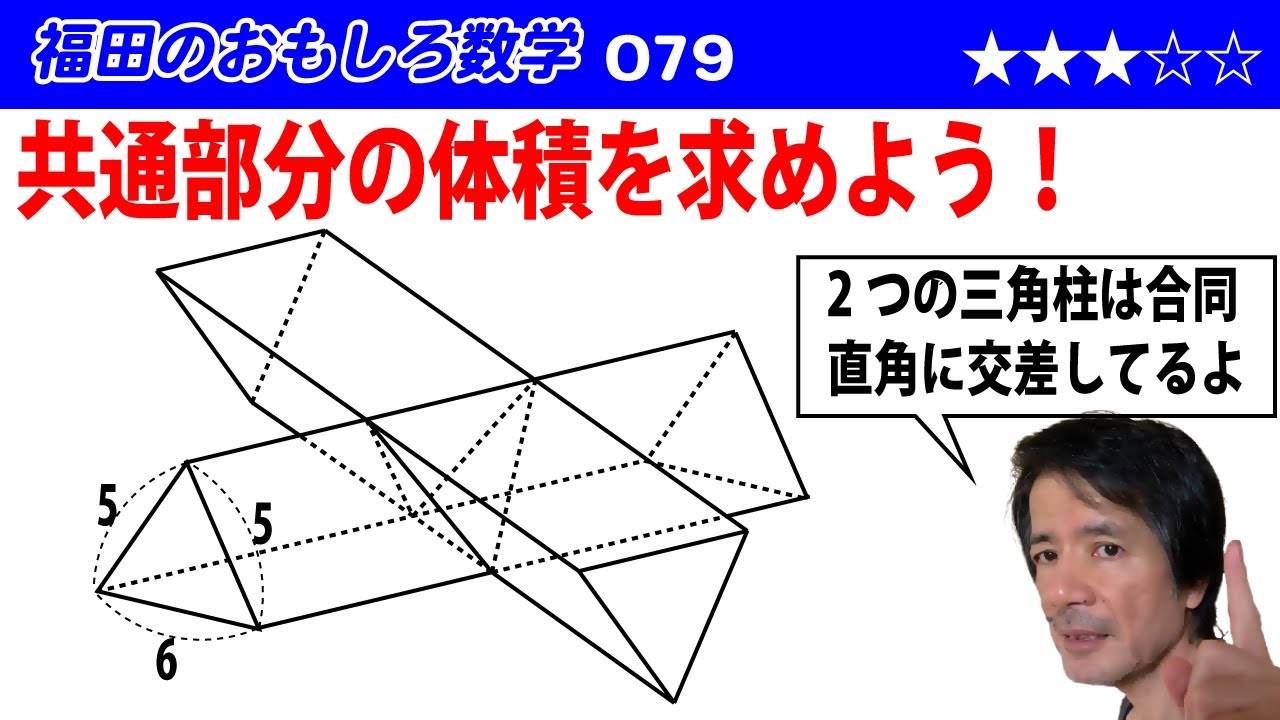
福田のおもしろ数学075〜1分チャレンジ〜扇形から作る円錐の体積
千葉県の難問！？平面図形2024
2024神奈川県の平面図形の難問
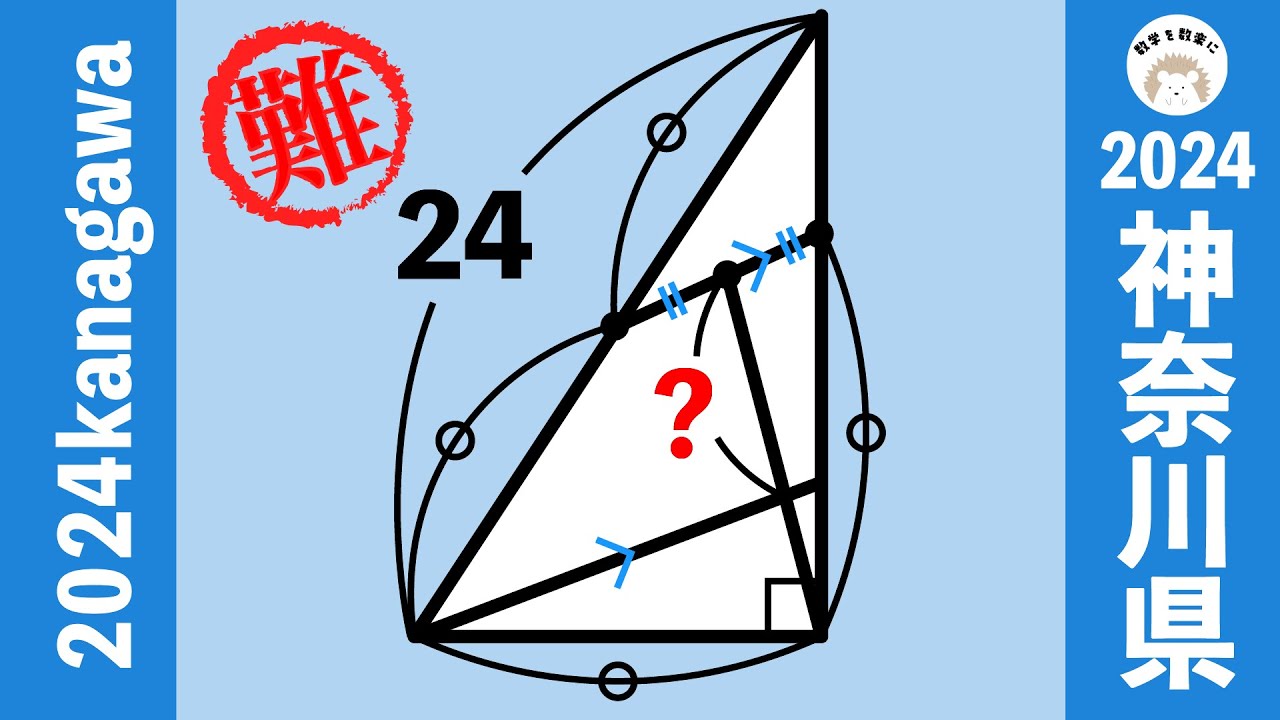
平面図形 2024京都府（改）
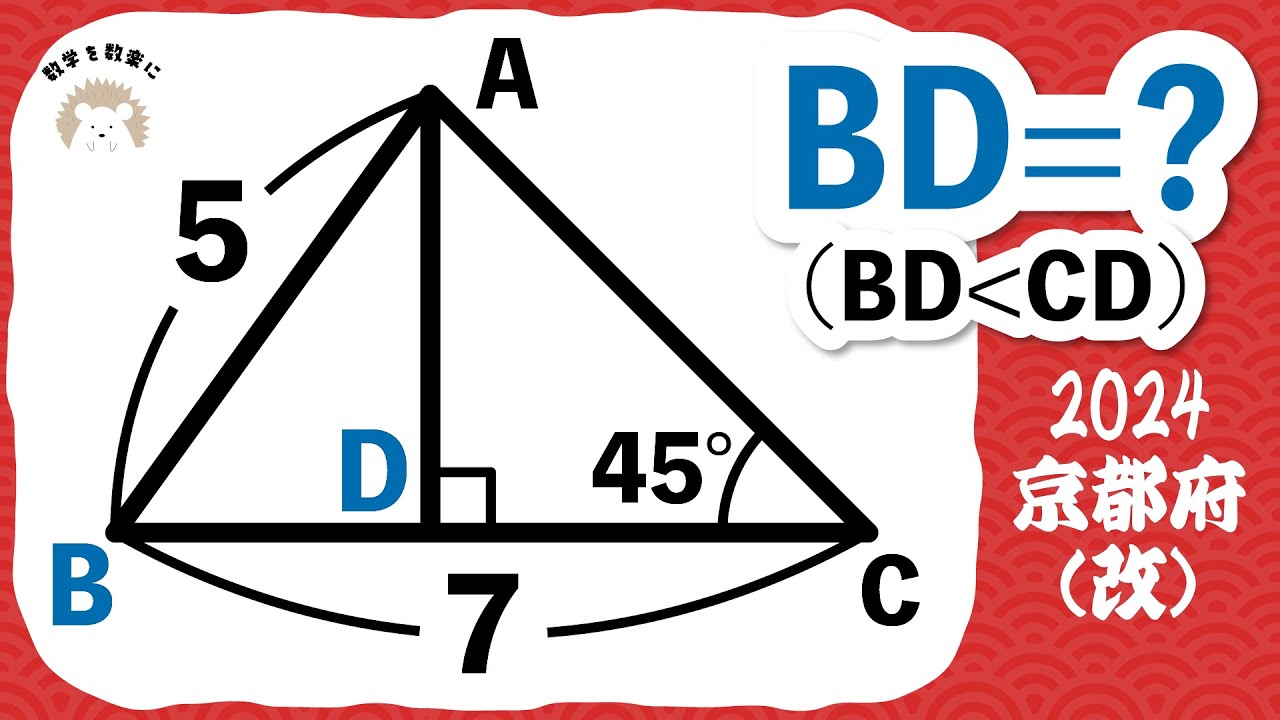
福田のおもしろ数学045〜これができたら切断のプロ〜立方体の切断
単元：
#算数(中学受験)#数学(中学生)#中１数学#空間図形#立体図形#立体切断
指導講師：
福田次郎
問題文全文(内容文)：
立方体 ABCD ー EFGH を 3 点 P , Q , R を通る平面で切ったときの切り口を作図せよ。
※図は動画内参照
この動画を見る
立方体 ABCD ー EFGH を 3 点 P , Q , R を通る平面で切ったときの切り口を作図せよ。
※図は動画内参照
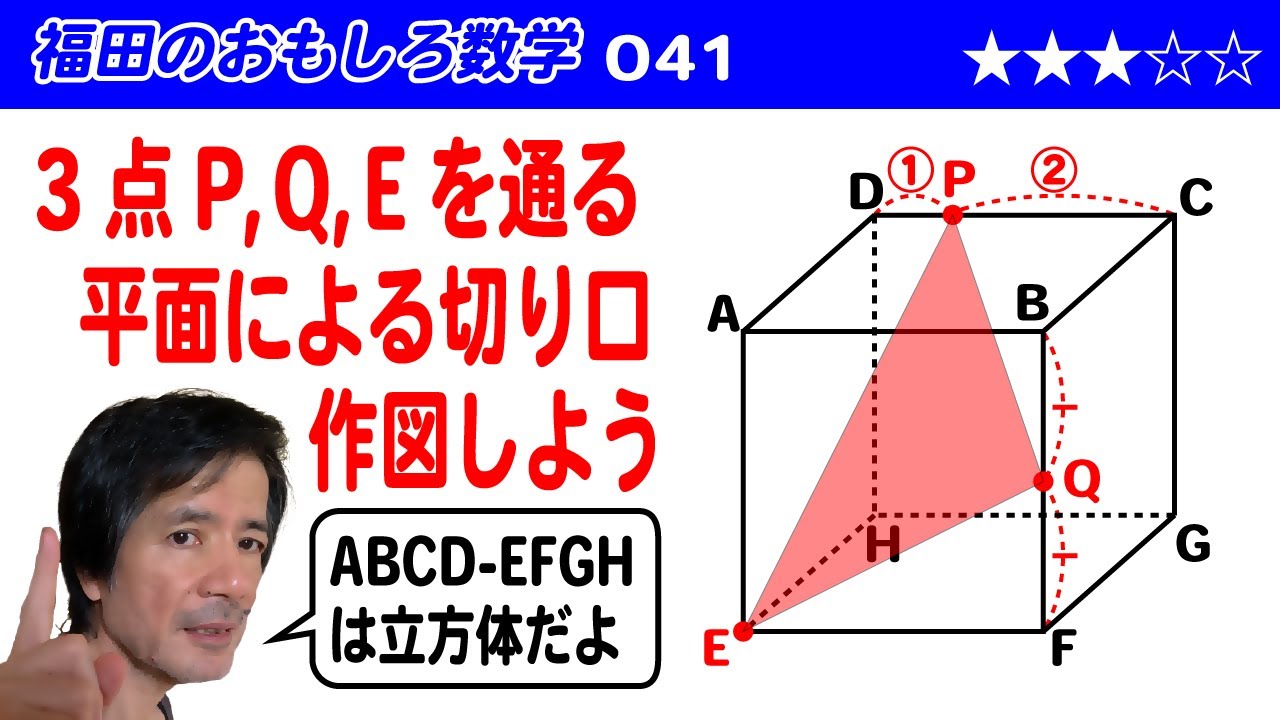
福田のおもしろ数学041〜立体の切断〜立方体を切った切り口
単元：
#算数(中学受験)#数学(中学生)#中１数学#空間図形#立体図形#立体切断
指導講師：
福田次郎
問題文全文(内容文)：
立方体 ABCD-EFGH を 3 点 P,Q,E を通る平面で切ったときの切り口を作図せよ。
※図は動画内参照
この動画を見る
立方体 ABCD-EFGH を 3 点 P,Q,E を通る平面で切ったときの切り口を作図せよ。
※図は動画内参照
これなんで？
【フル】なぜ年齢が当てられるのか？
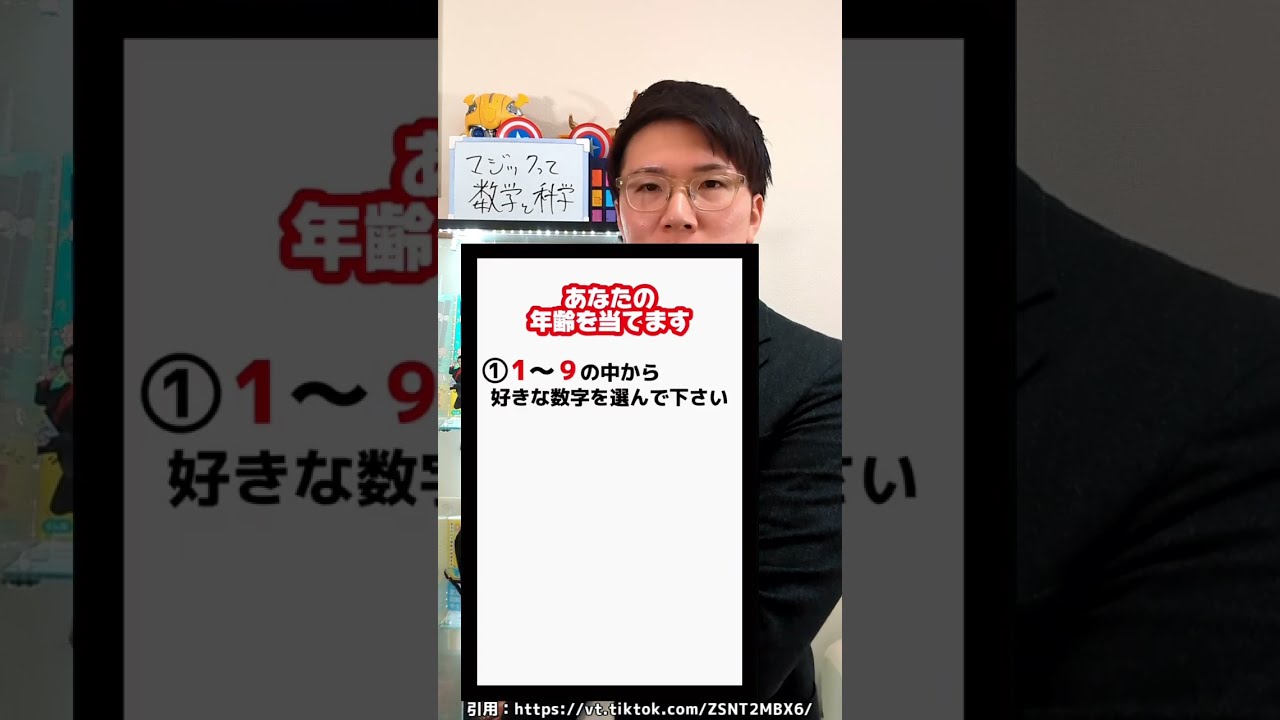
福田のおもしろ数学016〜ジュニア数学オリンピック予選問題〜正三角形の面積
単元：
#算数(中学受験)#数学(中学生)#中１数学#中２数学#数学検定・数学甲子園・数学オリンピック等#平面図形#角度と面積#平面図形#三角形と四角形#数学オリンピック
指導講師：
福田次郎
問題文全文(内容文)：
正三角形 ABC を図のように、 3 辺に平行な線分を 1 本ずっ引いて分割した。書かれている数は分割してできた正三角形の面積を表している。このとき、正三角形の面積を求めよ。
※図は動画内参照
ジュニア数学オリンピック過去問
この動画を見る
正三角形 ABC を図のように、 3 辺に平行な線分を 1 本ずっ引いて分割した。書かれている数は分割してできた正三角形の面積を表している。このとき、正三角形の面積を求めよ。
※図は動画内参照
ジュニア数学オリンピック過去問
【中学数学】箱ひげ図データの分析～2022年度北海道公立高校入試～【高校受験】
単元：
#数学(中学生)#中１数学#資料の活用#高校入試過去問(数学)#北海道公立高校入試
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
北海道公立高校2022年数学過去問
春奈さんたちの中学校では, 3年生のA組30人全員と, B組30人全員の50m走の記録を調査 しました。 次の問いに答えなさい。
問1 図1は, A組, B組全員の記録を、 それぞれ箱ひげ図にまとめたものです。（図は動画内参照）
次の(1),(2) に答えなさい。
(1) B組の記録の第3四分位数を求めなさい
(2) データの散らばり (分布) の程度について、 図1から読みとれることとして
最も適当なものを、次のア~エから1つ選びなさい
ア範囲は, A組の方がB組よりも小さい。
イ四分位範囲は, A組の方がB組よりも大きい。
ウ平均値は, A組の方がB組よりも小さい。
エ最大値は, A組の方がB組よりも大きい。
この動画を見る
北海道公立高校2022年数学過去問
春奈さんたちの中学校では, 3年生のA組30人全員と, B組30人全員の50m走の記録を調査 しました。 次の問いに答えなさい。
問1 図1は, A組, B組全員の記録を、 それぞれ箱ひげ図にまとめたものです。（図は動画内参照）
次の(1),(2) に答えなさい。
(1) B組の記録の第3四分位数を求めなさい
(2) データの散らばり (分布) の程度について、 図1から読みとれることとして
最も適当なものを、次のア~エから1つ選びなさい
ア範囲は, A組の方がB組よりも小さい。
イ四分位範囲は, A組の方がB組よりも大きい。
ウ平均値は, A組の方がB組よりも小さい。
エ最大値は, A組の方がB組よりも大きい。
【式は2つ、文字は3つ…！】整数：慶応義塾女子高等学校～全国入試問題解法
単元：
#中１数学#中２数学#連立方程式#文字と式
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ \color{red}{整数x}$に$ \color{red}{6}$を加えると$ \color{red}{整数m}$の平方になり,
$ \color{red}{x}$から$ \color{red}{17}$を引くと$\color{red}{整数n}$の平方になる.
m,nはともに正として$ \color{orange}{m,n,x}$の値を求めなさい.
慶應女子高校過去問
この動画を見る
$ \color{red}{整数x}$に$ \color{red}{6}$を加えると$ \color{red}{整数m}$の平方になり,
$ \color{red}{x}$から$ \color{red}{17}$を引くと$\color{red}{整数n}$の平方になる.
m,nはともに正として$ \color{orange}{m,n,x}$の値を求めなさい.
慶應女子高校過去問
【中学数学】円柱の表面積の問題～2023年度大阪府B問題～【高校受験】
単元：
#数学(中学生)#中１数学#空間図形#高校入試過去問(数学)#大阪府高等学校
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
底面が半径4cm、高さがaの円柱の表面積が120πのとき、aの値を求めよ
5秒で解けます
この動画を見る
底面が半径4cm、高さがaの円柱の表面積が120πのとき、aの値を求めよ
5秒で解けます
【中学数学】2次関数の面積の問題演習～2023年大阪府B問題～【高校受験】
単元：
#数学(中学生)#中１数学#平面図形#高校入試過去問(数学)#大阪府高等学校
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
右図において, mは関数$y=ax^2$(aは正の定数)のグラフを表し,Iは関数$y=\frac{1}{3}x-1$のグラフを表す。Aは,Iとx軸との交点である。Bは,Aを通りy軸に平行な直線とmとの交点である。
Cは, Bを通りx軸に平行な直線とmとの交点のうちBと異なる点である。
Dは, Cを通りy軸に平行な直線との交点である。
Dは,Cを通りy軸に平行な直線との交点である。
四角形ABCDの面積は21cm²である, aの値を求めなさい。
この動画を見る
右図において, mは関数$y=ax^2$(aは正の定数)のグラフを表し,Iは関数$y=\frac{1}{3}x-1$のグラフを表す。Aは,Iとx軸との交点である。Bは,Aを通りy軸に平行な直線とmとの交点である。
Cは, Bを通りx軸に平行な直線とmとの交点のうちBと異なる点である。
Dは, Cを通りy軸に平行な直線との交点である。
Dは,Cを通りy軸に平行な直線との交点である。
四角形ABCDの面積は21cm²である, aの値を求めなさい。
【問題の本質は…！】文字式：大阪教育大学附属高等学校平野校舎～全国入試問題解法
単元：
#数学(中学生)#中１数学#文字と式
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ x^2-5x+3=0 $の2つの解を$ a,b $とする.
$ \dfrac{1}{a}+\dfrac{1}{b}$の値を求めよ.
大教大高校平野過去問
この動画を見る
$ x^2-5x+3=0 $の2つの解を$ a,b $とする.
$ \dfrac{1}{a}+\dfrac{1}{b}$の値を求めよ.
大教大高校平野過去問
【π（パイ）は円周率…！】整数：東京都立産業技術高等専門学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#文字と式
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ \pi \lt n \lt \sqrt{50}$を満たす整数$ n $を全て求めよ.
東京都立産業技術高等専門学校過去問
この動画を見る
$ \pi \lt n \lt \sqrt{50}$を満たす整数$ n $を全て求めよ.
東京都立産業技術高等専門学校過去問
【良問です…！】整数：秋田県～全国入試問題解法
単元：
#数学(中学生)#中１数学#文字と式
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ \dfrac{231}{n+2}$
整数となる$ n $の値を全て求めなさい.
※$ n $は100より小さい素数である.
秋田県入試問題過去問
この動画を見る
$ \dfrac{231}{n+2}$
整数となる$ n $の値を全て求めなさい.
※$ n $は100より小さい素数である.
秋田県入試問題過去問
【正面突破なら…！】文字式：慶応志木高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#文字と式#高校入試過去問(数学)#慶應義塾志木高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ x=\dfrac{7}{3+\sqrt2}$のとき,
$ (x-1)(x-2)(x-4)(x-5)$の値を求めよ.
慶応志木高校過去問
この動画を見る
$ x=\dfrac{7}{3+\sqrt2}$のとき,
$ (x-1)(x-2)(x-4)(x-5)$の値を求めよ.
慶応志木高校過去問
文字式は基本を抑えて手際よく！～全国入試問題解法 #shorts #数学 #高校入試 #頭の体操
単元：
#数学(中学生)#中１数学#文字と式
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ A=4x-1 $,$ B=-2x+3 $とするとき,次の計算しなさい.
$ -4A+3B+2A $
滋賀県入試問題過去問
この動画を見る
$ A=4x-1 $,$ B=-2x+3 $とするとき,次の計算しなさい.
$ -4A+3B+2A $
滋賀県入試問題過去問
15秒数で数学の解法！～全国入試問題解法 #shorts #数学 #高校入試 #動体視力
単元：
#数学(中学生)#中１数学#文字と式
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
3の倍数より1大きい数の2乗から,同じ3の倍数より1小さい数の2乗を
引いた差は,12の倍数である.
この考えがいつでも成り立つことを説明しなさい.
函館白百合学園高校過去問
この動画を見る
3の倍数より1大きい数の2乗から,同じ3の倍数より1小さい数の2乗を
引いた差は,12の倍数である.
この考えがいつでも成り立つことを説明しなさい.
函館白百合学園高校過去問
【良問です！】整数：徳島県公立高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#正の数・負の数#高校入試過去問(数学)#徳島県公立高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
1から9まで9つの自然数から異なる4つの数を選んでその積を
求めると,810になった.
この4つの数をすべて書きなさい.
徳島県公立高等学校過去問
この動画を見る
1から9まで9つの自然数から異なる4つの数を選んでその積を
求めると,810になった.
この4つの数をすべて書きなさい.
徳島県公立高等学校過去問