 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
【高校受験対策】数学-死守28

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#2次方程式#確率#2次関数#相似な図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$(- 4) + 3\times (- 3)$を計算しなさい。
②$\dfrac{2x - 1}{3} - \dfrac{3x + 1}{5}$を計算しなさい。
③$(\sqrt{12} + \sqrt{18})(\sqrt3 - \sqrt2)$を計算しなさい。
④$(x - 4)^ 2 + 2(x - 2) - 3$を因数分解しなさい。
⑤方程式$(x + 3)(x - 5) = 5x - 24$を解きなさい。
⑥次の連立方程式を解きなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x+5=3y-2 \\
3x+2y=16
\end{array}
\right.
\end{eqnarray}$
⑦関数$y=-3x^2$について、
$x$の値が1から3まで増加するときの変化の割合を求めなさい。
⑧1つのさいころを2回投げるとき、1回目に出た目の数が、
2回目に出た目の数の倍数となる確率を求めなさい。
⑨男子20人、好16人のクラスでテストを行ったところ、 男子の平均点が$x$点で、
女子の平均点が$y$点であった。このクラスのテストの合計点は何点か、
$y$を使った式で表しなさい。
⑩三角柱と三角すいがあり、底面は相似な三角形で高さが等しい。
三角柱の底面と三角すいの底面の相似比が$1:2$であるとき、
三角柱の体積は三角すいの体積の何倍か、求めなさい。
この動画を見る
①$(- 4) + 3\times (- 3)$を計算しなさい。
②$\dfrac{2x - 1}{3} - \dfrac{3x + 1}{5}$を計算しなさい。
③$(\sqrt{12} + \sqrt{18})(\sqrt3 - \sqrt2)$を計算しなさい。
④$(x - 4)^ 2 + 2(x - 2) - 3$を因数分解しなさい。
⑤方程式$(x + 3)(x - 5) = 5x - 24$を解きなさい。
⑥次の連立方程式を解きなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
4x+5=3y-2 \\
3x+2y=16
\end{array}
\right.
\end{eqnarray}$
⑦関数$y=-3x^2$について、
$x$の値が1から3まで増加するときの変化の割合を求めなさい。
⑧1つのさいころを2回投げるとき、1回目に出た目の数が、
2回目に出た目の数の倍数となる確率を求めなさい。
⑨男子20人、好16人のクラスでテストを行ったところ、 男子の平均点が$x$点で、
女子の平均点が$y$点であった。このクラスのテストの合計点は何点か、
$y$を使った式で表しなさい。
⑩三角柱と三角すいがあり、底面は相似な三角形で高さが等しい。
三角柱の底面と三角すいの底面の相似比が$1:2$であるとき、
三角柱の体積は三角すいの体積の何倍か、求めなさい。
【高校受験対策】数学-図形18

単元:
#数学(中学生)#中1数学#中2数学#中3数学#円#平面図形#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①右の図1のような$\triangle ABC$があります。
点$D、E$はそれぞれ辺$AB、BC$上の点で、$\angle BDE =\angle ACB$です。
$AD = 2cm 、 DB = 8cm 、 BE = 6cm$のとき、$EC$の長さを求めなさい。
② 右の図2は、正方形$ABCD$と、おうぎ形$BAC$、おうぎ形$CBD$を組み合わせたものです。
点$E$は$\stackrel{\huge\frown}{AC}$と$\stackrel{\huge\frown}{BD}$との交点です。
正方形$ABCD$の1辺の長さが$12cm$のとき、$\stackrel{\huge\frown}{BE}$の長さを求めなさい。 ただし、円周率は$\pi$とします。
③右の図3のような四角形$ABCD$があり、対角線$AC$と対角線$BD$との交点を$E$とする。
線分$BE$上に、2点$B、E$と異なる点$F$をとり、直線$AF$と辺$BC$との交点を$G$とする。
四角形$ABCD$の面積が$50cm²$、$△AGC$の面積が$30cm$、
$BF:FD=3:4、AF:FG=2:1$であるとき、$△ACD$の面積は何$cm^2$か。
図は動画内参照
この動画を見る
①右の図1のような$\triangle ABC$があります。
点$D、E$はそれぞれ辺$AB、BC$上の点で、$\angle BDE =\angle ACB$です。
$AD = 2cm 、 DB = 8cm 、 BE = 6cm$のとき、$EC$の長さを求めなさい。
② 右の図2は、正方形$ABCD$と、おうぎ形$BAC$、おうぎ形$CBD$を組み合わせたものです。
点$E$は$\stackrel{\huge\frown}{AC}$と$\stackrel{\huge\frown}{BD}$との交点です。
正方形$ABCD$の1辺の長さが$12cm$のとき、$\stackrel{\huge\frown}{BE}$の長さを求めなさい。 ただし、円周率は$\pi$とします。
③右の図3のような四角形$ABCD$があり、対角線$AC$と対角線$BD$との交点を$E$とする。
線分$BE$上に、2点$B、E$と異なる点$F$をとり、直線$AF$と辺$BC$との交点を$G$とする。
四角形$ABCD$の面積が$50cm²$、$△AGC$の面積が$30cm$、
$BF:FD=3:4、AF:FG=2:1$であるとき、$△ACD$の面積は何$cm^2$か。
図は動画内参照
【高校受験対策】数学-死守27

単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#平方根#2次方程式#比例・反比例#空間図形#円#表とグラフ#表とグラフ・集合
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$x-6x$を計算しなさい。
②$\sqrt{28)}- \sqrt{7}$を計算しなさい。
③$x = sqrt2 + 3$のとき、$x ^ 2 - 6x + 9$の値を求めなさい。
④2次方程式$x ^ 2 - 2x - 7 = 0$を解きなさい。
⑤次の連立方程式を解きなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+3y=4 \\
3x+2y=19
\end{array}
\right.
\end{eqnarray}$
⑥$y$は$x$に反比例し、$x = - 4a$のとき、$y = 3$です。
$x = 2$のときの$y$の値を求めなさい。
⑦中学生12人が、あるゲームを行いました。
左下の資料1は、そのゲームの得点を示したものです。
この資料の中央値(メジアン)と分布の範囲をそれぞれ求めなさい。
⑧半径が8cm、弧の長さが4匹cmのおうぎ形の面積を求めなさい。
ただし、円周率は$\pi$とする。
⑨ある2けたの自然数は、十の位の数と一の位の数の和が10で、
十の位の数と一の位の数の積が21です。
この2けたの自然数として考えられる数をすべて求めなさい。
⑩右の図のような三角柱$ABC-DEF$があります。
点$G$は辺$AD$の中点です。
三角柱$ABC-DEF$の体積は三角錐$G-DEF$の体積の何倍ですか。
図は動画内参照
この動画を見る
①$x-6x$を計算しなさい。
②$\sqrt{28)}- \sqrt{7}$を計算しなさい。
③$x = sqrt2 + 3$のとき、$x ^ 2 - 6x + 9$の値を求めなさい。
④2次方程式$x ^ 2 - 2x - 7 = 0$を解きなさい。
⑤次の連立方程式を解きなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+3y=4 \\
3x+2y=19
\end{array}
\right.
\end{eqnarray}$
⑥$y$は$x$に反比例し、$x = - 4a$のとき、$y = 3$です。
$x = 2$のときの$y$の値を求めなさい。
⑦中学生12人が、あるゲームを行いました。
左下の資料1は、そのゲームの得点を示したものです。
この資料の中央値(メジアン)と分布の範囲をそれぞれ求めなさい。
⑧半径が8cm、弧の長さが4匹cmのおうぎ形の面積を求めなさい。
ただし、円周率は$\pi$とする。
⑨ある2けたの自然数は、十の位の数と一の位の数の和が10で、
十の位の数と一の位の数の積が21です。
この2けたの自然数として考えられる数をすべて求めなさい。
⑩右の図のような三角柱$ABC-DEF$があります。
点$G$は辺$AD$の中点です。
三角柱$ABC-DEF$の体積は三角錐$G-DEF$の体積の何倍ですか。
図は動画内参照
【高校受験対策】関数-30

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図で、曲線は関数$y = \dfrac{1}{2}x^2$のグラフです。
2点$A、B$は曲線上の点で、点$A$の座標は(-4,8)、点$B$の座標は(2,2)です。
曲線上の$x \lt 0$の部分に点C、曲線上の$x \gt 0$の部分に点Dを、
$CD//AB$となるようにとり、線分 $CD$と$y$軸との交点を$E$とします。
このとき、次の各問に答えなさい。
①2点$A、B$を通る直線の式を求めなさい。
②関数$y=\dfrac{1}{2}x^2$で、$x$の変域が$-4 \leqq x \leqq 2$のとき、
その変域を求めなさい。
③$△ACE$と$△BDE$の面積の比が8:5のとき、点$c$の$x$座標を求めなさい。
図は動画内参照
この動画を見る
右の図で、曲線は関数$y = \dfrac{1}{2}x^2$のグラフです。
2点$A、B$は曲線上の点で、点$A$の座標は(-4,8)、点$B$の座標は(2,2)です。
曲線上の$x \lt 0$の部分に点C、曲線上の$x \gt 0$の部分に点Dを、
$CD//AB$となるようにとり、線分 $CD$と$y$軸との交点を$E$とします。
このとき、次の各問に答えなさい。
①2点$A、B$を通る直線の式を求めなさい。
②関数$y=\dfrac{1}{2}x^2$で、$x$の変域が$-4 \leqq x \leqq 2$のとき、
その変域を求めなさい。
③$△ACE$と$△BDE$の面積の比が8:5のとき、点$c$の$x$座標を求めなさい。
図は動画内参照
【テスト対策 中1】6章-8

単元:
#数学(中学生)#中1数学#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の図形を辺$AD$を軸として1回転させてできる
立体の体積と表面積を求めなさい。
図は動画内参照
この動画を見る
◎次の図形を辺$AD$を軸として1回転させてできる
立体の体積と表面積を求めなさい。
図は動画内参照
【テスト対策 中1】6章-7

単元:
#数学(中学生)#中1数学#空間図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①図1のような1辺の長さが3cmの立方体がある。
この立方体を平面$DEG$で切ってできる三角錐の体積を求めなさい。
②図2は、$A$は底面の半径が4cm、深さが9cmの円錐の容器、
$B$は底面の半径が 2cmの円柱の容器である。
満水にした容器$A$の水を容器$B$に移したところ、
容器$B$の深さの$\dfrac{3}{5}$まで水がはいった。
容器$B$の深さは何cmか求めなさい。
図は動画内参照
この動画を見る
①図1のような1辺の長さが3cmの立方体がある。
この立方体を平面$DEG$で切ってできる三角錐の体積を求めなさい。
②図2は、$A$は底面の半径が4cm、深さが9cmの円錐の容器、
$B$は底面の半径が 2cmの円柱の容器である。
満水にした容器$A$の水を容器$B$に移したところ、
容器$B$の深さの$\dfrac{3}{5}$まで水がはいった。
容器$B$の深さは何cmか求めなさい。
図は動画内参照
【テスト対策 中1】6章-6

単元:
#数学(中学生)#中1数学#空間図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①図1のように、底面の半径が4cmの円錐を、頂点を固定して転がしたところ、
ちょうど3回転してもとの位置にもどった。
このとき、この円錐の側面積を求めなさい。
②図2の図形を、直線$\ell$を軸として
1回転したときにできる立体の表面積と体積をそれぞれ求めなさい。
図は動画内参照
この動画を見る
①図1のように、底面の半径が4cmの円錐を、頂点を固定して転がしたところ、
ちょうど3回転してもとの位置にもどった。
このとき、この円錐の側面積を求めなさい。
②図2の図形を、直線$\ell$を軸として
1回転したときにできる立体の表面積と体積をそれぞれ求めなさい。
図は動画内参照
【テスト対策 中1】6章-5

単元:
#数学(中学生)#中1数学#空間図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①図1の円錐の展開図で、底面の円$O$の半径を求めなさい。
②図2は、立方体の展開図である。これを組み立てて立方体をつくるとき、
辺$AB$に平行な面をア~カからすべて選びなさい。
図は動画内参照
この動画を見る
①図1の円錐の展開図で、底面の円$O$の半径を求めなさい。
②図2は、立方体の展開図である。これを組み立てて立方体をつくるとき、
辺$AB$に平行な面をア~カからすべて選びなさい。
図は動画内参照
【テスト対策 中1】6章-4
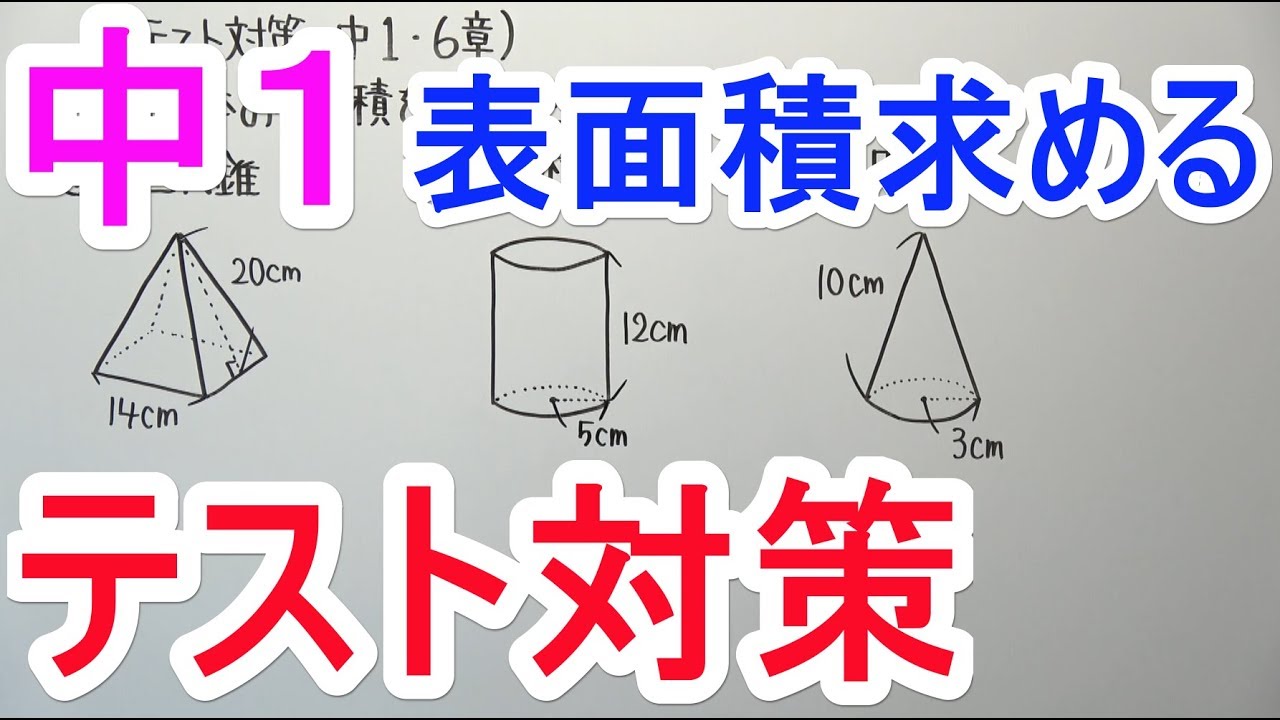
単元:
#数学(中学生)#中1数学#空間図形#立体図形#立体切断
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の立体の表面積を求めなさい。
①正四角錐
②円柱
③円錐
この動画を見る
◎次の立体の表面積を求めなさい。
①正四角錐
②円柱
③円錐
【テスト対策 中1】6章-3

単元:
#数学(中学生)#中1数学#空間図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①図1の直方体において、辺$BF$とねじれの位置にある辺をすべて書きなさい。
図2のように、$AB//DC$の台形$ABCD$を底面とする四角柱がある。
このとき、辺$AB$と次の関係にある辺をすべて書きなさい。
②平行な辺
③垂直な辺
④ねじれの位置にある辺
図は動画内参照
この動画を見る
①図1の直方体において、辺$BF$とねじれの位置にある辺をすべて書きなさい。
図2のように、$AB//DC$の台形$ABCD$を底面とする四角柱がある。
このとき、辺$AB$と次の関係にある辺をすべて書きなさい。
②平行な辺
③垂直な辺
④ねじれの位置にある辺
図は動画内参照
【テスト対策 中1】6章-2
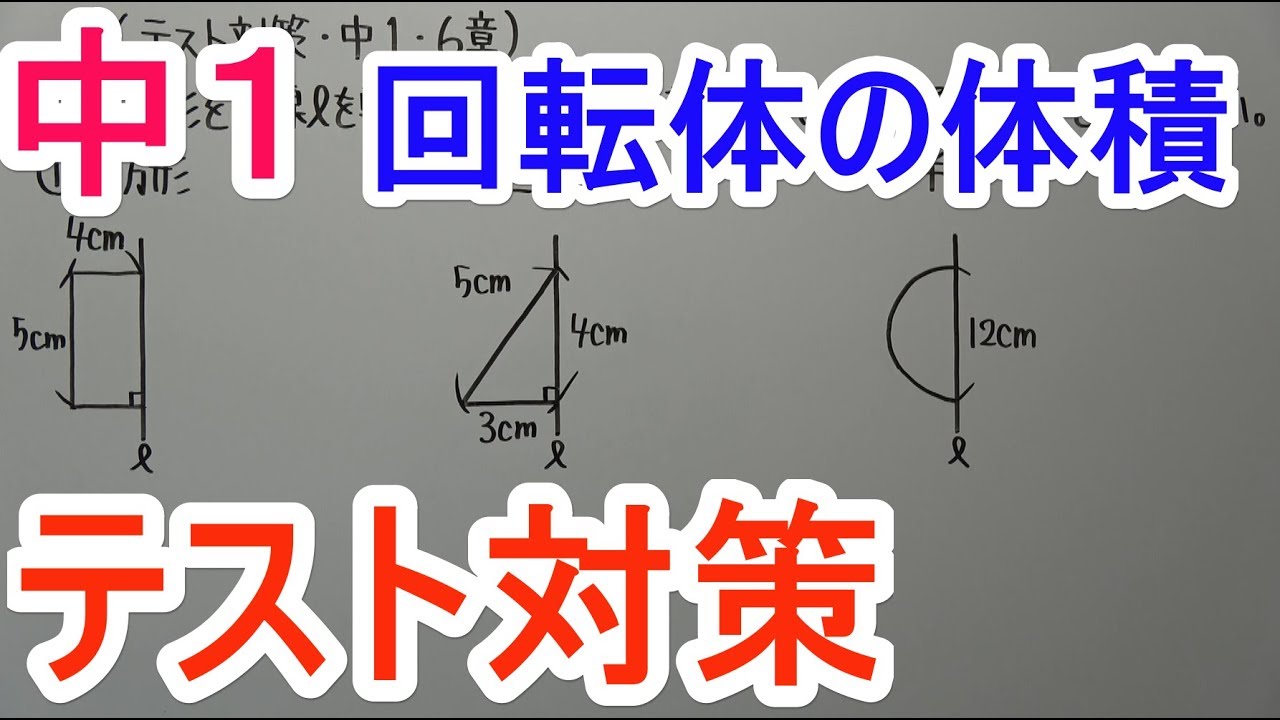
単元:
#数学(中学生)#中1数学#空間図形#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の図形を直線を軸として1回転してできる立体の名前とその体積を求めなさい。
①長方形
②三角形
③半円
図は動画内参照
この動画を見る
◎次の図形を直線を軸として1回転してできる立体の名前とその体積を求めなさい。
①長方形
②三角形
③半円
図は動画内参照
【テスト対策 中1】6章-1

単元:
#数学(中学生)#中1数学#平行と合同#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次のことがらのうち、つねに成り立つものをすべて選びなさい。
ただし、$\ell、m、n$は直線、$A、B、C$は平面とする。
①$ℓ//m、m\perp n$ならば$\ell \perp n$
②$ℓ//m、m//n$ならば$ℓ//n$
③$\ell \perp m、m\perp n$ならば$\ell //n$
④$ℓ//A、m//A$ならば$ℓ//m$
⑤$\ell \perp A、m\perp A$ならば$ℓ//m$
⑥$A//C、B//C$ならば$A//B$
⑦$A\perp C、B\perp C$ならば$A//B$
⑧$A//B、\ell \perp A$ならば$\ell \perp B$
この動画を見る
◎次のことがらのうち、つねに成り立つものをすべて選びなさい。
ただし、$\ell、m、n$は直線、$A、B、C$は平面とする。
①$ℓ//m、m\perp n$ならば$\ell \perp n$
②$ℓ//m、m//n$ならば$ℓ//n$
③$\ell \perp m、m\perp n$ならば$\ell //n$
④$ℓ//A、m//A$ならば$ℓ//m$
⑤$\ell \perp A、m\perp A$ならば$ℓ//m$
⑥$A//C、B//C$ならば$A//B$
⑦$A\perp C、B\perp C$ならば$A//B$
⑧$A//B、\ell \perp A$ならば$\ell \perp B$
【テスト対策 中3】6章-5
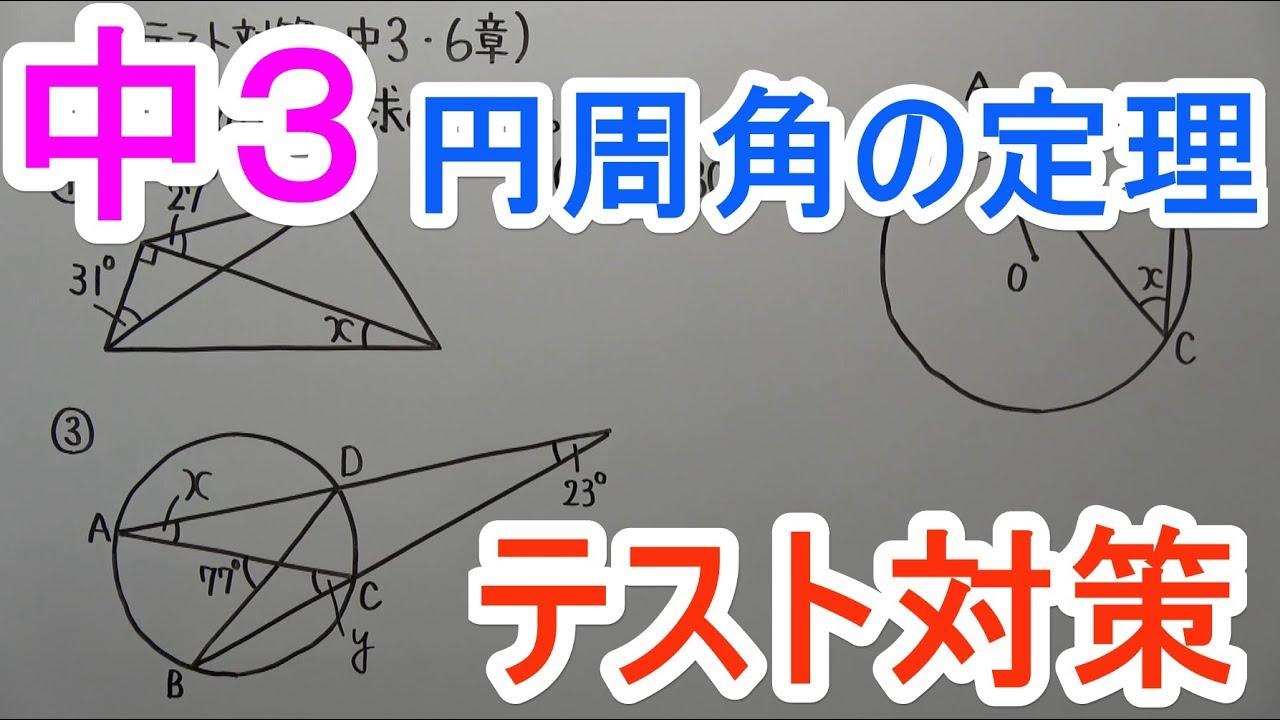
単元:
#数学(中学生)#中2数学#中3数学#円#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$\angle x,\angle y$の大きさを求めなさい。
図①~③は動画内参照
この動画を見る
$\angle x,\angle y$の大きさを求めなさい。
図①~③は動画内参照
【テスト対策 中3】6章-4

単元:
#数学(中学生)#中3数学#円
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①下の図1は線分$AF$を直径とする半円$O$で、
点$B~E$は弧$AF$を5等分する点である。
このとき、$\angle x$の大きさを求めなさい。
②下の図2で、点$A~F$は円周上の6等分点である。
このとき、$\angle x$の大きさを求めなさい。
図は動画内参照
この動画を見る
①下の図1は線分$AF$を直径とする半円$O$で、
点$B~E$は弧$AF$を5等分する点である。
このとき、$\angle x$の大きさを求めなさい。
②下の図2で、点$A~F$は円周上の6等分点である。
このとき、$\angle x$の大きさを求めなさい。
図は動画内参照
【テスト対策 中3】6章-3
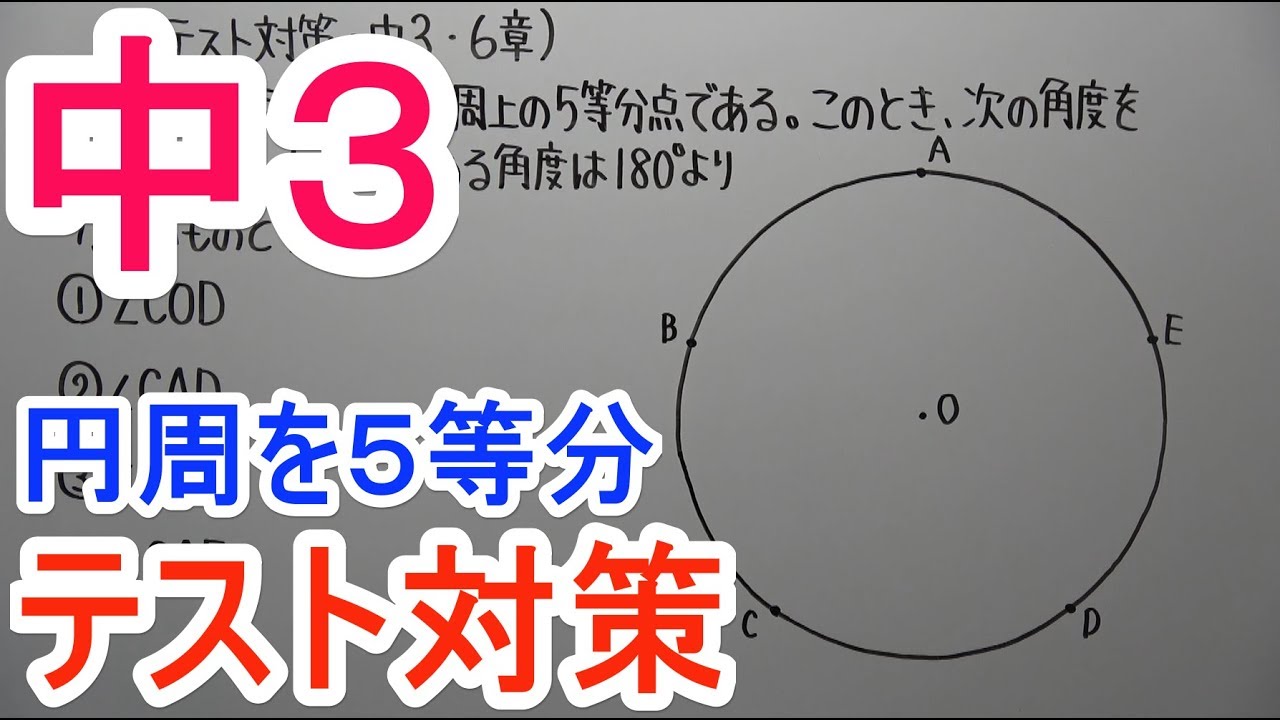
単元:
#数学(中学生)#中3数学#円
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎右の図で、点$A~E$は円周上の5等分点である。
このとき、次の角度を求めなさい。
ただし、求める角度は$180°$より小さいものとする。
①$\angle COD$
②$\angle CAD$
③$\angle BOD$
④$\angle CAE$
図は動画内参照
この動画を見る
◎右の図で、点$A~E$は円周上の5等分点である。
このとき、次の角度を求めなさい。
ただし、求める角度は$180°$より小さいものとする。
①$\angle COD$
②$\angle CAD$
③$\angle BOD$
④$\angle CAE$
図は動画内参照
【テスト対策 中3】6章-2
単元:
#数学(中学生)#中3数学#円
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
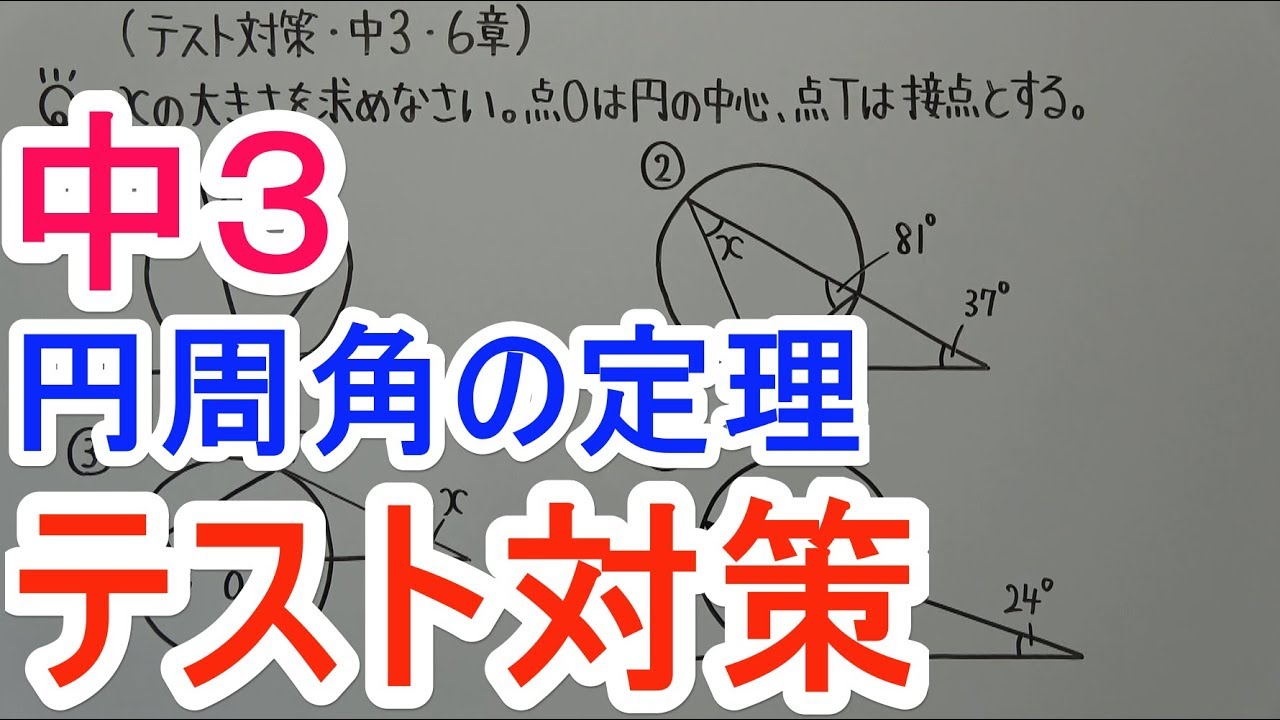
$\angle x$の大きさを求めなさい。点$O$は円の中心、点$T$は接点とする。
図①~④は動画内参照
この動画を見る
$\angle x$の大きさを求めなさい。点$O$は円の中心、点$T$は接点とする。
図①~④は動画内参照
【テスト対策 中3】6章-1

単元:
#数学(中学生)#中3数学#円
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$\angle x$の大きさを求めなさい。点$O$は円の中心とする。
図①~⑤は動画内参照
この動画を見る
$\angle x$の大きさを求めなさい。点$O$は円の中心とする。
図①~⑤は動画内参照
【テスト対策 中1】5章-6

【テスト対策 中1】5章-5

単元:
#数学(中学生)#中1数学#空間図形#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①半径$8cm$、弧の長さ$6\pi cm$のおうぎ形の中心角の大きさと面積を求めなさい。
②中心角72、弧の長さ$4\pi cm$のおうぎ形の半径を求めなさい。
③半径15cmのおうぎ形で、弧の長さが半径6cmの円の周に等しいとき、
このおうぎ形の中心角の大きさを求めなさい。
図は動画内参照
この動画を見る
①半径$8cm$、弧の長さ$6\pi cm$のおうぎ形の中心角の大きさと面積を求めなさい。
②中心角72、弧の長さ$4\pi cm$のおうぎ形の半径を求めなさい。
③半径15cmのおうぎ形で、弧の長さが半径6cmの円の周に等しいとき、
このおうぎ形の中心角の大きさを求めなさい。
図は動画内参照
【テスト対策 中1】5章-4
単元:
#数学(中学生)#円
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
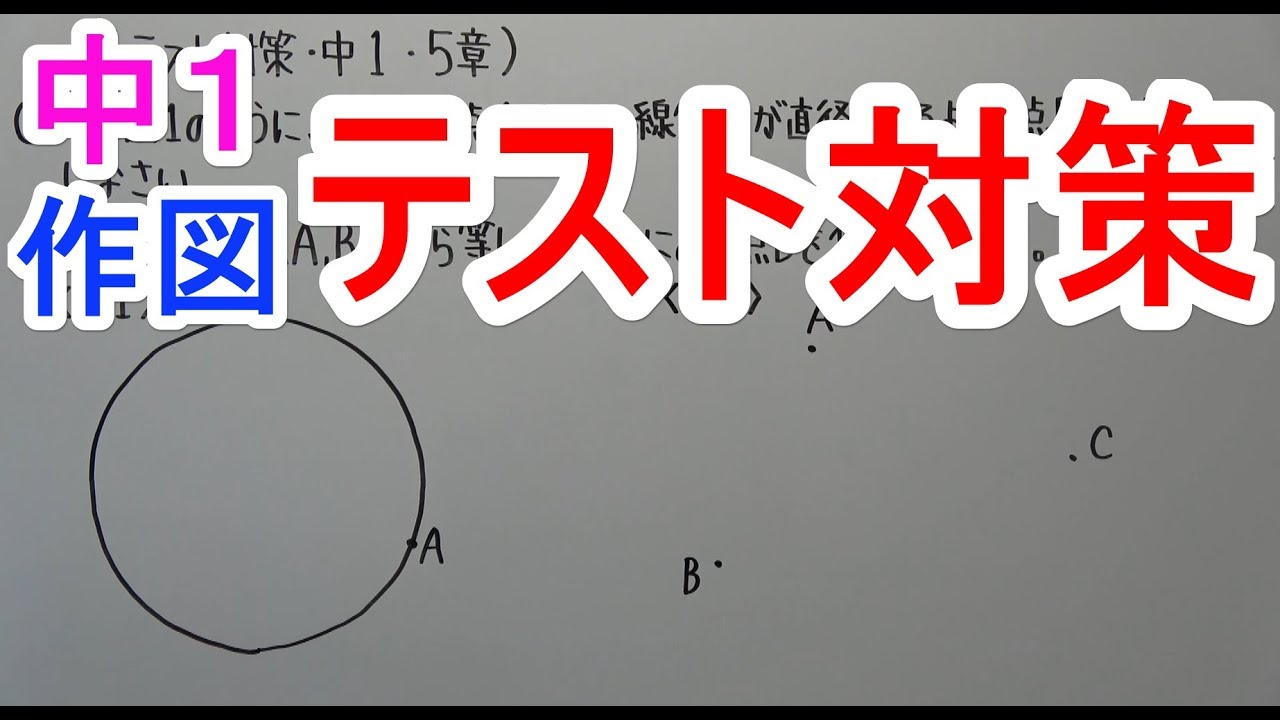
①下の図1のように、円周上に点$A$がある。
線分$AB$が直径となるように点$B$を作図しなさい。
②下の図2の3点$A、B、C$から等しい距離にある点$D$を作図しなさい。
図は動画内参照
この動画を見る
①下の図1のように、円周上に点$A$がある。
線分$AB$が直径となるように点$B$を作図しなさい。
②下の図2の3点$A、B、C$から等しい距離にある点$D$を作図しなさい。
図は動画内参照
【テスト対策 中1】5章-2

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
◎次の$\Box$にあてはまることばを書きなさい。
・平面上で、図形をある点$O$を中心にして一定の角度だけまわすことを$\Box$といい、
点$O$を$\Box$という。
その中で、180℃の$\Box$を$\Box$という。
・平面上で、図形をある直線$\ell$を折り目として折り返すことを$\Box$といい、
直線$\ell$を$\Box$という。
$\Box$で移りあう図形は、$\Box$について$\Box$対で、
対応する点を結んだ線分は$\Box$と$\Box$に交わり、
その交点で$\Box$される。
この動画を見る
◎次の$\Box$にあてはまることばを書きなさい。
・平面上で、図形をある点$O$を中心にして一定の角度だけまわすことを$\Box$といい、
点$O$を$\Box$という。
その中で、180℃の$\Box$を$\Box$という。
・平面上で、図形をある直線$\ell$を折り目として折り返すことを$\Box$といい、
直線$\ell$を$\Box$という。
$\Box$で移りあう図形は、$\Box$について$\Box$対で、
対応する点を結んだ線分は$\Box$と$\Box$に交わり、
その交点で$\Box$される。
【テスト対策 中1】5章-1

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の$\Box$にあてはまることばや記号を書きなさい。
・2直線$AB、CD$が交わってできる角が直角のとき、
$AB$と$CD$は$\Box$であるといい、 ②$AB\Box CD$と表す。
また、2直線$\ell、m$が交わらないとき、$\ell$は$m$はといい、$AB \Box CD$と表す。
・図形の形と大きさを変えないで、位置だけを変えることを$\Box$という。
・平面上で、図形を一定の方向に、一定の長さだけずらすことを$\Box$といい、
このとき、対応する2点を結ぶ線分は、それぞれ$\Box$で長さが$\Box$。
この動画を見る
次の$\Box$にあてはまることばや記号を書きなさい。
・2直線$AB、CD$が交わってできる角が直角のとき、
$AB$と$CD$は$\Box$であるといい、 ②$AB\Box CD$と表す。
また、2直線$\ell、m$が交わらないとき、$\ell$は$m$はといい、$AB \Box CD$と表す。
・図形の形と大きさを変えないで、位置だけを変えることを$\Box$という。
・平面上で、図形を一定の方向に、一定の長さだけずらすことを$\Box$といい、
このとき、対応する2点を結ぶ線分は、それぞれ$\Box$で長さが$\Box$。
【テスト対策 中2】5章-6

単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①右の図のように、正三角形$ABC$において辺$AC$上に点$D$をとり、
$AE//BC$、$AD=AE$となるように点$E$をとる。
このとき、$BD=CE$であることを証明しなさい。
図は動画内参照
この動画を見る
①右の図のように、正三角形$ABC$において辺$AC$上に点$D$をとり、
$AE//BC$、$AD=AE$となるように点$E$をとる。
このとき、$BD=CE$であることを証明しなさい。
図は動画内参照
【テスト対策 中2】5章-5
単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
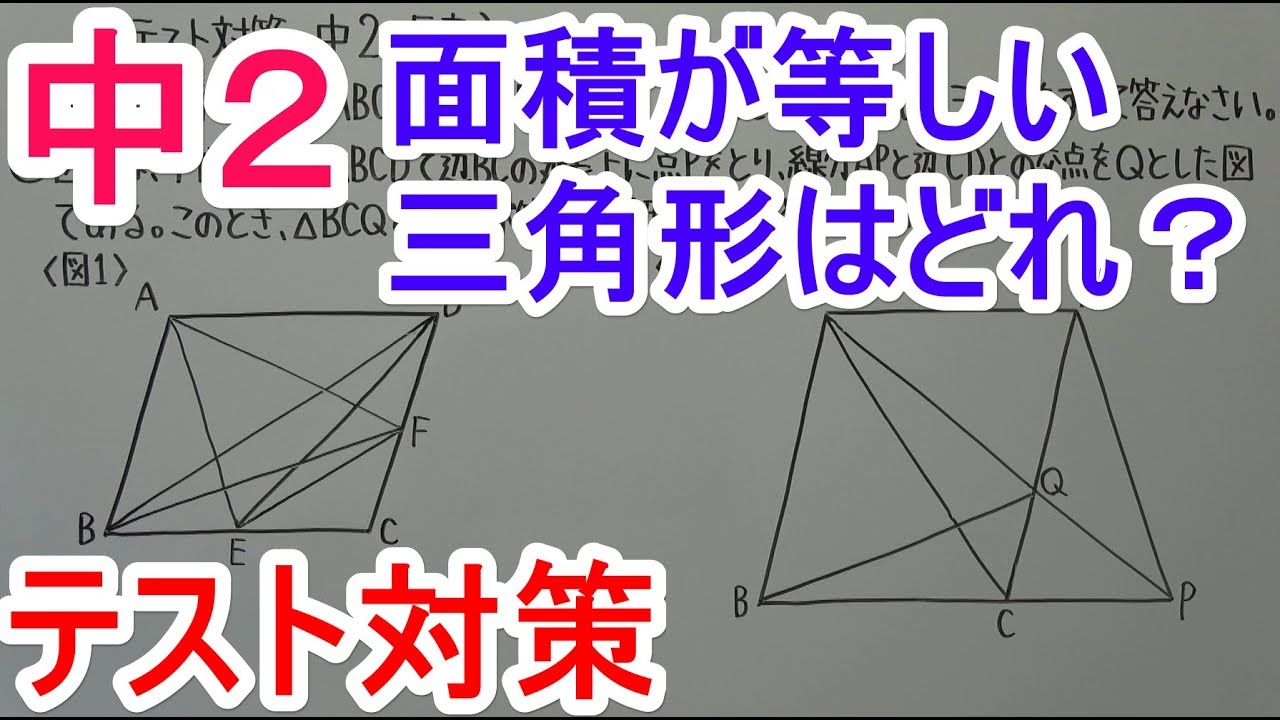
①図1は、平行四辺形$ABCD$で$BD//EF$である。
$△ABE$と面積が等しい三角形をすべて答えなさい。
②図2は、平行四辺形$ABCD$で辺$BC$の延長上に点$P$をとり、
線分$AP$と辺$CD$との交点を$Q$とした図である。
このとき、$△BCQ$と面積が等しい三角形をすべて答えなさい。
図は動画内参照
この動画を見る
①図1は、平行四辺形$ABCD$で$BD//EF$である。
$△ABE$と面積が等しい三角形をすべて答えなさい。
②図2は、平行四辺形$ABCD$で辺$BC$の延長上に点$P$をとり、
線分$AP$と辺$CD$との交点を$Q$とした図である。
このとき、$△BCQ$と面積が等しい三角形をすべて答えなさい。
図は動画内参照
【テスト対策 中2】5章-4
単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
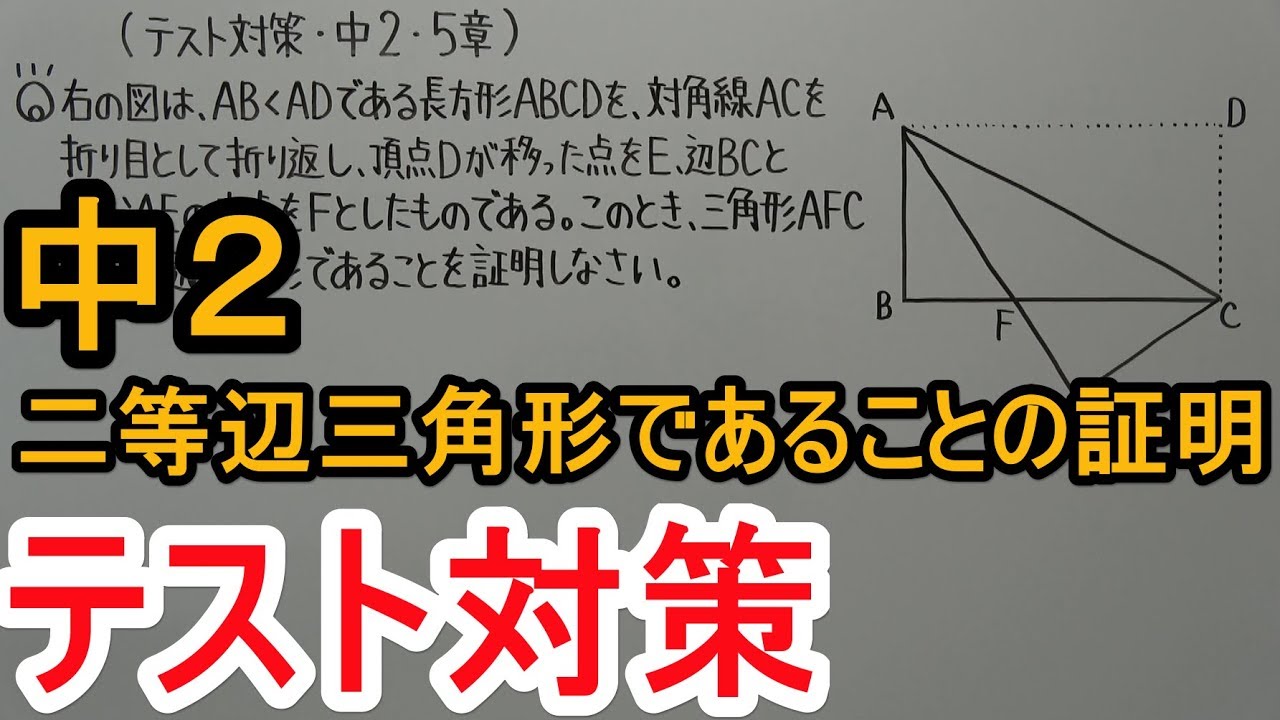
右の図は、$AB\lt AD$である長方形$ABCD$を、
対角線$AC$を折り目として折り返し、頂点$D$が移った点を$E$、
辺$BC$と線分$AE$の交点を$F$としたものである。
このとき、三角形$AFC$は二等辺三角形であることを証明しなさい。
図は動画内参照
この動画を見る
右の図は、$AB\lt AD$である長方形$ABCD$を、
対角線$AC$を折り目として折り返し、頂点$D$が移った点を$E$、
辺$BC$と線分$AE$の交点を$F$としたものである。
このとき、三角形$AFC$は二等辺三角形であることを証明しなさい。
図は動画内参照
【テスト対策 中2】5章-3
単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
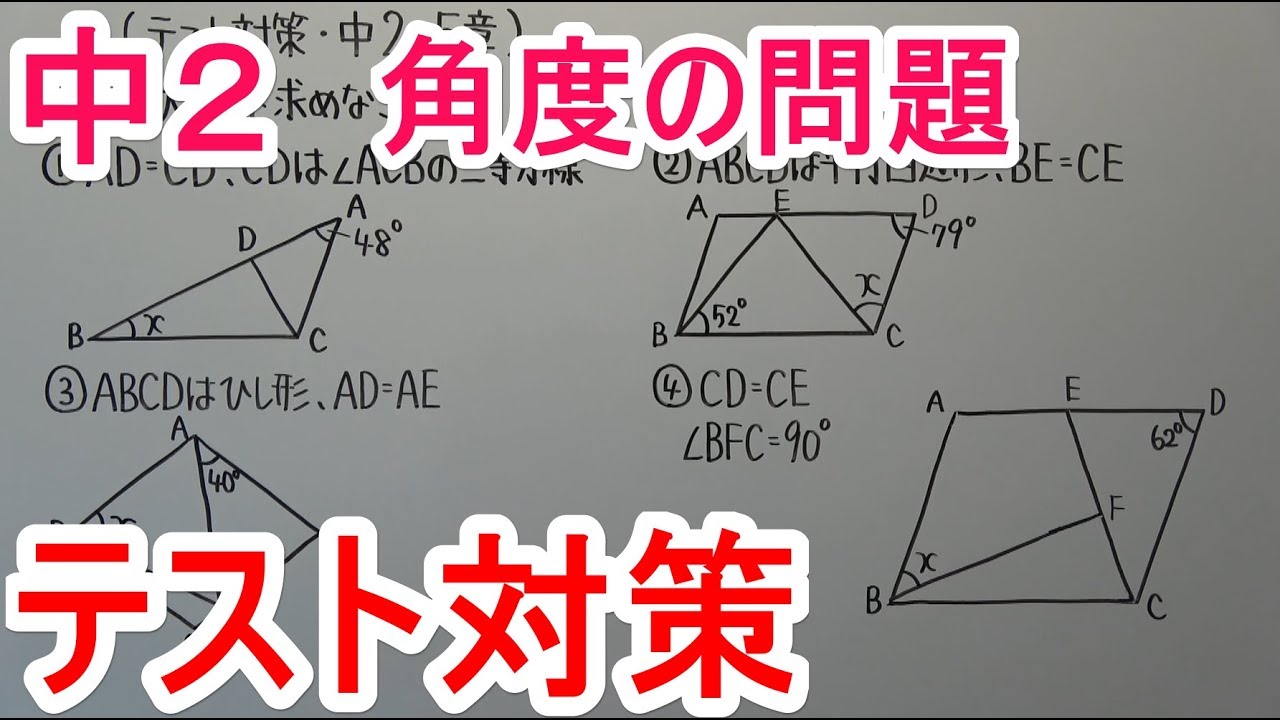
$\angle x$の大きさを求めなさい。
①$AD=CD,CD$は$\angle ACB$の二等分線
②$ABCD$は平行四辺形、$BE=CE$
③$ABCD$はひし形、$AD=AE$
④$CD=CE$
$BFC=90°$
図は動画内参照
この動画を見る
$\angle x$の大きさを求めなさい。
①$AD=CD,CD$は$\angle ACB$の二等分線
②$ABCD$は平行四辺形、$BE=CE$
③$ABCD$はひし形、$AD=AE$
④$CD=CE$
$BFC=90°$
図は動画内参照
【テスト対策 中2】5章-2

単元:
#数学(中学生)#中2数学#平行と合同
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図において、$AB=CD,AB /\!/ CD$のとき、
$AO=CO$であることを証明しなさい。
図は動画内参照
この動画を見る
右の図において、$AB=CD,AB /\!/ CD$のとき、
$AO=CO$であることを証明しなさい。
図は動画内参照
【テスト対策 中2】5章-1
単元:
#数学(中学生)#中2数学#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
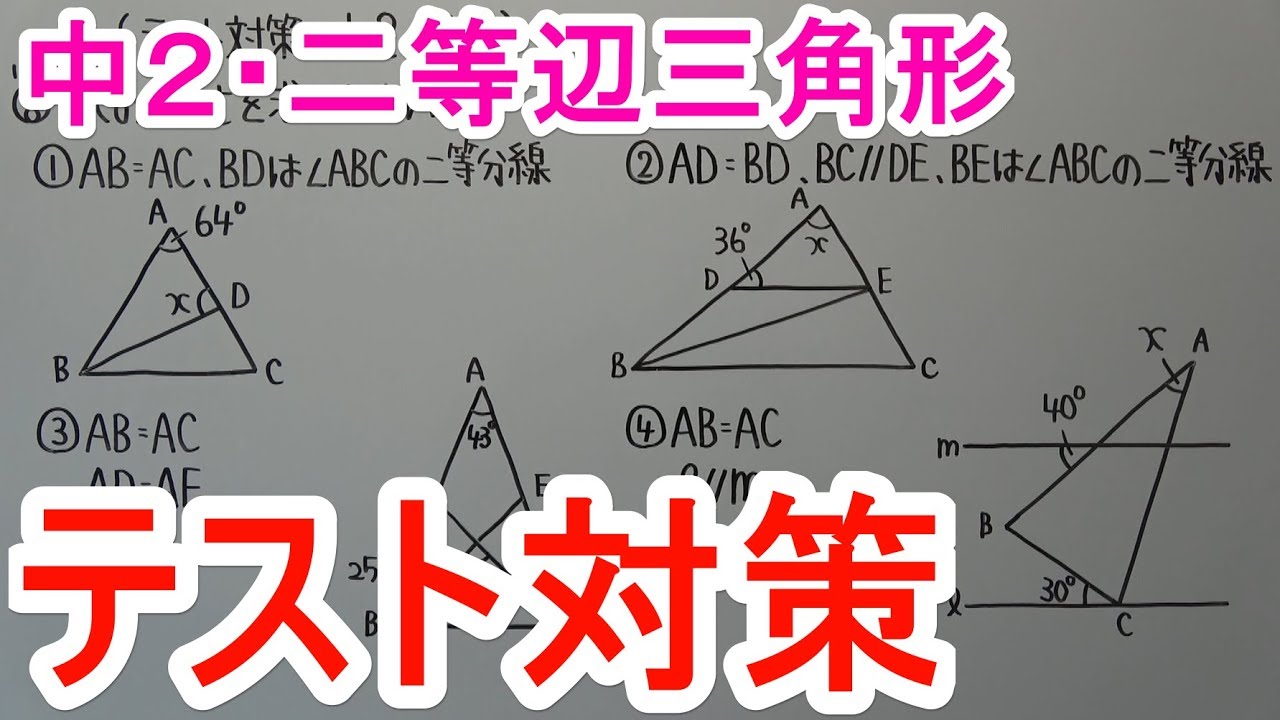
$\angle x$の大きさを求めなさい。
①$AB=AC,BD$は$\angle ABC$の二等分線
②$AD=BD,BC /\!/ DE,BE$は$\angle ABC$の二等分線
③$AB=AC$
$AD=AE$
④$AB=AC$
$\ell /\!/ m$
図は動画内参照
この動画を見る
$\angle x$の大きさを求めなさい。
①$AB=AC,BD$は$\angle ABC$の二等分線
②$AD=BD,BC /\!/ DE,BE$は$\angle ABC$の二等分線
③$AB=AC$
$AD=AE$
④$AB=AC$
$\ell /\!/ m$
図は動画内参照
【テスト対策 中3】5章-8

単元:
#数学(中学生)#中3数学#相似な図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
右の図のように、平行四辺形$ABCD$の辺$BC、CD$上にそれぞれ点$E、F$をとり、
$BE:EC =2 :1、CF:FD=2:1$とする。
直線$AE、AF$と対角線$BD$との交点をそれぞれ$P、Q$とする。
また、平行四辺形$ABCD$の面積を$S$とする。
①$AD: BE$を求めなさい。
②$AQ:QF$を求めなさい。
③$△PBE$の面積を$S$で表しなさい。
④$△AQD$の面積を$S$で表しなさい。
図は動画内参照
この動画を見る
右の図のように、平行四辺形$ABCD$の辺$BC、CD$上にそれぞれ点$E、F$をとり、
$BE:EC =2 :1、CF:FD=2:1$とする。
直線$AE、AF$と対角線$BD$との交点をそれぞれ$P、Q$とする。
また、平行四辺形$ABCD$の面積を$S$とする。
①$AD: BE$を求めなさい。
②$AQ:QF$を求めなさい。
③$△PBE$の面積を$S$で表しなさい。
④$△AQD$の面積を$S$で表しなさい。
図は動画内参照
【テスト対策 中3】5章-7

単元:
#数学(中学生)#中3数学#相似な図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①右の図1で、四角形$ABCD$は$AD/\!/ BC、 \angle ABC = 90°$の台形で、
$E$は線分$AC$と$DB$との交点である。
$AB=BC=6cm、 AD=3cm$のとき、$△BCE$の面積を求めなさい。
② 右の図2において、$AB=5cm、BC=4cm、CD=2cm、\angle ABC= \angle BCD = 90°$である。
このとき、$△BCE$の面積を求めなさい。
図は動画内参照
この動画を見る
①右の図1で、四角形$ABCD$は$AD/\!/ BC、 \angle ABC = 90°$の台形で、
$E$は線分$AC$と$DB$との交点である。
$AB=BC=6cm、 AD=3cm$のとき、$△BCE$の面積を求めなさい。
② 右の図2において、$AB=5cm、BC=4cm、CD=2cm、\angle ABC= \angle BCD = 90°$である。
このとき、$△BCE$の面積を求めなさい。
図は動画内参照
